1.2.2 数轴 同步课件(共20张PPT) 2023-2024学年七年级数学上册人教版
文档属性
| 名称 | 1.2.2 数轴 同步课件(共20张PPT) 2023-2024学年七年级数学上册人教版 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-17 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
人教版数学七年级上册——第一章
《有理数》
1.2.2数轴
05
06
课堂小结
07
教学目标
01
学习任务
02
数轴的认识
03
新课导入
04
课后作业
有理数与数轴上的点的关系
1.能判断一个数是正数还是负数,能用正数或负数表示生活中具有相反意义的量.
2.借助生活中的实例理解有理数的意义,体会负数引入的必要性和有理 数应用的广泛性.
3.培养学生主动探索,积极思考的学习兴趣培养学生积极思考,合作交流的意识和能 力.
教学目的
了解数值的概念,会使用数轴上的点表示有理数.
掌握数轴三要素和有理数集中,原点和数的符号之间的对应关系。
学习任务
1.认识数轴
2.数轴上的点与有理数的关系
新课导入
在一条东西向的马路上,有一个汽车站牌,汽车站牌东3m和7.5m处有一棵柳树和一棵杨树,汽车站西3m和4.8m处分别有一棵槐树和一根电线杆,试画图表示这一情境.
杨树
槐树
柳树
电线杆
汽车站牌
0
东3m
东7.5m
3
7.5
西3m
3
西4.8m
4.8
新课导入
怎样简明地表示这些树、电线杆与汽车站牌的相对位置关系(方向、距离)?
杨树
槐树
柳树
电线杆
汽车站牌
0
东3m
东7.5m
3
7.5
西3m
3
西4.8m
4.8
数轴的认识
为了使表达更清楚,我们规定向东为正,把汽车站牌左右两边的位置对应的距离分别用负数和正数表示.
0
3
7.5
-3
-4.8
把正数、0和负数用一条直线上的点表示出来.
圆周率π是正数,但不是有理数,千万要注意,类似,-等同样也不是有理数.
数轴的认识
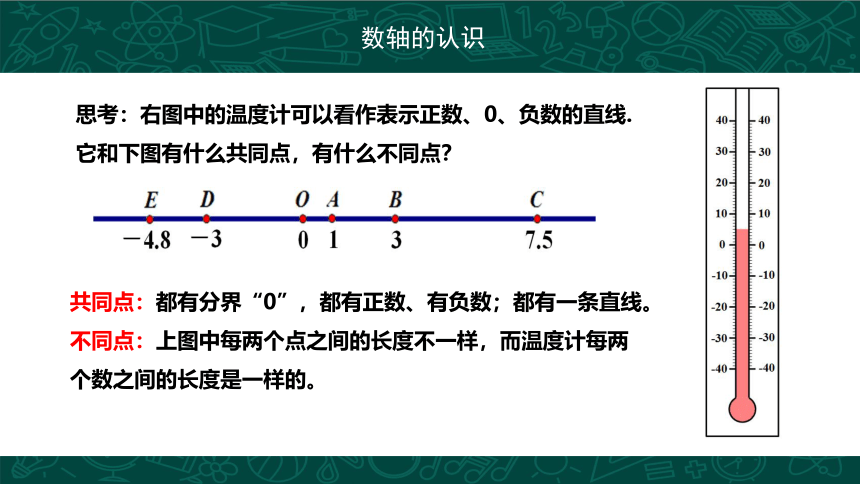
思考:右图中的温度计可以看作表示正数、0、负数的直线.
它和下图有什么共同点,有什么不同点?
共同点:都有分界“0”,都有正数、有负数;都有一条直线。
不同点:上图中每两个点之间的长度不一样,而温度计每两个数之间的长度是一样的。
圆周率π是正数,但不是有理数,千万要注意,类似,-等同样也不是有理数.
数轴的认识
在数学上可以用一条直线上的点表示数,这条直线叫做数轴。那什么是数轴呢?
定义:规定了原点、正方向、单位长度的直线叫做数轴。
圆周率π是正数,但不是有理数,千万要注意,类似,-等同样也不是有理数.
数轴的认识
注意:
(1)在直线上任取一点表示数0,这个点叫做原点;
(2)通常规定直线上从原点向右(或上)为正方向,从原点向左(或下)为负方向
(3)选取适当的长度为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表示你1,2,3…;从原点向左,用类似的方法依次表示-1,-2,-3,…
圆周率π是正数,但不是有理数,千万要注意,类似,-等同样也不是有理数.
数轴的认识
-5 -4 -3 -2 -1 0 1 2 3 4 5 6
-
分数或小数也可以用数轴上的点表示,例如从原点向右6.5个
单位长度的点表示小数6.5,从原点向左个单位长度的点表示分数-
圆周率π是正数,但不是有理数,千万要注意,类似,-等同样也不是有理数.
数轴的认识
0
原点
-1
-2
-3
1
2
3
单位长度
水平直线
正方向
画数轴的注意事项:
(1)原点、单位长度和正方向三要素缺一不可;
(2)直线一般画水平的;
(3)正方向用箭头表示,一般取从左到右;
(4)取单位长度应结合实际需要,但要做到刻度均匀.
是正数和负数的分界点;
是数轴的基准点
数轴的点与有理数的关系
归纳: 一般地,设a是一个正数,
则数轴上表示数a在原点的____边,
与原点的距离是____个单位长度;
表示数-a的点在原点的____边,
与原点的距离是____个单位长度.
任何一个有理数都可以用数轴上的一个点来表示.
0是正负数的分界点.
练习1.
课堂练习
练习1.如图,写出数轴上A,B,C,D,E表示的数
-3 -2 -1 0 1 2 3
E
C
D
A
B
答:A:0
B:-2
C:1
D:2.5
E:-3
圆周率π是正数,但不是有理数,千万要注意,类似,-等同样也不是有理数.
课堂练习
练习2.画出数轴并表示下列有理数;
1.5,-2,2,-2.5, ,0
0
1
2
-1
-2
-3
-2.5
0
2
-2
-1.5
3
4
5
圆周率π是正数,但不是有理数,千万要注意,类似,-等同样也不是有理数.
课堂练习
练习3.数轴上,如果表示数a的点在原点的左边,那么a是一个 ( )数;如果表示数b的点在原点的右边,那么b是一个( )数。
负
正
圆周率π是正数,但不是有理数,千万要注意,类似,-等同样也不是有理数.
数轴的点与有理数的关系
练习4.下列各图是数轴吗?说明你的理由。
不是,没有正方向
(1)
(2)
(3)
(4)
0
-3 -2 -1 1 2 3
-3 -2 -1 1 2 3 4
0
不是,没有原点
不是,没有单位长度
不是,单位长度不一样,且没有原点
圆周率π是正数,但不是有理数,千万要注意,类似,-等同样也不是有理数.
数轴
数轴
认识数轴
数轴上的点与有理数的关系
规定了原点、正方向和单位长度的直线叫数轴.
0是正负数的分界限.
所有的有理数都可以用数轴上的点来表示
原点右边的数是正数,原点左边的数是负数
课后作业
1. 关于数轴,下列说法最准确的是( )
A. 一条直线
B. 有原点、正方向的一条直线
C. 有单位长度的一条直线
D. 规定了原点、正方向、单位长度的直线
2.数轴上的点A到原点的距离是4个单位长度,则点A表示的数是( )
3.在数轴上到表示-2的点相距8个单位长度的点表示的数为________.
D
4或-4
6或-10
人教版数学七年级上册
祝各位同学们学业进步,天天向上!
THE END
人教版数学七年级上册——第一章
《有理数》
1.2.2数轴
05
06
课堂小结
07
教学目标
01
学习任务
02
数轴的认识
03
新课导入
04
课后作业
有理数与数轴上的点的关系
1.能判断一个数是正数还是负数,能用正数或负数表示生活中具有相反意义的量.
2.借助生活中的实例理解有理数的意义,体会负数引入的必要性和有理 数应用的广泛性.
3.培养学生主动探索,积极思考的学习兴趣培养学生积极思考,合作交流的意识和能 力.
教学目的
了解数值的概念,会使用数轴上的点表示有理数.
掌握数轴三要素和有理数集中,原点和数的符号之间的对应关系。
学习任务
1.认识数轴
2.数轴上的点与有理数的关系
新课导入
在一条东西向的马路上,有一个汽车站牌,汽车站牌东3m和7.5m处有一棵柳树和一棵杨树,汽车站西3m和4.8m处分别有一棵槐树和一根电线杆,试画图表示这一情境.
杨树
槐树
柳树
电线杆
汽车站牌
0
东3m
东7.5m
3
7.5
西3m
3
西4.8m
4.8
新课导入
怎样简明地表示这些树、电线杆与汽车站牌的相对位置关系(方向、距离)?
杨树
槐树
柳树
电线杆
汽车站牌
0
东3m
东7.5m
3
7.5
西3m
3
西4.8m
4.8
数轴的认识
为了使表达更清楚,我们规定向东为正,把汽车站牌左右两边的位置对应的距离分别用负数和正数表示.
0
3
7.5
-3
-4.8
把正数、0和负数用一条直线上的点表示出来.
圆周率π是正数,但不是有理数,千万要注意,类似,-等同样也不是有理数.
数轴的认识
思考:右图中的温度计可以看作表示正数、0、负数的直线.
它和下图有什么共同点,有什么不同点?
共同点:都有分界“0”,都有正数、有负数;都有一条直线。
不同点:上图中每两个点之间的长度不一样,而温度计每两个数之间的长度是一样的。
圆周率π是正数,但不是有理数,千万要注意,类似,-等同样也不是有理数.
数轴的认识
在数学上可以用一条直线上的点表示数,这条直线叫做数轴。那什么是数轴呢?
定义:规定了原点、正方向、单位长度的直线叫做数轴。
圆周率π是正数,但不是有理数,千万要注意,类似,-等同样也不是有理数.
数轴的认识
注意:
(1)在直线上任取一点表示数0,这个点叫做原点;
(2)通常规定直线上从原点向右(或上)为正方向,从原点向左(或下)为负方向
(3)选取适当的长度为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表示你1,2,3…;从原点向左,用类似的方法依次表示-1,-2,-3,…
圆周率π是正数,但不是有理数,千万要注意,类似,-等同样也不是有理数.
数轴的认识
-5 -4 -3 -2 -1 0 1 2 3 4 5 6
-
分数或小数也可以用数轴上的点表示,例如从原点向右6.5个
单位长度的点表示小数6.5,从原点向左个单位长度的点表示分数-
圆周率π是正数,但不是有理数,千万要注意,类似,-等同样也不是有理数.
数轴的认识
0
原点
-1
-2
-3
1
2
3
单位长度
水平直线
正方向
画数轴的注意事项:
(1)原点、单位长度和正方向三要素缺一不可;
(2)直线一般画水平的;
(3)正方向用箭头表示,一般取从左到右;
(4)取单位长度应结合实际需要,但要做到刻度均匀.
是正数和负数的分界点;
是数轴的基准点
数轴的点与有理数的关系
归纳: 一般地,设a是一个正数,
则数轴上表示数a在原点的____边,
与原点的距离是____个单位长度;
表示数-a的点在原点的____边,
与原点的距离是____个单位长度.
任何一个有理数都可以用数轴上的一个点来表示.
0是正负数的分界点.
练习1.
课堂练习
练习1.如图,写出数轴上A,B,C,D,E表示的数
-3 -2 -1 0 1 2 3
E
C
D
A
B
答:A:0
B:-2
C:1
D:2.5
E:-3
圆周率π是正数,但不是有理数,千万要注意,类似,-等同样也不是有理数.
课堂练习
练习2.画出数轴并表示下列有理数;
1.5,-2,2,-2.5, ,0
0
1
2
-1
-2
-3
-2.5
0
2
-2
-1.5
3
4
5
圆周率π是正数,但不是有理数,千万要注意,类似,-等同样也不是有理数.
课堂练习
练习3.数轴上,如果表示数a的点在原点的左边,那么a是一个 ( )数;如果表示数b的点在原点的右边,那么b是一个( )数。
负
正
圆周率π是正数,但不是有理数,千万要注意,类似,-等同样也不是有理数.
数轴的点与有理数的关系
练习4.下列各图是数轴吗?说明你的理由。
不是,没有正方向
(1)
(2)
(3)
(4)
0
-3 -2 -1 1 2 3
-3 -2 -1 1 2 3 4
0
不是,没有原点
不是,没有单位长度
不是,单位长度不一样,且没有原点
圆周率π是正数,但不是有理数,千万要注意,类似,-等同样也不是有理数.
数轴
数轴
认识数轴
数轴上的点与有理数的关系
规定了原点、正方向和单位长度的直线叫数轴.
0是正负数的分界限.
所有的有理数都可以用数轴上的点来表示
原点右边的数是正数,原点左边的数是负数
课后作业
1. 关于数轴,下列说法最准确的是( )
A. 一条直线
B. 有原点、正方向的一条直线
C. 有单位长度的一条直线
D. 规定了原点、正方向、单位长度的直线
2.数轴上的点A到原点的距离是4个单位长度,则点A表示的数是( )
3.在数轴上到表示-2的点相距8个单位长度的点表示的数为________.
D
4或-4
6或-10
人教版数学七年级上册
祝各位同学们学业进步,天天向上!
THE END
