人教版数学八年级上册 11.2 与三角形有关的角 同步练习卷(含答案)
文档属性
| 名称 | 人教版数学八年级上册 11.2 与三角形有关的角 同步练习卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 144.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-17 20:10:15 | ||
图片预览



文档简介
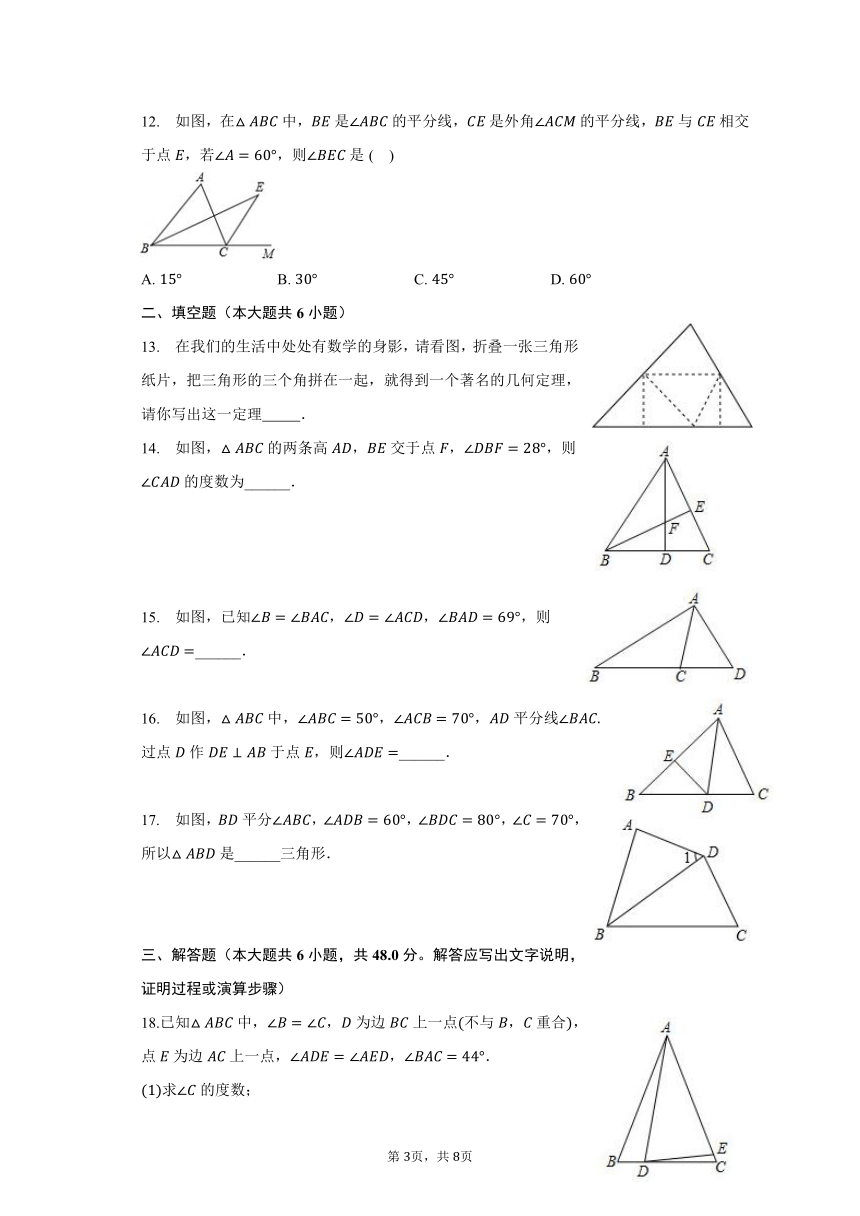
八年级上册《11.2 与三角形有关的角》同步练习卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共12小题,在每小题列出的选项中,选出符合题目的一项)
1. 一个三角形三个内角的度数之比为::,这个三角形一定是( )
A. 直角三角形 B. 等腰三角形 C. 锐角三角形 D. 钝角三角形
2. 如图,三角形,,是三角形的高,图中相等的是( )
A. B.
C. D.
3. 如图,是的角平分线,若,,则的度数是( )
A.
B.
C.
D.
4. 如图,在中,和是角平分线,其交点为,若,则的度数( )
A. B. C. D.
5. 如图,点在的延长线上,于点,交于点若,,则的度数为( )
A. B. C. D.
6. 在中,若一个内角等于另外两个内角的差,则( )
A. 必有一个内角等于 B. 必有一个内角等于
C. 必有一个内角等于 D. 必有一个内角等于
7. 在中,,则的补角等于( )
A. B. C. D.
8. 如图,在中,点是和的角平分线的交点,,,则为( )
A. B. C. D.
9. 如图,将一副三角板如图放置,若,则( )
A.
B.
C.
D.
10. 在下列条件中,不能确定是直角三角形的条件是( )
A. B.
C. D.
11. 将一副直角三角板按如图所示的位置放置,使含角的三角板的一条直角边和含角的三角板的一条直角边放在同一条直线上,则的度数是( )
A.
B.
C.
D.
12. 如图,在中,是的平分线,是外角的平分线,与相交于点,若,则是( )
A. B. C. D.
二、填空题(本大题共6小题)
13. 在我们的生活中处处有数学的身影,请看图,折叠一张三角形纸片,把三角形的三个角拼在一起,就得到一个著名的几何定理,请你写出这一定理 .
14. 如图,的两条高,交于点,,则的度数为______.
15. 如图,已知,,,则______.
16. 如图,中,,,平分线过点作于点,则______.
17. 如图,平分,,,,所以是______三角形.
三、解答题(本大题共6小题,共48.0分。解答应写出文字说明,证明过程或演算步骤)
18.已知中,,为边上一点不与,重合,点为边上一点,,.
求的度数;
若,求的度数.
19. 一个零件的形状如图所示,按规定,和分别是和的零件为合格零件,现质检工人量得,就断定这个零件不合格,请你运用三角形的有关知识说明零件不合格的理由.
20. 如图,在中,,,的外角的平分线交的延长线于点.
求的度数;
过点作,交的延长线于点,求的度数.
21. 如图,在中,是边上的高,,分别是和的角平分线,它们相交于点,,求的度数.
22. Ⅰ如图,是锐角三角形,高、相交于点,求出与的数量关系;
Ⅱ如图,是钝角三角形,,高、所在的直线相交于点,把图补充完整,并说明与的数量关系与中的结论是否一致.
23. 问题情景如图,中,有一块直角三角板放置在上点在内,使三角板的两条直角边、恰好分别经过点和点.
试问与是否存在某种确定的数量关系?
特殊探究:若,
则______度,
______度,
______度;
类比探索:请探究与的关系.
类比延伸:如图,改变直角三角板的位置;使点在外,三角板的两条直角边、仍然分别经过点和点,中的结论是否仍然成立?若不成立,请直接写出你的结论.
答案
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
13. 三角形的内角和是 14. 15. 16. 17. 直角
18. 解:,
,
,
,
;
,,
,
,
,
,
.
19. 解:如图,延长交于,
,,
,
,
.
又,
这个零件不合格.
20. 解:在中,,,
.
是的平分线,
;
,,
.
,
.
21. 解:,
,
,分别是和的角平分线,它们相交于点,
,
,
是边上的高,
,
,
即的度数是.
22. 解:Ⅰ结论:.
理由:高、相交于点,
,
在四边形中,,
,
,
Ⅱ图形如图所示,结论不变..
理由:在四边形中,,
,
,
.
23. ;;
结论:.
证明:,
,
.
不成立; 存在 .
理由:中,,
,
,
,
即,
.
第1页,共1页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共12小题,在每小题列出的选项中,选出符合题目的一项)
1. 一个三角形三个内角的度数之比为::,这个三角形一定是( )
A. 直角三角形 B. 等腰三角形 C. 锐角三角形 D. 钝角三角形
2. 如图,三角形,,是三角形的高,图中相等的是( )
A. B.
C. D.
3. 如图,是的角平分线,若,,则的度数是( )
A.
B.
C.
D.
4. 如图,在中,和是角平分线,其交点为,若,则的度数( )
A. B. C. D.
5. 如图,点在的延长线上,于点,交于点若,,则的度数为( )
A. B. C. D.
6. 在中,若一个内角等于另外两个内角的差,则( )
A. 必有一个内角等于 B. 必有一个内角等于
C. 必有一个内角等于 D. 必有一个内角等于
7. 在中,,则的补角等于( )
A. B. C. D.
8. 如图,在中,点是和的角平分线的交点,,,则为( )
A. B. C. D.
9. 如图,将一副三角板如图放置,若,则( )
A.
B.
C.
D.
10. 在下列条件中,不能确定是直角三角形的条件是( )
A. B.
C. D.
11. 将一副直角三角板按如图所示的位置放置,使含角的三角板的一条直角边和含角的三角板的一条直角边放在同一条直线上,则的度数是( )
A.
B.
C.
D.
12. 如图,在中,是的平分线,是外角的平分线,与相交于点,若,则是( )
A. B. C. D.
二、填空题(本大题共6小题)
13. 在我们的生活中处处有数学的身影,请看图,折叠一张三角形纸片,把三角形的三个角拼在一起,就得到一个著名的几何定理,请你写出这一定理 .
14. 如图,的两条高,交于点,,则的度数为______.
15. 如图,已知,,,则______.
16. 如图,中,,,平分线过点作于点,则______.
17. 如图,平分,,,,所以是______三角形.
三、解答题(本大题共6小题,共48.0分。解答应写出文字说明,证明过程或演算步骤)
18.已知中,,为边上一点不与,重合,点为边上一点,,.
求的度数;
若,求的度数.
19. 一个零件的形状如图所示,按规定,和分别是和的零件为合格零件,现质检工人量得,就断定这个零件不合格,请你运用三角形的有关知识说明零件不合格的理由.
20. 如图,在中,,,的外角的平分线交的延长线于点.
求的度数;
过点作,交的延长线于点,求的度数.
21. 如图,在中,是边上的高,,分别是和的角平分线,它们相交于点,,求的度数.
22. Ⅰ如图,是锐角三角形,高、相交于点,求出与的数量关系;
Ⅱ如图,是钝角三角形,,高、所在的直线相交于点,把图补充完整,并说明与的数量关系与中的结论是否一致.
23. 问题情景如图,中,有一块直角三角板放置在上点在内,使三角板的两条直角边、恰好分别经过点和点.
试问与是否存在某种确定的数量关系?
特殊探究:若,
则______度,
______度,
______度;
类比探索:请探究与的关系.
类比延伸:如图,改变直角三角板的位置;使点在外,三角板的两条直角边、仍然分别经过点和点,中的结论是否仍然成立?若不成立,请直接写出你的结论.
答案
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
13. 三角形的内角和是 14. 15. 16. 17. 直角
18. 解:,
,
,
,
;
,,
,
,
,
,
.
19. 解:如图,延长交于,
,,
,
,
.
又,
这个零件不合格.
20. 解:在中,,,
.
是的平分线,
;
,,
.
,
.
21. 解:,
,
,分别是和的角平分线,它们相交于点,
,
,
是边上的高,
,
,
即的度数是.
22. 解:Ⅰ结论:.
理由:高、相交于点,
,
在四边形中,,
,
,
Ⅱ图形如图所示,结论不变..
理由:在四边形中,,
,
,
.
23. ;;
结论:.
证明:,
,
.
不成立; 存在 .
理由:中,,
,
,
,
即,
.
第1页,共1页
