九年级数学(上)第24章《圆》周练(一)(含答案)
文档属性
| 名称 | 九年级数学(上)第24章《圆》周练(一)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 270.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-18 19:15:48 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
15.九年级数学(上)第24章《圆》周练(一)
(考试范围:第24.1—圆解答参考时间:90分钟满分:120分)
一、选择题(每小题3分,共30分)
1.如图,AB是的弦,∠AOB=90°,若OA=3,则AB的长为( )
A.4 B. D.3
2.如图,在中,的半径为5cm,弦AB的长为8cm,M是AB上任意一点,则OM的最小值为( )
A.4cm B.5cm C.6cm D.3cm
3.如图,点A,B,C都在上,若∠AOB+∠ACB=99°,则∠ACB的大小是( )
A.20° B.25° C.30° D.33°
4.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD=115,则∠DCE的大小是( )
A.115° B.105° C.100° D.95°
5.如图,A,B,C是上的三点,D为BC的中点,∠BOD=40°,则∠CAD的度数为( )
A.40° B.30° C.25° D.20°
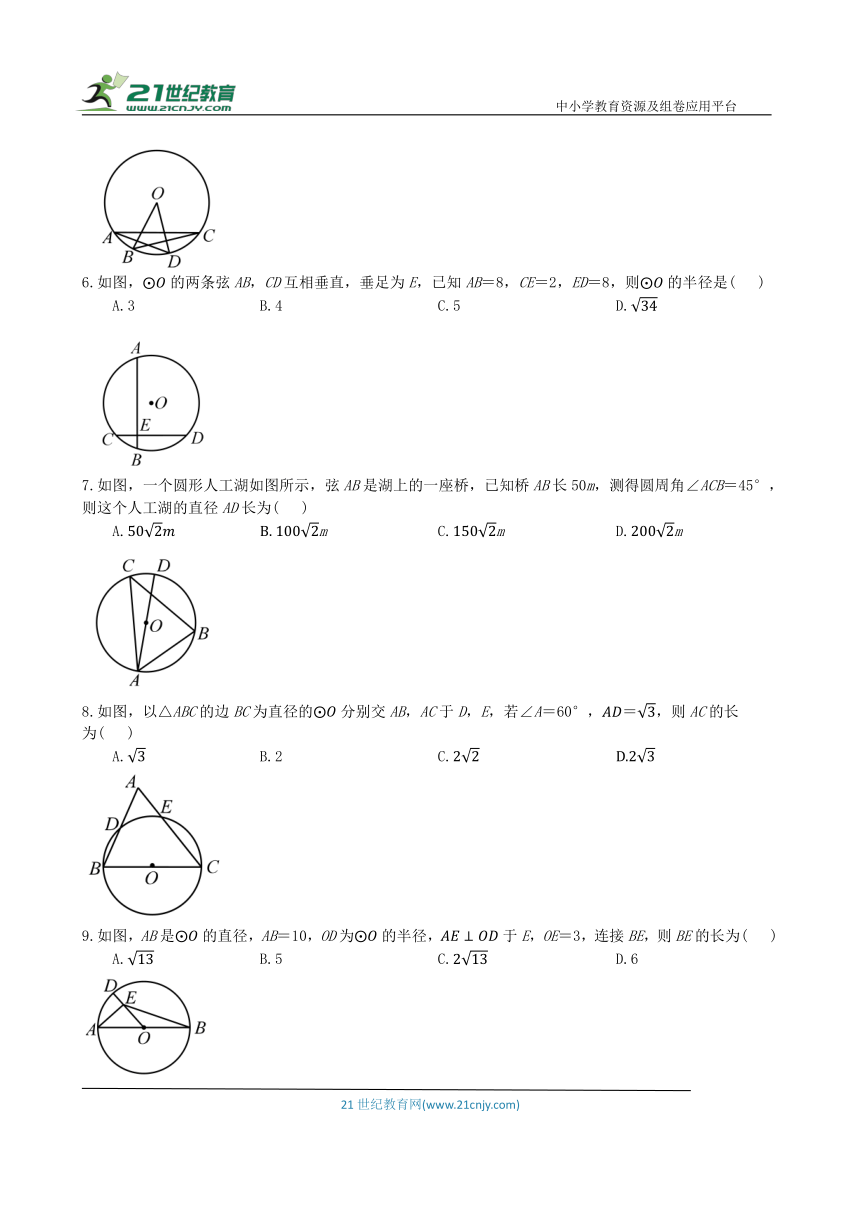
6.如图,的两条弦AB,CD互相垂直,垂足为E,已知AB=8,CE=2,ED=8,则的半径是( )
A.3 B.4 C.5 D.
7.如图,一个圆形人工湖如图所示,弦AB是湖上的一座桥,已知桥AB长50m,测得圆周角∠ACB=45°,则这个人工湖的直径AD长为( )
A. m C.m D.m
8.如图,以△ABC的边BC为直径的分别交AB,AC于D,E,若∠A=60°,,则AC的长
为( )
A. B.2 C.
9.如图,AB是的直径,AB=10,OD为的半径,于E,OE=3,连接BE,则BE的长为( )
A. B.5 C. D.6
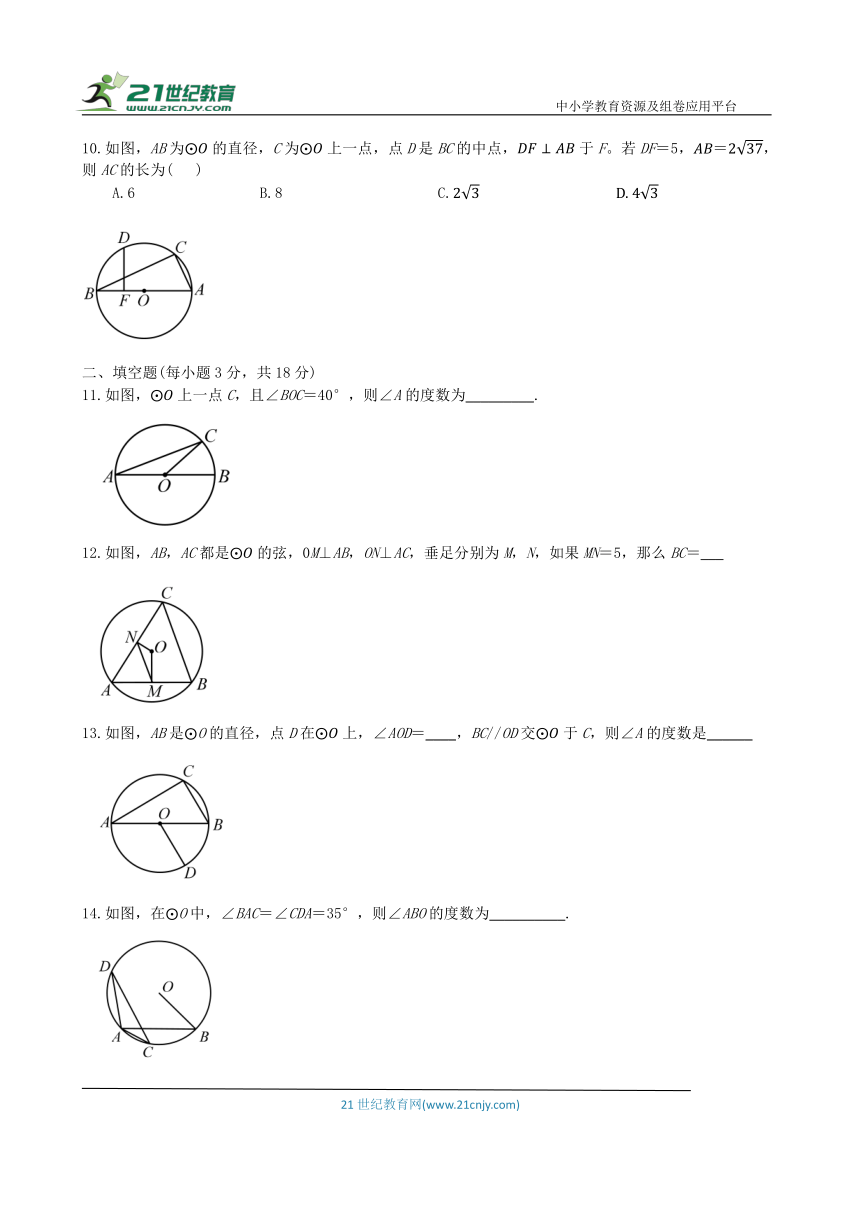
10.如图,AB为的直径,C为上一点,点D是BC的中点,于F。若DF=5,,则AC的长为( )
A.6 B.8 C.
二、填空题(每小题3分,共18分)
11.如图,上一点C,且∠BOC=40°,则∠A的度数为_________.
12.如图,AB,AC都是的弦,0M⊥AB,ON⊥AC,垂足分别为M,N,如果MN=5,那么BC=___
13.如图,AB是 O的直径,点D在上,∠AOD=____,BC//OD交于C,则∠A的度数是______
14.如图,在 O中,∠BAC=∠CDA=35°,则∠ABO的度数为__________.
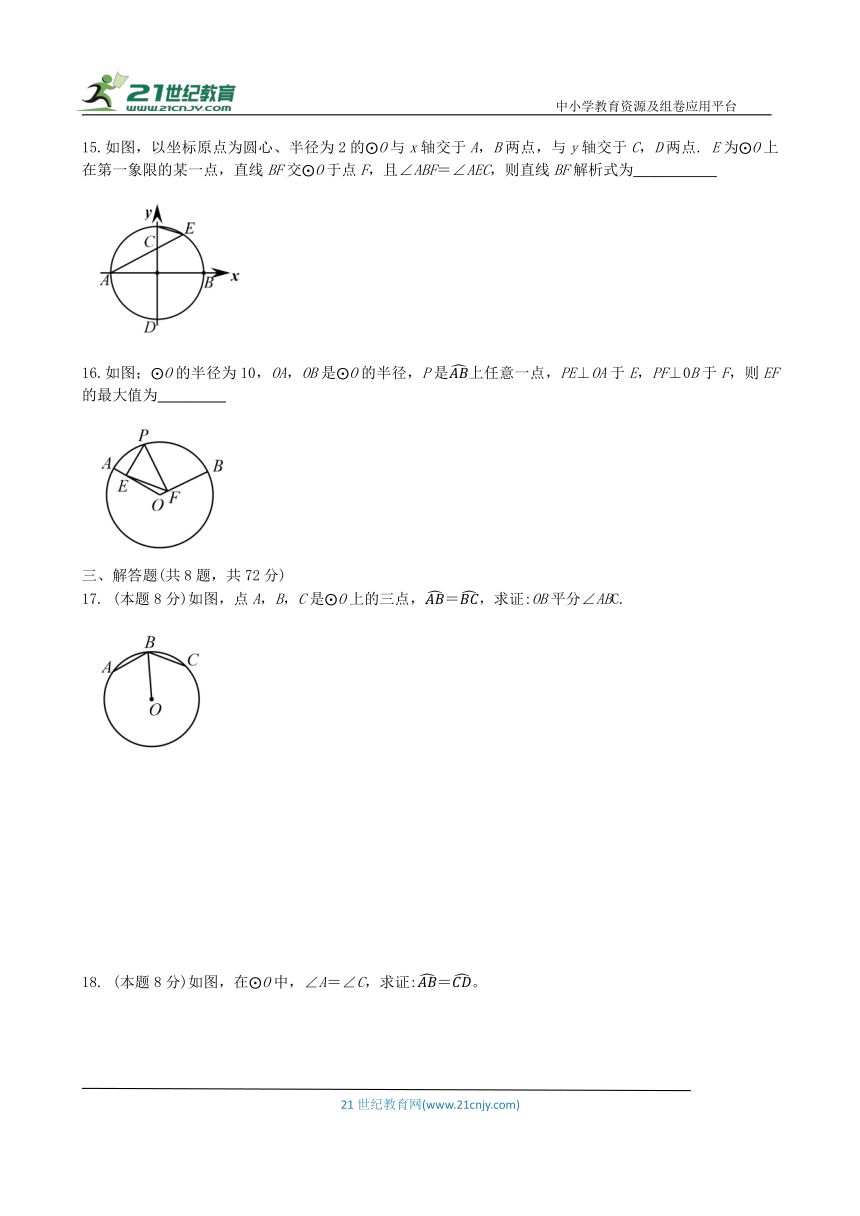
15.如图,以坐标原点为圆心、半径为2的 O与x轴交于A,B两点,与y轴交于C,D两点. E为 O上在第一象限的某一点,直线BF交 O于点F,且∠ABF=∠AEC,则直线BF解析式为___________
16.如图; O的半径为10,OA,OB是 O的半径,P是上任意一点,PE⊥OA于E,PF⊥0B于F,则EF的最大值为_________
三、解答题(共8题,共72分)
17. (本题8分)如图,点A,B,C是 O上的三点,,求证:OB平分∠ABC.
18. (本题8分)如图,在 O中,∠A=∠C,求证:。
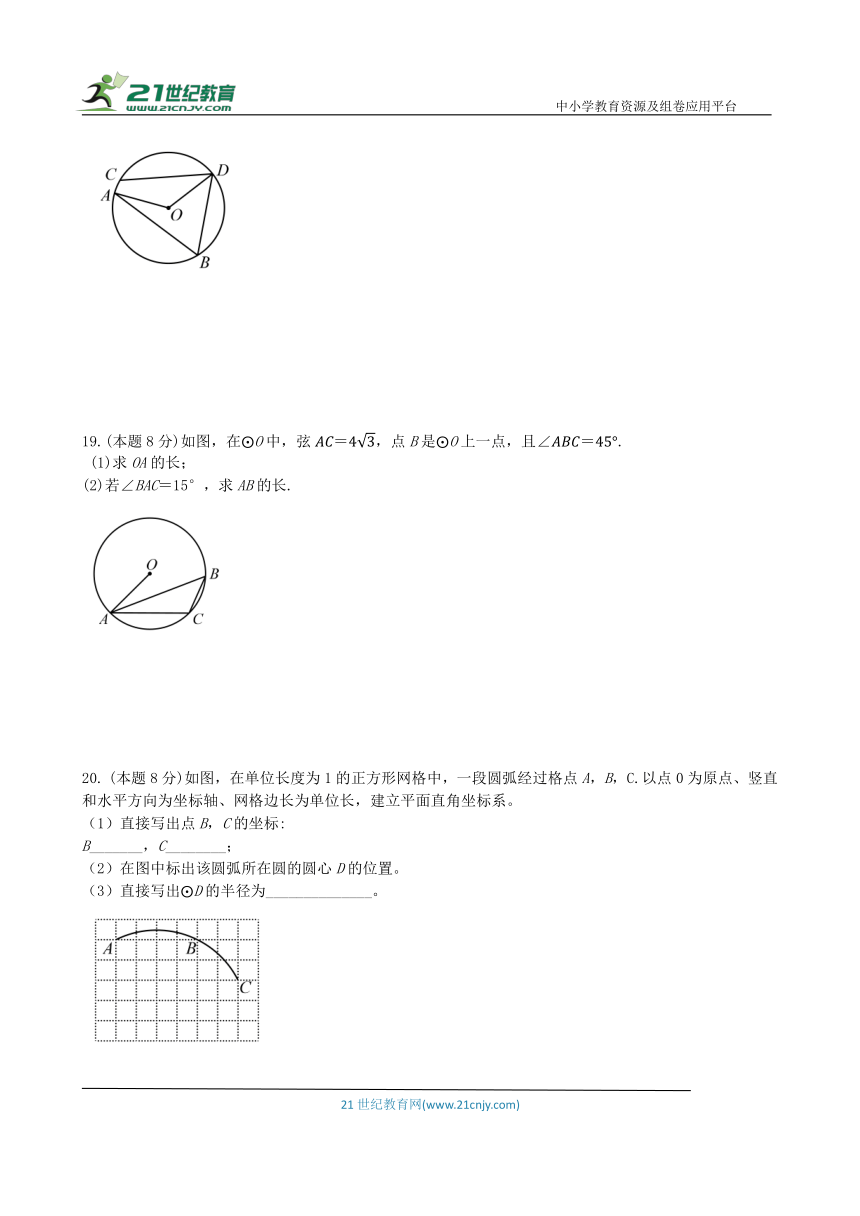
19.(本题8分)如图,在 O中,弦,点B是 O上一点,且.
(1)求OA的长;
(2)若∠BAC=15°,求AB的长.
20. (本题8分)如图,在单位长度为1的正方形网格中,一段圆弧经过格点A,B,C.以点0为原点、竖直和水平方向为坐标轴、网格边长为单位长,建立平面直角坐标系。
(1)直接写出点B,C的坐标:
B_______,C________;
(2)在图中标出该圆弧所在圆的圆心D的位置。
(3)直接写出 D的半径为______________。
21. (本题8分)如图,AD,BC为 O的两条弦,AD⊥BC于E。
(1)求证:∠BCD=∠OAC;
(2)若∠ACB=30°,,求CD的长。
22. (本题10分)如图,△ABC中,∠ABC=90°,以AB为直径的 O交AC于点D,E为上一点,且∠EAB=∠C。
(1)延长BE交AC于点F,求证:AF=CF;
(2)若,,求AE的长。
23.(本题10分)如图,AB,CD是00的两条互相垂直的直径,E是上一点,OG//AE交CE于点G.
(1)求证: ;
(2)求的值。
24. (本题12分)(课本P87例4再探)已知AB为 O的直径,,C为 O上一点,连接AC,AD,CD。
【探索结论】(1)如图1,用旋转的思想证明:,
(2)如图2,直接写出CA,CB,CD之间的关系式;
【结论应用】
(3)如图3,∠ACB=90°,AC=BC,点P为AB的中点,点E满足,点Q为AE的中点,求的值;
15.九年级数学(上)第24章《圆》周练(一)
(考试范围:第24.1—圆解答参考时间:90分钟满分:120分)
一、选择题(每小题3分,共30分)
1.如图,AB是的弦,∠AOB=90°,若OA=3,则AB的长为( D )
A.4 B. D.3
2.如图,在中,的半径为5cm,弦AB的长为8cm,M是AB上任意一点,则OM的最小值为( D)
A.4cm B.5cm C.6cm D.3cm
3.如图,点A,B,C都在上,若∠AOB+∠ACB=99°,则∠ACB的大小是( D )
A.20° B.25° C.30° D.33°
4.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD=115,则∠DCE的大小是( A )
A.115° B.105° C.100° D.95°
5.如图,A,B,C是上的三点,D为BC的中点,∠BOD=40°,则∠CAD的度数为( D )
A.40° B.30° C.25° D.20°
6.如图,的两条弦AB,CD互相垂直,垂足为E,已知AB=8,CE=2,ED=8,则的半径是( C )
A.3 B.4 C.5 D.
7.如图,一个圆形人工湖如图所示,弦AB是湖上的一座桥,已知桥AB长50m,测得圆周角∠ACB=45°,则这个人工湖的直径AD长为( A )
A. m C.m D.m
8.如图,以△ABC的边BC为直径的分别交AB,AC于D,E,若∠A=60°,,则AC的长
为( D )
A. B.2 C.
9.如图,AB是的直径,AB=10,OD为的半径,于E,OE=3,连接BE,则BE的长为( C )
A. B.5 C. D.6
10.如图,AB为的直径,C为上一点,点D是BC的中点,于F。若DF=5,,则AC的长为( D )
A.6 B.8 C.
解:作OE⊥AC于E,易证△OEA≌△DFO,,
二、填空题(每小题3分,共18分)
11.如图,上一点C,且∠BOC=40°,则∠A的度数为20°.
12.如图,AB,AC都是的弦,0M⊥AB,ON⊥AC,垂足分别为M,N,如果MN=5,那么BC=10
13.如图,AB是 O的直径,点D在上,∠AOD=125°,BC//OD交于C,则∠A的度数是35°
14.如图,在 O中,∠BAC=∠CDA=35°,则∠ABO的度数为20° .
15.如图,以坐标原点为圆心、半径为2的 O与x轴交于A,B两点,与y轴交于C,D两点. E为 O上在第一象限的某一点,直线BF交 O于点F,且∠ABF=∠AEC,则直线BF解析式为y=-x+2或y=x-2
16.如图; O的半径为10,OA,OB是 O的半径,P是上任意一点,PE⊥OA于E,PF⊥0B于F,则EF的最大值为10.
解:延长PE交 O于C,延长PF交 O于D,则,当CD为直径时,EF最大。
三、解答题(共8题,共72分)
17.(本题8分)如图,点A,B,C是 O上的三点,,求证:OB平分∠ABC.
证:连OA,OC,证△ABO≌△CBO.
18.(本题8分)如图,在 O中,∠A=∠C,求证:。
证:连OB,OD,证∠AOB=∠COD即可.
19. (本题8分)如图,在 O中,弦,点B是 O上一点,且.
(1)求OA的长;
(2)若∠BAC=15°,求AB的长.
解:(1)连接OC,则;
(2)延长AO交 O于E,则。
20.(本题8分)如图,在单位长度为1的正方形网格中,一段圆弧经过格点A,B,C.以点0为原点、竖直和水平方向为坐标轴、网格边长为单位长,建立平面直角坐标系。
(1)直接写出点B,C的坐标:
B_______,C________;
(2)在图中标出该圆弧所在圆的圆心D的位置。
(3)直接写出 D的半径为______________。
解:(1)B(4,4),C(6,2) (2)D(2,0) (3)
21.(本题8分)如图,AD,BC为 O的两条弦,AD⊥BC于E。
(1)求证:∠BCD=∠OAC;
(2)若∠ACB=30°,,求CD的长。
解:(1)作直径AF,连接CF,AB,则∠ABC=∠AFC,
(2)连接BF,DF,
22. (本题10分)如图,△ABC中,∠ABC=90°,以AB为直径的 O交AC于点D,E为上一点,且∠EAB=∠C。
(1)延长BE交AC于点F,求证:AF=CF;
(2)若,,求AE的长。
解:(1)易证
(2)连接DE,BD。易证
23. (本题10分)如图,AB,CD是00的两条互相垂直的直径,E是上一点,OG//AE交CE于点G.
(1)求证: ;
(2)求的值。
解:(1)延长GO交BE于点H,易证
(2)作交CE于H,连接AH,
24. (本题12分)(课本P87例4再探)已知AB为 O的直径,,C为 O上一点,连接AC,AD,CD。
【探索结论】(1)如图1,用旋转的思想证明:,
(2)如图2,直接写出CA,CB,CD之间的关系式;
解:(1)连DA,DB,将△DBC绕点D逆时针旋转90°得△DAE,证C,A,E共线,
【结论应用】
(3)如图3,∠ACB=90°,AC=BC,点P为AB的中点,点E满足,点Q为AE的中点,求的值;
解:(3)连CQ,CP,则CP⊥AB,CQ⊥AE,易证A,Q,C,P共圆,由(1)知,设。
21世纪教育网(www.21cnjy.com)
15.九年级数学(上)第24章《圆》周练(一)
(考试范围:第24.1—圆解答参考时间:90分钟满分:120分)
一、选择题(每小题3分,共30分)
1.如图,AB是的弦,∠AOB=90°,若OA=3,则AB的长为( )
A.4 B. D.3
2.如图,在中,的半径为5cm,弦AB的长为8cm,M是AB上任意一点,则OM的最小值为( )
A.4cm B.5cm C.6cm D.3cm
3.如图,点A,B,C都在上,若∠AOB+∠ACB=99°,则∠ACB的大小是( )
A.20° B.25° C.30° D.33°
4.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD=115,则∠DCE的大小是( )
A.115° B.105° C.100° D.95°
5.如图,A,B,C是上的三点,D为BC的中点,∠BOD=40°,则∠CAD的度数为( )
A.40° B.30° C.25° D.20°
6.如图,的两条弦AB,CD互相垂直,垂足为E,已知AB=8,CE=2,ED=8,则的半径是( )
A.3 B.4 C.5 D.
7.如图,一个圆形人工湖如图所示,弦AB是湖上的一座桥,已知桥AB长50m,测得圆周角∠ACB=45°,则这个人工湖的直径AD长为( )
A. m C.m D.m
8.如图,以△ABC的边BC为直径的分别交AB,AC于D,E,若∠A=60°,,则AC的长
为( )
A. B.2 C.
9.如图,AB是的直径,AB=10,OD为的半径,于E,OE=3,连接BE,则BE的长为( )
A. B.5 C. D.6
10.如图,AB为的直径,C为上一点,点D是BC的中点,于F。若DF=5,,则AC的长为( )
A.6 B.8 C.
二、填空题(每小题3分,共18分)
11.如图,上一点C,且∠BOC=40°,则∠A的度数为_________.
12.如图,AB,AC都是的弦,0M⊥AB,ON⊥AC,垂足分别为M,N,如果MN=5,那么BC=___
13.如图,AB是 O的直径,点D在上,∠AOD=____,BC//OD交于C,则∠A的度数是______
14.如图,在 O中,∠BAC=∠CDA=35°,则∠ABO的度数为__________.
15.如图,以坐标原点为圆心、半径为2的 O与x轴交于A,B两点,与y轴交于C,D两点. E为 O上在第一象限的某一点,直线BF交 O于点F,且∠ABF=∠AEC,则直线BF解析式为___________
16.如图; O的半径为10,OA,OB是 O的半径,P是上任意一点,PE⊥OA于E,PF⊥0B于F,则EF的最大值为_________
三、解答题(共8题,共72分)
17. (本题8分)如图,点A,B,C是 O上的三点,,求证:OB平分∠ABC.
18. (本题8分)如图,在 O中,∠A=∠C,求证:。
19.(本题8分)如图,在 O中,弦,点B是 O上一点,且.
(1)求OA的长;
(2)若∠BAC=15°,求AB的长.
20. (本题8分)如图,在单位长度为1的正方形网格中,一段圆弧经过格点A,B,C.以点0为原点、竖直和水平方向为坐标轴、网格边长为单位长,建立平面直角坐标系。
(1)直接写出点B,C的坐标:
B_______,C________;
(2)在图中标出该圆弧所在圆的圆心D的位置。
(3)直接写出 D的半径为______________。
21. (本题8分)如图,AD,BC为 O的两条弦,AD⊥BC于E。
(1)求证:∠BCD=∠OAC;
(2)若∠ACB=30°,,求CD的长。
22. (本题10分)如图,△ABC中,∠ABC=90°,以AB为直径的 O交AC于点D,E为上一点,且∠EAB=∠C。
(1)延长BE交AC于点F,求证:AF=CF;
(2)若,,求AE的长。
23.(本题10分)如图,AB,CD是00的两条互相垂直的直径,E是上一点,OG//AE交CE于点G.
(1)求证: ;
(2)求的值。
24. (本题12分)(课本P87例4再探)已知AB为 O的直径,,C为 O上一点,连接AC,AD,CD。
【探索结论】(1)如图1,用旋转的思想证明:,
(2)如图2,直接写出CA,CB,CD之间的关系式;
【结论应用】
(3)如图3,∠ACB=90°,AC=BC,点P为AB的中点,点E满足,点Q为AE的中点,求的值;
15.九年级数学(上)第24章《圆》周练(一)
(考试范围:第24.1—圆解答参考时间:90分钟满分:120分)
一、选择题(每小题3分,共30分)
1.如图,AB是的弦,∠AOB=90°,若OA=3,则AB的长为( D )
A.4 B. D.3
2.如图,在中,的半径为5cm,弦AB的长为8cm,M是AB上任意一点,则OM的最小值为( D)
A.4cm B.5cm C.6cm D.3cm
3.如图,点A,B,C都在上,若∠AOB+∠ACB=99°,则∠ACB的大小是( D )
A.20° B.25° C.30° D.33°
4.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD=115,则∠DCE的大小是( A )
A.115° B.105° C.100° D.95°
5.如图,A,B,C是上的三点,D为BC的中点,∠BOD=40°,则∠CAD的度数为( D )
A.40° B.30° C.25° D.20°
6.如图,的两条弦AB,CD互相垂直,垂足为E,已知AB=8,CE=2,ED=8,则的半径是( C )
A.3 B.4 C.5 D.
7.如图,一个圆形人工湖如图所示,弦AB是湖上的一座桥,已知桥AB长50m,测得圆周角∠ACB=45°,则这个人工湖的直径AD长为( A )
A. m C.m D.m
8.如图,以△ABC的边BC为直径的分别交AB,AC于D,E,若∠A=60°,,则AC的长
为( D )
A. B.2 C.
9.如图,AB是的直径,AB=10,OD为的半径,于E,OE=3,连接BE,则BE的长为( C )
A. B.5 C. D.6
10.如图,AB为的直径,C为上一点,点D是BC的中点,于F。若DF=5,,则AC的长为( D )
A.6 B.8 C.
解:作OE⊥AC于E,易证△OEA≌△DFO,,
二、填空题(每小题3分,共18分)
11.如图,上一点C,且∠BOC=40°,则∠A的度数为20°.
12.如图,AB,AC都是的弦,0M⊥AB,ON⊥AC,垂足分别为M,N,如果MN=5,那么BC=10
13.如图,AB是 O的直径,点D在上,∠AOD=125°,BC//OD交于C,则∠A的度数是35°
14.如图,在 O中,∠BAC=∠CDA=35°,则∠ABO的度数为20° .
15.如图,以坐标原点为圆心、半径为2的 O与x轴交于A,B两点,与y轴交于C,D两点. E为 O上在第一象限的某一点,直线BF交 O于点F,且∠ABF=∠AEC,则直线BF解析式为y=-x+2或y=x-2
16.如图; O的半径为10,OA,OB是 O的半径,P是上任意一点,PE⊥OA于E,PF⊥0B于F,则EF的最大值为10.
解:延长PE交 O于C,延长PF交 O于D,则,当CD为直径时,EF最大。
三、解答题(共8题,共72分)
17.(本题8分)如图,点A,B,C是 O上的三点,,求证:OB平分∠ABC.
证:连OA,OC,证△ABO≌△CBO.
18.(本题8分)如图,在 O中,∠A=∠C,求证:。
证:连OB,OD,证∠AOB=∠COD即可.
19. (本题8分)如图,在 O中,弦,点B是 O上一点,且.
(1)求OA的长;
(2)若∠BAC=15°,求AB的长.
解:(1)连接OC,则;
(2)延长AO交 O于E,则。
20.(本题8分)如图,在单位长度为1的正方形网格中,一段圆弧经过格点A,B,C.以点0为原点、竖直和水平方向为坐标轴、网格边长为单位长,建立平面直角坐标系。
(1)直接写出点B,C的坐标:
B_______,C________;
(2)在图中标出该圆弧所在圆的圆心D的位置。
(3)直接写出 D的半径为______________。
解:(1)B(4,4),C(6,2) (2)D(2,0) (3)
21.(本题8分)如图,AD,BC为 O的两条弦,AD⊥BC于E。
(1)求证:∠BCD=∠OAC;
(2)若∠ACB=30°,,求CD的长。
解:(1)作直径AF,连接CF,AB,则∠ABC=∠AFC,
(2)连接BF,DF,
22. (本题10分)如图,△ABC中,∠ABC=90°,以AB为直径的 O交AC于点D,E为上一点,且∠EAB=∠C。
(1)延长BE交AC于点F,求证:AF=CF;
(2)若,,求AE的长。
解:(1)易证
(2)连接DE,BD。易证
23. (本题10分)如图,AB,CD是00的两条互相垂直的直径,E是上一点,OG//AE交CE于点G.
(1)求证: ;
(2)求的值。
解:(1)延长GO交BE于点H,易证
(2)作交CE于H,连接AH,
24. (本题12分)(课本P87例4再探)已知AB为 O的直径,,C为 O上一点,连接AC,AD,CD。
【探索结论】(1)如图1,用旋转的思想证明:,
(2)如图2,直接写出CA,CB,CD之间的关系式;
解:(1)连DA,DB,将△DBC绕点D逆时针旋转90°得△DAE,证C,A,E共线,
【结论应用】
(3)如图3,∠ACB=90°,AC=BC,点P为AB的中点,点E满足,点Q为AE的中点,求的值;
解:(3)连CQ,CP,则CP⊥AB,CQ⊥AE,易证A,Q,C,P共圆,由(1)知,设。
21世纪教育网(www.21cnjy.com)
同课章节目录
