九年级数学(上)第24章《圆》周练(二)(含答案)
文档属性
| 名称 | 九年级数学(上)第24章《圆》周练(二)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 237.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-18 19:21:43 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
16.九年级数学(上)第24章《圆》周练(二)
(考试范围:第24.2—点和圆的位置关系;点和圆的位置关系参考时间:90分钟满分:120分)
一、选择题(每小题3分,共30分)
1.已知⊙O的半径为5cm,点P到圆心O的距离为4cm,则点P与⊙O的位置关系是( )
A.点P在⊙O外 B.点P在⊙O上
C.点P在⊙O内 D.无法判断
2.⊙O的直径为10,圆心O到直线l的距离为5,则直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.无法确定
3.如图,PA是⊙O的切线,切点为A,,∠APO=30°,则⊙O的半径为( )
A.1 B. C.2 D.4
4.如图,AB为⊙O的直径,圆周角∠ABC=20°,当∠BCD=( )时,CD为⊙O的切线.
A.40° B.50° C.60° D.70°
5.如图,PA,PB是⊙O的切线,A,B为切点,若∠BOA=130°,则∠P的度数是( )
A.35° B.50° C.55° D.65°
6.如图,PA,PB切⊙O于A,B两点,AC是⊙O的直径,∠P=50°,则∠ACB的度数为( )
A.50° B.65° C.70° D.80°
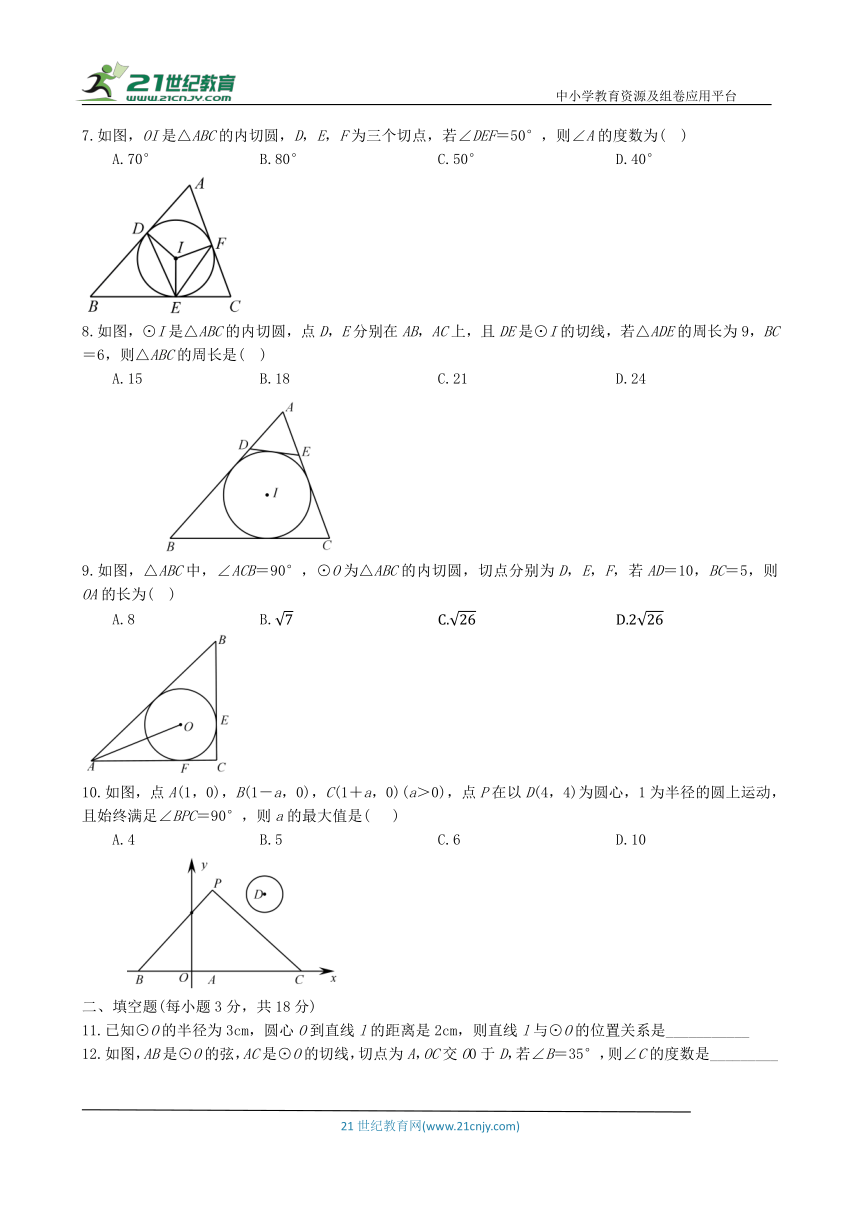
7.如图,OI是△ABC的内切圆,D,E,F为三个切点,若∠DEF=50°,则∠A的度数为( )
A.70° B.80° C.50° D.40°
8.如图,⊙I是△ABC的内切圆,点D,E分别在AB,AC上,且DE是⊙I的切线,若△ADE的周长为9,BC=6,则△ABC的周长是( )
A.15 B.18 C.21 D.24
9.如图,△ABC中,∠ACB=90°,⊙O为△ABC的内切圆,切点分别为D,E,F,若AD=10,BC=5,则OA的长为( )
A.8 B.
10.如图,点A(1,0),B(1-a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是( )
A.4 B.5 C.6 D.10
二、填空题(每小题3分,共18分)
11.已知⊙O的半径为3cm,圆心O到直线l的距离是2cm,则直线l与⊙O的位置关系是___________
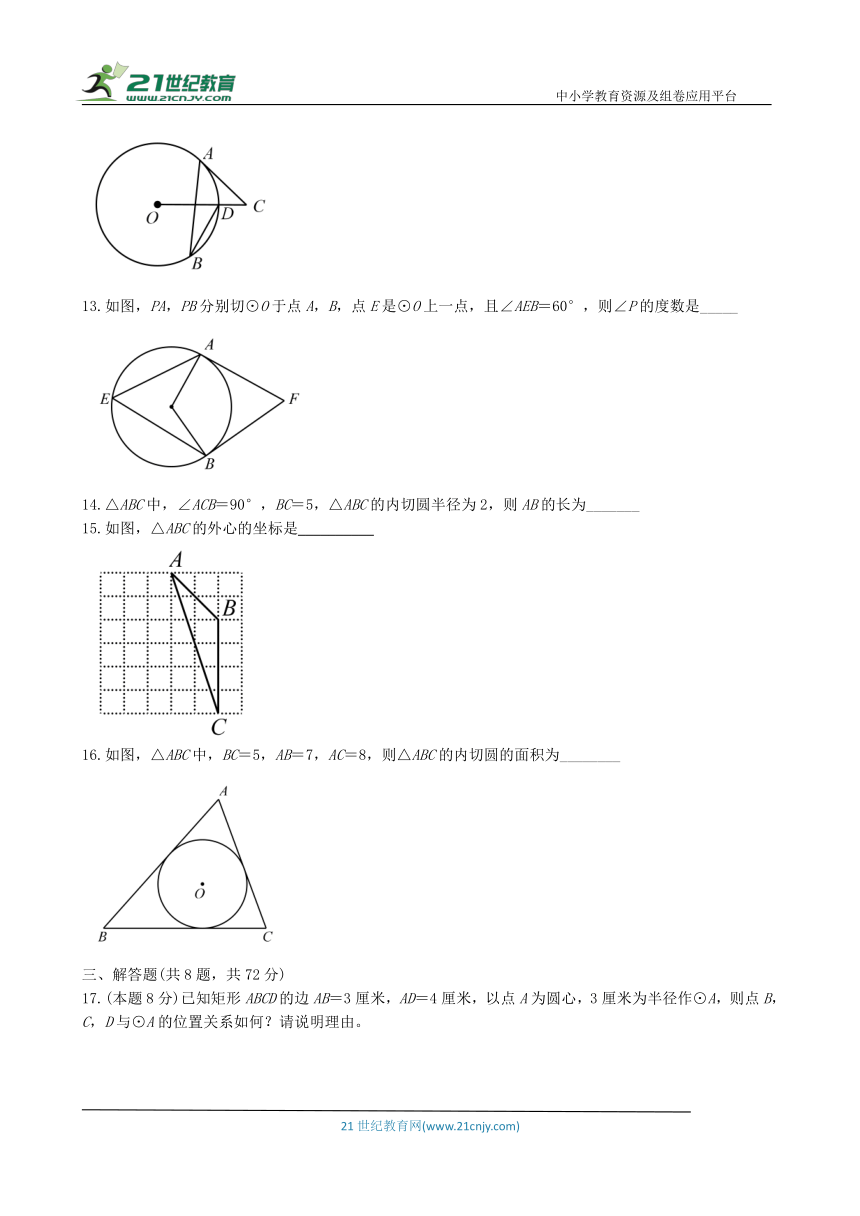
12.如图,AB是⊙O的弦,AC是⊙O的切线,切点为A,OC交O0于D,若∠B=35°,则∠C的度数是_________
13.如图,PA,PB分别切⊙O于点A,B,点E是⊙O上一点,且∠AEB=60°,则∠P的度数是_____
14.△ABC中,∠ACB=90°,BC=5,△ABC的内切圆半径为2,则AB的长为_______
15.如图,△ABC的外心的坐标是__________
16.如图,△ABC中,BC=5,AB=7,AC=8,则△ABC的内切圆的面积为________
三、解答题(共8题,共72分)
17.(本题8分)已知矩形ABCD的边AB=3厘米,AD=4厘米,以点A为圆心,3厘米为半径作⊙A,则点B,C,D与⊙A的位置关系如何?请说明理由。
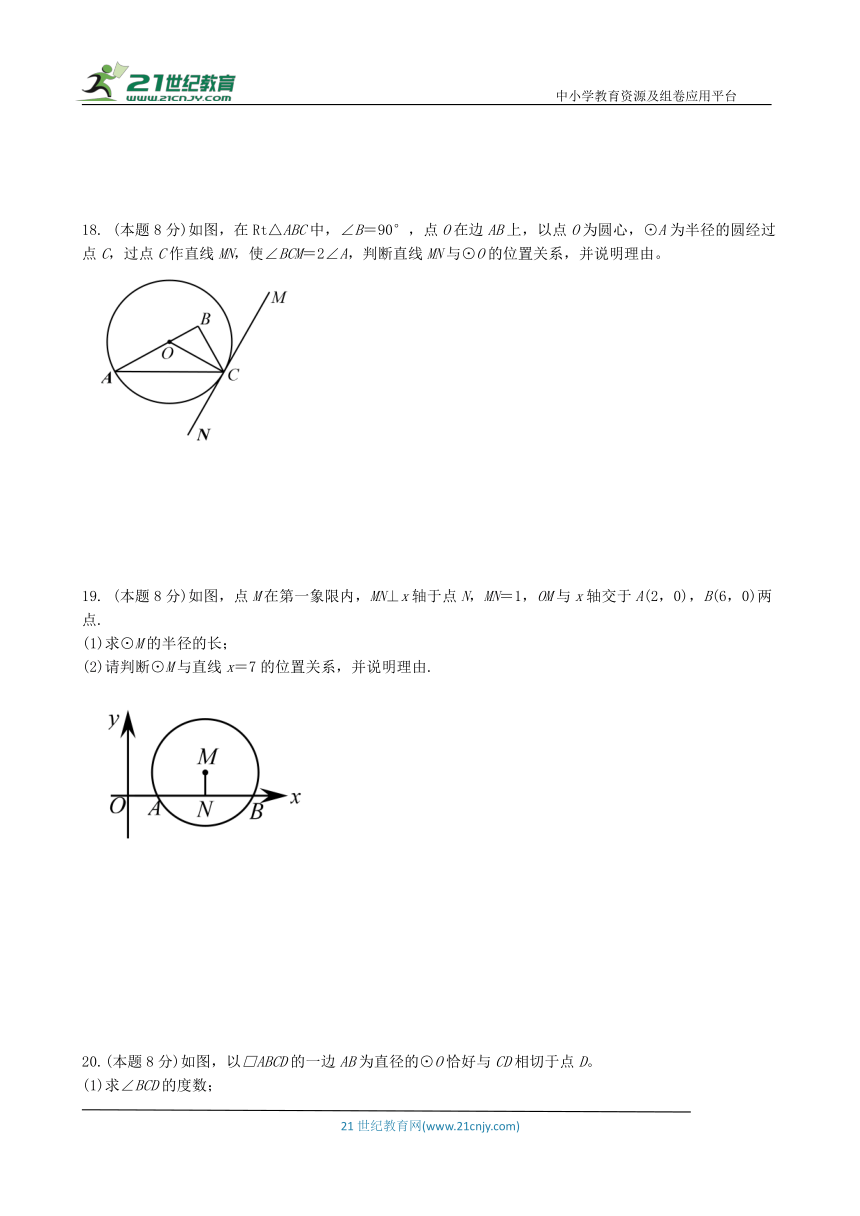
18. (本题8分)如图,在Rt△ABC中,∠B=90°,点O在边AB上,以点O为圆心,⊙A为半径的圆经过点C,过点C作直线MN,使∠BCM=2∠A,判断直线MN与⊙O的位置关系,并说明理由。
19. (本题8分)如图,点M在第一象限内,MN⊥x轴于点N,MN=1,OM与x轴交于A(2,0),B(6,0)两点.
(1)求⊙M的半径的长;
(2)请判断⊙M与直线x=7的位置关系,并说明理由.
20.(本题8分)如图,以□ABCD的一边AB为直径的⊙O恰好与CD相切于点D。
(1)求∠BCD的度数;
(2)连接OC,若AD=4,求OC的长.
21.(本题8分)如图,在△ABC中,AB=AC=10,BC=12,I为△ABC的内心.
(1)求S△ABC;
(2)求BI的长.
22.(本题10分)如图,在Rt△ABC中,∠BAC=90°,O是AB边上的一点,以OA为半径的⊙O与边BC相切于点E。
(1)若AC=5,BC=13,求⊙O的半径长;
(2)过点E作弦EF⊥AB于M,连接AF,若∠F=2∠B,求证:四边形ACEF是菱形.
23.如图,△ABC中,AB=AC,⊙O为△ABC的外接圆,D为⊙O外一点,∠DCA=∠ACB。
(1)求证:CD是⊙O的切线;
(2)连接OD,交AC于点F,若OD⊥AC,当BC=8,⊙O的半径为5时,求CD的长。
24.(本题12分)如图,⊙O为△ABD的外接圆,E为△ABD的内心,DE的延长线交⊙O于点C。
(1)如图1,求证:CE=AC;
(2)如图2,AB为⊙O的直径,AB=10,AD=8。
①求S△ADE;
②求的值。
16.九年级数学(上)第24章《圆》周练(二)
(考试范围:第24.2—点和圆的位置关系;点和圆的位置关系参考时间:90分钟满分:120分)
一、选择题(每小题3分,共30分)
1.已知⊙O的半径为5cm,点P到圆心O的距离为4cm,则点P与⊙O的位置关系是( C )
A.点P在⊙O外 B.点P在⊙O上
C.点P在⊙O内 D.无法判断
2.⊙O的直径为10,圆心O到直线l的距离为5,则直线l与⊙O的位置关系是( B )
A.相交 B.相切 C.相离 D.无法确定
3.如图,PA是⊙O的切线,切点为A,,∠APO=30°,则⊙O的半径为( D)
A.1 B. C.2 D.4
4.如图,AB为⊙O的直径,圆周角∠ABC=20°,当∠BCD=( D )时,CD为⊙O的切线.
A.40° B.50° C.60° D.70°
5.如图,PA,PB是⊙O的切线,A,B为切点,若∠BOA=130°,则∠P的度数是( B )
A.35° B.50° C.55° D.65°
6.如图,PA,PB切⊙O于A,B两点,AC是⊙O的直径,∠P=50°,则∠ACB的度数为( B )
A.50° B.65° C.70° D.80°
7.如图,OI是△ABC的内切圆,D,E,F为三个切点,若∠DEF=50°,则∠A的度数为( B )
A.70° B.80° C.50° D.40°
8.如图,⊙I是△ABC的内切圆,点D,E分别在AB,AC上,且DE是⊙I的切线,若△ADE的周长为9,BC=6,则△ABC的周长是( C )
A.15 B.18 C.21 D.24
9.如图,△ABC中,∠ACB=90°,⊙O为△ABC的内切圆,切点分别为D,E,F,若AD=10,BC=5,则OA的长为( D )
A.8 B.
解:连OE,OF,设⊙O的半径为R,则(10+R)2+52=(15-R)2,R=2。
10.如图,点A(1,0),B(1-a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是( C )
A.4 B.5 C.6 D.10
解:∵A(1,0),B(1-a,0) ,C(1+a,0)(a>0),.AB=1-(1-a)=a,CA=a+1-1=a,
∴AB=AC,∵∠BPC=90°,∴PA=AB=AC=a,延长AD交⊙O于P' ,此时AP'最大,∵A(1,0) ,D(4,4),∴AD=5,∴AP'=5+1=6,.a的最大值为6.
二、填空题(每小题3分,共18分)
11.已知⊙O的半径为3cm,圆心O到直线l的距离是2cm,则直线l与⊙O的位置关系是相交.
12.如图,AB是⊙O的弦,AC是⊙O的切线,切点为A,OC交O0于D,若∠B=35°,则∠C的度数是20°
13.如图,PA,PB分别切⊙O于点A,B,点E是⊙O上一点,且∠AEB=60°,则∠P的度数是60° .
14.△ABC中,∠ACB=90°,BC=5,△ABC的内切圆半径为2,则AB的长为13
15.如图,△ABC的外心的坐标是(-2,-1) .
16.如图,△ABC中,BC=5,AB=7,AC=8,则△ABC的内切圆的面积为3
解:设内切圆的半径为R,过A作AD⊥BC于D,设BD=x,则CD=5-x,由勾股定理得:AB2-BD2=AC2-CD2,即72-x2=8-(5-x)2,解得x=1,AD=,由面积法:BCAD=(AB+BC+AC)R,5×4=20×R,R=,∴S=3。
三、解答题(共8题,共72分)
17. (本题8分)已知矩形ABCD的边AB=3厘米,AD=4厘米,以点A为圆心,3厘米为半径作⊙A,则点B,C,D与⊙A的位置关系如何?请说明理由。
解:点B在⊙A上,点C,D都在⊙A外.
18. (本题8分)如图,在Rt△ABC中,∠B=90°,点O在边AB上,以点O为圆心,⊙A为半径的圆经过点C,过点C作直线MN,使∠BCM=2∠A,判断直线MN与⊙O的位置关系,并说明理由。
解:MN是⊙O切线。理由:连接OC。∵OA=OC,∴∠OAC=∠OCA,∵∠BOC=∠A+∠OCA=2∠A,∠BCM=2∠A,∴∠BCM=∠BOC,∵∠B=90°,∴∠BOC+∠BCO=90°,∴∠BOC+∠BCO=90°,∴OC⊥MN,∴MN是⊙O切线。
19. (本题8分)如图,点M在第一象限内,MN⊥x轴于点N,MN=1,OM与x轴交于A(2,0),B(6,0)两点.
(1)求⊙M的半径的长;
(2)请判断⊙M与直线x=7的位置关系,并说明理由.
解:(1);
(2)易求M(4,1),∴M到x=7的距离d=3>,
∴直线x=7与⊙M相离.
20. (本题8分)如图,以□ABCD的一边AB为直径的⊙O恰好与CD相切于点D。
(1)求∠BCD的度数;
(2)连接OC,若AD=4,求OC的长.
解:(1)连接OD,易证△AOD是等腰直角三角形,
∴∠A=45°=∠BCD;
(2)OA=D=22,CD=AB=4,OC=
21.(本题8分)如图,在△ABC中,AB=AC=10,BC=12,I为△ABC的内心.
(1)求S△ABC;
(2)求BI的长.
解:(1)48;
(2)延长AI交BC于点D,作IE⊥AB于E,则BD=BE=6,AE=4,易求AD=8,设ID=IE=r,则AI=8-r,在△AIE中有:42+r2=(8-r)2,∴r=3,∴BI=。
22.(本题10分)如图,在Rt△ABC中,∠BAC=90°,O是AB边上的一点,以OA为半径的⊙O与边BC相切于点E。
(1)若AC=5,BC=13,求⊙O的半径长;
(2)过点E作弦EF⊥AB于M,连接AF,若∠F=2∠B,求证:四边形ACEF是菱形.
解:(1) CA=CE=5,BE=8,AB=12,设OA=OE=R,OB=12-R,在△OBE中,R2+82= (12一R)2,∴R=;
(2)∵∠AOE=2∠F=4∠B=90°+∠B,∴∠B=30°,∴∠F=60°,∴∠FAB=30°,∴∠FAB=∠B,∴AF//BE,又∵AC// EF,AC=CE,∴四边形ACEF是菱形。
23.如图,△ABC中,AB=AC,⊙O为△ABC的外接圆,D为⊙O外一点,∠DCA=∠ACB。
(1)求证:CD是⊙O的切线;
(2)连接OD,交AC于点F,若OD⊥AC,当BC=8,⊙O的半径为5时,求CD的长。
解:(1)方法一:作直径CM,连接AM,∴∠ACD=∠ACB=∠B=∠M,又∵∠M+∠ACM=90°,∴∠ACD+∠ACM=90°,CD是⊙O的切线;
方法二:连接OC,延长AO交BC于E,∴。∴AE⊥BC,∴∠ACB+∠EAC=90*,∴∠EAC=∠OCA,∴∠ACD+∠OCA=90°,∴CD是⊙O的切线.
(2)延长AO交BC于E,∴AB=AC,∴AE⊥BC,∴BE=CE=4,∴OE=3,∴AE=8,∴AC=,∵OD⊥AC,∵AF=CF=,∴OF=,设DF=x,∴OD2-OC2=CD2=DF2+CF2,∴(x+)2-52=x2+(2)2,x=,∴CD==10。
24.(本题12分)如图,⊙O为△ABD的外接圆,E为△ABD的内心,DE的延长线交⊙O于点C。
(1)如图1,求证:CE=AC;
(2)如图2,AB为⊙O的直径,AB=10,AD=8。
①求S△ADE;
②求的值。
解:(1)连AE,证∠CAE=∠CEA即可。
(2)①作EF⊥AD于F,作EG⊥AB于G,则EF,EG为△ADB内切圆心的半径,∴2DF=AD+BD-AB,∴DF=2=EF,∴S△ADE=ADEF=8。
②∵EF=DF=2,∴AF=AG=6,∴AE==2,由(1)知CE=AC=AB=5,∴=2
21世纪教育网(www.21cnjy.com)
16.九年级数学(上)第24章《圆》周练(二)
(考试范围:第24.2—点和圆的位置关系;点和圆的位置关系参考时间:90分钟满分:120分)
一、选择题(每小题3分,共30分)
1.已知⊙O的半径为5cm,点P到圆心O的距离为4cm,则点P与⊙O的位置关系是( )
A.点P在⊙O外 B.点P在⊙O上
C.点P在⊙O内 D.无法判断
2.⊙O的直径为10,圆心O到直线l的距离为5,则直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.无法确定
3.如图,PA是⊙O的切线,切点为A,,∠APO=30°,则⊙O的半径为( )
A.1 B. C.2 D.4
4.如图,AB为⊙O的直径,圆周角∠ABC=20°,当∠BCD=( )时,CD为⊙O的切线.
A.40° B.50° C.60° D.70°
5.如图,PA,PB是⊙O的切线,A,B为切点,若∠BOA=130°,则∠P的度数是( )
A.35° B.50° C.55° D.65°
6.如图,PA,PB切⊙O于A,B两点,AC是⊙O的直径,∠P=50°,则∠ACB的度数为( )
A.50° B.65° C.70° D.80°
7.如图,OI是△ABC的内切圆,D,E,F为三个切点,若∠DEF=50°,则∠A的度数为( )
A.70° B.80° C.50° D.40°
8.如图,⊙I是△ABC的内切圆,点D,E分别在AB,AC上,且DE是⊙I的切线,若△ADE的周长为9,BC=6,则△ABC的周长是( )
A.15 B.18 C.21 D.24
9.如图,△ABC中,∠ACB=90°,⊙O为△ABC的内切圆,切点分别为D,E,F,若AD=10,BC=5,则OA的长为( )
A.8 B.
10.如图,点A(1,0),B(1-a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是( )
A.4 B.5 C.6 D.10
二、填空题(每小题3分,共18分)
11.已知⊙O的半径为3cm,圆心O到直线l的距离是2cm,则直线l与⊙O的位置关系是___________
12.如图,AB是⊙O的弦,AC是⊙O的切线,切点为A,OC交O0于D,若∠B=35°,则∠C的度数是_________
13.如图,PA,PB分别切⊙O于点A,B,点E是⊙O上一点,且∠AEB=60°,则∠P的度数是_____
14.△ABC中,∠ACB=90°,BC=5,△ABC的内切圆半径为2,则AB的长为_______
15.如图,△ABC的外心的坐标是__________
16.如图,△ABC中,BC=5,AB=7,AC=8,则△ABC的内切圆的面积为________
三、解答题(共8题,共72分)
17.(本题8分)已知矩形ABCD的边AB=3厘米,AD=4厘米,以点A为圆心,3厘米为半径作⊙A,则点B,C,D与⊙A的位置关系如何?请说明理由。
18. (本题8分)如图,在Rt△ABC中,∠B=90°,点O在边AB上,以点O为圆心,⊙A为半径的圆经过点C,过点C作直线MN,使∠BCM=2∠A,判断直线MN与⊙O的位置关系,并说明理由。
19. (本题8分)如图,点M在第一象限内,MN⊥x轴于点N,MN=1,OM与x轴交于A(2,0),B(6,0)两点.
(1)求⊙M的半径的长;
(2)请判断⊙M与直线x=7的位置关系,并说明理由.
20.(本题8分)如图,以□ABCD的一边AB为直径的⊙O恰好与CD相切于点D。
(1)求∠BCD的度数;
(2)连接OC,若AD=4,求OC的长.
21.(本题8分)如图,在△ABC中,AB=AC=10,BC=12,I为△ABC的内心.
(1)求S△ABC;
(2)求BI的长.
22.(本题10分)如图,在Rt△ABC中,∠BAC=90°,O是AB边上的一点,以OA为半径的⊙O与边BC相切于点E。
(1)若AC=5,BC=13,求⊙O的半径长;
(2)过点E作弦EF⊥AB于M,连接AF,若∠F=2∠B,求证:四边形ACEF是菱形.
23.如图,△ABC中,AB=AC,⊙O为△ABC的外接圆,D为⊙O外一点,∠DCA=∠ACB。
(1)求证:CD是⊙O的切线;
(2)连接OD,交AC于点F,若OD⊥AC,当BC=8,⊙O的半径为5时,求CD的长。
24.(本题12分)如图,⊙O为△ABD的外接圆,E为△ABD的内心,DE的延长线交⊙O于点C。
(1)如图1,求证:CE=AC;
(2)如图2,AB为⊙O的直径,AB=10,AD=8。
①求S△ADE;
②求的值。
16.九年级数学(上)第24章《圆》周练(二)
(考试范围:第24.2—点和圆的位置关系;点和圆的位置关系参考时间:90分钟满分:120分)
一、选择题(每小题3分,共30分)
1.已知⊙O的半径为5cm,点P到圆心O的距离为4cm,则点P与⊙O的位置关系是( C )
A.点P在⊙O外 B.点P在⊙O上
C.点P在⊙O内 D.无法判断
2.⊙O的直径为10,圆心O到直线l的距离为5,则直线l与⊙O的位置关系是( B )
A.相交 B.相切 C.相离 D.无法确定
3.如图,PA是⊙O的切线,切点为A,,∠APO=30°,则⊙O的半径为( D)
A.1 B. C.2 D.4
4.如图,AB为⊙O的直径,圆周角∠ABC=20°,当∠BCD=( D )时,CD为⊙O的切线.
A.40° B.50° C.60° D.70°
5.如图,PA,PB是⊙O的切线,A,B为切点,若∠BOA=130°,则∠P的度数是( B )
A.35° B.50° C.55° D.65°
6.如图,PA,PB切⊙O于A,B两点,AC是⊙O的直径,∠P=50°,则∠ACB的度数为( B )
A.50° B.65° C.70° D.80°
7.如图,OI是△ABC的内切圆,D,E,F为三个切点,若∠DEF=50°,则∠A的度数为( B )
A.70° B.80° C.50° D.40°
8.如图,⊙I是△ABC的内切圆,点D,E分别在AB,AC上,且DE是⊙I的切线,若△ADE的周长为9,BC=6,则△ABC的周长是( C )
A.15 B.18 C.21 D.24
9.如图,△ABC中,∠ACB=90°,⊙O为△ABC的内切圆,切点分别为D,E,F,若AD=10,BC=5,则OA的长为( D )
A.8 B.
解:连OE,OF,设⊙O的半径为R,则(10+R)2+52=(15-R)2,R=2。
10.如图,点A(1,0),B(1-a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是( C )
A.4 B.5 C.6 D.10
解:∵A(1,0),B(1-a,0) ,C(1+a,0)(a>0),.AB=1-(1-a)=a,CA=a+1-1=a,
∴AB=AC,∵∠BPC=90°,∴PA=AB=AC=a,延长AD交⊙O于P' ,此时AP'最大,∵A(1,0) ,D(4,4),∴AD=5,∴AP'=5+1=6,.a的最大值为6.
二、填空题(每小题3分,共18分)
11.已知⊙O的半径为3cm,圆心O到直线l的距离是2cm,则直线l与⊙O的位置关系是相交.
12.如图,AB是⊙O的弦,AC是⊙O的切线,切点为A,OC交O0于D,若∠B=35°,则∠C的度数是20°
13.如图,PA,PB分别切⊙O于点A,B,点E是⊙O上一点,且∠AEB=60°,则∠P的度数是60° .
14.△ABC中,∠ACB=90°,BC=5,△ABC的内切圆半径为2,则AB的长为13
15.如图,△ABC的外心的坐标是(-2,-1) .
16.如图,△ABC中,BC=5,AB=7,AC=8,则△ABC的内切圆的面积为3
解:设内切圆的半径为R,过A作AD⊥BC于D,设BD=x,则CD=5-x,由勾股定理得:AB2-BD2=AC2-CD2,即72-x2=8-(5-x)2,解得x=1,AD=,由面积法:BCAD=(AB+BC+AC)R,5×4=20×R,R=,∴S=3。
三、解答题(共8题,共72分)
17. (本题8分)已知矩形ABCD的边AB=3厘米,AD=4厘米,以点A为圆心,3厘米为半径作⊙A,则点B,C,D与⊙A的位置关系如何?请说明理由。
解:点B在⊙A上,点C,D都在⊙A外.
18. (本题8分)如图,在Rt△ABC中,∠B=90°,点O在边AB上,以点O为圆心,⊙A为半径的圆经过点C,过点C作直线MN,使∠BCM=2∠A,判断直线MN与⊙O的位置关系,并说明理由。
解:MN是⊙O切线。理由:连接OC。∵OA=OC,∴∠OAC=∠OCA,∵∠BOC=∠A+∠OCA=2∠A,∠BCM=2∠A,∴∠BCM=∠BOC,∵∠B=90°,∴∠BOC+∠BCO=90°,∴∠BOC+∠BCO=90°,∴OC⊥MN,∴MN是⊙O切线。
19. (本题8分)如图,点M在第一象限内,MN⊥x轴于点N,MN=1,OM与x轴交于A(2,0),B(6,0)两点.
(1)求⊙M的半径的长;
(2)请判断⊙M与直线x=7的位置关系,并说明理由.
解:(1);
(2)易求M(4,1),∴M到x=7的距离d=3>,
∴直线x=7与⊙M相离.
20. (本题8分)如图,以□ABCD的一边AB为直径的⊙O恰好与CD相切于点D。
(1)求∠BCD的度数;
(2)连接OC,若AD=4,求OC的长.
解:(1)连接OD,易证△AOD是等腰直角三角形,
∴∠A=45°=∠BCD;
(2)OA=D=22,CD=AB=4,OC=
21.(本题8分)如图,在△ABC中,AB=AC=10,BC=12,I为△ABC的内心.
(1)求S△ABC;
(2)求BI的长.
解:(1)48;
(2)延长AI交BC于点D,作IE⊥AB于E,则BD=BE=6,AE=4,易求AD=8,设ID=IE=r,则AI=8-r,在△AIE中有:42+r2=(8-r)2,∴r=3,∴BI=。
22.(本题10分)如图,在Rt△ABC中,∠BAC=90°,O是AB边上的一点,以OA为半径的⊙O与边BC相切于点E。
(1)若AC=5,BC=13,求⊙O的半径长;
(2)过点E作弦EF⊥AB于M,连接AF,若∠F=2∠B,求证:四边形ACEF是菱形.
解:(1) CA=CE=5,BE=8,AB=12,设OA=OE=R,OB=12-R,在△OBE中,R2+82= (12一R)2,∴R=;
(2)∵∠AOE=2∠F=4∠B=90°+∠B,∴∠B=30°,∴∠F=60°,∴∠FAB=30°,∴∠FAB=∠B,∴AF//BE,又∵AC// EF,AC=CE,∴四边形ACEF是菱形。
23.如图,△ABC中,AB=AC,⊙O为△ABC的外接圆,D为⊙O外一点,∠DCA=∠ACB。
(1)求证:CD是⊙O的切线;
(2)连接OD,交AC于点F,若OD⊥AC,当BC=8,⊙O的半径为5时,求CD的长。
解:(1)方法一:作直径CM,连接AM,∴∠ACD=∠ACB=∠B=∠M,又∵∠M+∠ACM=90°,∴∠ACD+∠ACM=90°,CD是⊙O的切线;
方法二:连接OC,延长AO交BC于E,∴。∴AE⊥BC,∴∠ACB+∠EAC=90*,∴∠EAC=∠OCA,∴∠ACD+∠OCA=90°,∴CD是⊙O的切线.
(2)延长AO交BC于E,∴AB=AC,∴AE⊥BC,∴BE=CE=4,∴OE=3,∴AE=8,∴AC=,∵OD⊥AC,∵AF=CF=,∴OF=,设DF=x,∴OD2-OC2=CD2=DF2+CF2,∴(x+)2-52=x2+(2)2,x=,∴CD==10。
24.(本题12分)如图,⊙O为△ABD的外接圆,E为△ABD的内心,DE的延长线交⊙O于点C。
(1)如图1,求证:CE=AC;
(2)如图2,AB为⊙O的直径,AB=10,AD=8。
①求S△ADE;
②求的值。
解:(1)连AE,证∠CAE=∠CEA即可。
(2)①作EF⊥AD于F,作EG⊥AB于G,则EF,EG为△ADB内切圆心的半径,∴2DF=AD+BD-AB,∴DF=2=EF,∴S△ADE=ADEF=8。
②∵EF=DF=2,∴AF=AG=6,∴AE==2,由(1)知CE=AC=AB=5,∴=2
21世纪教育网(www.21cnjy.com)
同课章节目录
