九年级数学(上)第24章《圆》周练(三)(含答案)
文档属性
| 名称 | 九年级数学(上)第24章《圆》周练(三)(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 592.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-18 19:23:31 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
17.九年级数学(上)第24章《圆》周练(三)
一、选择题(每小题3分,共30分)
1.正八边形的每个内角为( )
A.120° B.135° C.140° D.144°
2.下列正多边形中,既是轴对称图形,又是中心对称图形的是( ).
A.正三角形 B.正方形 C.正五边形 D.正七边形
3.正五边形的中心角为( )
A.108° B.90° C.72° D.60°
4.如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠ABC=120°,OC=3,则BC的长为( )
A. B.2 C.3 D.5
第4题图 第5题图 第8题图 第9题图 第10题图
5.如图,正六边形ABCDEF中,AB=2,点P是ED的中点,连接AP,则AP的长为( )
A. B.4 C. D.
6.用一个圆心角为120°,半径为3的扇形作一个圆锥的侧面,则这个圆锥的底面半径为( ).
A. B.1 C. D.2
7.一个圆锥的侧面积是底面积的2倍,则该圆锥的側面展开图的扇形圆心角等于( ) .
A.90° B.120°C.150°D.180°
8.如图,已知⊙O的半径为13,弦AB=10,CD=24,则图中阴影部分的面积是( ).
A. B. C. D.不能确定
9.蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,△ABC的顶点都在格点上.设定AB边如图所示,则△ABC是直角三角形的个数有( ).
A.4个 B.6个 C.8个D.10个
10.如图,点A,B,C为⊙O上三点,∠A=60°,BC=4,点D为BC上一动点,BE⊥OD交直线OD于E,当点D由点B出发,沿BC运动到点C时,点E经过的路径长为( ).
A. B. C. D.6
二、填空题(每题3分,共18分)
11.若一个正多边形的每个内角的度数是中心角的3倍,则正多边形的边数是 .
12.一个扇形的半径为8cm,弧长为则扇形的圆心角为 .
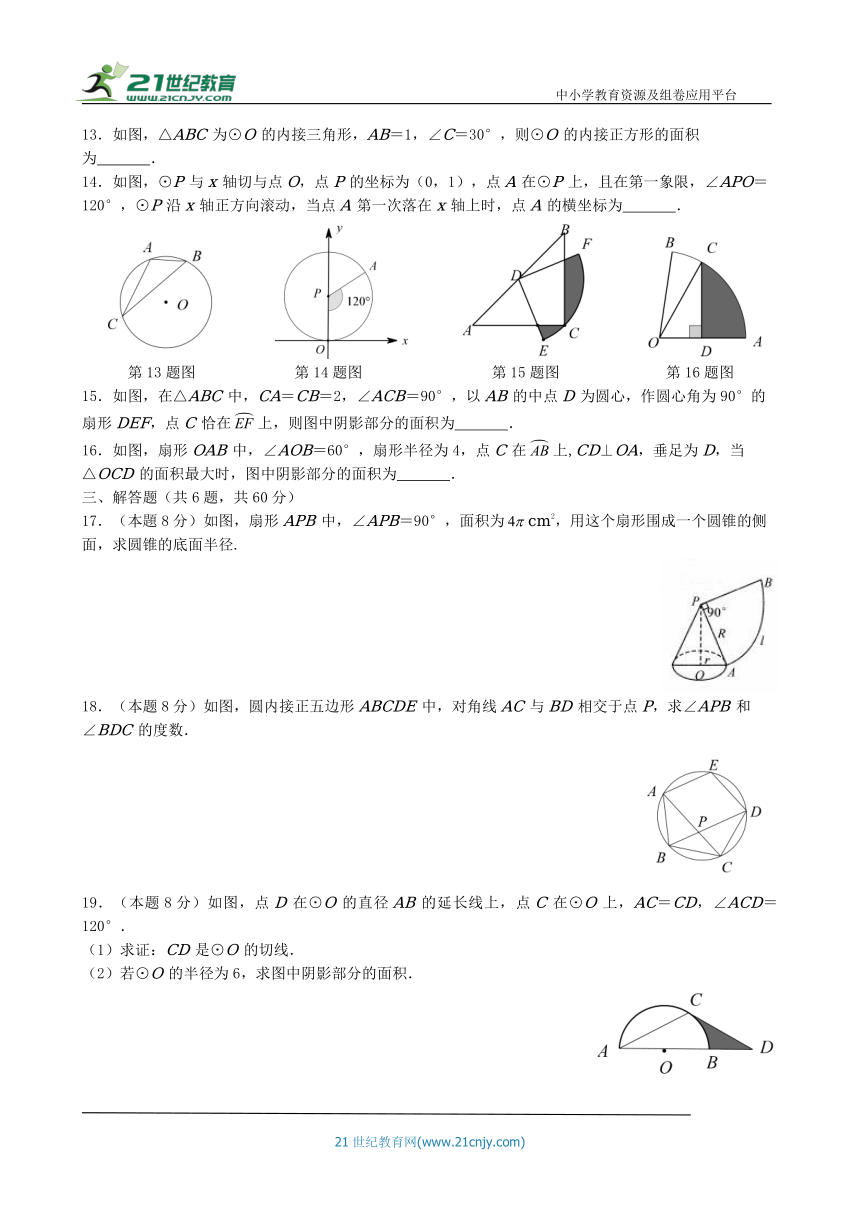
13.如图,△ABC为⊙O的内接三角形,AB=1,∠C=30°,则⊙O的内接正方形的面积为 .
14.如图,⊙P与x轴切与点O,点P的坐标为(0,1),点A在⊙P上,且在第一象限,∠APO=120°,⊙P沿x轴正方向滚动,当点A第一次落在x轴上时,点A的横坐标为 .
第13题图 第14题图 第15题图 第16题图
15.如图,在△ABC中,CA=CB=2,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在上,则图中阴影部分的面积为 .
16.如图,扇形OAB中,∠AOB=60°,扇形半径为4,点C在上,CD⊥OA,垂足为D,当△OCD的面积最大时,图中阴影部分的面积为 .
三、解答题(共6题,共60分)
17.(本題8分)如图,扇形APB中,∠APB=90°,面积为cm2,用这个扇形围成一个圆锥的侧面,求圆锥的底面半径.
18.(本题8分)如图,圆内接正五边形ABCDE中,对角线AC与BD相交于点P,求∠APB和∠BDC的度数.
19.(本题8分)如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线.
(2)若⊙O的半径为6,求图中阴影部分的面积.
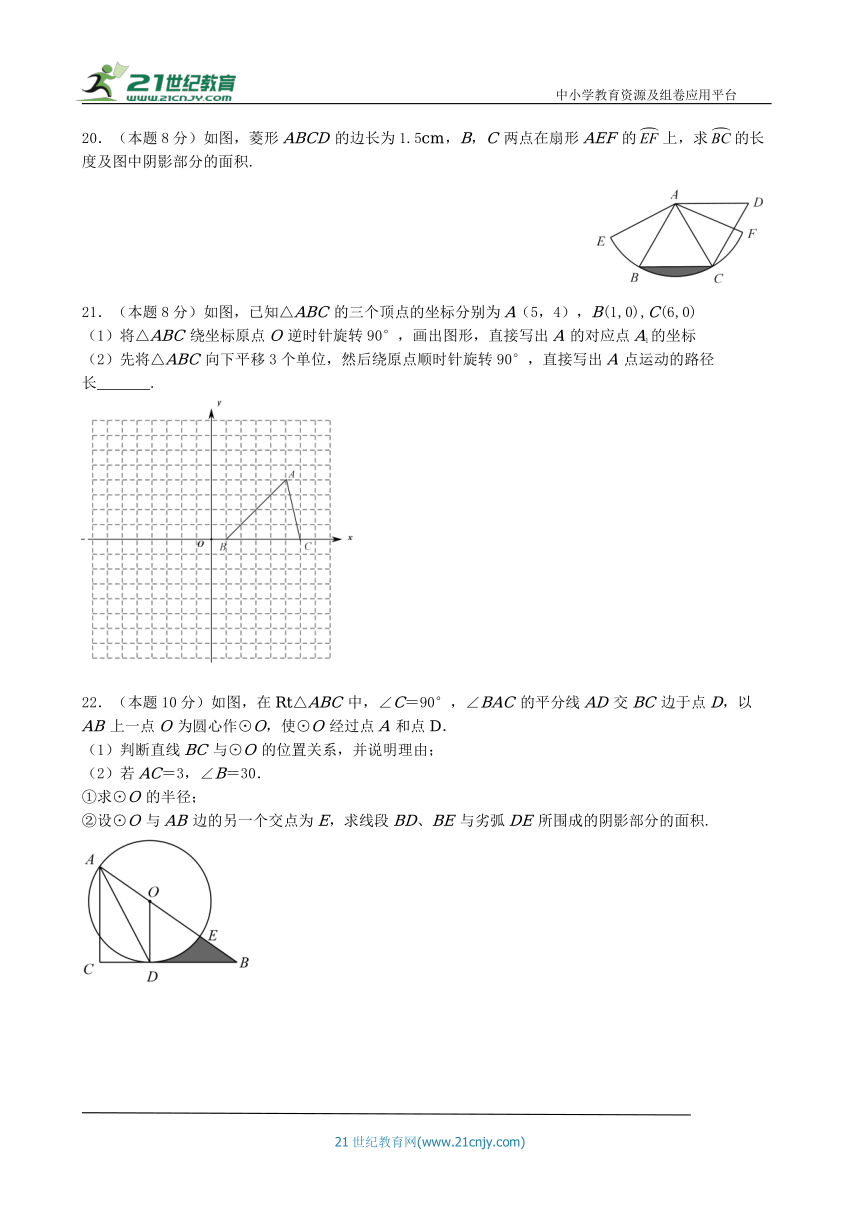
20.(本题8分)如图,菱形ABCD的边长为1.5cm,B,C两点在扇形AEF的上,求的长度及图中阴影部分的面积.
21.(本题8分)如图,已知△ABC的三个顶点的坐标分别为A(5,4),B(1,0),C(6,0)
(1)将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出A的对应点A1的坐标
(2)先将△ABC向下平移3个单位,然后绕原点顺时针旋转90°,直接写出A点运动的路径长 .
22.(本题10分)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D,以AB上一点O为圆心作⊙O,使⊙O经过点A和点D.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AC=3,∠B=30.
①求⊙O的半径;
②设⊙O与AB边的另一个交点为E,求线段BD、BE与劣弧DE所围成的阴影部分的面积.
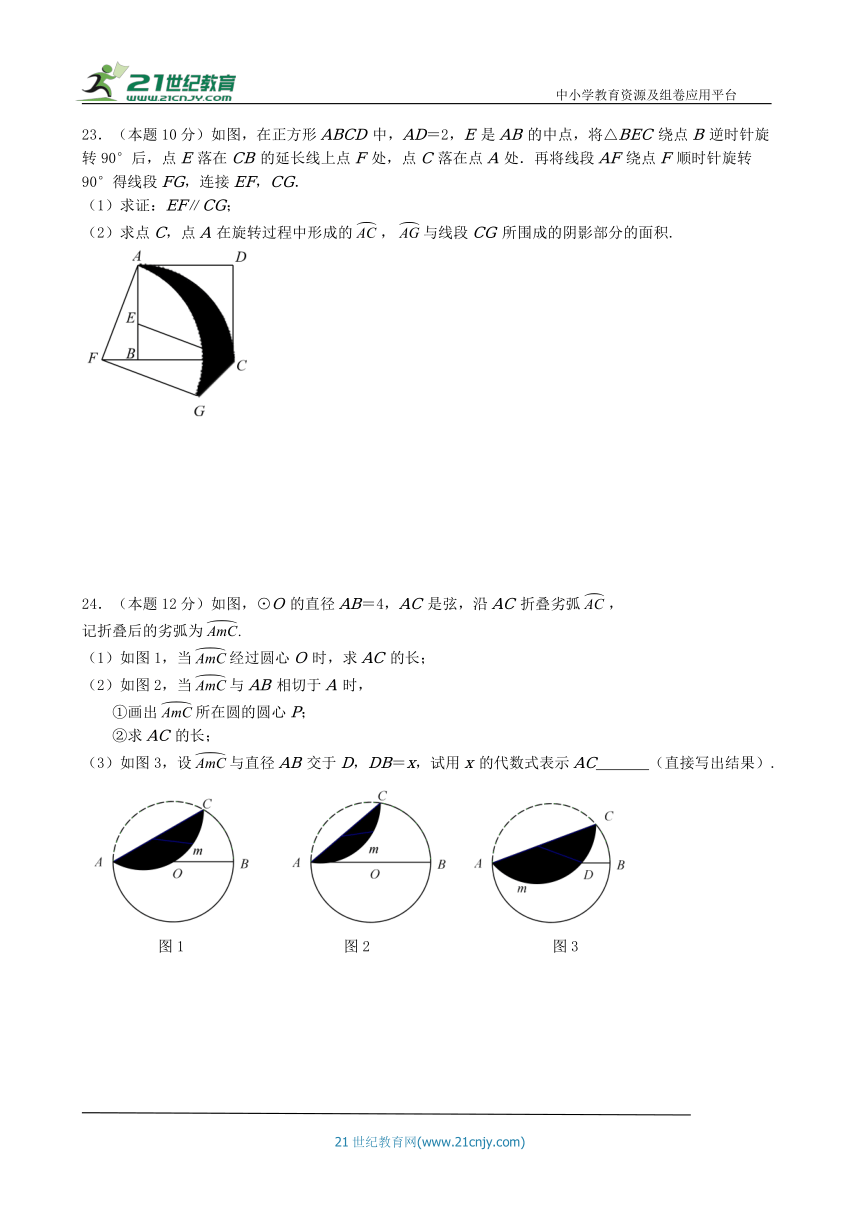
23.(本题10分)如图,在正方形ABCD中,AD=2,E是AB的中点,将△BEC绕点B逆时针旋转90°后,点E落在CB的延长线上点F处,点C落在点A处.再将线段AF绕点F顺时针旋转90°得线段FG,连接EF,CG.
(1)求证:EF∥CG;
(2)求点C,点A在旋转过程中形成的,与线段CG所围成的阴影部分的面积.
24.(本题12分)如图,⊙O的直径AB=4,AC是弦,沿AC折叠劣弧,
记折叠后的劣弧为
(1)如图1,当经过圆心O时,求AC的长;
(2)如图2,当与AB相切于A时,
①画出所在圆的圆心P;
②求AC的长;
(3)如图3,设与直径AB交于D,DB=x,试用x的代数式表示AC (直接写出结果).
图1 图2 图3
17.九年级数学(上)第24章《圆》周练(三)
一、选择题(每小题3分,共30分)
1.正八边形的每个内角为( B )
A.120° B.135° C.140° D.144°
2.下列正多边形中,既是轴对称图形,又是中心对称图形的是( B ).
A.正三角形 B.正方形 C.正五边形 D.正七边形
3.正五边形的中心角为( C )
A.108° B.90° C.72° D.60°
4.如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠ABC=120°,OC=3,则BC的长为( B )
A. B.2 C.3 D.5
第4题图 第5题图 第8题图 第9题图 第10题图
5.如图,正六边形ABCDEF中,AB=2,点P是ED的中点,连接AP,则AP的长为( C )
A. B.4 C. D.
6.用一个圆心角为120°,半径为3的扇形作一个圆锥的侧面,则这个圆锥的底面半径为( B ).
A. B.1 C. D.2
7.一个圆锥的侧面积是底面积的2倍,则该圆锥的側面展开图的扇形圆心角等于( D ) .
A.90° B.120°C.150°D.180°
8.如图,已知⊙O的半径为13,弦AB=10,CD=24,则图中阴影部分的面积是( C ).
A. B. C. D.不能确定
9.蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,△ABC的顶点都在格点上.设定AB边如图所示,则△ABC是直角三角形的个数
有( D ).
A.4个 B.6个 C.8个D.10个
10.如图,点A,B,C为⊙O上三点,∠A=60°,BC=4,点D为BC上一动点,BE⊥OD交直线OD于E,当点D由点B出发,沿BC运动到点C时,点E经过的路径长为( B ).
A. B. C. D.6
解:E点应在以OB为直径的圆上,故E点所经过的路径为弧长,当D点运动到
C点时,其弧所对圆心角为240°,其直径为OB,连接OC,作OH⊥BC于H,
可求OB=
二、填空题(每题3分,共18分)
11.若一个正多边形的每个内角的度数是中心角的3倍,则正多边形的边数是8.
12.一个扇形的半径为8cm,弧长为则扇形的圆心角为120°.
13.如图,△ABC为⊙O的内接三角形,AB=1,∠C=30°,则⊙O的内接正方形的面积为2.
14.如图,⊙P与x轴切与点O,点P的坐标为(0,1),点A在⊙P上,且在第一象限,∠APO=120°,⊙P沿x轴正方向滚动,当点A第一次落在x轴上时,点A的横坐标为.
第13题图 第14题图 第15题图 第16题图
15.如图,在△ABC中,CA=CB=2,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在上,则图中阴影部分的面积为.
[解析]S影=S扇DBC-S△DBC.
16.如图,扇形OAB中,∠AOB=60°,扇形半径为4,点C在上,CD⊥OA,垂足为D,当△OCD的面积最大时,图中阴影部分的面积为.
解:
三、解答题(共6题,共60分)
17.(本題8分)如图,扇形APB中,∠APB=90°,面积为cm2,用这个扇形围成一个圆锥的侧面,求圆锥的底面半径.
解:设这个圆的底面半径为r,扇形半径为R,则
即这个圆锥的底半径为1cm.
18.(本题8分)如图,圆内接正五边形ABCDE中,对角线AC与BD相交于点P,求∠APB和∠BDC的度数.
解:计算正五边形的内角为108°,∠APB=72°,∠BDC=36°
19.(本题8分)如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线.
(2)若⊙O的半径为6,求图中阴影部分的面积.
解:(1)略;(2)
20.(本题8分)如图,菱形ABCD的边长为1.5cm,B,C两点在扇形AEF的上,求的长度及图中阴影部分的面积.
解:四边形ABCD是菱形且边长为1.5 ,∴AB=BC=1.5.
又∵B、C两点在扇形AEF的上 ∴AB=BC=AC=1.5,
∴△ABC是等边三角形,∴∠BAC=60°,
的长=
易求S△ABC
21.(本题8分)如图,已知△ABC的三个顶点的坐标分别为A(5,4),B(1,0),C(6,0)
(1)将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出A的对应点A1的坐标
(2)先将△ABC向下平移3个单位,然后绕原点顺时针旋转90°,直接写出A点运动的路径长 .
解:(1)A1(-4,5),
(2)
22.(本题10分)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D,以AB上一点O为圆心作⊙O,使⊙O经过点A和点D.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AC=3,∠B=30.
①求⊙O的半径;
②设⊙O与AB边的另一个交点为E,求线段BD、BE与劣弧DE所围成的阴影部分的面积.
解:(1)略;(2)①2;②
23.(本题10分)如图,在正方形ABCD中,AD=2,E是AB的中点,将△BEC绕点B逆时针旋转90°后,点E落在CB的延长线上点F处,点C落在点A处.再将线段AF绕点F顺时针旋转90°得线段FG,连接EF,CG.
(1)求证:EF∥CG;
(2)求点C,点A在旋转过程中形成的,与线段CG所围成的阴影部分的面积.
解:(1)证∠FAB=∠ECB,∠FAB=∠CFG,∴∠ECB=∠CFG,CE∥FG.
又∵CE=AF=FG,∴CE∥FG且CE=FG,
∴四EFGC是平行四边形,∴EF∥CG.
(2)易求AE=BE=BF=1,AF=FG=,△EFC≌△CCF,
∴S影=S扇BAC+S△ABF+S△CFG-S△FAG=
24.(本题12分)如图,⊙O的直径AB=4,AC是弦,沿AC折叠劣弧,
记折叠后的劣弧为
(1)如图1,当经过圆心O时,求AC的长;
(2)如图2,当与AB相切于A时,
①画出所在圆的圆心P;
②求AC的长;
(4)如图3,设与直径AB交于D,DB=x,试用x的代数式表示AC (直接写出结果).
图1 图2 图3
解:(1)作半径OE⊥AC于F,
∴OF=OE=OA=1,∴∠FAO=30°,
∴AC=2AF=
(2)①作出圆心P(方法不限);②连PC、PA、CO、
∵PC=PA=OC=OA=2,
∴四边形PAOC是菱形.因为弧AmC切AB于A,∴PA⊥AB,
∴菱形PAOC的正方形 ∴AC=
(3)AC=
21世纪教育网(www.21cnjy.com)
17.九年级数学(上)第24章《圆》周练(三)
一、选择题(每小题3分,共30分)
1.正八边形的每个内角为( )
A.120° B.135° C.140° D.144°
2.下列正多边形中,既是轴对称图形,又是中心对称图形的是( ).
A.正三角形 B.正方形 C.正五边形 D.正七边形
3.正五边形的中心角为( )
A.108° B.90° C.72° D.60°
4.如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠ABC=120°,OC=3,则BC的长为( )
A. B.2 C.3 D.5
第4题图 第5题图 第8题图 第9题图 第10题图
5.如图,正六边形ABCDEF中,AB=2,点P是ED的中点,连接AP,则AP的长为( )
A. B.4 C. D.
6.用一个圆心角为120°,半径为3的扇形作一个圆锥的侧面,则这个圆锥的底面半径为( ).
A. B.1 C. D.2
7.一个圆锥的侧面积是底面积的2倍,则该圆锥的側面展开图的扇形圆心角等于( ) .
A.90° B.120°C.150°D.180°
8.如图,已知⊙O的半径为13,弦AB=10,CD=24,则图中阴影部分的面积是( ).
A. B. C. D.不能确定
9.蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,△ABC的顶点都在格点上.设定AB边如图所示,则△ABC是直角三角形的个数有( ).
A.4个 B.6个 C.8个D.10个
10.如图,点A,B,C为⊙O上三点,∠A=60°,BC=4,点D为BC上一动点,BE⊥OD交直线OD于E,当点D由点B出发,沿BC运动到点C时,点E经过的路径长为( ).
A. B. C. D.6
二、填空题(每题3分,共18分)
11.若一个正多边形的每个内角的度数是中心角的3倍,则正多边形的边数是 .
12.一个扇形的半径为8cm,弧长为则扇形的圆心角为 .
13.如图,△ABC为⊙O的内接三角形,AB=1,∠C=30°,则⊙O的内接正方形的面积为 .
14.如图,⊙P与x轴切与点O,点P的坐标为(0,1),点A在⊙P上,且在第一象限,∠APO=120°,⊙P沿x轴正方向滚动,当点A第一次落在x轴上时,点A的横坐标为 .
第13题图 第14题图 第15题图 第16题图
15.如图,在△ABC中,CA=CB=2,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在上,则图中阴影部分的面积为 .
16.如图,扇形OAB中,∠AOB=60°,扇形半径为4,点C在上,CD⊥OA,垂足为D,当△OCD的面积最大时,图中阴影部分的面积为 .
三、解答题(共6题,共60分)
17.(本題8分)如图,扇形APB中,∠APB=90°,面积为cm2,用这个扇形围成一个圆锥的侧面,求圆锥的底面半径.
18.(本题8分)如图,圆内接正五边形ABCDE中,对角线AC与BD相交于点P,求∠APB和∠BDC的度数.
19.(本题8分)如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线.
(2)若⊙O的半径为6,求图中阴影部分的面积.
20.(本题8分)如图,菱形ABCD的边长为1.5cm,B,C两点在扇形AEF的上,求的长度及图中阴影部分的面积.
21.(本题8分)如图,已知△ABC的三个顶点的坐标分别为A(5,4),B(1,0),C(6,0)
(1)将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出A的对应点A1的坐标
(2)先将△ABC向下平移3个单位,然后绕原点顺时针旋转90°,直接写出A点运动的路径长 .
22.(本题10分)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D,以AB上一点O为圆心作⊙O,使⊙O经过点A和点D.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AC=3,∠B=30.
①求⊙O的半径;
②设⊙O与AB边的另一个交点为E,求线段BD、BE与劣弧DE所围成的阴影部分的面积.
23.(本题10分)如图,在正方形ABCD中,AD=2,E是AB的中点,将△BEC绕点B逆时针旋转90°后,点E落在CB的延长线上点F处,点C落在点A处.再将线段AF绕点F顺时针旋转90°得线段FG,连接EF,CG.
(1)求证:EF∥CG;
(2)求点C,点A在旋转过程中形成的,与线段CG所围成的阴影部分的面积.
24.(本题12分)如图,⊙O的直径AB=4,AC是弦,沿AC折叠劣弧,
记折叠后的劣弧为
(1)如图1,当经过圆心O时,求AC的长;
(2)如图2,当与AB相切于A时,
①画出所在圆的圆心P;
②求AC的长;
(3)如图3,设与直径AB交于D,DB=x,试用x的代数式表示AC (直接写出结果).
图1 图2 图3
17.九年级数学(上)第24章《圆》周练(三)
一、选择题(每小题3分,共30分)
1.正八边形的每个内角为( B )
A.120° B.135° C.140° D.144°
2.下列正多边形中,既是轴对称图形,又是中心对称图形的是( B ).
A.正三角形 B.正方形 C.正五边形 D.正七边形
3.正五边形的中心角为( C )
A.108° B.90° C.72° D.60°
4.如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠ABC=120°,OC=3,则BC的长为( B )
A. B.2 C.3 D.5
第4题图 第5题图 第8题图 第9题图 第10题图
5.如图,正六边形ABCDEF中,AB=2,点P是ED的中点,连接AP,则AP的长为( C )
A. B.4 C. D.
6.用一个圆心角为120°,半径为3的扇形作一个圆锥的侧面,则这个圆锥的底面半径为( B ).
A. B.1 C. D.2
7.一个圆锥的侧面积是底面积的2倍,则该圆锥的側面展开图的扇形圆心角等于( D ) .
A.90° B.120°C.150°D.180°
8.如图,已知⊙O的半径为13,弦AB=10,CD=24,则图中阴影部分的面积是( C ).
A. B. C. D.不能确定
9.蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,△ABC的顶点都在格点上.设定AB边如图所示,则△ABC是直角三角形的个数
有( D ).
A.4个 B.6个 C.8个D.10个
10.如图,点A,B,C为⊙O上三点,∠A=60°,BC=4,点D为BC上一动点,BE⊥OD交直线OD于E,当点D由点B出发,沿BC运动到点C时,点E经过的路径长为( B ).
A. B. C. D.6
解:E点应在以OB为直径的圆上,故E点所经过的路径为弧长,当D点运动到
C点时,其弧所对圆心角为240°,其直径为OB,连接OC,作OH⊥BC于H,
可求OB=
二、填空题(每题3分,共18分)
11.若一个正多边形的每个内角的度数是中心角的3倍,则正多边形的边数是8.
12.一个扇形的半径为8cm,弧长为则扇形的圆心角为120°.
13.如图,△ABC为⊙O的内接三角形,AB=1,∠C=30°,则⊙O的内接正方形的面积为2.
14.如图,⊙P与x轴切与点O,点P的坐标为(0,1),点A在⊙P上,且在第一象限,∠APO=120°,⊙P沿x轴正方向滚动,当点A第一次落在x轴上时,点A的横坐标为.
第13题图 第14题图 第15题图 第16题图
15.如图,在△ABC中,CA=CB=2,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在上,则图中阴影部分的面积为.
[解析]S影=S扇DBC-S△DBC.
16.如图,扇形OAB中,∠AOB=60°,扇形半径为4,点C在上,CD⊥OA,垂足为D,当△OCD的面积最大时,图中阴影部分的面积为.
解:
三、解答题(共6题,共60分)
17.(本題8分)如图,扇形APB中,∠APB=90°,面积为cm2,用这个扇形围成一个圆锥的侧面,求圆锥的底面半径.
解:设这个圆的底面半径为r,扇形半径为R,则
即这个圆锥的底半径为1cm.
18.(本题8分)如图,圆内接正五边形ABCDE中,对角线AC与BD相交于点P,求∠APB和∠BDC的度数.
解:计算正五边形的内角为108°,∠APB=72°,∠BDC=36°
19.(本题8分)如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线.
(2)若⊙O的半径为6,求图中阴影部分的面积.
解:(1)略;(2)
20.(本题8分)如图,菱形ABCD的边长为1.5cm,B,C两点在扇形AEF的上,求的长度及图中阴影部分的面积.
解:四边形ABCD是菱形且边长为1.5 ,∴AB=BC=1.5.
又∵B、C两点在扇形AEF的上 ∴AB=BC=AC=1.5,
∴△ABC是等边三角形,∴∠BAC=60°,
的长=
易求S△ABC
21.(本题8分)如图,已知△ABC的三个顶点的坐标分别为A(5,4),B(1,0),C(6,0)
(1)将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出A的对应点A1的坐标
(2)先将△ABC向下平移3个单位,然后绕原点顺时针旋转90°,直接写出A点运动的路径长 .
解:(1)A1(-4,5),
(2)
22.(本题10分)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D,以AB上一点O为圆心作⊙O,使⊙O经过点A和点D.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AC=3,∠B=30.
①求⊙O的半径;
②设⊙O与AB边的另一个交点为E,求线段BD、BE与劣弧DE所围成的阴影部分的面积.
解:(1)略;(2)①2;②
23.(本题10分)如图,在正方形ABCD中,AD=2,E是AB的中点,将△BEC绕点B逆时针旋转90°后,点E落在CB的延长线上点F处,点C落在点A处.再将线段AF绕点F顺时针旋转90°得线段FG,连接EF,CG.
(1)求证:EF∥CG;
(2)求点C,点A在旋转过程中形成的,与线段CG所围成的阴影部分的面积.
解:(1)证∠FAB=∠ECB,∠FAB=∠CFG,∴∠ECB=∠CFG,CE∥FG.
又∵CE=AF=FG,∴CE∥FG且CE=FG,
∴四EFGC是平行四边形,∴EF∥CG.
(2)易求AE=BE=BF=1,AF=FG=,△EFC≌△CCF,
∴S影=S扇BAC+S△ABF+S△CFG-S△FAG=
24.(本题12分)如图,⊙O的直径AB=4,AC是弦,沿AC折叠劣弧,
记折叠后的劣弧为
(1)如图1,当经过圆心O时,求AC的长;
(2)如图2,当与AB相切于A时,
①画出所在圆的圆心P;
②求AC的长;
(4)如图3,设与直径AB交于D,DB=x,试用x的代数式表示AC (直接写出结果).
图1 图2 图3
解:(1)作半径OE⊥AC于F,
∴OF=OE=OA=1,∴∠FAO=30°,
∴AC=2AF=
(2)①作出圆心P(方法不限);②连PC、PA、CO、
∵PC=PA=OC=OA=2,
∴四边形PAOC是菱形.因为弧AmC切AB于A,∴PA⊥AB,
∴菱形PAOC的正方形 ∴AC=
(3)AC=
21世纪教育网(www.21cnjy.com)
同课章节目录
