九年级数学(上)第24章《圆》专题卷B——核心思想方法归纳一点通(选用)(含答案)
文档属性
| 名称 | 九年级数学(上)第24章《圆》专题卷B——核心思想方法归纳一点通(选用)(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 374.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-18 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
19.九年级数学(上)第24章《圆》专题卷B 核心思想方法归纳一点通(选用)
一、常见基本图形和基本结论梳理(不含相似及三角函数)
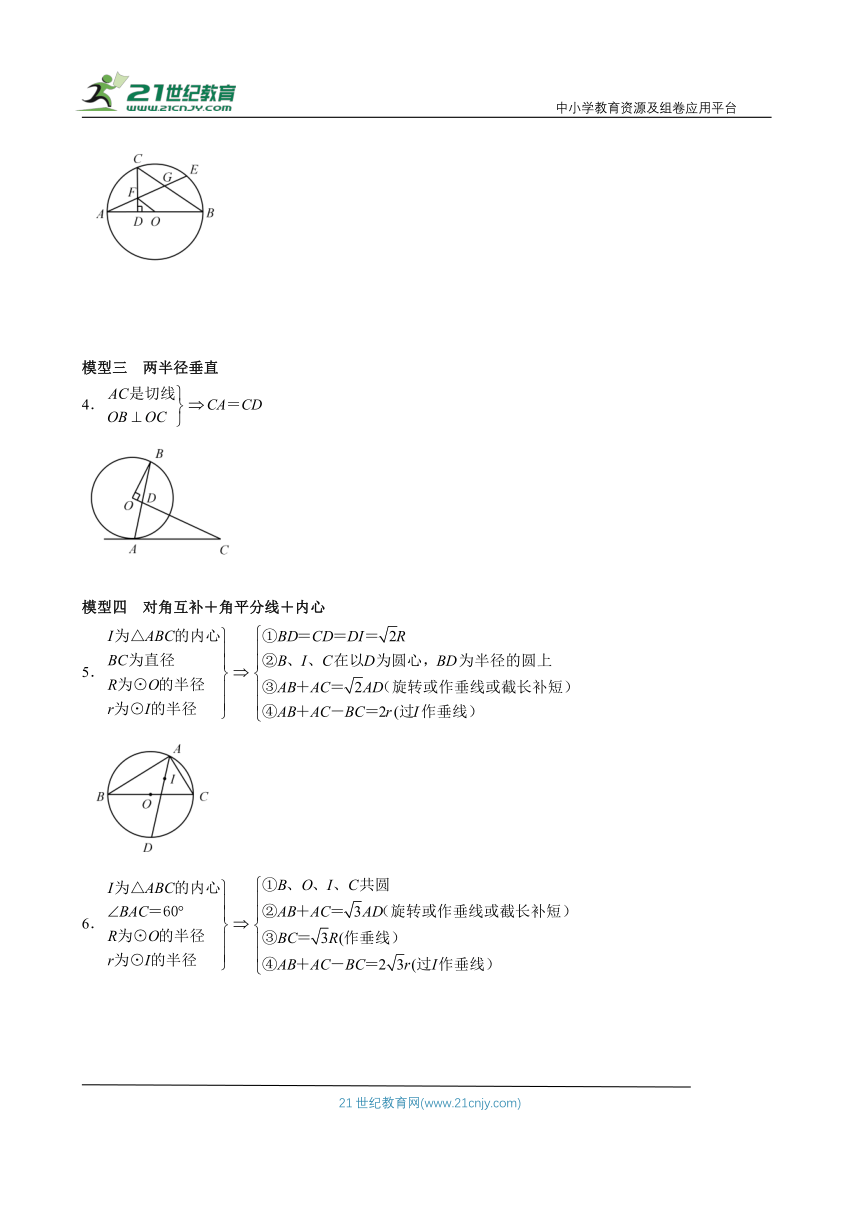
模型一 两弦垂直
1.
模型二 直径垂直于弦
2.直径AB⊥CD
3.
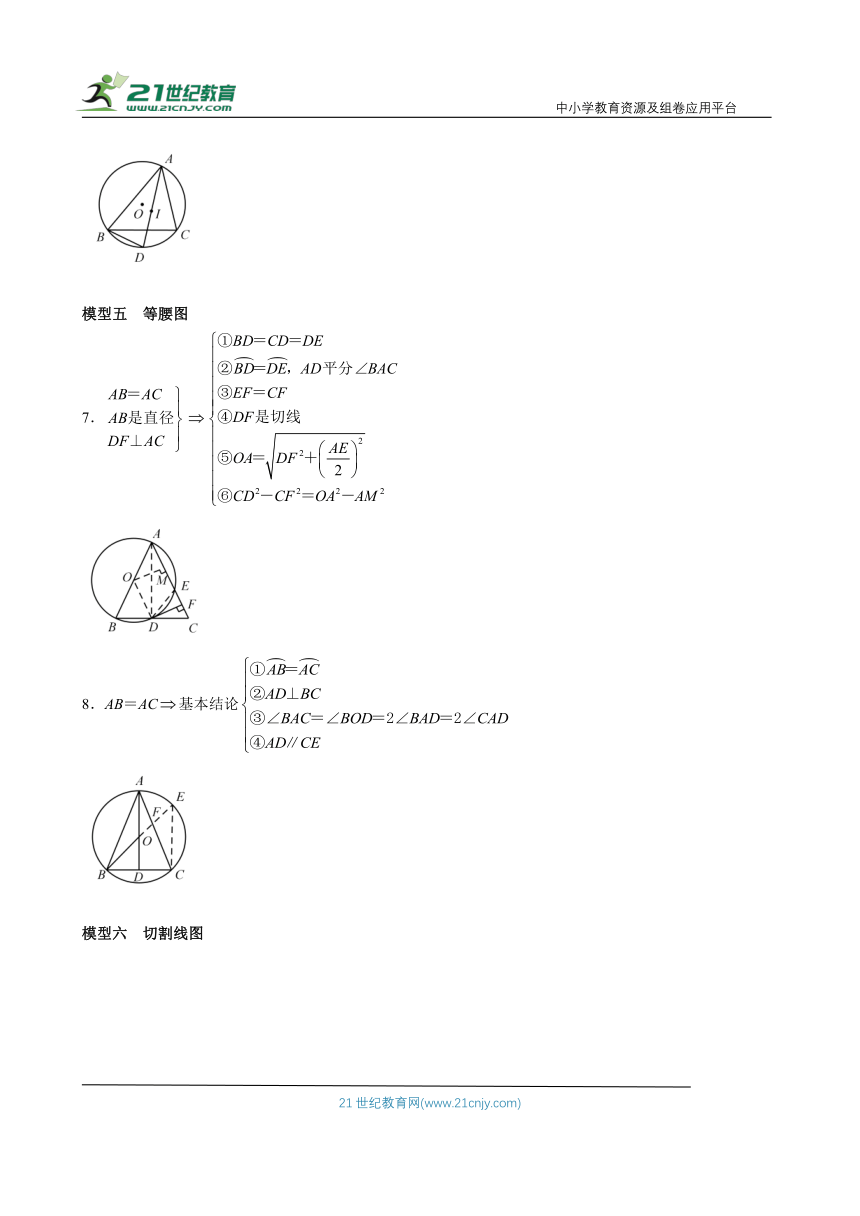
模型三 两半径垂直
4.CA=CD
模型四 对角互补+角平分线+内心
5.
6.
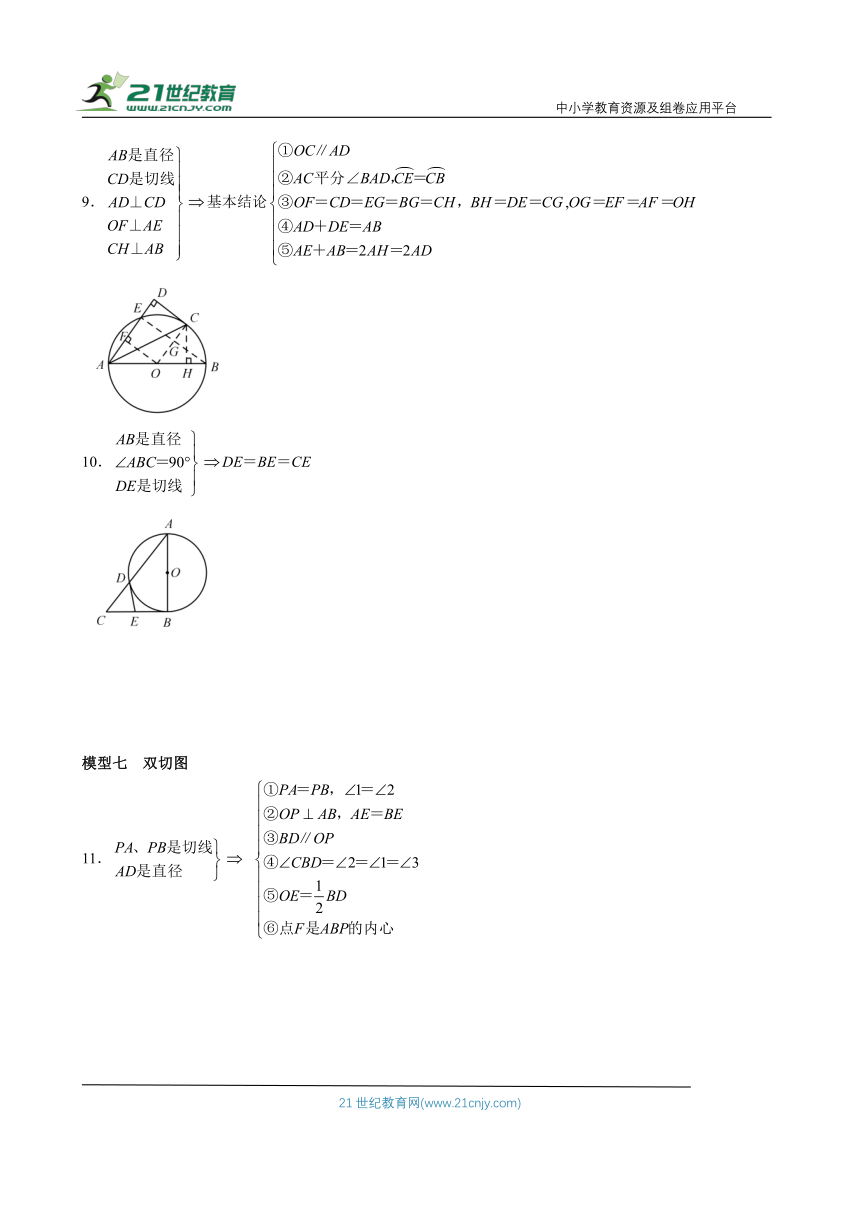
模型五 等腰图
7.
8.AB=AC基本结论
模型六 切割线图
9.基本结论
10.DE=BE=CE
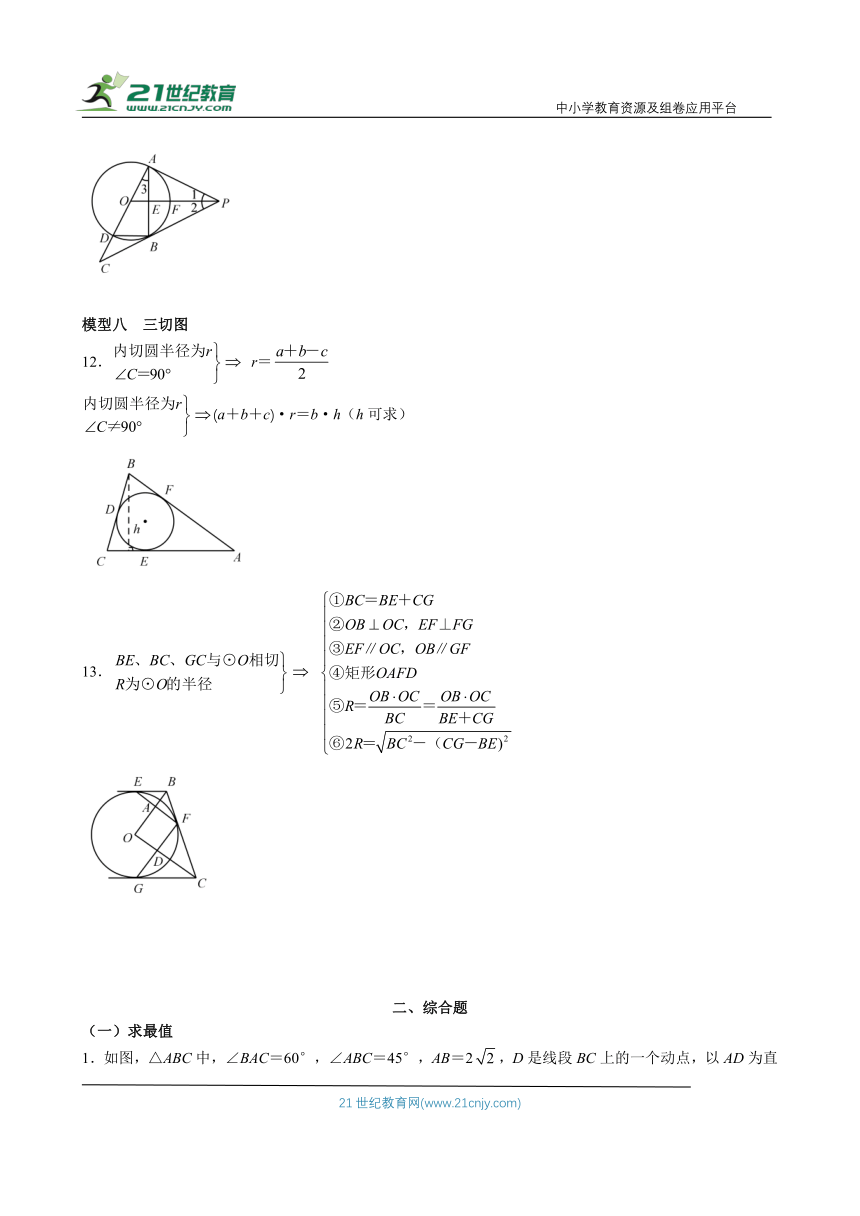
模型七 双切图
11.
模型八 三切图
12. r=
(a+b+c)·r=b·h(h可求)
13.
二、综合题
(一)求最值
1.如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=2,D是线段BC上的一个动点,以AD为直径的⊙O分别交AB、AC于E、F,连接EF,则线段EF的最小值为 .
2.如图,⊙O的半径为2,弦AB的长为2,点P为优弧上一动点,AC⊥AP交直线PB于点C,则△ABC的面积的最大值是( )
A.12+6 B.6+3 C.12+3 D.6+4
3.如图,□ABCD中,∠A=60°,AD=3,CD=4,点P是边AB上的动点,将△APD沿PD折叠,点A的对应点为Q,则△BOC面积的最小值为 .
4.如图,P为⊙O内的一个定点, A为⊙O上的一个动点,射线AP、AO分别与⊙O交于B、C两点,若⊙O的半径长为3,OP=,则弦BC的最大值为( )
A.2 B.3 C. D.3
5.如图,△ABC中,AB=4,以AB为直径的⊙O分别交BC、AC于D、E,若∠DOE=60°,则CD的最大值为 .
(二)求路径长
6.如图, AB为⊙O的直径,C为半圆上一点,∠CAB=45°,AC=4,点D在⊙O上,P为CD的中点,当点D沿半圆从点B运动至点A时,点P运动的路径长是 .
7.如图,⊙O的半径为8,圆心角∠AOB=120°,P为上的动点,PE⊥OA于E,PF⊥OB于F,设过P、E、O、F的圆的圆心为O ,当点F从点O开始运动时起,到点E到达点O时止,点O 运动的路径长为 .
8.如图,正方形ABCD的边长为2,E、F分别为AD、CD上一动点,AE=DF,BE、AF交于点M,当点E从点A运动到点D时,点M运动的路径长是 .
9.如图,半径为4的⊙O中,CD为直径,弦AB⊥CD且过半径OD的中点,点E为⊙O上一动点,CF⊥AE于点F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( )
A.π B.π C.π D.π
10.如图,半径为2cm,圆心角为90°的扇形OAB的上有一运动的点P,从点P向半径OA引垂线PH交OA于点H.设△OPH的内心为I,当点P在上从点A运动到点B时,内心I所经过的路径长为 .
(三)证明与计算
11.如图,在⊙O中,=,CD⊥AB于点F,交⊙O于点D,AO的延长线交CD于点E.
(1)求证:AD=AE;
(2)若=,求的值.
12.如图,AB是⊙O的直径,点D是⊙O上一点,BC⊥CD于点C,交⊙O于点E,F是半圆的中点,EF交BD于点G,连接AE、OG.
(1)求证:点G是△ABE的内心;
(2)若BE=6,CD=4,求OG的长.
19.九年级数学(上)第24章《圆》专题卷B 核心思想方法归纳一点通(选用)
一、常见基本图形和基本结论梳理(不含相似及三角函数)
模型一 两弦垂直
1.
模型二 直径垂直于弦
2.直径AB⊥CD
3.
模型三 两半径垂直
4.CA=CD
模型四 对角互补+角平分线+内心
5.
6.
模型五 等腰图
7.
8.AB=AC基本结论
模型六 切割线图
9.基本结论
10.DE=BE=CE
模型七 双切图
11.
模型八 三切图
12. r=
(a+b+c)·r=b·h(h可求)
13.
二、综合题
(一)求最值
1.如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=2,D是线段BC上的一个动点,以AD为直径的⊙O分别交AB、AC于E、F,连接EF,则线段EF的最小值为 .
解:作直径EM,连MF,∠M=60°,EF=EM=AD.要使EF最小,只需使AD最小,故AD⊥BC,∴AD=2,EF=.
2.如图,⊙O的半径为2,弦AB的长为2,点P为优弧上一动点,AC⊥AP交直线PB于点C,则△ABC的面积的最大值是( )
A.12+6 B.6+3 C.12+3 D.6+4
提示:易求∠P=60°,∠C=30°,作△ABC的外接圆⊙O ,当AB边上的高最大,即高过⊙O 的圆心O 时,△ABC的面积最大,此时高垂直平分AB.
3.如图,□ABCD中,∠A=60°,AD=3,CD=4,点P是边AB上的动点,将△APD沿PD折叠,点A的对应点为Q,则△BOC面积的最小值为 .
解:点Q在以D为圆心,DA为半径的圆上运动,过Q作EF∥BC,分别交AB、CD于E、F,当EF与,⊙O相切时,EF与BC之间的距离最小,S△BOC最小为3-.
4.如图,P为⊙O内的一个定点, A为⊙O上的一个动点,射线AP、AO分别与⊙O交于B、C两点,若⊙O的半径长为3,OP=,则弦BC的最大值为( )
A.2 B.3 C. D.3
答案:A
5.如图,△ABC中,AB=4,以AB为直径的⊙O分别交BC、AC于D、E,若∠DOE=60°,则CD的最大值为 .
解:易证∠C=60°,连AD,则∠ADB=90°,∴CD=AC,当AC取最大值时,CD的值最大,作△ABC的外接圆⊙M,当AC为⊙M的直径时,AC最大,∴AC最大=,∴CD的最大值为.
(二)求路径长
6.如图, AB为⊙O的直径,C为半圆上一点,∠CAB=45°,AC=4,点D在⊙O上,P为CD的中点,当点D沿半圆从点B运动至点A时,点P运动的路径长是 .
答案:2π.
7.如图,⊙O的半径为8,圆心角∠AOB=120°,P为上的动点,PE⊥OA于E,PF⊥OB于F,设过P、E、O、F的圆的圆心为O ,当点F从点O开始运动时起,到点E到达点O时止,点O 运动的路径长为 .
答案:.
8.如图,正方形ABCD的边长为2,E、F分别为AD、CD上一动点,AE=DF,BE、AF交于点M,当点E从点A运动到点D时,点M运动的路径长是 .
解:易证AF⊥BE,故点M在以AB为直径的圆上运动,此时点M运动的路径长为的长,
∴的长为=.
9.如图,半径为4的⊙O中,CD为直径,弦AB⊥CD且过半径OD的中点,点E为⊙O上一动点,CF⊥AE于点F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( )
A.π B.π C.π D.π
答案:C
10.如图,半径为2cm,圆心角为90°的扇形OAB的上有一运动的点P,从点P向半径OA引垂线PH交OA于点H.设△OPH的内心为I,当点P在上从点A运动到点B时,内心I所经过的路径长为 .
答案:cm.
(三)证明与计算
11.如图,在⊙O中,=,CD⊥AB于点F,交⊙O于点D,AO的延长线交CD于点E.
(1)求证:AD=AE;
(2)若=,求的值.
解:(1)延长AE交BC于M,则AM⊥BC,BM=CM,
∴∠BAM=∠BCD=∠BAD,
又∵AB⊥CD,∴AD=AE;
(2)连接BE,设CE=5,DE=6,
易证DF=EF=3,CE=BE=5,∴BF=4,设AF=x,
在Rt△AFC中,x2+82=(x+4) 2,∴x=6,∴AB=10=AC,
∵BC===4,∴=.
12.如图,AB是⊙O的直径,点D是⊙O上一点,BC⊥CD于点C,交⊙O于点E,F是半圆的中点,EF交BD于点G,连接AE、OG.
(1)求证:点G是△ABE的内心;
(2)若BE=6,CD=4,求OG的长.
解:(1)由=可得∠AEF=∠BEF,故再证BD平分∠ABE即可;
(2)易证AE=2CD=8,AB=10,作GH⊥AB于H,GM⊥BE于M,GN⊥AE于N,
易得正方形EMGN,设GH=GM=EM=EN=x,
则BM=6-x=BH,AN=8-x=AH,
∴(6-x)+(8-x)=10,Rt△AFC中,x=2,
∴BH=4,OH=1,∴OG==.
21世纪教育网(www.21cnjy.com)
19.九年级数学(上)第24章《圆》专题卷B 核心思想方法归纳一点通(选用)
一、常见基本图形和基本结论梳理(不含相似及三角函数)
模型一 两弦垂直
1.
模型二 直径垂直于弦
2.直径AB⊥CD
3.
模型三 两半径垂直
4.CA=CD
模型四 对角互补+角平分线+内心
5.
6.
模型五 等腰图
7.
8.AB=AC基本结论
模型六 切割线图
9.基本结论
10.DE=BE=CE
模型七 双切图
11.
模型八 三切图
12. r=
(a+b+c)·r=b·h(h可求)
13.
二、综合题
(一)求最值
1.如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=2,D是线段BC上的一个动点,以AD为直径的⊙O分别交AB、AC于E、F,连接EF,则线段EF的最小值为 .
2.如图,⊙O的半径为2,弦AB的长为2,点P为优弧上一动点,AC⊥AP交直线PB于点C,则△ABC的面积的最大值是( )
A.12+6 B.6+3 C.12+3 D.6+4
3.如图,□ABCD中,∠A=60°,AD=3,CD=4,点P是边AB上的动点,将△APD沿PD折叠,点A的对应点为Q,则△BOC面积的最小值为 .
4.如图,P为⊙O内的一个定点, A为⊙O上的一个动点,射线AP、AO分别与⊙O交于B、C两点,若⊙O的半径长为3,OP=,则弦BC的最大值为( )
A.2 B.3 C. D.3
5.如图,△ABC中,AB=4,以AB为直径的⊙O分别交BC、AC于D、E,若∠DOE=60°,则CD的最大值为 .
(二)求路径长
6.如图, AB为⊙O的直径,C为半圆上一点,∠CAB=45°,AC=4,点D在⊙O上,P为CD的中点,当点D沿半圆从点B运动至点A时,点P运动的路径长是 .
7.如图,⊙O的半径为8,圆心角∠AOB=120°,P为上的动点,PE⊥OA于E,PF⊥OB于F,设过P、E、O、F的圆的圆心为O ,当点F从点O开始运动时起,到点E到达点O时止,点O 运动的路径长为 .
8.如图,正方形ABCD的边长为2,E、F分别为AD、CD上一动点,AE=DF,BE、AF交于点M,当点E从点A运动到点D时,点M运动的路径长是 .
9.如图,半径为4的⊙O中,CD为直径,弦AB⊥CD且过半径OD的中点,点E为⊙O上一动点,CF⊥AE于点F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( )
A.π B.π C.π D.π
10.如图,半径为2cm,圆心角为90°的扇形OAB的上有一运动的点P,从点P向半径OA引垂线PH交OA于点H.设△OPH的内心为I,当点P在上从点A运动到点B时,内心I所经过的路径长为 .
(三)证明与计算
11.如图,在⊙O中,=,CD⊥AB于点F,交⊙O于点D,AO的延长线交CD于点E.
(1)求证:AD=AE;
(2)若=,求的值.
12.如图,AB是⊙O的直径,点D是⊙O上一点,BC⊥CD于点C,交⊙O于点E,F是半圆的中点,EF交BD于点G,连接AE、OG.
(1)求证:点G是△ABE的内心;
(2)若BE=6,CD=4,求OG的长.
19.九年级数学(上)第24章《圆》专题卷B 核心思想方法归纳一点通(选用)
一、常见基本图形和基本结论梳理(不含相似及三角函数)
模型一 两弦垂直
1.
模型二 直径垂直于弦
2.直径AB⊥CD
3.
模型三 两半径垂直
4.CA=CD
模型四 对角互补+角平分线+内心
5.
6.
模型五 等腰图
7.
8.AB=AC基本结论
模型六 切割线图
9.基本结论
10.DE=BE=CE
模型七 双切图
11.
模型八 三切图
12. r=
(a+b+c)·r=b·h(h可求)
13.
二、综合题
(一)求最值
1.如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=2,D是线段BC上的一个动点,以AD为直径的⊙O分别交AB、AC于E、F,连接EF,则线段EF的最小值为 .
解:作直径EM,连MF,∠M=60°,EF=EM=AD.要使EF最小,只需使AD最小,故AD⊥BC,∴AD=2,EF=.
2.如图,⊙O的半径为2,弦AB的长为2,点P为优弧上一动点,AC⊥AP交直线PB于点C,则△ABC的面积的最大值是( )
A.12+6 B.6+3 C.12+3 D.6+4
提示:易求∠P=60°,∠C=30°,作△ABC的外接圆⊙O ,当AB边上的高最大,即高过⊙O 的圆心O 时,△ABC的面积最大,此时高垂直平分AB.
3.如图,□ABCD中,∠A=60°,AD=3,CD=4,点P是边AB上的动点,将△APD沿PD折叠,点A的对应点为Q,则△BOC面积的最小值为 .
解:点Q在以D为圆心,DA为半径的圆上运动,过Q作EF∥BC,分别交AB、CD于E、F,当EF与,⊙O相切时,EF与BC之间的距离最小,S△BOC最小为3-.
4.如图,P为⊙O内的一个定点, A为⊙O上的一个动点,射线AP、AO分别与⊙O交于B、C两点,若⊙O的半径长为3,OP=,则弦BC的最大值为( )
A.2 B.3 C. D.3
答案:A
5.如图,△ABC中,AB=4,以AB为直径的⊙O分别交BC、AC于D、E,若∠DOE=60°,则CD的最大值为 .
解:易证∠C=60°,连AD,则∠ADB=90°,∴CD=AC,当AC取最大值时,CD的值最大,作△ABC的外接圆⊙M,当AC为⊙M的直径时,AC最大,∴AC最大=,∴CD的最大值为.
(二)求路径长
6.如图, AB为⊙O的直径,C为半圆上一点,∠CAB=45°,AC=4,点D在⊙O上,P为CD的中点,当点D沿半圆从点B运动至点A时,点P运动的路径长是 .
答案:2π.
7.如图,⊙O的半径为8,圆心角∠AOB=120°,P为上的动点,PE⊥OA于E,PF⊥OB于F,设过P、E、O、F的圆的圆心为O ,当点F从点O开始运动时起,到点E到达点O时止,点O 运动的路径长为 .
答案:.
8.如图,正方形ABCD的边长为2,E、F分别为AD、CD上一动点,AE=DF,BE、AF交于点M,当点E从点A运动到点D时,点M运动的路径长是 .
解:易证AF⊥BE,故点M在以AB为直径的圆上运动,此时点M运动的路径长为的长,
∴的长为=.
9.如图,半径为4的⊙O中,CD为直径,弦AB⊥CD且过半径OD的中点,点E为⊙O上一动点,CF⊥AE于点F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( )
A.π B.π C.π D.π
答案:C
10.如图,半径为2cm,圆心角为90°的扇形OAB的上有一运动的点P,从点P向半径OA引垂线PH交OA于点H.设△OPH的内心为I,当点P在上从点A运动到点B时,内心I所经过的路径长为 .
答案:cm.
(三)证明与计算
11.如图,在⊙O中,=,CD⊥AB于点F,交⊙O于点D,AO的延长线交CD于点E.
(1)求证:AD=AE;
(2)若=,求的值.
解:(1)延长AE交BC于M,则AM⊥BC,BM=CM,
∴∠BAM=∠BCD=∠BAD,
又∵AB⊥CD,∴AD=AE;
(2)连接BE,设CE=5,DE=6,
易证DF=EF=3,CE=BE=5,∴BF=4,设AF=x,
在Rt△AFC中,x2+82=(x+4) 2,∴x=6,∴AB=10=AC,
∵BC===4,∴=.
12.如图,AB是⊙O的直径,点D是⊙O上一点,BC⊥CD于点C,交⊙O于点E,F是半圆的中点,EF交BD于点G,连接AE、OG.
(1)求证:点G是△ABE的内心;
(2)若BE=6,CD=4,求OG的长.
解:(1)由=可得∠AEF=∠BEF,故再证BD平分∠ABE即可;
(2)易证AE=2CD=8,AB=10,作GH⊥AB于H,GM⊥BE于M,GN⊥AE于N,
易得正方形EMGN,设GH=GM=EM=EN=x,
则BM=6-x=BH,AN=8-x=AH,
∴(6-x)+(8-x)=10,Rt△AFC中,x=2,
∴BH=4,OH=1,∴OG==.
21世纪教育网(www.21cnjy.com)
同课章节目录
