九年级数学(上)第24章《圆》单元检测题(含答案)
文档属性
| 名称 | 九年级数学(上)第24章《圆》单元检测题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 311.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-18 19:20:18 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
20九年级数学(上)第24章《圆》单元检测题
(考试范围:全章综合测试 解答参考时间:120分钟 满分120分)
一、选择题(每小题3分,共30分)
1.若⊙O的半径为8cm,点A到圆心O的距离为10cm,那么点A与⊙O的位置关系是( )
A.点A在⊙O内 B.点A在⊙O上 C.点A在⊙O外 D.不能确定
2.已知⊙O的半径为5,圆心到直线l的距离为6,则直线l与⊙O的位置关系是( )
A.相交 B.相离 C.相切 D.相交或相切
3.如图,在⊙O中,圆心角∠BOC=80°,则圆周角∠BAC等于( )
A.60° B.50° C.40° D.30°
4.如图,AB为⊙O的直径,∠BED=35°,则∠ACD的度数是( )
A.55° B.50° C.45° D.30°
5.在Rt△ABC中,两直角边AC=6cm,BC=8cm,则它的外接圆的面积为( )
A.15πcm2 B.25πcm2 C.50πcm2 D.100πcm2
6.已知圆锥的底面半径是4,母线长是5,则该圆锥的侧面积是( )
A.10π B.15π C.25π D.20π
7.如图,在边长为1的正方形组成的网格中,△ABC的顶点都在格点上,将△ABC绕点C顺时针旋转60°,则顶点A所经过的路径长为( )
A.10π B.π C. D.π
8.半径为R的圆内接正三角形的面积是( )
A.R2 B.πR2 C.R2 D.R2
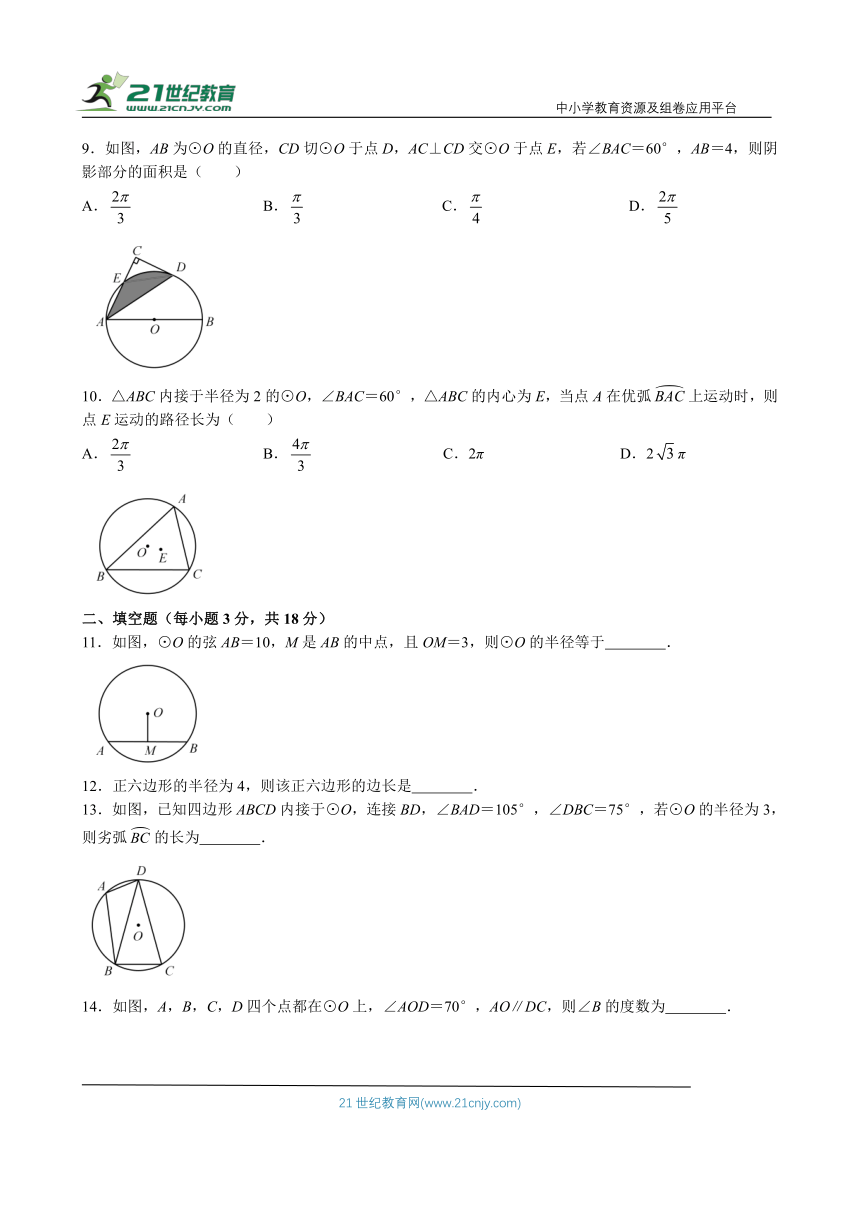
9.如图,AB为⊙O的直径,CD切⊙O于点D,AC⊥CD交⊙O于点E,若∠BAC=60°,AB=4,则阴影部分的面积是( )
A. B. C. D.
10.△ABC内接于半径为2的⊙O,∠BAC=60°,△ABC的内心为E,当点A在优弧上运动时,则点E运动的路径长为( )
A. B. C.2π D.2π
二、填空题(每小题3分,共18分)
11.如图,⊙O的弦AB=10,M是AB的中点,且OM=3,则⊙O的半径等于 .
12.正六边形的半径为4,则该正六边形的边长是 .
13.如图,已知四边形ABCD内接于⊙O,连接BD,∠BAD=105°,∠DBC=75°,若⊙O的半径为3,则劣弧的长为 .
14.如图,A,B,C,D四个点都在⊙O上,∠AOD=70°,AO∥DC,则∠B的度数为 .
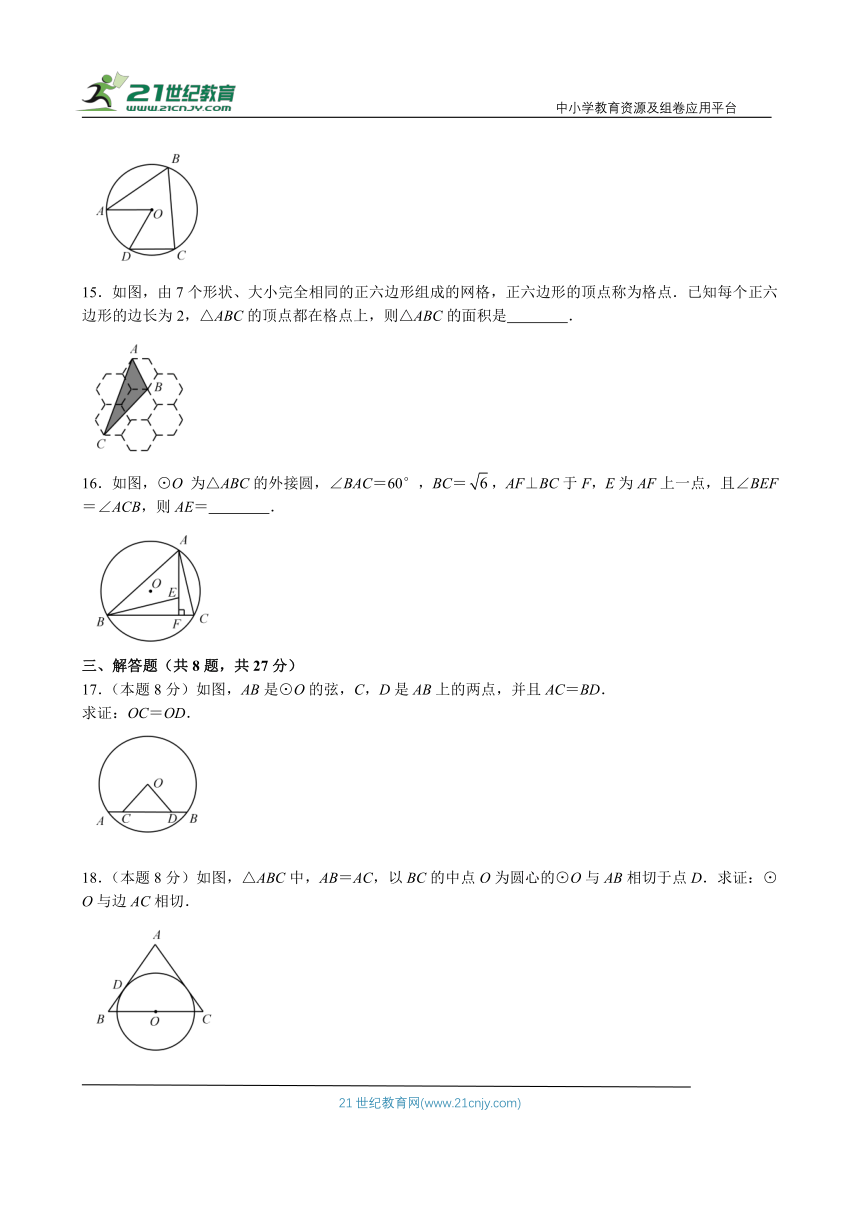
15.如图,由7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点.已知每个正六边形的边长为2,△ABC的顶点都在格点上,则△ABC的面积是 .
16.如图,⊙O 为△ABC的外接圆,∠BAC=60°,BC=,AF⊥BC于F,E为AF上一点,且∠BEF=∠ACB,则AE= .
三、解答题(共8题,共27分)
17.(本题8分)如图,AB是⊙O的弦,C,D是AB上的两点,并且AC=BD.
求证:OC=OD.
18.(本题8分)如图,△ABC中,AB=AC,以BC的中点O为圆心的⊙O与AB相切于点D.求证:⊙O与边AC相切.
19.(本题8分)如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.
(1)求证:MD=ME;
(2)连接OD,OE,当∠A的度数为 时,四边形ODME是菱形.
20.(本题8分)如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
(1)把△ABC沿BA方向平移后,点A移动到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在网格中画出旋转后的△A2B2C2;
(3)如果网格中小正方形的边长为1,直接写出点B经过(1)、(2)变换的路径总长.
21.(本题8分)如图,平面直角坐标系中,⊙P与x轴分别交于A,B两点,点P的坐标为(6,-2),AB=4.
(1)求⊙P的半径长;
(2)将⊙P沿y轴上下平移,直接写出⊙P与x轴相切时平移的距离.
22.(本题10分)如图,在⊙O中,=,BD⊥AC于E,交⊙O于点D,延长AO交BD于点F,连接CD.
(1)求证:BD-CD=DF;
(2)若BD=11,CD=5,求AB的长.
23.(本题10分)如图,在Rt△ABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A,B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.
(1)求证:AE=BF;
(2)连接GB,EF,求证:GB∥EF.
24.(本题12分)如图,已知A,B两点的坐标分别为A(2,0),B(0,2),点P是过A,O,B的圆上的一点,且=.
(1)如图1,若=,求PM的长;
(2)如图2,点Q是上一点,且=+,求PQ的长;
(3)如图3,连接BP,AP,在射线PB上任取一点E,连AE,将线段AE绕A点顺时针旋转90°到AF,连接BF,交射线AP于点G,当E在射线PB上运动时(不与B,P重合),求的值.
20九年级数学(上)第24章《圆》单元检测题
(考试范围:全章综合测试 解答参考时间:120分钟 满分120分)
一、选择题(每小题3分,共30分)
1.若⊙O的半径为8cm,点A到圆心O的距离为10cm,那么点A与⊙O的位置关系是( )
A.点A在⊙O内 B.点A在⊙O上 C.点A在⊙O外 D.不能确定
答案:C
2.已知⊙O的半径为5,圆心到直线l的距离为6,则直线l与⊙O的位置关系是( )
A.相交 B.相离 C.相切 D.相交或相切
答案:B
3.如图,在⊙O中,圆心角∠BOC=80°,则圆周角∠BAC等于( )
A.60° B.50° C.40° D.30°
答案:C
4.如图,AB为⊙O的直径,∠BED=35°,则∠ACD的度数是( )
A.55° B.50° C.45° D.30°
答案:A
5.在Rt△ABC中,两直角边AC=6cm,BC=8cm,则它的外接圆的面积为( )
A.15πcm2 B.25πcm2 C.50πcm2 D.100πcm2
答案:B
6.已知圆锥的底面半径是4,母线长是5,则该圆锥的侧面积是( )
A.10π B.15π C.25π D.20π
答案:D
7.如图,在边长为1的正方形组成的网格中,△ABC的顶点都在格点上,将△ABC绕点C顺时针旋转60°,则顶点A所经过的路径长为( )
A.10π B.π C. D.π
答案:B
8.半径为R的圆内接正三角形的面积是( )
A.R2 B.πR2 C.R2 D.R2
答案:C
9.如图,AB为⊙O的直径,CD切⊙O于点D,AC⊥CD交⊙O于点E,若∠BAC=60°,AB=4,则阴影部分的面积是( )
A. B. C. D.
答案:A
10.△ABC内接于半径为2的⊙O,∠BAC=60°,△ABC的内心为E,当点A在优弧上运动时,则点E运动的路径长为( )
A. B. C.2π D.2π
解:连AE并延长交⊙O于点D,连DB,DC,DO,BO,BE,∵∠BAC=60°,△ABC的内心为E,∴易证DB=DE=DC=OD,∴点E运动的路径是以D为圆心,OD为半径的优弧,∵∠BDC=180°-∠BAC=120°,OD=2,∴的长l==.
二、填空题(每小题3分,共18分)
11.如图,⊙O的弦AB=10,M是AB的中点,且OM=3,则⊙O的半径等于 .
答案:
12.正六边形的半径为4,则该正六边形的边长是 .
答案:4
13.如图,已知四边形ABCD内接于⊙O,连接BD,∠BAD=105°,∠DBC=75°,若⊙O的半径为3,则劣弧的长为 .
答案:π
14.如图,A,B,C,D四个点都在⊙O上,∠AOD=70°,AO∥DC,则∠B的度数为 .
答案:55°
15.如图,由7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点.已知每个正六边形的边长为2,△ABC的顶点都在格点上,则△ABC的面积是 .
答案: 8
16.如图,⊙O 为△ABC的外接圆,∠BAC=60°,BC=,AF⊥BC于F,E为AF上一点,且∠BEF=∠ACB,则AE= .
解:作直径CM,连接BM,则BM=BC=,连接AM,∵CM为直径,∴∠MBC=90°=∠MAC,∴∠ACB=∠MAF=∠BEF,∴AM∥BE,又BM∥AF,∴四边形AMBE为平行四边形,∴AE=BM=.
三、解答题(共8题,共27分)
17.(本题8分)如图,AB是⊙O的弦,C,D是AB上的两点,并且AC=BD.
求证:OC=OD.
解:过O作OM⊥AB于M,利用垂径定理.
18.(本题8分)如图,△ABC中,AB=AC,以BC的中点O为圆心的⊙O与AB相切于点D.
求证:⊙O与边AC相切.
证:连接OD,OA,作OE⊥AC于E.∵AB=AC,OB=OC,∴OA平分∠BAC,又∵OD⊥AB,∴OE=OD,∴⊙O与边AC相切.
19.(本题8分)如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.
(1)求证:MD=ME;
(2)连接OD,OE,当∠A的度数为 时,四边形ODME是菱形.
解:(1)证MA=MB,∠A=∠ABM,连DE,∵∠MDE=∠ABM,∠MED=∠A,∴∠MDE=∠MED,∴MD=ME;
(2)60°.
20.(本题8分)如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
(1)把△ABC沿BA方向平移后,点A移动到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在网格中画出旋转后的△A2B2C2;
(3)如果网格中小正方形的边长为1,直接写出点B经过(1)、(2)变换的路径总长.
解:(1)略;
(2)略;
(3)2+.
21.(本题8分)如图,平面直角坐标系中,⊙P与x轴分别交于A,B两点,点P的坐标为(6,-2),AB=4.
(1)求⊙P的半径长;
(2)将⊙P沿y轴上下平移,直接写出⊙P与x轴相切时平移的距离.
解:(1)4;
(2)2或6.
22.(本题10分)如图,在⊙O中,=,BD⊥AC于E,交⊙O于点D,延长AO交BD于点F,连接CD.
(1)求证:BD-CD=DF;
(2)若BD=11,CD=5,求AB的长.
解:(1)易证AF垂直平分BC,∴BF=CF,易证∠ACD=∠ABF=∠ACF,又∵CE⊥DF,∴CD=CF,∴CD=BF,∴BD-CD=BD-BF=DF;
(2)由(1)知CD=BF=CF=5,∴DF=6,∵CD=CF,CE⊥DF,∴DE=EF=3,∴CE=,=4,设AB=x,在△ABE中有:x2=(x-4)2+(8)2,∴x=10,∴AB=10.
23.(本题10分)如图,在Rt△ABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A,B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.
(1)求证:AE=BF;
(2)连接GB,EF,求证:GB∥EF.
解:(1)连接BD,在Rt△ABC中,∠ABC=90°,AB=BC,∴∠A=∠C=45°,∵AB为⊙O的直径,∴∠ADB=90°,即BD⊥AC,∴AD=DC=BD=AC,∴∠CBD=∠C=45°,∴∠A=∠FBD,∵DF⊥DG,∴∠FDG=90°,∴∠FDB+∠BDG=90°,∵∠EDA+∠BDG=90°,∴∠EDA=∠FDB,∴△AED≌△BFD(ASA),∴AE=BF;
(2)∵由△AED≌△BFD,∴DE=DF,∵∠EDF=90°,∴△EDF是等腰直角三角形,∴∠DEF=45°,∵∠G=∠A=45°,∴∠G=∠DEF,∴GB∥EF;
(3)易知AE=BF=2,DE=DF=,设⊙O的半径为R,连OD,则OD⊥AB,OE=R-2,在Rt△OED中,(R-2)2+R2=()2,R2-2R-3=0, R=3,∴AB=6,∴AC=AB=6.
24.(本题12分)如图,已知A,B两点的坐标分别为A(2,0),B(0,2),点P是过A,O,B的圆上的一点,且=.
(1)如图1,若=,求PM的长;
(2)如图2,点Q是上一点,且=+,求PQ的长;
(3)如图3,连接BP,AP,在射线PB上任取一点E,连AE,将线段AE绕A点顺时针旋转90°到AF,连接BF,交射线AP于点G,当E在射线PB上运动时(不与B,P重合),求的值.
解:(1)易求∠OBA=60°,∠OAB=30°,∠ABM=∠OBM=∠AOM=30°,∴∠BOM=120°,∴∠BPM=60°,易求∠BMP=∠BAP=45°,作BC⊥PM于C,∵AB==4,∴PB=AB=2,∴BC=PC==MC,∴PC=+;
(2)连接QA,PB,PA,则∠BPA=90°,PA=PB,易证=,AOBQ为矩形,∠PQB=45°,在BQ上截取BM=AQ,证△BMP≌△AQP,△MPQ是等腰直角三角形,∴BQ-AQ=PQ,∴2-2=PQ,∴PQ=-.
(3)过F作FH⊥PA于H,证△FAH≌△AEP,△BPG≌△FHG,∴AH=PE,∵PA=PB,∴BE=PH=2PG,∴=2.
21世纪教育网(www.21cnjy.com)
20九年级数学(上)第24章《圆》单元检测题
(考试范围:全章综合测试 解答参考时间:120分钟 满分120分)
一、选择题(每小题3分,共30分)
1.若⊙O的半径为8cm,点A到圆心O的距离为10cm,那么点A与⊙O的位置关系是( )
A.点A在⊙O内 B.点A在⊙O上 C.点A在⊙O外 D.不能确定
2.已知⊙O的半径为5,圆心到直线l的距离为6,则直线l与⊙O的位置关系是( )
A.相交 B.相离 C.相切 D.相交或相切
3.如图,在⊙O中,圆心角∠BOC=80°,则圆周角∠BAC等于( )
A.60° B.50° C.40° D.30°
4.如图,AB为⊙O的直径,∠BED=35°,则∠ACD的度数是( )
A.55° B.50° C.45° D.30°
5.在Rt△ABC中,两直角边AC=6cm,BC=8cm,则它的外接圆的面积为( )
A.15πcm2 B.25πcm2 C.50πcm2 D.100πcm2
6.已知圆锥的底面半径是4,母线长是5,则该圆锥的侧面积是( )
A.10π B.15π C.25π D.20π
7.如图,在边长为1的正方形组成的网格中,△ABC的顶点都在格点上,将△ABC绕点C顺时针旋转60°,则顶点A所经过的路径长为( )
A.10π B.π C. D.π
8.半径为R的圆内接正三角形的面积是( )
A.R2 B.πR2 C.R2 D.R2
9.如图,AB为⊙O的直径,CD切⊙O于点D,AC⊥CD交⊙O于点E,若∠BAC=60°,AB=4,则阴影部分的面积是( )
A. B. C. D.
10.△ABC内接于半径为2的⊙O,∠BAC=60°,△ABC的内心为E,当点A在优弧上运动时,则点E运动的路径长为( )
A. B. C.2π D.2π
二、填空题(每小题3分,共18分)
11.如图,⊙O的弦AB=10,M是AB的中点,且OM=3,则⊙O的半径等于 .
12.正六边形的半径为4,则该正六边形的边长是 .
13.如图,已知四边形ABCD内接于⊙O,连接BD,∠BAD=105°,∠DBC=75°,若⊙O的半径为3,则劣弧的长为 .
14.如图,A,B,C,D四个点都在⊙O上,∠AOD=70°,AO∥DC,则∠B的度数为 .
15.如图,由7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点.已知每个正六边形的边长为2,△ABC的顶点都在格点上,则△ABC的面积是 .
16.如图,⊙O 为△ABC的外接圆,∠BAC=60°,BC=,AF⊥BC于F,E为AF上一点,且∠BEF=∠ACB,则AE= .
三、解答题(共8题,共27分)
17.(本题8分)如图,AB是⊙O的弦,C,D是AB上的两点,并且AC=BD.
求证:OC=OD.
18.(本题8分)如图,△ABC中,AB=AC,以BC的中点O为圆心的⊙O与AB相切于点D.求证:⊙O与边AC相切.
19.(本题8分)如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.
(1)求证:MD=ME;
(2)连接OD,OE,当∠A的度数为 时,四边形ODME是菱形.
20.(本题8分)如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
(1)把△ABC沿BA方向平移后,点A移动到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在网格中画出旋转后的△A2B2C2;
(3)如果网格中小正方形的边长为1,直接写出点B经过(1)、(2)变换的路径总长.
21.(本题8分)如图,平面直角坐标系中,⊙P与x轴分别交于A,B两点,点P的坐标为(6,-2),AB=4.
(1)求⊙P的半径长;
(2)将⊙P沿y轴上下平移,直接写出⊙P与x轴相切时平移的距离.
22.(本题10分)如图,在⊙O中,=,BD⊥AC于E,交⊙O于点D,延长AO交BD于点F,连接CD.
(1)求证:BD-CD=DF;
(2)若BD=11,CD=5,求AB的长.
23.(本题10分)如图,在Rt△ABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A,B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.
(1)求证:AE=BF;
(2)连接GB,EF,求证:GB∥EF.
24.(本题12分)如图,已知A,B两点的坐标分别为A(2,0),B(0,2),点P是过A,O,B的圆上的一点,且=.
(1)如图1,若=,求PM的长;
(2)如图2,点Q是上一点,且=+,求PQ的长;
(3)如图3,连接BP,AP,在射线PB上任取一点E,连AE,将线段AE绕A点顺时针旋转90°到AF,连接BF,交射线AP于点G,当E在射线PB上运动时(不与B,P重合),求的值.
20九年级数学(上)第24章《圆》单元检测题
(考试范围:全章综合测试 解答参考时间:120分钟 满分120分)
一、选择题(每小题3分,共30分)
1.若⊙O的半径为8cm,点A到圆心O的距离为10cm,那么点A与⊙O的位置关系是( )
A.点A在⊙O内 B.点A在⊙O上 C.点A在⊙O外 D.不能确定
答案:C
2.已知⊙O的半径为5,圆心到直线l的距离为6,则直线l与⊙O的位置关系是( )
A.相交 B.相离 C.相切 D.相交或相切
答案:B
3.如图,在⊙O中,圆心角∠BOC=80°,则圆周角∠BAC等于( )
A.60° B.50° C.40° D.30°
答案:C
4.如图,AB为⊙O的直径,∠BED=35°,则∠ACD的度数是( )
A.55° B.50° C.45° D.30°
答案:A
5.在Rt△ABC中,两直角边AC=6cm,BC=8cm,则它的外接圆的面积为( )
A.15πcm2 B.25πcm2 C.50πcm2 D.100πcm2
答案:B
6.已知圆锥的底面半径是4,母线长是5,则该圆锥的侧面积是( )
A.10π B.15π C.25π D.20π
答案:D
7.如图,在边长为1的正方形组成的网格中,△ABC的顶点都在格点上,将△ABC绕点C顺时针旋转60°,则顶点A所经过的路径长为( )
A.10π B.π C. D.π
答案:B
8.半径为R的圆内接正三角形的面积是( )
A.R2 B.πR2 C.R2 D.R2
答案:C
9.如图,AB为⊙O的直径,CD切⊙O于点D,AC⊥CD交⊙O于点E,若∠BAC=60°,AB=4,则阴影部分的面积是( )
A. B. C. D.
答案:A
10.△ABC内接于半径为2的⊙O,∠BAC=60°,△ABC的内心为E,当点A在优弧上运动时,则点E运动的路径长为( )
A. B. C.2π D.2π
解:连AE并延长交⊙O于点D,连DB,DC,DO,BO,BE,∵∠BAC=60°,△ABC的内心为E,∴易证DB=DE=DC=OD,∴点E运动的路径是以D为圆心,OD为半径的优弧,∵∠BDC=180°-∠BAC=120°,OD=2,∴的长l==.
二、填空题(每小题3分,共18分)
11.如图,⊙O的弦AB=10,M是AB的中点,且OM=3,则⊙O的半径等于 .
答案:
12.正六边形的半径为4,则该正六边形的边长是 .
答案:4
13.如图,已知四边形ABCD内接于⊙O,连接BD,∠BAD=105°,∠DBC=75°,若⊙O的半径为3,则劣弧的长为 .
答案:π
14.如图,A,B,C,D四个点都在⊙O上,∠AOD=70°,AO∥DC,则∠B的度数为 .
答案:55°
15.如图,由7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点.已知每个正六边形的边长为2,△ABC的顶点都在格点上,则△ABC的面积是 .
答案: 8
16.如图,⊙O 为△ABC的外接圆,∠BAC=60°,BC=,AF⊥BC于F,E为AF上一点,且∠BEF=∠ACB,则AE= .
解:作直径CM,连接BM,则BM=BC=,连接AM,∵CM为直径,∴∠MBC=90°=∠MAC,∴∠ACB=∠MAF=∠BEF,∴AM∥BE,又BM∥AF,∴四边形AMBE为平行四边形,∴AE=BM=.
三、解答题(共8题,共27分)
17.(本题8分)如图,AB是⊙O的弦,C,D是AB上的两点,并且AC=BD.
求证:OC=OD.
解:过O作OM⊥AB于M,利用垂径定理.
18.(本题8分)如图,△ABC中,AB=AC,以BC的中点O为圆心的⊙O与AB相切于点D.
求证:⊙O与边AC相切.
证:连接OD,OA,作OE⊥AC于E.∵AB=AC,OB=OC,∴OA平分∠BAC,又∵OD⊥AB,∴OE=OD,∴⊙O与边AC相切.
19.(本题8分)如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.
(1)求证:MD=ME;
(2)连接OD,OE,当∠A的度数为 时,四边形ODME是菱形.
解:(1)证MA=MB,∠A=∠ABM,连DE,∵∠MDE=∠ABM,∠MED=∠A,∴∠MDE=∠MED,∴MD=ME;
(2)60°.
20.(本题8分)如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
(1)把△ABC沿BA方向平移后,点A移动到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在网格中画出旋转后的△A2B2C2;
(3)如果网格中小正方形的边长为1,直接写出点B经过(1)、(2)变换的路径总长.
解:(1)略;
(2)略;
(3)2+.
21.(本题8分)如图,平面直角坐标系中,⊙P与x轴分别交于A,B两点,点P的坐标为(6,-2),AB=4.
(1)求⊙P的半径长;
(2)将⊙P沿y轴上下平移,直接写出⊙P与x轴相切时平移的距离.
解:(1)4;
(2)2或6.
22.(本题10分)如图,在⊙O中,=,BD⊥AC于E,交⊙O于点D,延长AO交BD于点F,连接CD.
(1)求证:BD-CD=DF;
(2)若BD=11,CD=5,求AB的长.
解:(1)易证AF垂直平分BC,∴BF=CF,易证∠ACD=∠ABF=∠ACF,又∵CE⊥DF,∴CD=CF,∴CD=BF,∴BD-CD=BD-BF=DF;
(2)由(1)知CD=BF=CF=5,∴DF=6,∵CD=CF,CE⊥DF,∴DE=EF=3,∴CE=,=4,设AB=x,在△ABE中有:x2=(x-4)2+(8)2,∴x=10,∴AB=10.
23.(本题10分)如图,在Rt△ABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A,B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.
(1)求证:AE=BF;
(2)连接GB,EF,求证:GB∥EF.
解:(1)连接BD,在Rt△ABC中,∠ABC=90°,AB=BC,∴∠A=∠C=45°,∵AB为⊙O的直径,∴∠ADB=90°,即BD⊥AC,∴AD=DC=BD=AC,∴∠CBD=∠C=45°,∴∠A=∠FBD,∵DF⊥DG,∴∠FDG=90°,∴∠FDB+∠BDG=90°,∵∠EDA+∠BDG=90°,∴∠EDA=∠FDB,∴△AED≌△BFD(ASA),∴AE=BF;
(2)∵由△AED≌△BFD,∴DE=DF,∵∠EDF=90°,∴△EDF是等腰直角三角形,∴∠DEF=45°,∵∠G=∠A=45°,∴∠G=∠DEF,∴GB∥EF;
(3)易知AE=BF=2,DE=DF=,设⊙O的半径为R,连OD,则OD⊥AB,OE=R-2,在Rt△OED中,(R-2)2+R2=()2,R2-2R-3=0, R=3,∴AB=6,∴AC=AB=6.
24.(本题12分)如图,已知A,B两点的坐标分别为A(2,0),B(0,2),点P是过A,O,B的圆上的一点,且=.
(1)如图1,若=,求PM的长;
(2)如图2,点Q是上一点,且=+,求PQ的长;
(3)如图3,连接BP,AP,在射线PB上任取一点E,连AE,将线段AE绕A点顺时针旋转90°到AF,连接BF,交射线AP于点G,当E在射线PB上运动时(不与B,P重合),求的值.
解:(1)易求∠OBA=60°,∠OAB=30°,∠ABM=∠OBM=∠AOM=30°,∴∠BOM=120°,∴∠BPM=60°,易求∠BMP=∠BAP=45°,作BC⊥PM于C,∵AB==4,∴PB=AB=2,∴BC=PC==MC,∴PC=+;
(2)连接QA,PB,PA,则∠BPA=90°,PA=PB,易证=,AOBQ为矩形,∠PQB=45°,在BQ上截取BM=AQ,证△BMP≌△AQP,△MPQ是等腰直角三角形,∴BQ-AQ=PQ,∴2-2=PQ,∴PQ=-.
(3)过F作FH⊥PA于H,证△FAH≌△AEP,△BPG≌△FHG,∴AH=PE,∵PA=PB,∴BE=PH=2PG,∴=2.
21世纪教育网(www.21cnjy.com)
同课章节目录
