九年级数学(上)第25章《概率初步》单元检测题(含答案)
文档属性
| 名称 | 九年级数学(上)第25章《概率初步》单元检测题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 321.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-18 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
23.九年级数学(上)第25章《概率初步》单元检测题
(测试范围:全章综合侧试 解答参考时间:90分钟 满分120分)
一、选择题(每小题3分,共30分)
1.“抛一枚均匀硬币,落地后正面朝上”这一事件是( )
A.必然事件 B.随机事件 C.确定事件 D.不可能事件
2.从只装有4个红球的袋中随机摸出一球,若摸到白球的概率是P1,摸到红球的概率是P2,则( )
A. P1=1,P2=1 B. P1=0,P2=1 C. P1=0,P2= D. P1=P2=
3.如图,一个可以启由转动的转盘被等分成6个扇形区域,并涂上了相应的颜色,转动转盘,转盘停止后,指针指向蓝色区域的概率是( )
A. B. C. D.
4.掷一个质地均匀的正方体般子,当般子停止后,朝上一面的点数为5的概率是( )
A.1 B. C. D.0
5.在抛掷一枚硬币的实验中,某一组做了500次试验,其出现正面的频率是49. 6%,可以推知出现正面的次数是( )
A.248 B.250 C.258 D.无法确定
6.在一个不透明的袋子中装有除颜色外其它均相同的3个红球和2个白球,从中任意摸出一个球,则摸出白球的概率是( )
A. B. C. D.
7.一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有6个黄球.每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色 后再放回盒子,通过大量重复摸球实验后发现,摸到黄球的频率稳定在30%,那么可以推算出n大约是( )
A.6 B. 10 C. 18 D. 20
8.经过某十字路口的汽车,可能直行,也可能左转或者右转.如果这三种可能性大小相同,则经过这个十字路口的两辆汽车都直行的概率是( )
A. B. C. D.
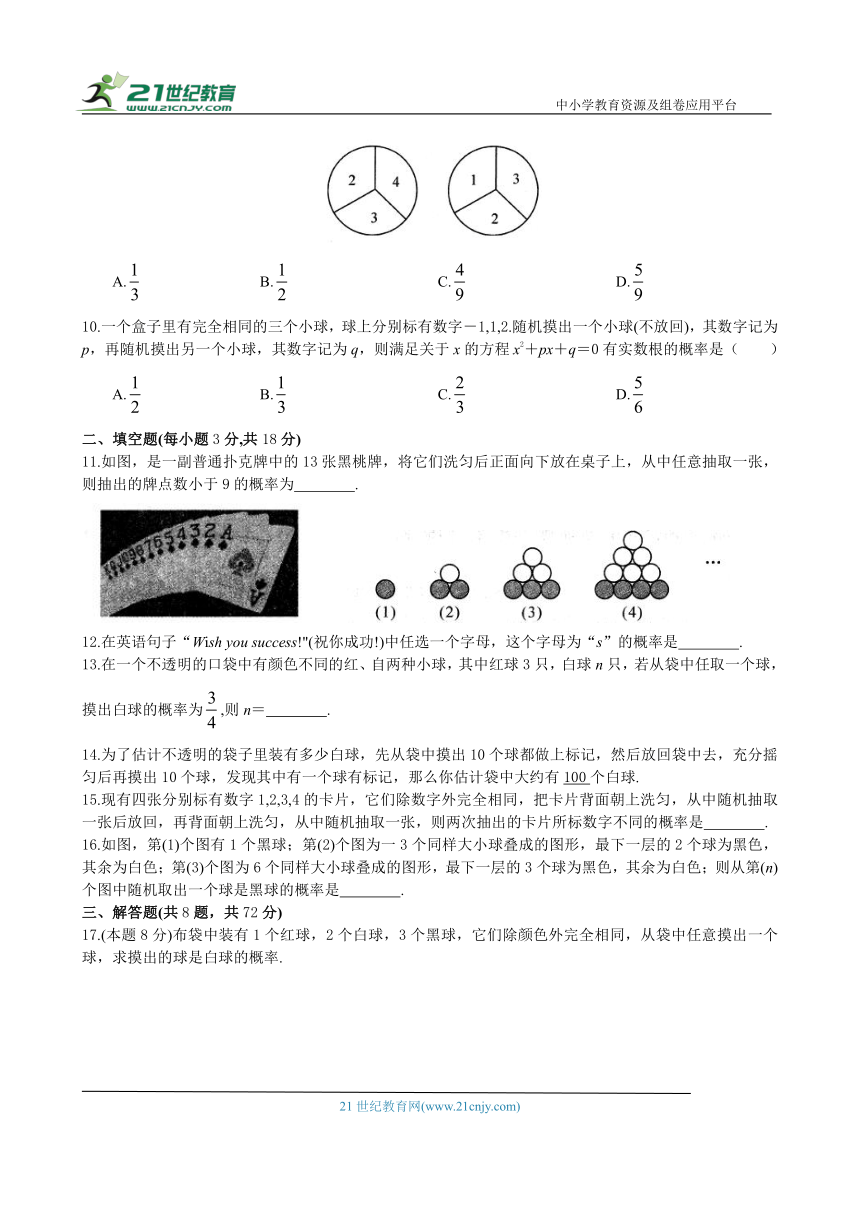
9.如图,转动两个转盘,当指针所指的数之和为奇数时,小明胜,否则小亮胜,则小明获胜的概率是( )
A. B. C. D.
10.一个盒子里有完全相同的三个小球,球上分别标有数字-1,1,2.随机摸出一个小球(不放回),其数字记为p,再随机摸出另一个小球,其数字记为q,则满足关于x的方程x2+px+q=0有实数根的概率是( )
A. B. C. D.
二、填空题(每小题3分,共18分)
11.如图,是一副普通扑克牌中的13张黑桃牌,将它们洗匀后正面向下放在桌子上,从中任意抽取一张,则抽出的牌点数小于9的概率为 .
12.在英语句子“Wish you success!"(祝你成功!)中任选一个字母,这个字母为“s”的概率是 .
13.在一个不透明的口袋中有颜色不同的红、自两种小球,其中红球3只,白球n只,若从袋中任取一个球,摸出白球的概率为,则n= .
14.为了估计不透明的袋子里装有多少白球,先从袋中摸出10个球都做上标记,然后放回袋中去,充分摇匀后再摸出10个球,发现其中有一个球有标记,那么你估计袋中大约有100个白球.
15.现有四张分别标有数字1,2,3,4的卡片,它们除数字外完全相同,把卡片背面朝上洗匀,从中随机抽取一张后放回,再背面朝上洗匀,从中随机抽取一张,则两次抽出的卡片所标数字不同的概率是 .
16.如图,第(1)个图有1个黑球;第(2)个图为一3个同样大小球叠成的图形,最下一层的2个球为黑色,其余为白色;第(3)个图为6个同样大小球叠成的图形,最下一层的3个球为黑色,其余为白色;则从第(n)个图中随机取出一个球是黑球的概率是 .
三、解答题(共8题,共72分)
17.(本题8分)布袋中装有1个红球,2个白球,3个黑球,它们除颜色外完全相同,从袋中任意摸出一个球,求摸出的球是白球的概率.
18.(本题8分)一个口袋中有3个大小相同的小球,球面上分别写有数字1,2,3,从袋中随机地摸出一个小球,记录下数字后放回,再随机地摸出一个小球.
(1)请用树形图或列表法中的一种,列举出两次摸出的球上数字的所有可能结果;
(2)求两次摸出的球上的数字和为偶数的概率.
19.(本题8分)商店只有雪碧、可乐、果汁、奶汁四种饮料,每种饮料数量充足,某同学去该店购买饮料,每种饮料被选中的可能性相同.
(1)若他去买一瓶饮料,则他买到奶汁的概率是 ;
(2)若他两次去买饮料,每次买一瓶,且两次所买饮料品种不同,请用树状图或列表法求出他恰好买到雪碧和奶汁的概率.
20.(本题8分)在一个不透明的口袋中装有红、白、黑三种颜色的小球若干个,它们只有颜色不同,其中有白球2个、黑球1个。己知从中任意摸出1个球得白球的概率为.
(1)求口袋中有多少个红球;
(2)求从袋中一次摸出2个球,得一红一白的概率.(要求画出树状图)
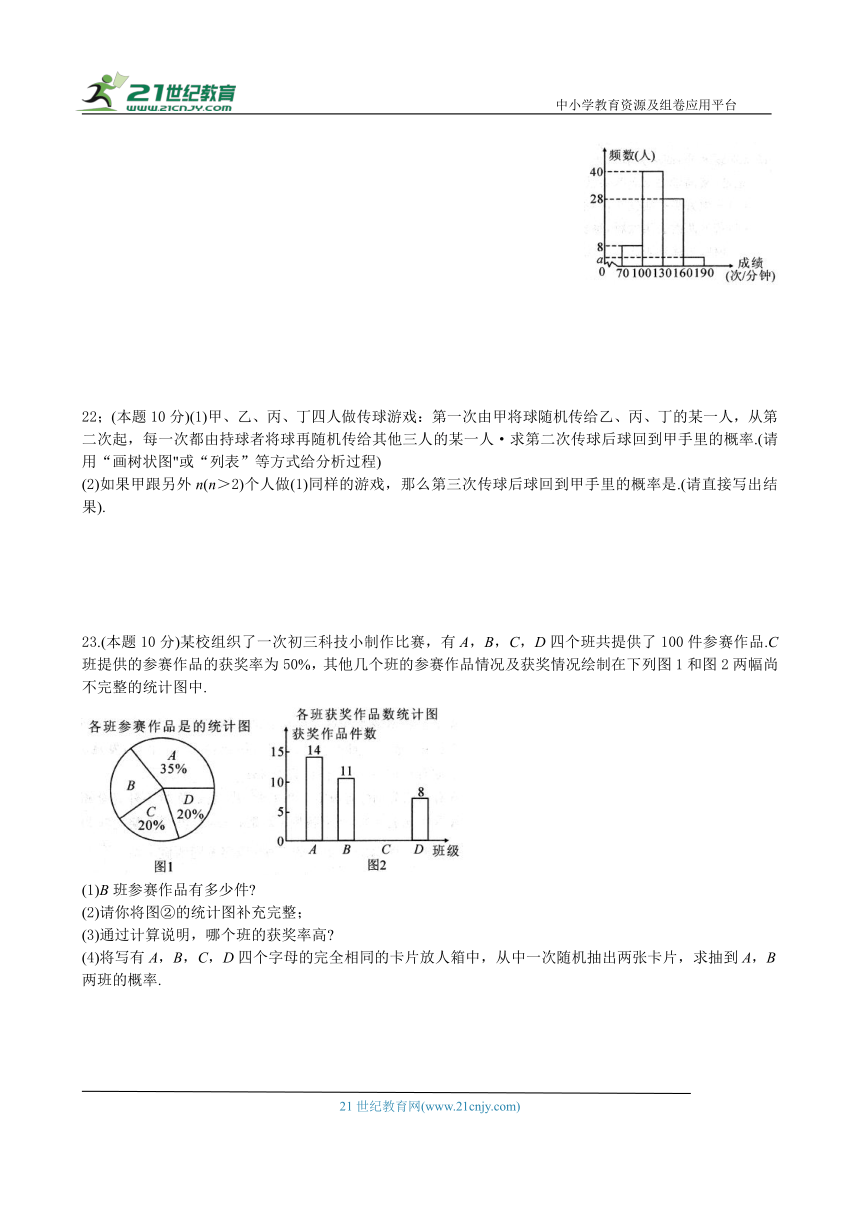
21.(本题8分)“阳光体育”运动关乎每个学生未来的幸福生活,今年五月,我市某校开展了以“阳光体育我是冠军”为主题的一分钟限时跳绳比赛,要求每个班选2-3名选手参赛,现将80名选手比赛成绩(单位:次/分钟)进行统计.绘制成频数分布直方图,如图所示.
(1)图中a值为 ;
(2)将跳绳次数在160—190的选手依次记为A1,A2,…An,从中随机抽取两名选手作经一验交流,请用画树状图或列表法求恰好抽取到的选手是A1和A2的概率.
22;(本题10分)(1)甲、乙、丙、丁四人做传球游戏:第一次由甲将球随机传给乙、丙、丁的某一人,从第二次起,每一次都由持球者将球再随机传给其他三人的某一人·求第二次传球后球回到甲手里的概率.(请用“画树状图"或“列表”等方式给分析过程)
(2)如果甲跟另外n(n>2)个人做(1)同样的游戏,那么第三次传球后球回到甲手里的概率是.(请直接写出结果).
23.(本题10分)某校组织了一次初三科技小制作比赛,有A,B,C,D四个班共提供了100件参赛作品.C班提供的参赛作品的获奖率为50%,其他几个班的参赛作品情况及获奖情况绘制在下列图1和图2两幅尚不完整的统计图中.
(1)B班参赛作品有多少件
(2)请你将图②的统计图补充完整;
(3)通过计算说明,哪个班的获奖率高
(4)将写有A,B,C,D四个字母的完全相同的卡片放人箱中,从中一次随机抽出两张卡片,求抽到A,B两班的概率.
24.(本题12分)已知M(x,y)是平面直角坐标系xOy中的点,其中x是从1,2,3三个数中任取的一个数,y是从1,2,3,4四个数中任取的一个数.
(1)计算由x;y确定的点M(x,y)在函数y=-x+5的图象上的概率;
(2)小明和小红约定做一个游戏,其规则为:若x,y满足xy>6则小明胜,若x,y满足xy<6则小红胜,这个游戏公平吗 说明理由.若不公平,请写出公平的游戏规则;
(3)定义“点M(x,y)在直线x+ y=n上”为事件A(2≤n≤7, n为整数),则当A的概率最大时,n的所有可能的值为 .(不需要解答过程)
23.九年级数学(上)第25章《概率初步》单元检测题
(测试范围:全章综合侧试 解答参考时间:90分钟 满分120分)
一、选择题(每小题3分,共30分)
1.“抛一枚均匀硬币,落地后正面朝上”这一事件是( B )
A.必然事件 B.随机事件 C.确定事件 D.不可能事件
2.从只装有4个红球的袋中随机摸出一球,若摸到白球的概率是P1,摸到红球的概率是P2,则( B )
A. P1=1,P2=1 B. P1=0,P2=1 C. P1=0,P2= D. P1=P2=
3.如图,一个可以启由转动的转盘被等分成6个扇形区域,并涂上了相应的颜色,转动转盘,转盘停止后,指针指向蓝色区域的概率是( B )
A. B. C. D.
4.掷一个质地均匀的正方体般子,当般子停止后,朝上一面的点数为5的概率是( C )
A.1 B. C. D.0
5.在抛掷一枚硬币的实验中,某一组做了500次试验,其出现正面的频率是49. 6%,可以推知出现正面的次数是( A )
A.248 B.250 C.258 D.无法确定
6.在一个不透明的袋子中装有除颜色外其它均相同的3个红球和2个白球,从中任意摸出一个球,则摸出白球的概率是( B )
A. B. C. D.
7.一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有6个黄球.每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色 后再放回盒子,通过大量重复摸球实验后发现,摸到黄球的频率稳定在30%,那么可以推算出n大约是( D )
A.6 B. 10 C. 18 D. 20
8.经过某十字路口的汽车,可能直行,也可能左转或者右转.如果这三种可能性大小相同,则经过这个十字路口的两辆汽车都直行的概率是( D )
A. B. C. D.
9.如图,转动两个转盘,当指针所指的数之和为奇数时,小明胜,否则小亮胜,则小明获胜的概率是( D )
A. B. C. D.
10.一个盒子里有完全相同的三个小球,球上分别标有数字-1,1,2.随机摸出一个小球(不放回),其数字记为p,再随机摸出另一个小球,其数字记为q,则满足关于x的方程x2+px+q=0有实数根的概率是( A )
A. B. C. D.
二、填空题(每小题3分,共18分)
11.如图,是一副普通扑克牌中的13张黑桃牌,将它们洗匀后正面向下放在桌子上,从中任意抽取一张,则抽出的牌点数小于9的概率为.
12.在英语句子“Wish you success!"(祝你成功!)中任选一个字母,这个字母为“s”的概率是.
13.在一个不透明的口袋中有颜色不同的红、自两种小球,其中红球3只,白球n只,若从袋中任取一个球,摸出白球的概率为,则n= 9
14.为了估计不透明的袋子里装有多少白球,先从袋中摸出10个球都做上标记,然后放回袋中去,充分摇匀后再摸出10个球,发现其中有一个球有标记,那么你估计袋中大约有100个白球.
15.现有四张分别标有数字1,2,3,4的卡片,它们除数字外完全相同,把卡片背面朝上洗匀,从中随机抽取一张后放回,再背面朝上洗匀,从中随机抽取一张,则两次抽出的卡片所标数字不同的概率是
16.如图,第(1)个图有1个黑球;第(2)个图为一3个同样大小球叠成的图形,最下一层的2个球为黑色,其余为白色;第(3)个图为6个同样大小球叠成的图形,最下一层的3个球为黑色,其余为白色;则从第(n)个图中随机取出一个球是黑球的概率是
三、解答题(共8题,共72分)
17.(本题8分)布袋中装有1个红球,2个白球,3个黑球,它们除颜色外完全相同,从袋中任意摸出一个球,求摸出的球是白球的概率.
解:
18.(本题8分)一个口袋中有3个大小相同的小球,球面上分别写有数字1,2,3,从袋中随机地摸出一个小球,记录下数字后放回,再随机地摸出一个小球.
(1)请用树形图或列表法中的一种,列举出两次摸出的球上数字的所有可能结果;
(2)求两次摸出的球上的数字和为偶数的概率.
解:(1)共有9种等可能的结果;
(2)由(1)得:两次摸出的球上的数字和为偶数的有5种情况,
∴两次摸出的球上的数字和为偶数的概率为:.
19.(本题8分)商店只有雪碧、可乐、果汁、奶汁四种饮料,每种饮料数量充足,某同学去该店购买饮料,每种饮料被选中的可能性相同.
(1)若他去买一瓶饮料,则他买到奶汁的概率是 ;
(2)若他两次去买饮料,每次买一瓶,且两次所买饮料品种不同,请用树状图或列表法求出他恰好买到雪碧和奶汁的概率.
解:(1)
(2)∴共有12种等可能的结果,他恰好买到雪碧和奶汁的有2种情况,
∴他恰好买到雪碧和奶汁的概率为.
20.(本题8分)在一个不透明的口袋中装有红、白、黑三种颜色的小球若干个,它们只有颜色不同,其中有白球2个、黑球1个。己知从中任意摸出1个球得白球的概率为.
(1)求口袋中有多少个红球;
(2)求从袋中一次摸出2个球,得一红一白的概率.(要求画出树状图)
解:(1)设袋中有x个红球,据题意得,解得x=1,∴口袋中有红球1个;
(2)P(摸得一红一白)=
21.(本题8分)“阳光体育”运动关乎每个学生未来的幸福生活,今年五月,我市某校开展了以“阳光体育我是冠军”为主题的一分钟限时跳绳比赛,要求每个班选2-3名选手参赛,现将80名选手比赛成绩(单位:次/分钟)进行统计.绘制成频数分布直方图,如图所示.
(1)图中a值为 4 ;
(2)将跳绳次数在160—190的选手依次记为A1,A2,…An,从中随机抽取两名选手作经一验交流,请用画树状图或列表法求恰好抽取到的选手是A1和A2的概率.
解:(1)根据题意得:a=80-8-40-28=4,故答案为:4;
(2)画树状图略.∵共有12种等可能的结果,恰好抽取到的选手A1和A2的有2种情况,
∴恰好抽取到的选手A1和A2的概率为:.
22;(本题10分)(1)甲、乙、丙、丁四人做传球游戏:第一次由甲将球随机传给乙、丙、丁的某一人,从第二次起,每一次都由持球者将球再随机传给其他三人的某一人·求第二次传球后球回到甲手里的概率.(请用“画树状图"或“列表”等方式给分析过程)
(2)如果甲跟另外n(n>2)个人做(1)同样的游戏,那么第三次传球后球回到甲手里的概率是.(请直接写出结果).
解:(1)每树状图略.共有9种等可能的结果,其符合要求的结果有3种,
∴P(第2次传球后球回到甲手里)=.
(2)
23.(本题10分)某校组织了一次初三科技小制作比赛,有A,B,C,D四个班共提供了100件参赛作品.C班提供的参赛作品的获奖率为50%,其他几个班的参赛作品情况及获奖情况绘制在下列图1和图2两幅尚不完整的统计图中.
(1)B班参赛作品有多少件
(2)请你将图②的统计图补充完整;
(3)通过计算说明,哪个班的获奖率高
(4)将写有A,B,C,D四个字母的完全相同的卡片放人箱中,从中一次随机抽出两张卡片,求抽到A,B两班的概率.
解:(1)100×(1-35% -20%-20% )=25(件),答:B班参赛作品有25件;
(2)∵C班提供的参赛作品的获奖率为50%,
∴C班的参赛作品的获奖数量为:100×20%×50%=10(件),画图略.
(3) A班的获奖率为:,
B班的获奖率为:,
C班的获奖率为:50%,
D班的获奖率为:,故B班的获奖率高;
(4) 画图略,一共有12种等可能的情况,符合题意的有2种情况,则从中一次随机抽出两张卡片,求抽到A,B两班的概率为:.
24.(本题12分)已知M(x,y)是平面直角坐标系xOy中的点,其中x是从1,2,3三个数中任取的一个数,y是从1,2,3,4四个数中任取的一个数.
(1)计算由x;y确定的点M(x,y)在函数y=-x+5的图象上的概率;
(2)小明和小红约定做一个游戏,其规则为:若x,y满足xy>6则小明胜,若x,y满足xy<6则小红胜,这个游戏公平吗 说明理由.若不公平,请写出公平的游戏规则;
(3)定义“点M(x,y)在直线x+ y=n上”为事件A(2≤n≤7, n为整数),则当A的概率最大时,n的所有可能的值为 .(不需要解答过程)
解:(1)
(2) P(小明胜)=,P(小红胜)=,
游戏规则改为:若x、y,满足xy>6,,则小明得7分,若x,y满足xy<6,则小红得3分;
(3)4,5
21世纪教育网(www.21cnjy.com)
23.九年级数学(上)第25章《概率初步》单元检测题
(测试范围:全章综合侧试 解答参考时间:90分钟 满分120分)
一、选择题(每小题3分,共30分)
1.“抛一枚均匀硬币,落地后正面朝上”这一事件是( )
A.必然事件 B.随机事件 C.确定事件 D.不可能事件
2.从只装有4个红球的袋中随机摸出一球,若摸到白球的概率是P1,摸到红球的概率是P2,则( )
A. P1=1,P2=1 B. P1=0,P2=1 C. P1=0,P2= D. P1=P2=
3.如图,一个可以启由转动的转盘被等分成6个扇形区域,并涂上了相应的颜色,转动转盘,转盘停止后,指针指向蓝色区域的概率是( )
A. B. C. D.
4.掷一个质地均匀的正方体般子,当般子停止后,朝上一面的点数为5的概率是( )
A.1 B. C. D.0
5.在抛掷一枚硬币的实验中,某一组做了500次试验,其出现正面的频率是49. 6%,可以推知出现正面的次数是( )
A.248 B.250 C.258 D.无法确定
6.在一个不透明的袋子中装有除颜色外其它均相同的3个红球和2个白球,从中任意摸出一个球,则摸出白球的概率是( )
A. B. C. D.
7.一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有6个黄球.每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色 后再放回盒子,通过大量重复摸球实验后发现,摸到黄球的频率稳定在30%,那么可以推算出n大约是( )
A.6 B. 10 C. 18 D. 20
8.经过某十字路口的汽车,可能直行,也可能左转或者右转.如果这三种可能性大小相同,则经过这个十字路口的两辆汽车都直行的概率是( )
A. B. C. D.
9.如图,转动两个转盘,当指针所指的数之和为奇数时,小明胜,否则小亮胜,则小明获胜的概率是( )
A. B. C. D.
10.一个盒子里有完全相同的三个小球,球上分别标有数字-1,1,2.随机摸出一个小球(不放回),其数字记为p,再随机摸出另一个小球,其数字记为q,则满足关于x的方程x2+px+q=0有实数根的概率是( )
A. B. C. D.
二、填空题(每小题3分,共18分)
11.如图,是一副普通扑克牌中的13张黑桃牌,将它们洗匀后正面向下放在桌子上,从中任意抽取一张,则抽出的牌点数小于9的概率为 .
12.在英语句子“Wish you success!"(祝你成功!)中任选一个字母,这个字母为“s”的概率是 .
13.在一个不透明的口袋中有颜色不同的红、自两种小球,其中红球3只,白球n只,若从袋中任取一个球,摸出白球的概率为,则n= .
14.为了估计不透明的袋子里装有多少白球,先从袋中摸出10个球都做上标记,然后放回袋中去,充分摇匀后再摸出10个球,发现其中有一个球有标记,那么你估计袋中大约有100个白球.
15.现有四张分别标有数字1,2,3,4的卡片,它们除数字外完全相同,把卡片背面朝上洗匀,从中随机抽取一张后放回,再背面朝上洗匀,从中随机抽取一张,则两次抽出的卡片所标数字不同的概率是 .
16.如图,第(1)个图有1个黑球;第(2)个图为一3个同样大小球叠成的图形,最下一层的2个球为黑色,其余为白色;第(3)个图为6个同样大小球叠成的图形,最下一层的3个球为黑色,其余为白色;则从第(n)个图中随机取出一个球是黑球的概率是 .
三、解答题(共8题,共72分)
17.(本题8分)布袋中装有1个红球,2个白球,3个黑球,它们除颜色外完全相同,从袋中任意摸出一个球,求摸出的球是白球的概率.
18.(本题8分)一个口袋中有3个大小相同的小球,球面上分别写有数字1,2,3,从袋中随机地摸出一个小球,记录下数字后放回,再随机地摸出一个小球.
(1)请用树形图或列表法中的一种,列举出两次摸出的球上数字的所有可能结果;
(2)求两次摸出的球上的数字和为偶数的概率.
19.(本题8分)商店只有雪碧、可乐、果汁、奶汁四种饮料,每种饮料数量充足,某同学去该店购买饮料,每种饮料被选中的可能性相同.
(1)若他去买一瓶饮料,则他买到奶汁的概率是 ;
(2)若他两次去买饮料,每次买一瓶,且两次所买饮料品种不同,请用树状图或列表法求出他恰好买到雪碧和奶汁的概率.
20.(本题8分)在一个不透明的口袋中装有红、白、黑三种颜色的小球若干个,它们只有颜色不同,其中有白球2个、黑球1个。己知从中任意摸出1个球得白球的概率为.
(1)求口袋中有多少个红球;
(2)求从袋中一次摸出2个球,得一红一白的概率.(要求画出树状图)
21.(本题8分)“阳光体育”运动关乎每个学生未来的幸福生活,今年五月,我市某校开展了以“阳光体育我是冠军”为主题的一分钟限时跳绳比赛,要求每个班选2-3名选手参赛,现将80名选手比赛成绩(单位:次/分钟)进行统计.绘制成频数分布直方图,如图所示.
(1)图中a值为 ;
(2)将跳绳次数在160—190的选手依次记为A1,A2,…An,从中随机抽取两名选手作经一验交流,请用画树状图或列表法求恰好抽取到的选手是A1和A2的概率.
22;(本题10分)(1)甲、乙、丙、丁四人做传球游戏:第一次由甲将球随机传给乙、丙、丁的某一人,从第二次起,每一次都由持球者将球再随机传给其他三人的某一人·求第二次传球后球回到甲手里的概率.(请用“画树状图"或“列表”等方式给分析过程)
(2)如果甲跟另外n(n>2)个人做(1)同样的游戏,那么第三次传球后球回到甲手里的概率是.(请直接写出结果).
23.(本题10分)某校组织了一次初三科技小制作比赛,有A,B,C,D四个班共提供了100件参赛作品.C班提供的参赛作品的获奖率为50%,其他几个班的参赛作品情况及获奖情况绘制在下列图1和图2两幅尚不完整的统计图中.
(1)B班参赛作品有多少件
(2)请你将图②的统计图补充完整;
(3)通过计算说明,哪个班的获奖率高
(4)将写有A,B,C,D四个字母的完全相同的卡片放人箱中,从中一次随机抽出两张卡片,求抽到A,B两班的概率.
24.(本题12分)已知M(x,y)是平面直角坐标系xOy中的点,其中x是从1,2,3三个数中任取的一个数,y是从1,2,3,4四个数中任取的一个数.
(1)计算由x;y确定的点M(x,y)在函数y=-x+5的图象上的概率;
(2)小明和小红约定做一个游戏,其规则为:若x,y满足xy>6则小明胜,若x,y满足xy<6则小红胜,这个游戏公平吗 说明理由.若不公平,请写出公平的游戏规则;
(3)定义“点M(x,y)在直线x+ y=n上”为事件A(2≤n≤7, n为整数),则当A的概率最大时,n的所有可能的值为 .(不需要解答过程)
23.九年级数学(上)第25章《概率初步》单元检测题
(测试范围:全章综合侧试 解答参考时间:90分钟 满分120分)
一、选择题(每小题3分,共30分)
1.“抛一枚均匀硬币,落地后正面朝上”这一事件是( B )
A.必然事件 B.随机事件 C.确定事件 D.不可能事件
2.从只装有4个红球的袋中随机摸出一球,若摸到白球的概率是P1,摸到红球的概率是P2,则( B )
A. P1=1,P2=1 B. P1=0,P2=1 C. P1=0,P2= D. P1=P2=
3.如图,一个可以启由转动的转盘被等分成6个扇形区域,并涂上了相应的颜色,转动转盘,转盘停止后,指针指向蓝色区域的概率是( B )
A. B. C. D.
4.掷一个质地均匀的正方体般子,当般子停止后,朝上一面的点数为5的概率是( C )
A.1 B. C. D.0
5.在抛掷一枚硬币的实验中,某一组做了500次试验,其出现正面的频率是49. 6%,可以推知出现正面的次数是( A )
A.248 B.250 C.258 D.无法确定
6.在一个不透明的袋子中装有除颜色外其它均相同的3个红球和2个白球,从中任意摸出一个球,则摸出白球的概率是( B )
A. B. C. D.
7.一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有6个黄球.每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色 后再放回盒子,通过大量重复摸球实验后发现,摸到黄球的频率稳定在30%,那么可以推算出n大约是( D )
A.6 B. 10 C. 18 D. 20
8.经过某十字路口的汽车,可能直行,也可能左转或者右转.如果这三种可能性大小相同,则经过这个十字路口的两辆汽车都直行的概率是( D )
A. B. C. D.
9.如图,转动两个转盘,当指针所指的数之和为奇数时,小明胜,否则小亮胜,则小明获胜的概率是( D )
A. B. C. D.
10.一个盒子里有完全相同的三个小球,球上分别标有数字-1,1,2.随机摸出一个小球(不放回),其数字记为p,再随机摸出另一个小球,其数字记为q,则满足关于x的方程x2+px+q=0有实数根的概率是( A )
A. B. C. D.
二、填空题(每小题3分,共18分)
11.如图,是一副普通扑克牌中的13张黑桃牌,将它们洗匀后正面向下放在桌子上,从中任意抽取一张,则抽出的牌点数小于9的概率为.
12.在英语句子“Wish you success!"(祝你成功!)中任选一个字母,这个字母为“s”的概率是.
13.在一个不透明的口袋中有颜色不同的红、自两种小球,其中红球3只,白球n只,若从袋中任取一个球,摸出白球的概率为,则n= 9
14.为了估计不透明的袋子里装有多少白球,先从袋中摸出10个球都做上标记,然后放回袋中去,充分摇匀后再摸出10个球,发现其中有一个球有标记,那么你估计袋中大约有100个白球.
15.现有四张分别标有数字1,2,3,4的卡片,它们除数字外完全相同,把卡片背面朝上洗匀,从中随机抽取一张后放回,再背面朝上洗匀,从中随机抽取一张,则两次抽出的卡片所标数字不同的概率是
16.如图,第(1)个图有1个黑球;第(2)个图为一3个同样大小球叠成的图形,最下一层的2个球为黑色,其余为白色;第(3)个图为6个同样大小球叠成的图形,最下一层的3个球为黑色,其余为白色;则从第(n)个图中随机取出一个球是黑球的概率是
三、解答题(共8题,共72分)
17.(本题8分)布袋中装有1个红球,2个白球,3个黑球,它们除颜色外完全相同,从袋中任意摸出一个球,求摸出的球是白球的概率.
解:
18.(本题8分)一个口袋中有3个大小相同的小球,球面上分别写有数字1,2,3,从袋中随机地摸出一个小球,记录下数字后放回,再随机地摸出一个小球.
(1)请用树形图或列表法中的一种,列举出两次摸出的球上数字的所有可能结果;
(2)求两次摸出的球上的数字和为偶数的概率.
解:(1)共有9种等可能的结果;
(2)由(1)得:两次摸出的球上的数字和为偶数的有5种情况,
∴两次摸出的球上的数字和为偶数的概率为:.
19.(本题8分)商店只有雪碧、可乐、果汁、奶汁四种饮料,每种饮料数量充足,某同学去该店购买饮料,每种饮料被选中的可能性相同.
(1)若他去买一瓶饮料,则他买到奶汁的概率是 ;
(2)若他两次去买饮料,每次买一瓶,且两次所买饮料品种不同,请用树状图或列表法求出他恰好买到雪碧和奶汁的概率.
解:(1)
(2)∴共有12种等可能的结果,他恰好买到雪碧和奶汁的有2种情况,
∴他恰好买到雪碧和奶汁的概率为.
20.(本题8分)在一个不透明的口袋中装有红、白、黑三种颜色的小球若干个,它们只有颜色不同,其中有白球2个、黑球1个。己知从中任意摸出1个球得白球的概率为.
(1)求口袋中有多少个红球;
(2)求从袋中一次摸出2个球,得一红一白的概率.(要求画出树状图)
解:(1)设袋中有x个红球,据题意得,解得x=1,∴口袋中有红球1个;
(2)P(摸得一红一白)=
21.(本题8分)“阳光体育”运动关乎每个学生未来的幸福生活,今年五月,我市某校开展了以“阳光体育我是冠军”为主题的一分钟限时跳绳比赛,要求每个班选2-3名选手参赛,现将80名选手比赛成绩(单位:次/分钟)进行统计.绘制成频数分布直方图,如图所示.
(1)图中a值为 4 ;
(2)将跳绳次数在160—190的选手依次记为A1,A2,…An,从中随机抽取两名选手作经一验交流,请用画树状图或列表法求恰好抽取到的选手是A1和A2的概率.
解:(1)根据题意得:a=80-8-40-28=4,故答案为:4;
(2)画树状图略.∵共有12种等可能的结果,恰好抽取到的选手A1和A2的有2种情况,
∴恰好抽取到的选手A1和A2的概率为:.
22;(本题10分)(1)甲、乙、丙、丁四人做传球游戏:第一次由甲将球随机传给乙、丙、丁的某一人,从第二次起,每一次都由持球者将球再随机传给其他三人的某一人·求第二次传球后球回到甲手里的概率.(请用“画树状图"或“列表”等方式给分析过程)
(2)如果甲跟另外n(n>2)个人做(1)同样的游戏,那么第三次传球后球回到甲手里的概率是.(请直接写出结果).
解:(1)每树状图略.共有9种等可能的结果,其符合要求的结果有3种,
∴P(第2次传球后球回到甲手里)=.
(2)
23.(本题10分)某校组织了一次初三科技小制作比赛,有A,B,C,D四个班共提供了100件参赛作品.C班提供的参赛作品的获奖率为50%,其他几个班的参赛作品情况及获奖情况绘制在下列图1和图2两幅尚不完整的统计图中.
(1)B班参赛作品有多少件
(2)请你将图②的统计图补充完整;
(3)通过计算说明,哪个班的获奖率高
(4)将写有A,B,C,D四个字母的完全相同的卡片放人箱中,从中一次随机抽出两张卡片,求抽到A,B两班的概率.
解:(1)100×(1-35% -20%-20% )=25(件),答:B班参赛作品有25件;
(2)∵C班提供的参赛作品的获奖率为50%,
∴C班的参赛作品的获奖数量为:100×20%×50%=10(件),画图略.
(3) A班的获奖率为:,
B班的获奖率为:,
C班的获奖率为:50%,
D班的获奖率为:,故B班的获奖率高;
(4) 画图略,一共有12种等可能的情况,符合题意的有2种情况,则从中一次随机抽出两张卡片,求抽到A,B两班的概率为:.
24.(本题12分)已知M(x,y)是平面直角坐标系xOy中的点,其中x是从1,2,3三个数中任取的一个数,y是从1,2,3,4四个数中任取的一个数.
(1)计算由x;y确定的点M(x,y)在函数y=-x+5的图象上的概率;
(2)小明和小红约定做一个游戏,其规则为:若x,y满足xy>6则小明胜,若x,y满足xy<6则小红胜,这个游戏公平吗 说明理由.若不公平,请写出公平的游戏规则;
(3)定义“点M(x,y)在直线x+ y=n上”为事件A(2≤n≤7, n为整数),则当A的概率最大时,n的所有可能的值为 .(不需要解答过程)
解:(1)
(2) P(小明胜)=,P(小红胜)=,
游戏规则改为:若x、y,满足xy>6,,则小明得7分,若x,y满足xy<6,则小红得3分;
(3)4,5
21世纪教育网(www.21cnjy.com)
同课章节目录
