课时训练:圆的面积(同步练习)数学六年级上册北师大版(含答案)
文档属性
| 名称 | 课时训练:圆的面积(同步练习)数学六年级上册北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-17 21:43:04 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
课时训练:圆的面积(同步练习)数学六年级上册北师大版
一、选择题
1.用三根长度都是3.14 dm长的铁丝,分别围成长方形、正方形和圆,( )的面积最大.
A.长方形 B.圆 C.正方形 D.一样大
2.一钟表的时针长5厘米,它一天所扫过部分的面积是( )。
A.78.5平方厘米 B.31.4平方厘米 C.157平方厘米
3.一个圆的周长扩大2倍,它的面积就扩大( )倍。
A.2 B.4 C.
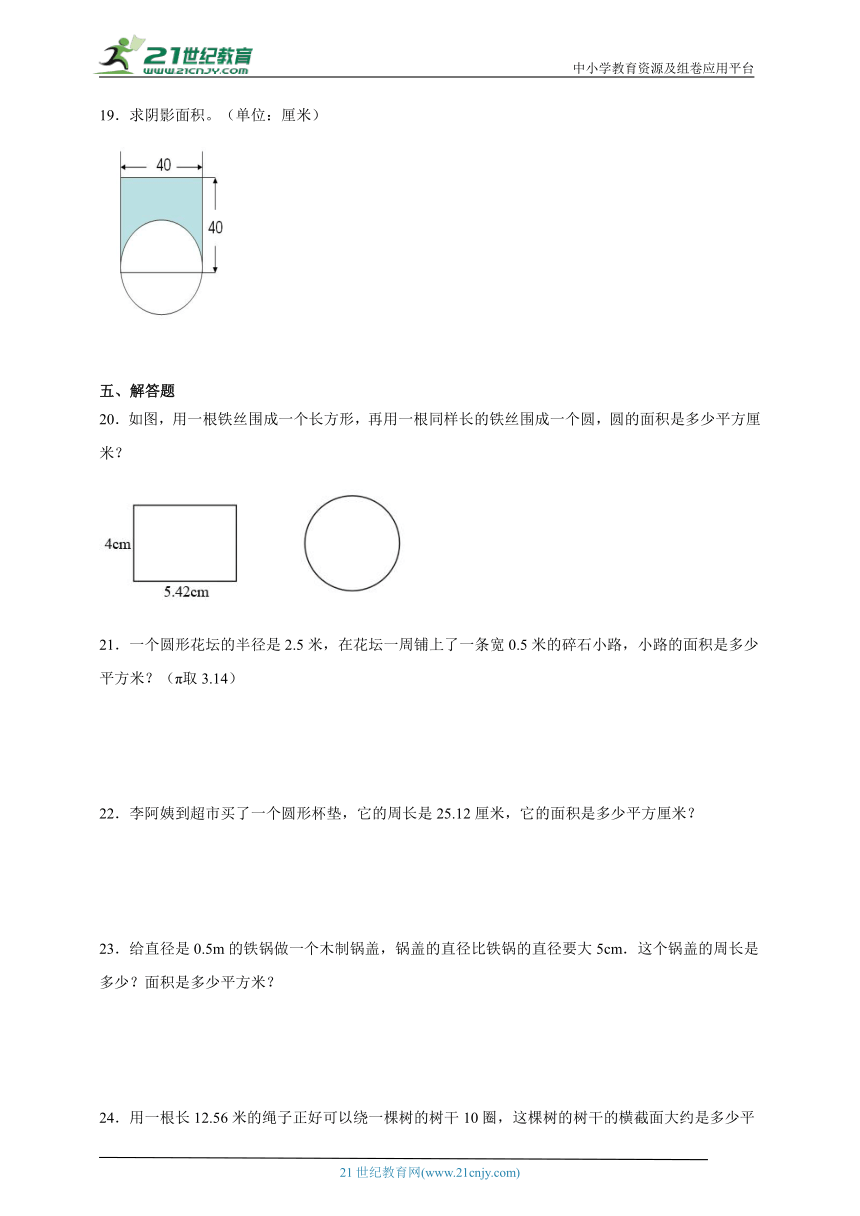
4.如图:4个圆的直径都是6cm,图中阴影部分面积是( )cm2。
A.36 B.24 C.16 D.9
5.把一个圆等分成若干个小扇形后拼成一个近似的长方形,周长增加了4厘米,这个圆的面积是( )平方厘米。
A.3.14 B.6.28 C.12.56
6.某天晚饭后,小雅以每分钟62.8米的速度绕圆形体育场的外边沿走了一圈,用了5分钟,这个体育场的占地面积是( )平方米。
A.5024 B.5652 C.7850 D.9420
二、填空题
7.如图,半圆的半径是( )cm,直径是( )cm,半圆的面积是( )cm2。
8.小红沿着一个圆形花坛的周围走了两圈,共走了251.2米。这个圆形花坛的直径是( )米,面积是( )平方米。
9.在边长为6厘米的正方形内画一个最大的圆,那么这个圆的直径为( )厘米,这个圆的面积为( )平方厘米.
10.从一张长10m,宽6cm的长方形纸上剪一个最大的圆,剩下的面积为( )平方厘米。
11.一块圆形桌布,半径是6分米,这块桌布的面积是( )平方分米,如果在它的边沿缝上花边,花边的长度是( )分米。
12.把一个圆切拼成一个近似的长方形,量得这个长方形的宽是2厘米,则圆的直径是( )厘米,长方形的长是( )厘米。
三、判断题
13.当圆的半径等于2cm时,这个圆的周长和面积相等。( )
14.如图是我国珍贵的历史文化遗产《易经》中的一个主要图形﹣﹣﹣太极图,它是数形结合的光辉典范.图中阴阳(即圈内黑白)两部分的面积相等.( )
15.一个圆的半径是2厘米,它的周长是12.56厘米,面积是12.56平方厘米,它的周长和面积相等.( )
16.一个圆环,大圆的半径是10厘米,小圆的直径是8厘米,圆环的面积是36π平方厘米。( )
17.如图中正方形的面积是10cm2,则圆的面积是314cm2。( )
四、图形计算
18.求下图中阴影部分的面积。
19.求阴影面积。(单位:厘米)
五、解答题
20.如图,用一根铁丝围成一个长方形,再用一根同样长的铁丝围成一个圆,圆的面积是多少平方厘米?
21.一个圆形花坛的半径是2.5米,在花坛一周铺上了一条宽0.5米的碎石小路,小路的面积是多少平方米?(π取3.14)
22.李阿姨到超市买了一个圆形杯垫,它的周长是25.12厘米,它的面积是多少平方厘米?
23.给直径是0.5m的铁锅做一个木制锅盖,锅盖的直径比铁锅的直径要大5cm.这个锅盖的周长是多少?面积是多少平方米?
24.用一根长12.56米的绳子正好可以绕一棵树的树干10圈,这棵树的树干的横截面大约是多少平方米?
参考答案:
1.B
【详解】略
2.C
【分析】由于一天扫过部分的面积,一天时针相当于转了2圈,它的半径是5厘米,根据圆的面积公式:S=πr2,把数代入公式即可求解。
【详解】3.14×5×5×2
=78.5×2
=157(平方厘米)
所以它一天扫过部分的面积是157平方厘米。
故答案为:C
【点睛】本题主要考查圆的面积公式,要注意一天时针会转2圈。
3.B
【分析】圆的周长C=2πr,所以圆的周长扩大2倍,半径就扩大了2倍;圆的面积S=πr2,圆的半径扩大2倍,面积就扩大22倍,据此解答。
【详解】2×2=4
它的面积就扩大4倍。
故选择:B
【点睛】此题考查了圆的周长和面积的综合应用,明确如果半径扩大n倍,那么周长就扩大n倍,面积扩大n2倍。
4.A
【分析】由题意可知,阴影部分是一个边长为6cm的正方形,正方形的面积=边长×边长据此解答。
【详解】图中阴影部分面积:6×6=36(平方厘米)
故答案为:A
【点睛】正确理解图意,掌握正方形的面积公式是解答此题的关键。
5.C
【分析】根据圆面积公式的推导过程可知,把一个圆剪拼成一个近似长方形,这个长方形的长等于圆周长的一半,长方形的宽等于圆的半径,由此可知,长方形的周长比圆的周长增加的4厘米是两条半径的长度,据此可以求出半径,再根据圆的面积公式:S=πr2,把数据代入公式解答。
【详解】4÷2=2(厘米)
3.14×22
=3.14×4
=12.56(平方厘米)
把一个圆等分成若干个小扇形后拼成一个近似的长方形,周长增加了4厘米,这个圆的面积是12.56平方厘米。
故答案为:C
【点睛】本题考查的目的是理解掌握圆面积公式的推导过程及应用。
6.C
【分析】根据速度×时间=路程,用62.8×5即可求出圆周长,然后根据圆周长公式:C=2πr,用圆周长÷2÷3.14即可求出半径,再根据圆面积公式:S=πr2,代入数据解答。
【详解】62.8×5=314(米)
314÷2÷3.14=50(米)
3.14×502
=3.14×2500
=7850(平方米)
这个体育场的占地面积是7850平方米。
故答案为:C
【点睛】本题主要考查了圆面积公式、圆周长公式的灵活应用,要熟练掌握相关公式。
7. 5 10 39.25
【分析】观察图形可知,半圆的半径等于长方形的宽,直径=半径×2,半圆的面积S=πr2÷2,据此解答。
【详解】半圆的半径是5cm,直径是10cm。
3.14×52÷2
=78.5÷2
=39.25(平方厘米)
半圆的面积是39.25平方厘米。
【点睛】此题考查了圆的特征以及面积计算,掌握圆面积计算公式,认真解答即可。
8. 40 1256
【解析】略
9. 6 28.26
【详解】略
10.31.74
【分析】在这个纸上画的最大圆的直径应等于长方形的宽,长方形的宽已知,从而可以求出这个圆的面积,用长方形的面积减圆的面积即可求出剩下的面积。
【详解】6÷2=3(厘米)
3.14×3×3
=9.42×3
=28.26(平方厘米)
10×6-28.26
=60-28.26
=31.74(平方厘米)
【点睛】解答此题的关键是明白:在这个纸板上画的最大圆的直径应等于长方形的宽,据此即可逐步求解。
11. 113.04 37.68
【分析】根据圆的面积公式:S=πr2,用3.14×62即可求出圆面积,根据圆的周长公式:C=2πr,用2×3.14×6即可求出圆周长。
【详解】3.14×62
=3.14×36
=113.04(平方分米)
2×3.14×6=37.68(分米)
这块桌布的面积是113.04平方分米,如果在它的边沿缝上花边,花边的长度是37.68分米。
【点睛】本题主要考查了圆面积、圆周长公式的灵活应用,要熟练掌握相关公式。
12. 4 6.28
【分析】根据圆面积推导公式知:把一个圆切拼成一个近似的长方形,这个近似长方形的长是圆周长的一半,宽是圆的半径,然后根据同圆或等圆中直径是半径的2倍,及圆的周长公式求出近似长方形的长.据此解答。
【详解】(厘米)
(厘米)
把一个圆切拼成一个近似的长方形,量得这个长方形的宽是2厘米,则圆的直径是4厘米,长方形的长是6.28厘米。
【点睛】本题的关键是理解:把一个圆切拼成一个近似的长方形,这个近似长方形的长是圆周长的一半,宽是圆的半径。
13.×
【分析】圆的周长:C=2πr,圆的面积:S=πr2,可以先根据公式计算,再比较。
【详解】当圆的半径等于2cm时,
它的周长是:3.14×2×2=12.56(cm)
它的面积是:3.14×2×2=12.56(cm2)
12.56cm≠12.56cm2,圆的周长和面积是两个不同意义的量,无法比较。
故答案为:×
【点睛】本题主要考查对圆的周长和面积的理解,还要掌握圆的周长和面积公式。
14.√
【详解】略
15.×
【详解】略
16.×
【分析】圆环的面积S=π(R2-r2),带入数据求出面积,比较即可判断。
【详解】8÷2=4(厘米)
π×(102-42)
=π×(100-16)
=π×84
=84π(平方厘米)
所以这个环形的面积是84π平方厘米。
84π≠36π
因此,题干中的计算是错误的。
故答案为:×。
【点睛】本题主要考查圆环面积公式的识记。
17.×
【分析】圆的半径为r,又因正方形的边长等于圆的半径,且正方形的面积是10平方厘米,即r2=10,进而利用圆的面积公式即可求解。
【详解】圆的半径为r,由题意得:r2=10,
所以圆的面积为:
πr2=10π
=10×3.14
=31.4(平方厘米)
故答案为:×。
【点睛】解答此题的关键是明白:圆的半径等于正方形的边长。
18.6.88cm2
【分析】根据图示,该阴影的面积等于长方形面积减去半圆面积;长方体面积公式:S=ab,圆的面积公式:S=πr2。
【详解】4×2×4-3.14×42÷2
=8×4-3.14×42÷2
=32-3.14×16÷2
=32-50.24÷2
=32-25.12
=6.88(cm2)
这个图形的面积是6.88 cm2。
19.972平方厘米
【分析】由图可知,阴影部分的面积=正方形的面积-半圆的面积,其中,正方形的边长是40厘米,半圆的直径是40厘米,据此解答。
【详解】40×40-3.14×(40÷2)2÷2
=1600-628
=972(平方厘米)
20.28.26平方厘米
【分析】长方形的周长=(长+宽)×2,长方形周长=圆的周长,圆的周长÷π÷2=圆的半径,π×半径的平方=圆的面积,据此解答。
【详解】(4+5.42)×2
=9.42×2
=18.84(厘米)
3.14×(18.84÷3.14÷2)2
=3.14×9
=28.26(平方厘米)
答:圆的面积是28.26平方厘米。
【点睛】解答此题的关键是计算出长方形的周长也是圆的周长,然后再根据圆的周长公式计算出圆的半径即可。
21.8.635平方米
【分析】根据题意,求小路的面积,就是求圆环的面积,大圆的半径=圆心花坛的半径+小路的宽,小圆的半径就是花坛的半径;根据圆环的面积公式:面积=π×(大圆半径2-小圆半径2),代入数据,即可解答。
【详解】3.14×[(2.5+0.5)2-2.52]
=3.14×[32-6.25]
=3.14×[9-6.25]
=3.14×2.75
=8.635(平方米)
答:小路的面积是8.635平方米。
【点睛】利用圆环的面积公式进行解答,关键是熟记公式。
22.50.24平方厘米
【详解】25.12÷2÷3.14=4(厘米)
3.14×42=50.24(平方厘米)
23.172.7厘米;0.24平方米
【详解】0.5m=50cm 50+5=55cm
C=πd=3.14×55=172.7cm
S=πr =3.14×() =2374.625cm ≈0.24m
24.0.1256平方米
【详解】12.56÷10÷3.14÷2=0.2(米)
3.14×0.22=0.1256(平方米)
答:这棵树的树干的横截面大约是0.1256平方米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
课时训练:圆的面积(同步练习)数学六年级上册北师大版
一、选择题
1.用三根长度都是3.14 dm长的铁丝,分别围成长方形、正方形和圆,( )的面积最大.
A.长方形 B.圆 C.正方形 D.一样大
2.一钟表的时针长5厘米,它一天所扫过部分的面积是( )。
A.78.5平方厘米 B.31.4平方厘米 C.157平方厘米
3.一个圆的周长扩大2倍,它的面积就扩大( )倍。
A.2 B.4 C.
4.如图:4个圆的直径都是6cm,图中阴影部分面积是( )cm2。
A.36 B.24 C.16 D.9
5.把一个圆等分成若干个小扇形后拼成一个近似的长方形,周长增加了4厘米,这个圆的面积是( )平方厘米。
A.3.14 B.6.28 C.12.56
6.某天晚饭后,小雅以每分钟62.8米的速度绕圆形体育场的外边沿走了一圈,用了5分钟,这个体育场的占地面积是( )平方米。
A.5024 B.5652 C.7850 D.9420
二、填空题
7.如图,半圆的半径是( )cm,直径是( )cm,半圆的面积是( )cm2。
8.小红沿着一个圆形花坛的周围走了两圈,共走了251.2米。这个圆形花坛的直径是( )米,面积是( )平方米。
9.在边长为6厘米的正方形内画一个最大的圆,那么这个圆的直径为( )厘米,这个圆的面积为( )平方厘米.
10.从一张长10m,宽6cm的长方形纸上剪一个最大的圆,剩下的面积为( )平方厘米。
11.一块圆形桌布,半径是6分米,这块桌布的面积是( )平方分米,如果在它的边沿缝上花边,花边的长度是( )分米。
12.把一个圆切拼成一个近似的长方形,量得这个长方形的宽是2厘米,则圆的直径是( )厘米,长方形的长是( )厘米。
三、判断题
13.当圆的半径等于2cm时,这个圆的周长和面积相等。( )
14.如图是我国珍贵的历史文化遗产《易经》中的一个主要图形﹣﹣﹣太极图,它是数形结合的光辉典范.图中阴阳(即圈内黑白)两部分的面积相等.( )
15.一个圆的半径是2厘米,它的周长是12.56厘米,面积是12.56平方厘米,它的周长和面积相等.( )
16.一个圆环,大圆的半径是10厘米,小圆的直径是8厘米,圆环的面积是36π平方厘米。( )
17.如图中正方形的面积是10cm2,则圆的面积是314cm2。( )
四、图形计算
18.求下图中阴影部分的面积。
19.求阴影面积。(单位:厘米)
五、解答题
20.如图,用一根铁丝围成一个长方形,再用一根同样长的铁丝围成一个圆,圆的面积是多少平方厘米?
21.一个圆形花坛的半径是2.5米,在花坛一周铺上了一条宽0.5米的碎石小路,小路的面积是多少平方米?(π取3.14)
22.李阿姨到超市买了一个圆形杯垫,它的周长是25.12厘米,它的面积是多少平方厘米?
23.给直径是0.5m的铁锅做一个木制锅盖,锅盖的直径比铁锅的直径要大5cm.这个锅盖的周长是多少?面积是多少平方米?
24.用一根长12.56米的绳子正好可以绕一棵树的树干10圈,这棵树的树干的横截面大约是多少平方米?
参考答案:
1.B
【详解】略
2.C
【分析】由于一天扫过部分的面积,一天时针相当于转了2圈,它的半径是5厘米,根据圆的面积公式:S=πr2,把数代入公式即可求解。
【详解】3.14×5×5×2
=78.5×2
=157(平方厘米)
所以它一天扫过部分的面积是157平方厘米。
故答案为:C
【点睛】本题主要考查圆的面积公式,要注意一天时针会转2圈。
3.B
【分析】圆的周长C=2πr,所以圆的周长扩大2倍,半径就扩大了2倍;圆的面积S=πr2,圆的半径扩大2倍,面积就扩大22倍,据此解答。
【详解】2×2=4
它的面积就扩大4倍。
故选择:B
【点睛】此题考查了圆的周长和面积的综合应用,明确如果半径扩大n倍,那么周长就扩大n倍,面积扩大n2倍。
4.A
【分析】由题意可知,阴影部分是一个边长为6cm的正方形,正方形的面积=边长×边长据此解答。
【详解】图中阴影部分面积:6×6=36(平方厘米)
故答案为:A
【点睛】正确理解图意,掌握正方形的面积公式是解答此题的关键。
5.C
【分析】根据圆面积公式的推导过程可知,把一个圆剪拼成一个近似长方形,这个长方形的长等于圆周长的一半,长方形的宽等于圆的半径,由此可知,长方形的周长比圆的周长增加的4厘米是两条半径的长度,据此可以求出半径,再根据圆的面积公式:S=πr2,把数据代入公式解答。
【详解】4÷2=2(厘米)
3.14×22
=3.14×4
=12.56(平方厘米)
把一个圆等分成若干个小扇形后拼成一个近似的长方形,周长增加了4厘米,这个圆的面积是12.56平方厘米。
故答案为:C
【点睛】本题考查的目的是理解掌握圆面积公式的推导过程及应用。
6.C
【分析】根据速度×时间=路程,用62.8×5即可求出圆周长,然后根据圆周长公式:C=2πr,用圆周长÷2÷3.14即可求出半径,再根据圆面积公式:S=πr2,代入数据解答。
【详解】62.8×5=314(米)
314÷2÷3.14=50(米)
3.14×502
=3.14×2500
=7850(平方米)
这个体育场的占地面积是7850平方米。
故答案为:C
【点睛】本题主要考查了圆面积公式、圆周长公式的灵活应用,要熟练掌握相关公式。
7. 5 10 39.25
【分析】观察图形可知,半圆的半径等于长方形的宽,直径=半径×2,半圆的面积S=πr2÷2,据此解答。
【详解】半圆的半径是5cm,直径是10cm。
3.14×52÷2
=78.5÷2
=39.25(平方厘米)
半圆的面积是39.25平方厘米。
【点睛】此题考查了圆的特征以及面积计算,掌握圆面积计算公式,认真解答即可。
8. 40 1256
【解析】略
9. 6 28.26
【详解】略
10.31.74
【分析】在这个纸上画的最大圆的直径应等于长方形的宽,长方形的宽已知,从而可以求出这个圆的面积,用长方形的面积减圆的面积即可求出剩下的面积。
【详解】6÷2=3(厘米)
3.14×3×3
=9.42×3
=28.26(平方厘米)
10×6-28.26
=60-28.26
=31.74(平方厘米)
【点睛】解答此题的关键是明白:在这个纸板上画的最大圆的直径应等于长方形的宽,据此即可逐步求解。
11. 113.04 37.68
【分析】根据圆的面积公式:S=πr2,用3.14×62即可求出圆面积,根据圆的周长公式:C=2πr,用2×3.14×6即可求出圆周长。
【详解】3.14×62
=3.14×36
=113.04(平方分米)
2×3.14×6=37.68(分米)
这块桌布的面积是113.04平方分米,如果在它的边沿缝上花边,花边的长度是37.68分米。
【点睛】本题主要考查了圆面积、圆周长公式的灵活应用,要熟练掌握相关公式。
12. 4 6.28
【分析】根据圆面积推导公式知:把一个圆切拼成一个近似的长方形,这个近似长方形的长是圆周长的一半,宽是圆的半径,然后根据同圆或等圆中直径是半径的2倍,及圆的周长公式求出近似长方形的长.据此解答。
【详解】(厘米)
(厘米)
把一个圆切拼成一个近似的长方形,量得这个长方形的宽是2厘米,则圆的直径是4厘米,长方形的长是6.28厘米。
【点睛】本题的关键是理解:把一个圆切拼成一个近似的长方形,这个近似长方形的长是圆周长的一半,宽是圆的半径。
13.×
【分析】圆的周长:C=2πr,圆的面积:S=πr2,可以先根据公式计算,再比较。
【详解】当圆的半径等于2cm时,
它的周长是:3.14×2×2=12.56(cm)
它的面积是:3.14×2×2=12.56(cm2)
12.56cm≠12.56cm2,圆的周长和面积是两个不同意义的量,无法比较。
故答案为:×
【点睛】本题主要考查对圆的周长和面积的理解,还要掌握圆的周长和面积公式。
14.√
【详解】略
15.×
【详解】略
16.×
【分析】圆环的面积S=π(R2-r2),带入数据求出面积,比较即可判断。
【详解】8÷2=4(厘米)
π×(102-42)
=π×(100-16)
=π×84
=84π(平方厘米)
所以这个环形的面积是84π平方厘米。
84π≠36π
因此,题干中的计算是错误的。
故答案为:×。
【点睛】本题主要考查圆环面积公式的识记。
17.×
【分析】圆的半径为r,又因正方形的边长等于圆的半径,且正方形的面积是10平方厘米,即r2=10,进而利用圆的面积公式即可求解。
【详解】圆的半径为r,由题意得:r2=10,
所以圆的面积为:
πr2=10π
=10×3.14
=31.4(平方厘米)
故答案为:×。
【点睛】解答此题的关键是明白:圆的半径等于正方形的边长。
18.6.88cm2
【分析】根据图示,该阴影的面积等于长方形面积减去半圆面积;长方体面积公式:S=ab,圆的面积公式:S=πr2。
【详解】4×2×4-3.14×42÷2
=8×4-3.14×42÷2
=32-3.14×16÷2
=32-50.24÷2
=32-25.12
=6.88(cm2)
这个图形的面积是6.88 cm2。
19.972平方厘米
【分析】由图可知,阴影部分的面积=正方形的面积-半圆的面积,其中,正方形的边长是40厘米,半圆的直径是40厘米,据此解答。
【详解】40×40-3.14×(40÷2)2÷2
=1600-628
=972(平方厘米)
20.28.26平方厘米
【分析】长方形的周长=(长+宽)×2,长方形周长=圆的周长,圆的周长÷π÷2=圆的半径,π×半径的平方=圆的面积,据此解答。
【详解】(4+5.42)×2
=9.42×2
=18.84(厘米)
3.14×(18.84÷3.14÷2)2
=3.14×9
=28.26(平方厘米)
答:圆的面积是28.26平方厘米。
【点睛】解答此题的关键是计算出长方形的周长也是圆的周长,然后再根据圆的周长公式计算出圆的半径即可。
21.8.635平方米
【分析】根据题意,求小路的面积,就是求圆环的面积,大圆的半径=圆心花坛的半径+小路的宽,小圆的半径就是花坛的半径;根据圆环的面积公式:面积=π×(大圆半径2-小圆半径2),代入数据,即可解答。
【详解】3.14×[(2.5+0.5)2-2.52]
=3.14×[32-6.25]
=3.14×[9-6.25]
=3.14×2.75
=8.635(平方米)
答:小路的面积是8.635平方米。
【点睛】利用圆环的面积公式进行解答,关键是熟记公式。
22.50.24平方厘米
【详解】25.12÷2÷3.14=4(厘米)
3.14×42=50.24(平方厘米)
23.172.7厘米;0.24平方米
【详解】0.5m=50cm 50+5=55cm
C=πd=3.14×55=172.7cm
S=πr =3.14×() =2374.625cm ≈0.24m
24.0.1256平方米
【详解】12.56÷10÷3.14÷2=0.2(米)
3.14×0.22=0.1256(平方米)
答:这棵树的树干的横截面大约是0.1256平方米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
