第一单元长方体和正方体必考题检测卷(单元测试)数学六年级上册苏教版(含答案)
文档属性
| 名称 | 第一单元长方体和正方体必考题检测卷(单元测试)数学六年级上册苏教版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 985.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-17 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第一单元长方体和正方体必考题检测卷(单元测试)数学六年级上册苏教版
一、选择题
1.长方体的长、宽、高都扩大到原来的3倍,则它的体积扩大到原来的( )倍。
A.3 B.9 C.18 D.27
2.下面的平面图中,( )不能折成正方体。
A. B. C.
3.用100立方米的沙子铺在一段长是40米,宽是5米的路上,可以铺( )米厚。
A.0.5 B.0.4 C.2
4.一个矿泉水瓶的容积330( )。
A.升 B.毫升 C.立方米 D.立方分米
5.( )个小正方体可以拼成一个大正方体。
A.27 B.16 C.24 D.4
6.如果正方体和长方体的底面周长相等,高也相等,那么它们的体积( )。
A.正方体大 B.长方体大 C.无法比较
二、填空题
7.1.2L=( )cm3 750dm3=( )m3
3dm28cm2=( )dm2 0.69m3=( )dm3=( )mL
8.一个棱长总和是48厘米的正方体纸箱,它的体积是( ),表面积是( )。
9.一根长9米的方钢,把它横截成3段时,表面积增加了60平方分米,原来方钢的体积是( )立方分米。
10.一个长方体的长、宽、高分别是8cm、5cm和4cm,截去一个最大正方体后,剩下的体积是( )。
11.一个长方体刚好可以切成两个同样的正方体,切开后表面积增加了18cm2,这个长方体的体积是( )cm3。
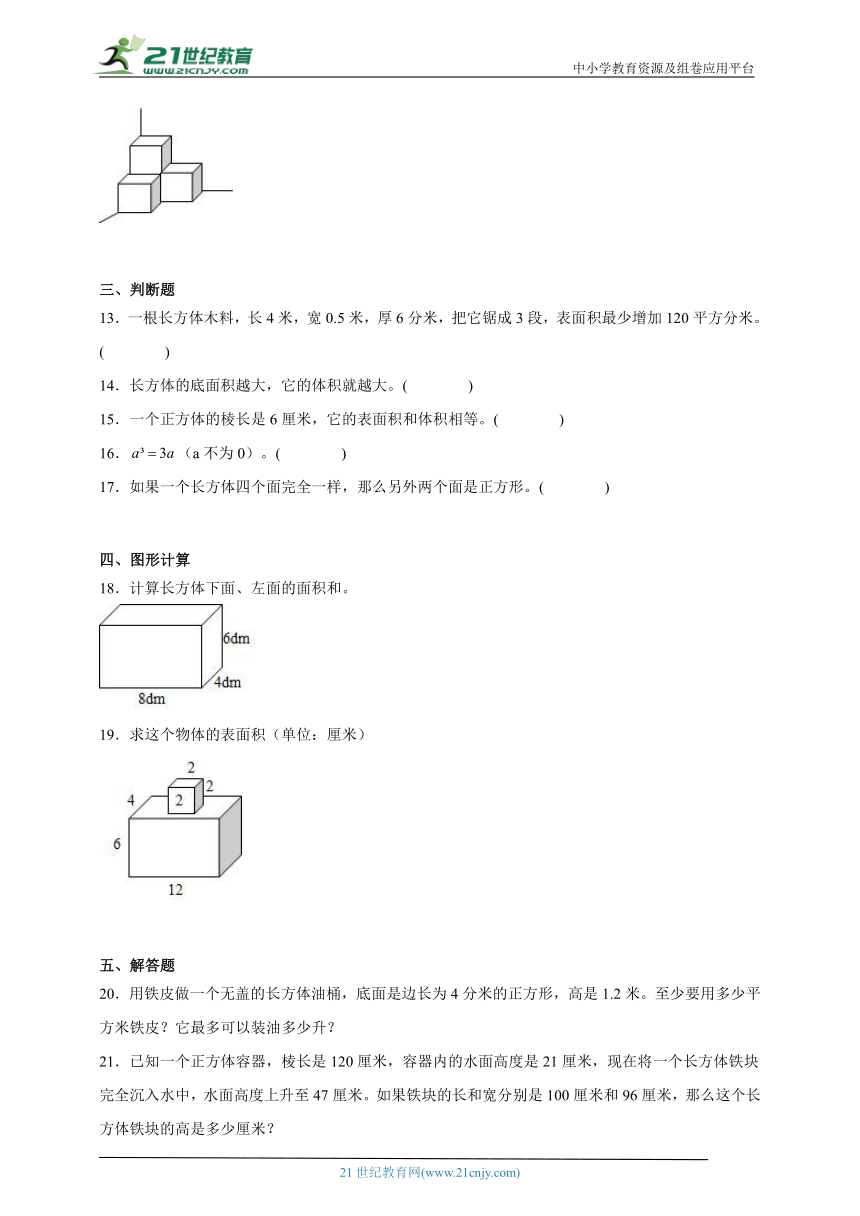
12.(如图)在墙角堆放4个棱长是10分米的正方体纸箱,露在外面的面积是( )平方米。
三、判断题
13.一根长方体木料,长4米,宽0.5米,厚6分米,把它锯成3段,表面积最少增加120平方分米。( )
14.长方体的底面积越大,它的体积就越大。( )
15.一个正方体的棱长是6厘米,它的表面积和体积相等。( )
16.(a不为0)。( )
17.如果一个长方体四个面完全一样,那么另外两个面是正方形。( )
四、图形计算
18.计算长方体下面、左面的面积和。
19.求这个物体的表面积(单位:厘米)
五、解答题
20.用铁皮做一个无盖的长方体油桶,底面是边长为4分米的正方形,高是1.2米。至少要用多少平方米铁皮?它最多可以装油多少升?
21.已知一个正方体容器,棱长是120厘米,容器内的水面高度是21厘米,现在将一个长方体铁块完全沉入水中,水面高度上升至47厘米。如果铁块的长和宽分别是100厘米和96厘米,那么这个长方体铁块的高是多少厘米?
22.某海岛战士为解决岛上淡水缺乏问题,和当地居民共同修建一个长22m,宽10m,深1.8m的淡水蓄水池,这个蓄水池最多可以蓄水多少立方米?
23.一根7.5dm长的长方体木料,把它平均锯成3段,正好分成3个完全一样的正方体,这根木料的体积是多少立方分米?
24.把一根长60厘米的长方体木料锯成3段(如图),表面积比原来增加了120平方厘米。这根木料原来的体积是多少立方厘米?
参考答案:
1.D
【分析】根据长方体的体积=长×宽×高,以及积的变化规律“一个因数不变,另一个因数乘几或除以几(0除外),积也乘(或除以)几”可知,积扩大的倍数等于因数扩大倍数的乘积。
【详解】3×3×3
=9×3
=27
则一个长方体的长、宽、高都扩大到原来的3倍,则它的体积也扩大到原来的27倍。
故答案为:D
【点睛】本题考查长方体体积公式以及积的变化规律的应用。
2.A
【分析】根据正方体展开图的类型,主要分为“1-4-l”型,“2-3-1”型, “2-2-2”型,“3-3”型,据此判断解答即可。
【详解】A.,不属于正方体展开图的类型,所以不能折成正方体;
B.,属于“1-4-l”型,所以能折成正方体;
C.,属于“1-4-l”型,所以能折成正方体。
故答案为:A
【点睛】本题考查正方体的展开图,明确正方体的展开图的特征是解题的关键。
3.A
【分析】将沙子铺在路上,沙子的体积没有变,其中路面的宽为长方体的宽,沙子的厚度为长方体的高,要铺路的长度是长方体的长,根据长方体的体积=长×宽×高,代入数据即可求出铺路的厚度。
【详解】100÷40÷5=0.5(米)
即可以铺0.5米厚。
故答案为:A
【点睛】本题考查长方体体积公式的灵活运用,学生需熟练掌握长方体的高的求法。
4.B
【分析】根据生活经验以及数据的大小,选择合适的计量单位,即可解答。
【详解】一个矿泉水瓶的容积330毫升。
故答案为:B
【点睛】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活的选择。
5.A
【分析】用棱长相等的正方体拼成一个大正方体,小正方体的个数等于每条棱长上切割出的小正方体个数的3次方;据此找出是立方数的数即可得解。
【详解】A.27=33,27个小正方体可以拼成一个大正方体。
B.16=42,16不是立方数,16个小正方体不可以拼成一个大正方体。
C.24不是立方数,24个小正方体不可以拼成一个大正方体。
D.4=22,4不是立方数,4个小正方体不可以拼成一个大正方体。
故答案为:A
【点睛】本题明确小正方体的个数等于每条棱长上切割出的小正方体个数的3次方是关键。
6.A
【分析】当正方形和长方形的周长相等时,正方形的面积大于长方形的面积,正方体和长方体的体积都可以用“底面积×高”来计算,正方体和长方体的高相等,底面积大的体积就比较大,则正方体的体积大于长方体的体积,举例说明即可。
【详解】分析可知,正方体和长方体的底面周长相等时,正方体的底面积大于长方体的底面积,它们的高也相等,则正方体的体积比长方体的体积大,假设正方体和长方体的底面周长为24厘米,高为6厘米。
正方体的体积:24÷4=6(厘米)
6×6×6
=36×6
=216(立方厘米)
长方体的体积:24÷2=12(厘米)
10+2=12(厘米)
长方体的长为10厘米,宽为2厘米。
10×2×6
=20×6
=120(立方厘米)
因为216立方厘米>120立方厘米,所以如果正方体和长方体的底面周长相等,高也相等,那么正方体的体积大于长方体的体积。
故答案为:A
【点睛】熟练掌握并灵活运用长方体和正方体的体积计算公式是解答题目的关键。
7. 1200 0.75 3.08 690 690000
【分析】1L=1000mL,1mL=1cm3,1m3=1000dm3,1dm2=100cm2,1L=1dm3,高级单位换算低级单位乘进率,低级单位换算高级单位除以进率,据此解答。
【详解】(1)1.2×1000=1200(mL)
1200mL=1200cm3
(2)750÷1000=0.75(m3)
(3)3dm28cm2=3dm2+8cm2=3dm2+(8÷100)dm2=3dm2+0.08dm2=3.08dm2
(4)0.69×1000=690(dm3)
690dm3=690L
690×1000=690000(mL)
所以,1.2L=1200cm3,750dm3=0.75m3,3dm28cm2=3.08dm2,0.69m3=690dm3=690000mL。
【点睛】本题主要考查单位换算,熟记单位之间的进率和高低级单位之间转化的方法是解答题目的关键。
8. 64立方厘米/64cm3 96平方厘米/96cm2
【分析】正方体棱长=棱长总和÷12,正方体体积=棱长×棱长×棱长,正方体表面积=棱长×棱长×6,据此列式计算。
【详解】48÷12=4(厘米)
4×4×4=64(立方厘米)
4×4×6=96(平方厘米)
它的体积是64立方厘米,表面积是96平方厘米。
【点睛】关键是熟悉正方体特征,掌握并灵活运用正方体表面积和体积公式。
9.1350
【分析】9米=90分米,把一根长9米的方钢截成3段,要锯2次,每次增加2个面积,一共则将了(2×2)个面积,已知表面积增加了60平方分米,用60÷4即可求出增加的每个面积;再根据长方体的体积=横截面积×长,用60÷4×90即可求出方钢的体积。
【详解】9米=90分米
2×(3-1)
=2×2
=4(个)
60÷4×90
=15×90
=1350(立方分米)
原来方钢的体积是1350立方分米。
【点睛】本题主要考查了立体图形的切割,关键是明确表面积增加了哪些面。
10.96
【分析】由题意可知,从长方体中截去一个最大正方体,则这个正方体的棱长是4cm,剩下的体积等于长方体的体积减去正方体的体积,根据长方体的体积公式:V=abh,正方体的体积公式:V=a3,据此进行计算即可。
【详解】8×5×4-4×4×4
=160-64
=96(cm3)
则剩下的体积是96。
【点睛】本题考查长方体和正方体的体积,熟记公式是解题的关键。
11.54
【分析】根据题意,一个长方体切成两个同样的正方体,那么表面积增加了2个正方形截面的面积,用增加的表面积除以2,求出一个正方形截面的面积,再根据正方形的面积公式确定正方体的棱长;
根据正方体的体积公式V=a3,求出一个正方体的体积,再乘2,即是这个长方体的体积。
【详解】18÷2=9(cm2)
9=3×3,所以正方体的棱长是3cm;
一个正方体的体积:3×3×3=27(cm3)
长方体的体积:27×2=54(cm3)
这个长方体的体积是54cm3。
【点睛】掌握长方体切割的特点,明确表面积增加的是哪些面的面积,以此为突破口,求出一个截面的面积,再利用正方体或长方体体积公式解答。
12.9
【分析】根据观察物体的方法,这个立体图形从前面看有,有3个小正方形,从右面看,有3个小正方形,从上面看,有3个小正方形,共有(3+3+3)个面露在外面,用正方形的面积公式,即可求出露在外面的面积是多少。
【详解】3+3+3=9(个)
10×10×9=900(平方分米)=9(平方米)
即露在外面的面积是9平方米。
【点睛】此题主要考查组合图形的表面积的求法,通过观察几何体,利用正方形的面积公式即可解决问题。
13.√
【分析】把一根长方体木料锯成3段,增加4个截面的面积,以长方体的最小面为截面时,表面积增加的最少,以长方体的最大面为截面时,表面积增加的最多,据此解答。
【详解】2×(3-1)
=2×2
=4(个)
4米=40分米,0.5米=5分米。
情况1:40×5×4
=200×4
=800(平方分米)
情况2:40×6×4
=240×4
=960(平方分米)
情况3:5×6×4
=30×4
=120(平方分米)
因为120平方分米<800平方分米<960平方分米,所以表面积最少增加120平方分米。
故答案为:√
【点睛】本题主要考查立体图形的切拼,明确增加截面的数量和每个截面的面积是解答题目的关键。
14.×
【分析】由长方体的体积公式可知,长方体的体积=底面积×高,长方体的体积与它的底面积和高有关,当长方体的高相等时,长方体的底面积越大,长方体的体积就越大,据此解答。
【详解】分析可知,长方体的高不变,长方体的底面积越大,它的体积就越大,所以原题说法错误。
故答案为:×
【点睛】熟练掌握长方体的体积计算公式是解答题目的关键。
15.×
【分析】正方体六个面的面积之和叫作它的表面积,正方体的表面积=棱长×棱长×6;正方体所占空间的大小叫作它的体积,正方体的体积=棱长×棱长×棱长,表面积和体积的计量单位不相同,二者不能比较大小,据此解答。
【详解】6×6×6
=36×6
=216(平方厘米)
6×6×6
=36×6
=216(立方厘米)
所以,正方体的表面积是216平方厘米,正方体的体积是216立方厘米,表面积和体积不能比较大小。
故答案为:×
【点睛】掌握正方体的表面积和体积计算公式,明确不是同类量不能比较大小是解答题目的关键。
16.×
【分析】立方的算法是三个相同的数相乘,得出这个数的立方,求一个数的立方(三次方)的运算方法,可以用公式表示为a =a×a×a。据此解答。
【详解】根据分析得,a =a×a×a;比如求2的立方,计算方法是23=2×2×2=8。所以原题的说法是错误的。
故答案为:×
【点睛】此题主要通过正方体的体积一章相关的知识,从而掌握求一个数的立方的计算方法。
17.√
【分析】长方体中如有两个面是正方形,那么这两个面一定是相对的面,这两个相对的面上的8条棱长度一定相等,剩下的也就是4个长方形不在正方形面上的4条棱也相等,所以一个长方体中有四个面完全一样,那么另外两个面一定是正方形。
【详解】假如长方体中两个正方形面是左右面,那么这个长方体的宽和高的长度相等,进而可得出4个长方形面的宽都相等,又由于剩下的4条长相等,所以一个长方体中有四个面完全一样,那么另外两个面是正方形;
故答案为:√
【点睛】此题考查的长方体是一种特殊的长方体,需要记住:“有两个面是正方形的长方体,另外四个长方形的面一定完全相同”这个结论,现实生活中很多包装盒都是做成这种形状。
18.56平方分米
【分析】长方体有6个面,有三组相对的面完全相同;长方体6个面的面积就是长方体表面积;前面或后面的面积=长×高,左面或右面的面积=宽×高,上面或下面的面积=长×宽。据此解答。
【详解】8×4+6×4
=32+24
=56(平方分米)
即长方体下面、左面的面积和是56平方分米。
19.304平方厘米
【分析】这个物体的表面积等于小正方体4个面的面积加上大长方体的表面积,据此解答即可。
【详解】2×2×4+(12×4+12×6+4×6)×2
=4×4+(48+72+24)×2
=16+144×2
=16+288
=304(平方厘米)
20.2.08平方米;192升
【分析】先把4分米化为0.4米,观察题意可知,油桶的表面积由底面、前面、后面、左面和右面一共5个面的面积组成,已知底面的长和宽都是0.4米,高为1.2米,则用0.4×1.2×4+0.4×0.4即可求出油桶的表面积;再把1.2米化为12分米,根据长方体体积公式:长方体的体积=长×宽×高,用4×4×12即可求出油桶的容积。
【详解】4分米=0.4米
0.4×1.2×4+0.4×0.4
=1.92+0.16
=2.08(平方米)
1.2米=12分米
4×4×12
=16×12
=192(立方分米)
192立方分米=192升
答:至少要用2.08平方米铁皮;它最多可以装油192升。
【点睛】本题考查了长方体表面积公式和体积公式的灵活应用,注意无盖油桶只求5个面的面积,以及计算时要先统一单位。
21.39厘米
【分析】根据题意,水面上升部分的体积,就是铁块的体积,再根据长方体的体积公式,求出铁块的高。
【详解】120×120×(47-21)÷(100×96)
=14400×26÷9600
=39(厘米)
答:这个长方体铁块的高是39厘米。
【点睛】本题考查用排水法求物体的体积,明确水面上升部分的体积就是铁块的体积是解答此题的关键。
22.396立方米
【详解】22×10×1.8=396(立方米)
答:这个蓄水池最多可蓄水396立方米.
23.46.875立方分米
【详解】试题分析:由题意可知:这个长方体木料的宽和高都是:7.5÷3=2.5(分米),进而根据长方体的体积公式:V=abh,解答即可.
解:这个长方体木料的宽和高都是:7.5÷3=2.5(分米),
7.5×2.5×2.5=46.875(立方分米);
答:这根木料的体积是46.875立方分米.
点评:求出这个长方体木料的宽和高,是解答此题的关键.
24.1800立方厘米
【分析】把长方体木料截成3段后,表面积比原来增加了120平方厘米,增加的是这个长方体木料4个横截面的面积,用120除以4,即可求出长方体横截面的面积,再根据长方体的体积公式:V=Sh,进行解答即可。
【详解】120÷4×60
=30×60
=1800(立方厘米)
答:这根木料原来的体积是1800立方厘米。
【点睛】此题考查长方体的体积公式的计算应用,抓住长方体的切割特点,求出长方体的底面积是解决本题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第一单元长方体和正方体必考题检测卷(单元测试)数学六年级上册苏教版
一、选择题
1.长方体的长、宽、高都扩大到原来的3倍,则它的体积扩大到原来的( )倍。
A.3 B.9 C.18 D.27
2.下面的平面图中,( )不能折成正方体。
A. B. C.
3.用100立方米的沙子铺在一段长是40米,宽是5米的路上,可以铺( )米厚。
A.0.5 B.0.4 C.2
4.一个矿泉水瓶的容积330( )。
A.升 B.毫升 C.立方米 D.立方分米
5.( )个小正方体可以拼成一个大正方体。
A.27 B.16 C.24 D.4
6.如果正方体和长方体的底面周长相等,高也相等,那么它们的体积( )。
A.正方体大 B.长方体大 C.无法比较
二、填空题
7.1.2L=( )cm3 750dm3=( )m3
3dm28cm2=( )dm2 0.69m3=( )dm3=( )mL
8.一个棱长总和是48厘米的正方体纸箱,它的体积是( ),表面积是( )。
9.一根长9米的方钢,把它横截成3段时,表面积增加了60平方分米,原来方钢的体积是( )立方分米。
10.一个长方体的长、宽、高分别是8cm、5cm和4cm,截去一个最大正方体后,剩下的体积是( )。
11.一个长方体刚好可以切成两个同样的正方体,切开后表面积增加了18cm2,这个长方体的体积是( )cm3。
12.(如图)在墙角堆放4个棱长是10分米的正方体纸箱,露在外面的面积是( )平方米。
三、判断题
13.一根长方体木料,长4米,宽0.5米,厚6分米,把它锯成3段,表面积最少增加120平方分米。( )
14.长方体的底面积越大,它的体积就越大。( )
15.一个正方体的棱长是6厘米,它的表面积和体积相等。( )
16.(a不为0)。( )
17.如果一个长方体四个面完全一样,那么另外两个面是正方形。( )
四、图形计算
18.计算长方体下面、左面的面积和。
19.求这个物体的表面积(单位:厘米)
五、解答题
20.用铁皮做一个无盖的长方体油桶,底面是边长为4分米的正方形,高是1.2米。至少要用多少平方米铁皮?它最多可以装油多少升?
21.已知一个正方体容器,棱长是120厘米,容器内的水面高度是21厘米,现在将一个长方体铁块完全沉入水中,水面高度上升至47厘米。如果铁块的长和宽分别是100厘米和96厘米,那么这个长方体铁块的高是多少厘米?
22.某海岛战士为解决岛上淡水缺乏问题,和当地居民共同修建一个长22m,宽10m,深1.8m的淡水蓄水池,这个蓄水池最多可以蓄水多少立方米?
23.一根7.5dm长的长方体木料,把它平均锯成3段,正好分成3个完全一样的正方体,这根木料的体积是多少立方分米?
24.把一根长60厘米的长方体木料锯成3段(如图),表面积比原来增加了120平方厘米。这根木料原来的体积是多少立方厘米?
参考答案:
1.D
【分析】根据长方体的体积=长×宽×高,以及积的变化规律“一个因数不变,另一个因数乘几或除以几(0除外),积也乘(或除以)几”可知,积扩大的倍数等于因数扩大倍数的乘积。
【详解】3×3×3
=9×3
=27
则一个长方体的长、宽、高都扩大到原来的3倍,则它的体积也扩大到原来的27倍。
故答案为:D
【点睛】本题考查长方体体积公式以及积的变化规律的应用。
2.A
【分析】根据正方体展开图的类型,主要分为“1-4-l”型,“2-3-1”型, “2-2-2”型,“3-3”型,据此判断解答即可。
【详解】A.,不属于正方体展开图的类型,所以不能折成正方体;
B.,属于“1-4-l”型,所以能折成正方体;
C.,属于“1-4-l”型,所以能折成正方体。
故答案为:A
【点睛】本题考查正方体的展开图,明确正方体的展开图的特征是解题的关键。
3.A
【分析】将沙子铺在路上,沙子的体积没有变,其中路面的宽为长方体的宽,沙子的厚度为长方体的高,要铺路的长度是长方体的长,根据长方体的体积=长×宽×高,代入数据即可求出铺路的厚度。
【详解】100÷40÷5=0.5(米)
即可以铺0.5米厚。
故答案为:A
【点睛】本题考查长方体体积公式的灵活运用,学生需熟练掌握长方体的高的求法。
4.B
【分析】根据生活经验以及数据的大小,选择合适的计量单位,即可解答。
【详解】一个矿泉水瓶的容积330毫升。
故答案为:B
【点睛】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活的选择。
5.A
【分析】用棱长相等的正方体拼成一个大正方体,小正方体的个数等于每条棱长上切割出的小正方体个数的3次方;据此找出是立方数的数即可得解。
【详解】A.27=33,27个小正方体可以拼成一个大正方体。
B.16=42,16不是立方数,16个小正方体不可以拼成一个大正方体。
C.24不是立方数,24个小正方体不可以拼成一个大正方体。
D.4=22,4不是立方数,4个小正方体不可以拼成一个大正方体。
故答案为:A
【点睛】本题明确小正方体的个数等于每条棱长上切割出的小正方体个数的3次方是关键。
6.A
【分析】当正方形和长方形的周长相等时,正方形的面积大于长方形的面积,正方体和长方体的体积都可以用“底面积×高”来计算,正方体和长方体的高相等,底面积大的体积就比较大,则正方体的体积大于长方体的体积,举例说明即可。
【详解】分析可知,正方体和长方体的底面周长相等时,正方体的底面积大于长方体的底面积,它们的高也相等,则正方体的体积比长方体的体积大,假设正方体和长方体的底面周长为24厘米,高为6厘米。
正方体的体积:24÷4=6(厘米)
6×6×6
=36×6
=216(立方厘米)
长方体的体积:24÷2=12(厘米)
10+2=12(厘米)
长方体的长为10厘米,宽为2厘米。
10×2×6
=20×6
=120(立方厘米)
因为216立方厘米>120立方厘米,所以如果正方体和长方体的底面周长相等,高也相等,那么正方体的体积大于长方体的体积。
故答案为:A
【点睛】熟练掌握并灵活运用长方体和正方体的体积计算公式是解答题目的关键。
7. 1200 0.75 3.08 690 690000
【分析】1L=1000mL,1mL=1cm3,1m3=1000dm3,1dm2=100cm2,1L=1dm3,高级单位换算低级单位乘进率,低级单位换算高级单位除以进率,据此解答。
【详解】(1)1.2×1000=1200(mL)
1200mL=1200cm3
(2)750÷1000=0.75(m3)
(3)3dm28cm2=3dm2+8cm2=3dm2+(8÷100)dm2=3dm2+0.08dm2=3.08dm2
(4)0.69×1000=690(dm3)
690dm3=690L
690×1000=690000(mL)
所以,1.2L=1200cm3,750dm3=0.75m3,3dm28cm2=3.08dm2,0.69m3=690dm3=690000mL。
【点睛】本题主要考查单位换算,熟记单位之间的进率和高低级单位之间转化的方法是解答题目的关键。
8. 64立方厘米/64cm3 96平方厘米/96cm2
【分析】正方体棱长=棱长总和÷12,正方体体积=棱长×棱长×棱长,正方体表面积=棱长×棱长×6,据此列式计算。
【详解】48÷12=4(厘米)
4×4×4=64(立方厘米)
4×4×6=96(平方厘米)
它的体积是64立方厘米,表面积是96平方厘米。
【点睛】关键是熟悉正方体特征,掌握并灵活运用正方体表面积和体积公式。
9.1350
【分析】9米=90分米,把一根长9米的方钢截成3段,要锯2次,每次增加2个面积,一共则将了(2×2)个面积,已知表面积增加了60平方分米,用60÷4即可求出增加的每个面积;再根据长方体的体积=横截面积×长,用60÷4×90即可求出方钢的体积。
【详解】9米=90分米
2×(3-1)
=2×2
=4(个)
60÷4×90
=15×90
=1350(立方分米)
原来方钢的体积是1350立方分米。
【点睛】本题主要考查了立体图形的切割,关键是明确表面积增加了哪些面。
10.96
【分析】由题意可知,从长方体中截去一个最大正方体,则这个正方体的棱长是4cm,剩下的体积等于长方体的体积减去正方体的体积,根据长方体的体积公式:V=abh,正方体的体积公式:V=a3,据此进行计算即可。
【详解】8×5×4-4×4×4
=160-64
=96(cm3)
则剩下的体积是96。
【点睛】本题考查长方体和正方体的体积,熟记公式是解题的关键。
11.54
【分析】根据题意,一个长方体切成两个同样的正方体,那么表面积增加了2个正方形截面的面积,用增加的表面积除以2,求出一个正方形截面的面积,再根据正方形的面积公式确定正方体的棱长;
根据正方体的体积公式V=a3,求出一个正方体的体积,再乘2,即是这个长方体的体积。
【详解】18÷2=9(cm2)
9=3×3,所以正方体的棱长是3cm;
一个正方体的体积:3×3×3=27(cm3)
长方体的体积:27×2=54(cm3)
这个长方体的体积是54cm3。
【点睛】掌握长方体切割的特点,明确表面积增加的是哪些面的面积,以此为突破口,求出一个截面的面积,再利用正方体或长方体体积公式解答。
12.9
【分析】根据观察物体的方法,这个立体图形从前面看有,有3个小正方形,从右面看,有3个小正方形,从上面看,有3个小正方形,共有(3+3+3)个面露在外面,用正方形的面积公式,即可求出露在外面的面积是多少。
【详解】3+3+3=9(个)
10×10×9=900(平方分米)=9(平方米)
即露在外面的面积是9平方米。
【点睛】此题主要考查组合图形的表面积的求法,通过观察几何体,利用正方形的面积公式即可解决问题。
13.√
【分析】把一根长方体木料锯成3段,增加4个截面的面积,以长方体的最小面为截面时,表面积增加的最少,以长方体的最大面为截面时,表面积增加的最多,据此解答。
【详解】2×(3-1)
=2×2
=4(个)
4米=40分米,0.5米=5分米。
情况1:40×5×4
=200×4
=800(平方分米)
情况2:40×6×4
=240×4
=960(平方分米)
情况3:5×6×4
=30×4
=120(平方分米)
因为120平方分米<800平方分米<960平方分米,所以表面积最少增加120平方分米。
故答案为:√
【点睛】本题主要考查立体图形的切拼,明确增加截面的数量和每个截面的面积是解答题目的关键。
14.×
【分析】由长方体的体积公式可知,长方体的体积=底面积×高,长方体的体积与它的底面积和高有关,当长方体的高相等时,长方体的底面积越大,长方体的体积就越大,据此解答。
【详解】分析可知,长方体的高不变,长方体的底面积越大,它的体积就越大,所以原题说法错误。
故答案为:×
【点睛】熟练掌握长方体的体积计算公式是解答题目的关键。
15.×
【分析】正方体六个面的面积之和叫作它的表面积,正方体的表面积=棱长×棱长×6;正方体所占空间的大小叫作它的体积,正方体的体积=棱长×棱长×棱长,表面积和体积的计量单位不相同,二者不能比较大小,据此解答。
【详解】6×6×6
=36×6
=216(平方厘米)
6×6×6
=36×6
=216(立方厘米)
所以,正方体的表面积是216平方厘米,正方体的体积是216立方厘米,表面积和体积不能比较大小。
故答案为:×
【点睛】掌握正方体的表面积和体积计算公式,明确不是同类量不能比较大小是解答题目的关键。
16.×
【分析】立方的算法是三个相同的数相乘,得出这个数的立方,求一个数的立方(三次方)的运算方法,可以用公式表示为a =a×a×a。据此解答。
【详解】根据分析得,a =a×a×a;比如求2的立方,计算方法是23=2×2×2=8。所以原题的说法是错误的。
故答案为:×
【点睛】此题主要通过正方体的体积一章相关的知识,从而掌握求一个数的立方的计算方法。
17.√
【分析】长方体中如有两个面是正方形,那么这两个面一定是相对的面,这两个相对的面上的8条棱长度一定相等,剩下的也就是4个长方形不在正方形面上的4条棱也相等,所以一个长方体中有四个面完全一样,那么另外两个面一定是正方形。
【详解】假如长方体中两个正方形面是左右面,那么这个长方体的宽和高的长度相等,进而可得出4个长方形面的宽都相等,又由于剩下的4条长相等,所以一个长方体中有四个面完全一样,那么另外两个面是正方形;
故答案为:√
【点睛】此题考查的长方体是一种特殊的长方体,需要记住:“有两个面是正方形的长方体,另外四个长方形的面一定完全相同”这个结论,现实生活中很多包装盒都是做成这种形状。
18.56平方分米
【分析】长方体有6个面,有三组相对的面完全相同;长方体6个面的面积就是长方体表面积;前面或后面的面积=长×高,左面或右面的面积=宽×高,上面或下面的面积=长×宽。据此解答。
【详解】8×4+6×4
=32+24
=56(平方分米)
即长方体下面、左面的面积和是56平方分米。
19.304平方厘米
【分析】这个物体的表面积等于小正方体4个面的面积加上大长方体的表面积,据此解答即可。
【详解】2×2×4+(12×4+12×6+4×6)×2
=4×4+(48+72+24)×2
=16+144×2
=16+288
=304(平方厘米)
20.2.08平方米;192升
【分析】先把4分米化为0.4米,观察题意可知,油桶的表面积由底面、前面、后面、左面和右面一共5个面的面积组成,已知底面的长和宽都是0.4米,高为1.2米,则用0.4×1.2×4+0.4×0.4即可求出油桶的表面积;再把1.2米化为12分米,根据长方体体积公式:长方体的体积=长×宽×高,用4×4×12即可求出油桶的容积。
【详解】4分米=0.4米
0.4×1.2×4+0.4×0.4
=1.92+0.16
=2.08(平方米)
1.2米=12分米
4×4×12
=16×12
=192(立方分米)
192立方分米=192升
答:至少要用2.08平方米铁皮;它最多可以装油192升。
【点睛】本题考查了长方体表面积公式和体积公式的灵活应用,注意无盖油桶只求5个面的面积,以及计算时要先统一单位。
21.39厘米
【分析】根据题意,水面上升部分的体积,就是铁块的体积,再根据长方体的体积公式,求出铁块的高。
【详解】120×120×(47-21)÷(100×96)
=14400×26÷9600
=39(厘米)
答:这个长方体铁块的高是39厘米。
【点睛】本题考查用排水法求物体的体积,明确水面上升部分的体积就是铁块的体积是解答此题的关键。
22.396立方米
【详解】22×10×1.8=396(立方米)
答:这个蓄水池最多可蓄水396立方米.
23.46.875立方分米
【详解】试题分析:由题意可知:这个长方体木料的宽和高都是:7.5÷3=2.5(分米),进而根据长方体的体积公式:V=abh,解答即可.
解:这个长方体木料的宽和高都是:7.5÷3=2.5(分米),
7.5×2.5×2.5=46.875(立方分米);
答:这根木料的体积是46.875立方分米.
点评:求出这个长方体木料的宽和高,是解答此题的关键.
24.1800立方厘米
【分析】把长方体木料截成3段后,表面积比原来增加了120平方厘米,增加的是这个长方体木料4个横截面的面积,用120除以4,即可求出长方体横截面的面积,再根据长方体的体积公式:V=Sh,进行解答即可。
【详解】120÷4×60
=30×60
=1800(立方厘米)
答:这根木料原来的体积是1800立方厘米。
【点睛】此题考查长方体的体积公式的计算应用,抓住长方体的切割特点,求出长方体的底面积是解决本题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
