物理人教版(2019)选择性必修第一册1.3动量守恒定律(共15张ppt)
文档属性
| 名称 | 物理人教版(2019)选择性必修第一册1.3动量守恒定律(共15张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-09-18 15:21:16 | ||
图片预览




文档简介
(共15张PPT)
第 3 课 动量守恒定律
第一章 动量守恒定律
新人教版高中物理选择性必修一
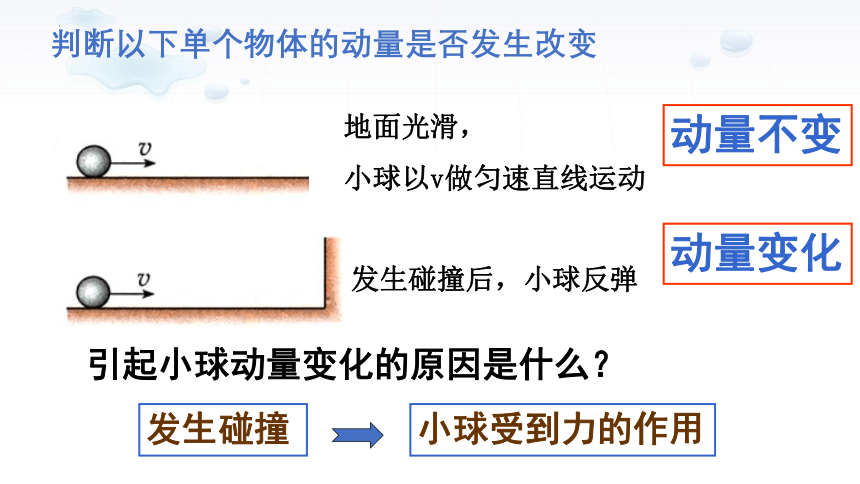
地面光滑,
小球以v做匀速直线运动
动量不变
判断以下单个物体的动量是否发生改变
发生碰撞后,小球反弹
引起小球动量变化的原因是什么?
发生碰撞
小球受到力的作用
动量变化
对于单个物体,动量不变的条件是:
物体不受外力的作用或合外力为零的时候,保持原来状态不变。
当 B 追上 A 时发生碰撞,碰撞过程中:
A 所受 B 对它的作用力是 F1
B 所受 A 对它的作用力是 F2
交流讨论 1
m1
m2
A
B
v2
v1
在光滑水平桌面上做匀速运动的两个物体沿同一直线同向运动
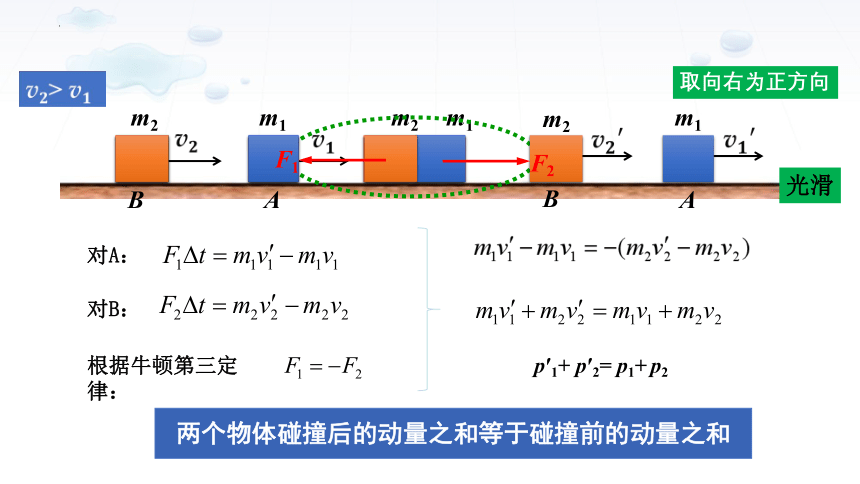
v2 > v1
作用时间 Δt 很短
碰撞后:A 的速度是 v1′ ,B 的速度是 v2′ 。
B
A
m2
m1
m2
m1
m2
m1
B
A
光滑
F2
F1
取向右为正方向
对A:
对B:
根据牛顿第三定律:
两个物体碰撞后的动量之和等于碰撞前的动量之和
p′1+ p′2= p1+ p2
A
B
m2
m1
m2
m1
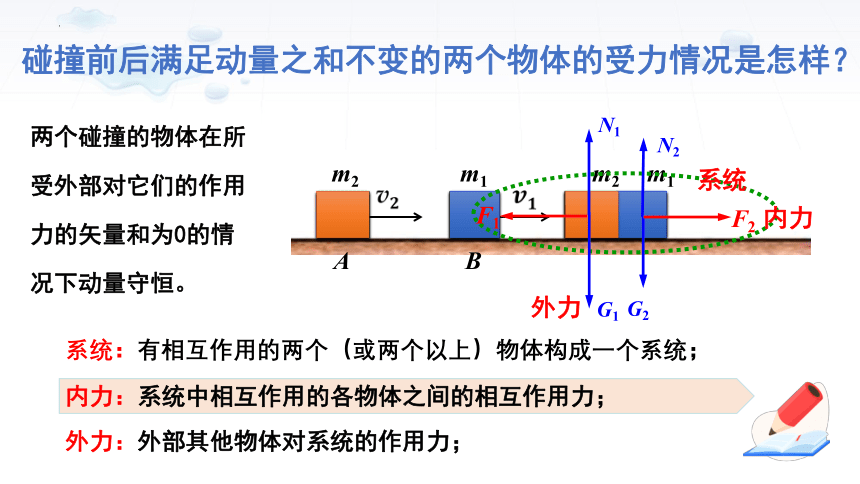
系统:有相互作用的两个(或两个以上)物体构成一个系统;
内力:系统中相互作用的各物体之间的相互作用力;
外力:外部其他物体对系统的作用力;
N1
G1
N2
G2
F1
F2
系统
内力
外力
碰撞前后满足动量之和不变的两个物体的受力情况是怎样?
两个碰撞的物体在所受外部对它们的作用力的矢量和为0的情况下动量守恒。
1.内容:如果一个系统不受外力,或者所受外力的矢量和为0,这个系统的总动量保持不变。这就是动量守恒定律。
2.表达式:
(1)p=p′或m1v1+m2v2=m1v1′+m2v2′
(系统作用前的总动量等于作用后的总动量).
(2)Δp1=-Δp2或m1Δv1=-m2Δv2
(系统内一个物体的动量变化与另一物体的动量变化等大反向)
(3)Δp=0(系统总动量的变化量为零)
二、动量守恒定律
3.适用条件
(1)系统不受外力;(理想条件)
(2)系统受到外力,但外力的合力为零;(实际条件)
在光滑水平面上有两个载有磁铁的相对运动的小车,两小车组成的系统动量守恒么?
N2
G2
N1
G1
F1
F2
两小车在运动过程中,相互排斥的磁力属于内力,整个系统的外力即重力和支持力的和为零,所以系统动量守恒。
3.适用条件
(3)系统所受外力合力不为零,但系统内力远大于外力(如碰撞、爆炸等),外力相对来说可以忽略不计,因而系统动量近似守恒;(近似条件)
宇宙大爆炸
美式桌球
③单方向的动量守恒条件:系统在某一方向上不受外力或所受合外力为零,系统在这一方向动量守恒。
小球下滑过程中,小车和小球组成的系统总动量不守恒,但在水平方向上动量守恒
【例题】在列车编组站里,一辆质量为1.8×104 kg 的货车在平直轨道上以2 m/s 的速度运动,碰上一辆质量为2.2×104 kg的静止货车,它们碰撞后结合在一起继续运动,求货车碰撞后的运动速度
①本题中相互作用的系统是什么?
②分析系统受到哪几个外力的作用?是否符合动量守恒的条件?
地面摩擦力和空气阻力
远小于内力
动量守恒
m1
m2
系统
N1
N2
F2
内力
外力
F1
G1
G2
m1
m2
【解析】以碰前货车的运动方向为正方向,设两车结合后的速度为v 。
v1 = 2 m/s ,v2 = 0
两车碰撞前的总动量为
两车碰撞后的总动量为
由动量守恒定律可得:
= 0.9 m/s
它们碰撞后结合在一起继续运动,求货车碰撞后的运动速度。
巩固提升
例2.一枚在空中飞行的火箭质量为 m,
在某时刻的速度为 v ,方向水平,燃料
即将耗尽。此时,火箭突然炸裂成两块,
其中质量为 m1的一块沿着与 v 相反的方
向飞去,速度为 v1。求炸裂后另一块的
速度 v2 。
m1,v1
m,v
v2 =
解:火箭炸裂前的总动量为
p = mv
炸裂后的总动量为
p′ = m1v1+(m-m1)v2
m1,v1
m,v
v2 =
m1v1+(m-m1)v2 = mv ,解得
外力(重力、空气阻力)远小于爆炸时的作用力,所以可以
认为系统满足动量守恒定律的条件。根据动量守恒定律可得:
交流讨论
用动量守恒定律解决问题的优越性:
2.动量守恒定律的适用范围:
只涉及初末状态,不需要分析过程中力的细节。
宏观低速、微观高速均适用。
第 3 课 动量守恒定律
第一章 动量守恒定律
新人教版高中物理选择性必修一
地面光滑,
小球以v做匀速直线运动
动量不变
判断以下单个物体的动量是否发生改变
发生碰撞后,小球反弹
引起小球动量变化的原因是什么?
发生碰撞
小球受到力的作用
动量变化
对于单个物体,动量不变的条件是:
物体不受外力的作用或合外力为零的时候,保持原来状态不变。
当 B 追上 A 时发生碰撞,碰撞过程中:
A 所受 B 对它的作用力是 F1
B 所受 A 对它的作用力是 F2
交流讨论 1
m1
m2
A
B
v2
v1
在光滑水平桌面上做匀速运动的两个物体沿同一直线同向运动
v2 > v1
作用时间 Δt 很短
碰撞后:A 的速度是 v1′ ,B 的速度是 v2′ 。
B
A
m2
m1
m2
m1
m2
m1
B
A
光滑
F2
F1
取向右为正方向
对A:
对B:
根据牛顿第三定律:
两个物体碰撞后的动量之和等于碰撞前的动量之和
p′1+ p′2= p1+ p2
A
B
m2
m1
m2
m1
系统:有相互作用的两个(或两个以上)物体构成一个系统;
内力:系统中相互作用的各物体之间的相互作用力;
外力:外部其他物体对系统的作用力;
N1
G1
N2
G2
F1
F2
系统
内力
外力
碰撞前后满足动量之和不变的两个物体的受力情况是怎样?
两个碰撞的物体在所受外部对它们的作用力的矢量和为0的情况下动量守恒。
1.内容:如果一个系统不受外力,或者所受外力的矢量和为0,这个系统的总动量保持不变。这就是动量守恒定律。
2.表达式:
(1)p=p′或m1v1+m2v2=m1v1′+m2v2′
(系统作用前的总动量等于作用后的总动量).
(2)Δp1=-Δp2或m1Δv1=-m2Δv2
(系统内一个物体的动量变化与另一物体的动量变化等大反向)
(3)Δp=0(系统总动量的变化量为零)
二、动量守恒定律
3.适用条件
(1)系统不受外力;(理想条件)
(2)系统受到外力,但外力的合力为零;(实际条件)
在光滑水平面上有两个载有磁铁的相对运动的小车,两小车组成的系统动量守恒么?
N2
G2
N1
G1
F1
F2
两小车在运动过程中,相互排斥的磁力属于内力,整个系统的外力即重力和支持力的和为零,所以系统动量守恒。
3.适用条件
(3)系统所受外力合力不为零,但系统内力远大于外力(如碰撞、爆炸等),外力相对来说可以忽略不计,因而系统动量近似守恒;(近似条件)
宇宙大爆炸
美式桌球
③单方向的动量守恒条件:系统在某一方向上不受外力或所受合外力为零,系统在这一方向动量守恒。
小球下滑过程中,小车和小球组成的系统总动量不守恒,但在水平方向上动量守恒
【例题】在列车编组站里,一辆质量为1.8×104 kg 的货车在平直轨道上以2 m/s 的速度运动,碰上一辆质量为2.2×104 kg的静止货车,它们碰撞后结合在一起继续运动,求货车碰撞后的运动速度
①本题中相互作用的系统是什么?
②分析系统受到哪几个外力的作用?是否符合动量守恒的条件?
地面摩擦力和空气阻力
远小于内力
动量守恒
m1
m2
系统
N1
N2
F2
内力
外力
F1
G1
G2
m1
m2
【解析】以碰前货车的运动方向为正方向,设两车结合后的速度为v 。
v1 = 2 m/s ,v2 = 0
两车碰撞前的总动量为
两车碰撞后的总动量为
由动量守恒定律可得:
= 0.9 m/s
它们碰撞后结合在一起继续运动,求货车碰撞后的运动速度。
巩固提升
例2.一枚在空中飞行的火箭质量为 m,
在某时刻的速度为 v ,方向水平,燃料
即将耗尽。此时,火箭突然炸裂成两块,
其中质量为 m1的一块沿着与 v 相反的方
向飞去,速度为 v1。求炸裂后另一块的
速度 v2 。
m1,v1
m,v
v2 =
解:火箭炸裂前的总动量为
p = mv
炸裂后的总动量为
p′ = m1v1+(m-m1)v2
m1,v1
m,v
v2 =
m1v1+(m-m1)v2 = mv ,解得
外力(重力、空气阻力)远小于爆炸时的作用力,所以可以
认为系统满足动量守恒定律的条件。根据动量守恒定律可得:
交流讨论
用动量守恒定律解决问题的优越性:
2.动量守恒定律的适用范围:
只涉及初末状态,不需要分析过程中力的细节。
宏观低速、微观高速均适用。
