人教版五年级下册数学8.1数学广角-找次品课件(共23张PPT)
文档属性
| 名称 | 人教版五年级下册数学8.1数学广角-找次品课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-18 06:09:26 | ||
图片预览





文档简介
(共23张PPT)
第八单元 数学广角 -- 找次品
找次品
导入新课
01
初步感知
02
自主探究
03
拓展提高
04
巩固发展
05
归纳总结
06
目
录
CONTENTS
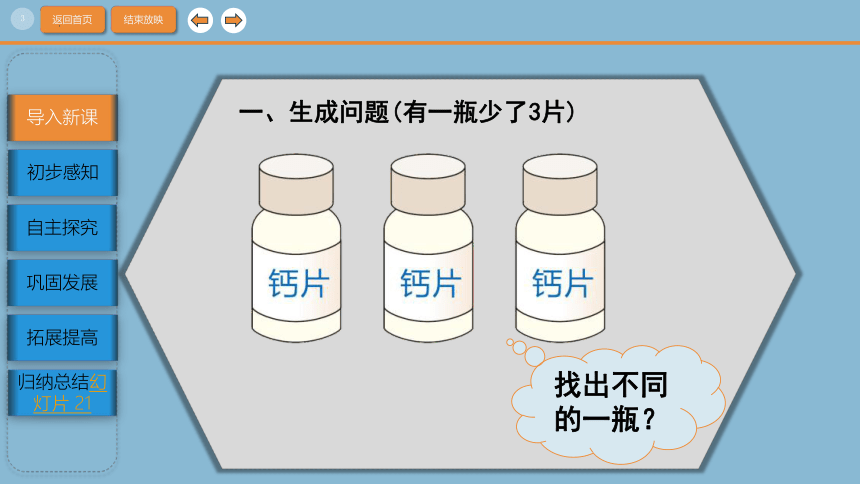
找出不同的一瓶?
一、生成问题(有一瓶少了3片)
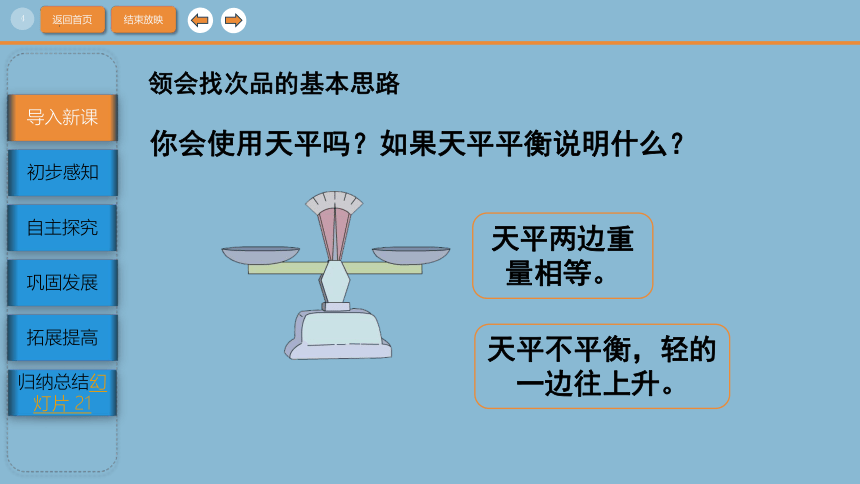
你会使用天平吗?如果天平平衡说明什么?
天平两边重量相等。
领会找次品的基本思路
天平不平衡,轻的一边往上升。
有3瓶钙片,其中1瓶少了3片,看作次品。你能设法把它找出来吗?
我用手掂了掂,掂不出来。
可以用天平称一称。
如果天平不平衡,哪瓶是次品?
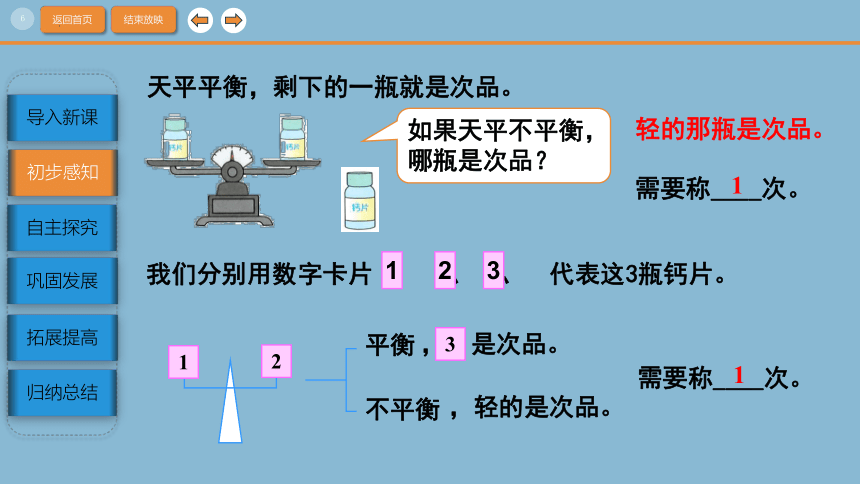
天平平衡,剩下的一瓶就是次品。
轻的那瓶是次品。
需要称____次。
1
我们分别用数字卡片 、 、 代表这3瓶钙片。
1
2
3
1
2
平衡
不平衡
, 是次品。
3
,轻的是次品。
需要称____次。
1
思考:如果5瓶钙片中有1瓶是次品(次品轻一些),用天平至少称几次能保证找到次品?
“至少称几次能保证找出次品”是指保证能找出次品的最少次数。
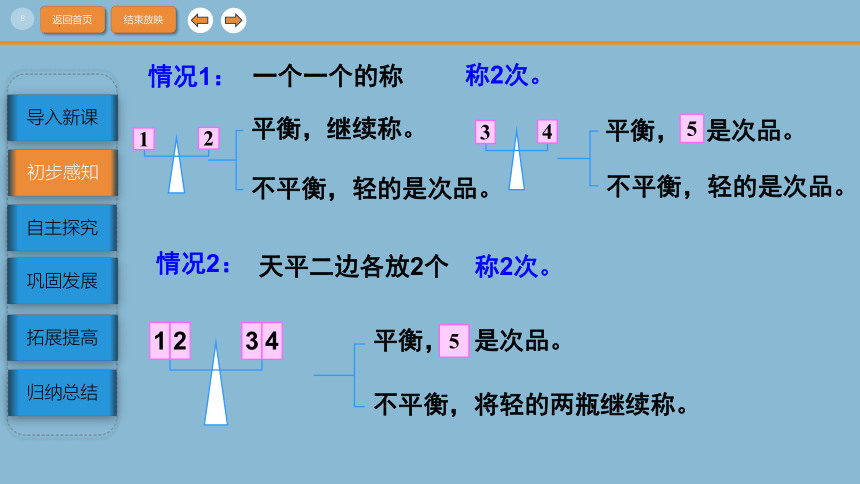
一个一个的称
1
2
平衡,继续称。
不平衡,轻的是次品。
3
4
平衡, 是次品。
不平衡,轻的是次品。
5
称2次。
情况1:
1
2
3
4
天平二边各放2个
平衡, 是次品。
不平衡,将轻的两瓶继续称。
5
称2次。
情况2:
情况1和情况2用二种方法都能只需一次就能找到次品,这种几率大不大?
遇到这种情况我们该怎么办?
我们应该做好最坏的打算
不大
当我们选用一种方法来分析和 研究问题时,应注意那可能出现的结果考虑全面,才能得出正确的结论。)
保证:找到次品
至少的次数
那些物品的个数能一次找出次品?
2个
3个呢?要怎么分?怎么称?
找出轻的一瓶?
3(1、1、1)一次
3(1、2)行吗?
天平两边数量要相等。
每个盒子里都有九个球,有一个是次品球,质量比较轻,请问如何找次品球?分组讨论把讨论的结果
写在答题卡上
记录单
分成的份数 每份的数量 至少要称的次数
5 (2,2,2,2,1) 3
9
(1,1,1,1,1,1,1,1,1)
4
3
(3,3,3)
2
3
(4,4,1)
3
将探索的结果填入下表。
请观察这几种方法,你认为那一种方法最好?
(1)观察表格、比较并展开讨论:想想为什么方法3的次数是最少的?你觉得它会和什么有关系呢?
分成 3 份的时候需要称的次数最少,只需称 2 次。
把物品平均分成3份
因为方法4第一次就排除6个正品,它排除的个数最多。
平均分成3份是最好的
如果有27个球,用咱们刚才总结出来的方法,该如何找出次品球?
27(9,9,9)
9(3,3,3)
3(1,1,1 )
81个球能至少秤几次能保证找出次品球?
27(9,9,9)
9(3,3,3)
3(1,1,1 )
81(27,27,27)
称3次
称4次
那么8个呢?物品个数和前几个数字有什么区别?
8(2,2,4)
8(3,3,2)
8(4,4,0)
把物品平均分成3份,如果不能平均分成3份,就尽量平均分成3份。也就是最多的份数与最少的份数的个数只差1个。
4(1,1,2)
2(1,1)
3(1,1,1)
4(1,1,2)
2(1,1)
称3次
称2次,最少
称3次
(3)用学到的方法解决从6、7、12、16个物体中至少几次能保证找出次品
6(2,2,2)
7(2,2,3)
2(1,1,0)
3(1,1,1)
称2次
称2次
12(4,4,4)
2(1,1,0)
4(1,1,2)
称3次
16(5,5,6)
2(1,1,0)
6(2,2,2)
称3次
用天平找次品时,所测物品数目与保证能找出次品至少需要称的次数有以下关系。(只含1个次品,已知次品比正品重或轻。)
从表中你能发现什么规律 为什么
要辨别的物品数目 保证能找出次品至少需要称的次数
2~3 1
4~9 2
10~27 3
28~81
82~243
244~729
…… ……
经过观察后,很快地分别说出了所要称的次数
辨别的物品数目2~3个(1个3),保至能找同次品至少需要称1次
4~9个(9=3ⅹ3,2个3相乘),保至能找同次品至少需要称2次
10~27个(27=3ⅹ3ⅹ3,3个3相乘),保至能找同次品至少需要称3次
28~81个(81=3ⅹ3ⅹ3ⅹ3,4个3相乘),保至能找同次品至少需要称4次
82~243个(243=3ⅹ3ⅹ3ⅹ3ⅹ3,5个3相乘),保至能找同次品至少需要称5次
……
1个次品在其中,知道次品重或轻。
3的倍数分3份,不能均分相差1。
放入天平称一称,次品立即现原形。
通过这节课的学习,你有什么收获
教材作业
第114页:第1题、第4题
练习册
配套练习册
第二十九届江西省中小学、幼儿园教师优秀教学资源展示活动(常规作品)
2023年
7月
Thank you for your attention
谢谢欣赏
谢谢欣赏
谢谢欣赏
第八单元 数学广角 -- 找次品
找次品
导入新课
01
初步感知
02
自主探究
03
拓展提高
04
巩固发展
05
归纳总结
06
目
录
CONTENTS
找出不同的一瓶?
一、生成问题(有一瓶少了3片)
你会使用天平吗?如果天平平衡说明什么?
天平两边重量相等。
领会找次品的基本思路
天平不平衡,轻的一边往上升。
有3瓶钙片,其中1瓶少了3片,看作次品。你能设法把它找出来吗?
我用手掂了掂,掂不出来。
可以用天平称一称。
如果天平不平衡,哪瓶是次品?
天平平衡,剩下的一瓶就是次品。
轻的那瓶是次品。
需要称____次。
1
我们分别用数字卡片 、 、 代表这3瓶钙片。
1
2
3
1
2
平衡
不平衡
, 是次品。
3
,轻的是次品。
需要称____次。
1
思考:如果5瓶钙片中有1瓶是次品(次品轻一些),用天平至少称几次能保证找到次品?
“至少称几次能保证找出次品”是指保证能找出次品的最少次数。
一个一个的称
1
2
平衡,继续称。
不平衡,轻的是次品。
3
4
平衡, 是次品。
不平衡,轻的是次品。
5
称2次。
情况1:
1
2
3
4
天平二边各放2个
平衡, 是次品。
不平衡,将轻的两瓶继续称。
5
称2次。
情况2:
情况1和情况2用二种方法都能只需一次就能找到次品,这种几率大不大?
遇到这种情况我们该怎么办?
我们应该做好最坏的打算
不大
当我们选用一种方法来分析和 研究问题时,应注意那可能出现的结果考虑全面,才能得出正确的结论。)
保证:找到次品
至少的次数
那些物品的个数能一次找出次品?
2个
3个呢?要怎么分?怎么称?
找出轻的一瓶?
3(1、1、1)一次
3(1、2)行吗?
天平两边数量要相等。
每个盒子里都有九个球,有一个是次品球,质量比较轻,请问如何找次品球?分组讨论把讨论的结果
写在答题卡上
记录单
分成的份数 每份的数量 至少要称的次数
5 (2,2,2,2,1) 3
9
(1,1,1,1,1,1,1,1,1)
4
3
(3,3,3)
2
3
(4,4,1)
3
将探索的结果填入下表。
请观察这几种方法,你认为那一种方法最好?
(1)观察表格、比较并展开讨论:想想为什么方法3的次数是最少的?你觉得它会和什么有关系呢?
分成 3 份的时候需要称的次数最少,只需称 2 次。
把物品平均分成3份
因为方法4第一次就排除6个正品,它排除的个数最多。
平均分成3份是最好的
如果有27个球,用咱们刚才总结出来的方法,该如何找出次品球?
27(9,9,9)
9(3,3,3)
3(1,1,1 )
81个球能至少秤几次能保证找出次品球?
27(9,9,9)
9(3,3,3)
3(1,1,1 )
81(27,27,27)
称3次
称4次
那么8个呢?物品个数和前几个数字有什么区别?
8(2,2,4)
8(3,3,2)
8(4,4,0)
把物品平均分成3份,如果不能平均分成3份,就尽量平均分成3份。也就是最多的份数与最少的份数的个数只差1个。
4(1,1,2)
2(1,1)
3(1,1,1)
4(1,1,2)
2(1,1)
称3次
称2次,最少
称3次
(3)用学到的方法解决从6、7、12、16个物体中至少几次能保证找出次品
6(2,2,2)
7(2,2,3)
2(1,1,0)
3(1,1,1)
称2次
称2次
12(4,4,4)
2(1,1,0)
4(1,1,2)
称3次
16(5,5,6)
2(1,1,0)
6(2,2,2)
称3次
用天平找次品时,所测物品数目与保证能找出次品至少需要称的次数有以下关系。(只含1个次品,已知次品比正品重或轻。)
从表中你能发现什么规律 为什么
要辨别的物品数目 保证能找出次品至少需要称的次数
2~3 1
4~9 2
10~27 3
28~81
82~243
244~729
…… ……
经过观察后,很快地分别说出了所要称的次数
辨别的物品数目2~3个(1个3),保至能找同次品至少需要称1次
4~9个(9=3ⅹ3,2个3相乘),保至能找同次品至少需要称2次
10~27个(27=3ⅹ3ⅹ3,3个3相乘),保至能找同次品至少需要称3次
28~81个(81=3ⅹ3ⅹ3ⅹ3,4个3相乘),保至能找同次品至少需要称4次
82~243个(243=3ⅹ3ⅹ3ⅹ3ⅹ3,5个3相乘),保至能找同次品至少需要称5次
……
1个次品在其中,知道次品重或轻。
3的倍数分3份,不能均分相差1。
放入天平称一称,次品立即现原形。
通过这节课的学习,你有什么收获
教材作业
第114页:第1题、第4题
练习册
配套练习册
第二十九届江西省中小学、幼儿园教师优秀教学资源展示活动(常规作品)
2023年
7月
Thank you for your attention
谢谢欣赏
谢谢欣赏
谢谢欣赏
