第一学期07月考试卷选修1-2(浙江省嘉兴市)
文档属性
| 名称 | 第一学期07月考试卷选修1-2(浙江省嘉兴市) |
|
|
| 格式 | rar | ||
| 文件大小 | 68.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-12-21 00:00:00 | ||
图片预览




文档简介
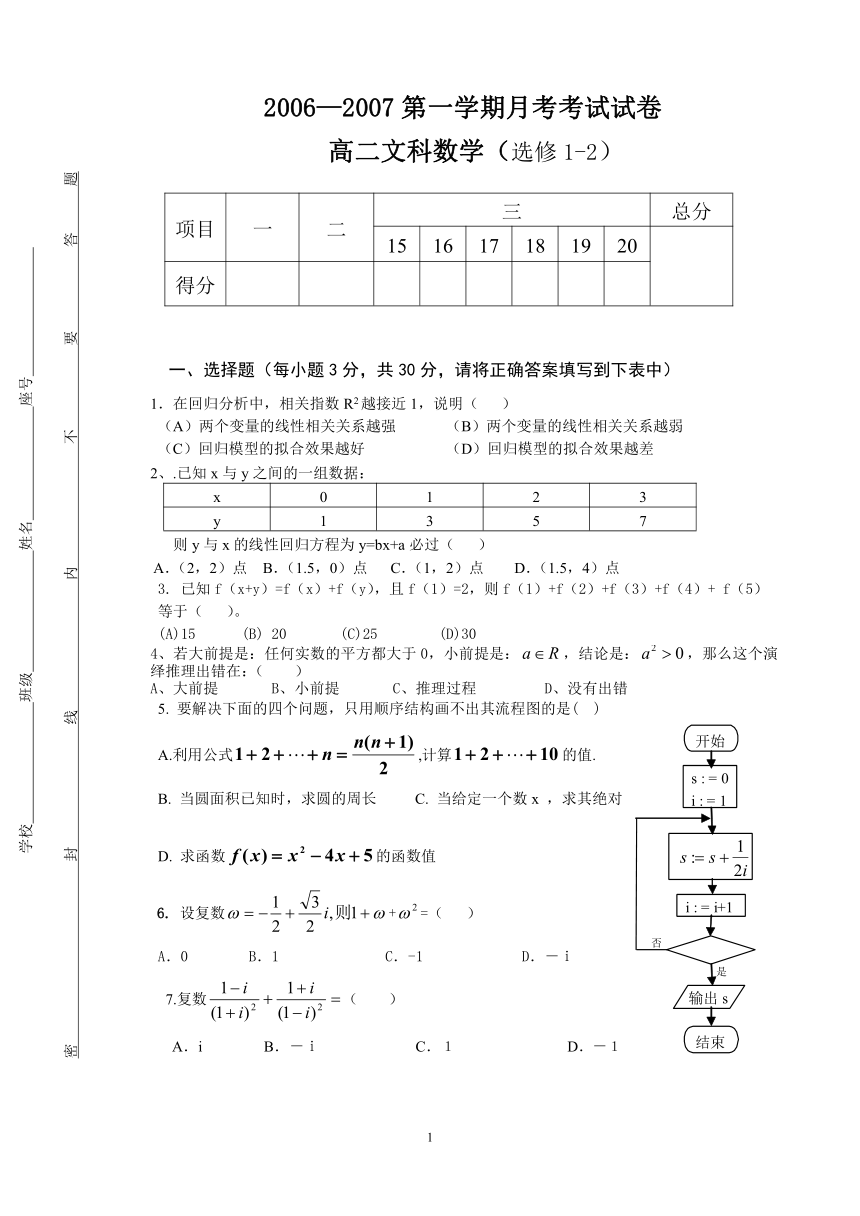
2006—2007第一学期月考考试试卷
高二文科数学(选修1-2)
项目
一
二
三
总分
15
16
17
18
19
20
得分
一、选择题(每小题3分,共30分,请将正确答案填写到下表中)
1.在回归分析中,相关指数R2越接近1,说明( )
(A)两个变量的线性相关关系越强 (B)两个变量的线性相关关系越弱
(C)回归模型的拟合效果越好 (D)回归模型的拟合效果越差
2、.已知x与y之间的一组数据:
x
0
1
2
3
y
1
3
5
7
则y与x的线性回归方程为y=bx+a必过( )
A.(2,2)点 B.(1.5,0)点 C.(1,2)点 D.(1.5,4)点
3. 已知f(x+y)=f(x)+f(y),且f(1)=2,则f(1)+f(2)+f(3)+f(4)+ f(5)
等于( )。
(A)15 (B) 20 (C)25 (D)30
4、若大前提是:任何实数的平方都大于0,小前提是:,结论是:,那么这个演绎推理出错在:( )
A、大前提 B、小前提 C、推理过程 D、没有出错
5. 要解决下面的四个问题,只用顺序结构画不出其流程图的是( )
A.利用公式,计算的值.
B. 当圆面积已知时,求圆的周长 C. 当给定一个数x ,求其绝对值
D. 求函数的函数值
6. 设复数+=( )
A.0 B.1 C.-1 D.-i
7.复数( )
A.i B.-i C.1 D.-1
8 .下面几种推理是合情推理的是( )
(1)由圆的性质类比出球的有关性质;
(2)由直角三角形、等腰三角形、等边三角形内角和是,归纳出所有三角形的内角和都是;
(3)某次考试张军成绩是100分,由此推出全班同学成绩都是100分;
(4)三角形内角和是,四边形内角和是,五边形内角和是,由此得凸多边形内角和是
A.(1)(2) B.(1)(3) C.(1)(2)(4) D.(2)(4)
9.右图给出的是计算的值的一个流程图,其中判断
框内应填入的条件是( )
(A) (B) (C) (D)
10.复数的模为( )。
A. B. C. D.
二、填空题(共6小题,每小题3分,共18分)
11.若复数对应的点在直线上,
则实数的值是
12、若有一组数据的总偏差平方和为120,相关指数为0.6,则残差平方和为
13、由“等腰三角形的两腰相等”可以类比推出正棱锥的类似属性是
14.、定义某种运算,的运算原理如右图:
则式子__________________________。
三.解答题(共6小题,共52分,写出文字说明、证明过程或演算步骤.)
15.(5分)某校学生会有如下部门:文娱部、体育部、宣传部、生活部、学习部。
请画出学生会的组织结构图。
16.(满分8分)已知复数(),试问m为何值时,
(1)为实数? (2)所对应的点落在第三象限?
17、(满分8分)在调查男女乘客是否晕机的情况中,已知男乘客晕机为28人,不会晕机的也是28人,而女乘客晕机为28人,不会晕机的为56人,(1)根据以上数据建立一个的列联表
(2)试判断是否晕机与性别有关?
常用数据表如下:
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
18.(8分)已知,,。求证中至少有一个不少于0。
19.(本小题满分10分) 已知,且复数的虚部减去它的实部所得的差等于,求复数的模;
20(满分13分)已知数列,其中是首项为1,公差为1的等差数列;是公差为的等差数列;是公差为的等差数列()。
(1)若,求;
(2)试写出关于的关系式,并求的取值范围;
(3)续写已知数列,使得是公差为的等差数列,……,
依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
高二文科数学(选修1-2)参考答案
一、选择题(每小题5分,共50分,请将正确答案填写到下表中)
题号
1
2
3
4
5
6
7
8
9
10
答案
C
D
D
A
C
D
D
C
A
D
二、填空题(共4小题,每小题5分,共20分)
11)4 12)48 13) 侧面都是全等的三角形 14) 14
15.(10分)解:学生会的组织结构图如下:
16解:(1)m为实数,z为实数,有 (2) 解:所对应的点落在第三象限,则有
6分 4分
所以当m=-3或m=5时,z为实数。7分 6分
所以当时满足题设条件。7分
17、(1)解:2×2列联表如下:
晕机
不晕机
合计
男乘客
28
28
56
女乘客
28
56
84
合计
56
84
140
…………………6分
(2)假设是否晕机与性别无关,则 的观测 值
…………………………6分
所以,我们有95%的把握认为是否晕机与性别有关,…………………………2分
18.(12分)证明:假设中没有一个不少于0,即, 4分
所以 6分
又 10分
这与假设所得结论矛盾,故假设不成立 12分
所以中至少有一个不少于0
19. (14分)解;
即
20解:解:(1). … 4分
(2), ……7分
,
当时,. …… 10分
(3)所给数列可推广为无穷数列,其中是首项为1,公差为1的等差数列,当时,数列是公差为的等差数列. …… 12分
研究的问题可以是:试写出关于的关系式,并求的取值范围. … 14分
研究的结论可以是:由,
依次类推可得
当时,的取值范围为等. … 16分
高二文科数学(选修1-2)
项目
一
二
三
总分
15
16
17
18
19
20
得分
一、选择题(每小题3分,共30分,请将正确答案填写到下表中)
1.在回归分析中,相关指数R2越接近1,说明( )
(A)两个变量的线性相关关系越强 (B)两个变量的线性相关关系越弱
(C)回归模型的拟合效果越好 (D)回归模型的拟合效果越差
2、.已知x与y之间的一组数据:
x
0
1
2
3
y
1
3
5
7
则y与x的线性回归方程为y=bx+a必过( )
A.(2,2)点 B.(1.5,0)点 C.(1,2)点 D.(1.5,4)点
3. 已知f(x+y)=f(x)+f(y),且f(1)=2,则f(1)+f(2)+f(3)+f(4)+ f(5)
等于( )。
(A)15 (B) 20 (C)25 (D)30
4、若大前提是:任何实数的平方都大于0,小前提是:,结论是:,那么这个演绎推理出错在:( )
A、大前提 B、小前提 C、推理过程 D、没有出错
5. 要解决下面的四个问题,只用顺序结构画不出其流程图的是( )
A.利用公式,计算的值.
B. 当圆面积已知时,求圆的周长 C. 当给定一个数x ,求其绝对值
D. 求函数的函数值
6. 设复数+=( )
A.0 B.1 C.-1 D.-i
7.复数( )
A.i B.-i C.1 D.-1
8 .下面几种推理是合情推理的是( )
(1)由圆的性质类比出球的有关性质;
(2)由直角三角形、等腰三角形、等边三角形内角和是,归纳出所有三角形的内角和都是;
(3)某次考试张军成绩是100分,由此推出全班同学成绩都是100分;
(4)三角形内角和是,四边形内角和是,五边形内角和是,由此得凸多边形内角和是
A.(1)(2) B.(1)(3) C.(1)(2)(4) D.(2)(4)
9.右图给出的是计算的值的一个流程图,其中判断
框内应填入的条件是( )
(A) (B) (C) (D)
10.复数的模为( )。
A. B. C. D.
二、填空题(共6小题,每小题3分,共18分)
11.若复数对应的点在直线上,
则实数的值是
12、若有一组数据的总偏差平方和为120,相关指数为0.6,则残差平方和为
13、由“等腰三角形的两腰相等”可以类比推出正棱锥的类似属性是
14.、定义某种运算,的运算原理如右图:
则式子__________________________。
三.解答题(共6小题,共52分,写出文字说明、证明过程或演算步骤.)
15.(5分)某校学生会有如下部门:文娱部、体育部、宣传部、生活部、学习部。
请画出学生会的组织结构图。
16.(满分8分)已知复数(),试问m为何值时,
(1)为实数? (2)所对应的点落在第三象限?
17、(满分8分)在调查男女乘客是否晕机的情况中,已知男乘客晕机为28人,不会晕机的也是28人,而女乘客晕机为28人,不会晕机的为56人,(1)根据以上数据建立一个的列联表
(2)试判断是否晕机与性别有关?
常用数据表如下:
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
18.(8分)已知,,。求证中至少有一个不少于0。
19.(本小题满分10分) 已知,且复数的虚部减去它的实部所得的差等于,求复数的模;
20(满分13分)已知数列,其中是首项为1,公差为1的等差数列;是公差为的等差数列;是公差为的等差数列()。
(1)若,求;
(2)试写出关于的关系式,并求的取值范围;
(3)续写已知数列,使得是公差为的等差数列,……,
依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
高二文科数学(选修1-2)参考答案
一、选择题(每小题5分,共50分,请将正确答案填写到下表中)
题号
1
2
3
4
5
6
7
8
9
10
答案
C
D
D
A
C
D
D
C
A
D
二、填空题(共4小题,每小题5分,共20分)
11)4 12)48 13) 侧面都是全等的三角形 14) 14
15.(10分)解:学生会的组织结构图如下:
16解:(1)m为实数,z为实数,有 (2) 解:所对应的点落在第三象限,则有
6分 4分
所以当m=-3或m=5时,z为实数。7分 6分
所以当时满足题设条件。7分
17、(1)解:2×2列联表如下:
晕机
不晕机
合计
男乘客
28
28
56
女乘客
28
56
84
合计
56
84
140
…………………6分
(2)假设是否晕机与性别无关,则 的观测 值
…………………………6分
所以,我们有95%的把握认为是否晕机与性别有关,…………………………2分
18.(12分)证明:假设中没有一个不少于0,即, 4分
所以 6分
又 10分
这与假设所得结论矛盾,故假设不成立 12分
所以中至少有一个不少于0
19. (14分)解;
即
20解:解:(1). … 4分
(2), ……7分
,
当时,. …… 10分
(3)所给数列可推广为无穷数列,其中是首项为1,公差为1的等差数列,当时,数列是公差为的等差数列. …… 12分
研究的问题可以是:试写出关于的关系式,并求的取值范围. … 14分
研究的结论可以是:由,
依次类推可得
当时,的取值范围为等. … 16分
