人教版数学八年级上册 11.2.1.1 三角形的内角和课件(共18张PPT)
文档属性
| 名称 | 人教版数学八年级上册 11.2.1.1 三角形的内角和课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-18 10:49:10 | ||
图片预览



文档简介
(共18张PPT)
11.2.1.1 三角形的内角和
1.掌握三角形的内角和定理,理解三角形内角和定理的证明方法.
2.掌握直角三角形的性质和判定,会运用三角形的内角和定理进行简单的计算或证明.
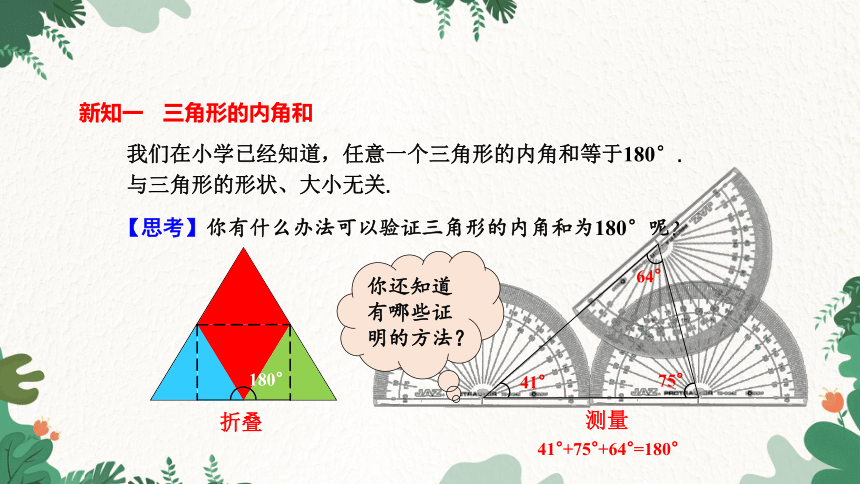
新知一 三角形的内角和
我们在小学已经知道,任意一个三角形的内角和等于180°.与三角形的形状、大小无关.
【思考】你有什么办法可以验证三角形的内角和为180°呢
你还知道有哪些证明的方法?
180°
41°
75°
64°
折叠
测量
41°+75°+64°=180°
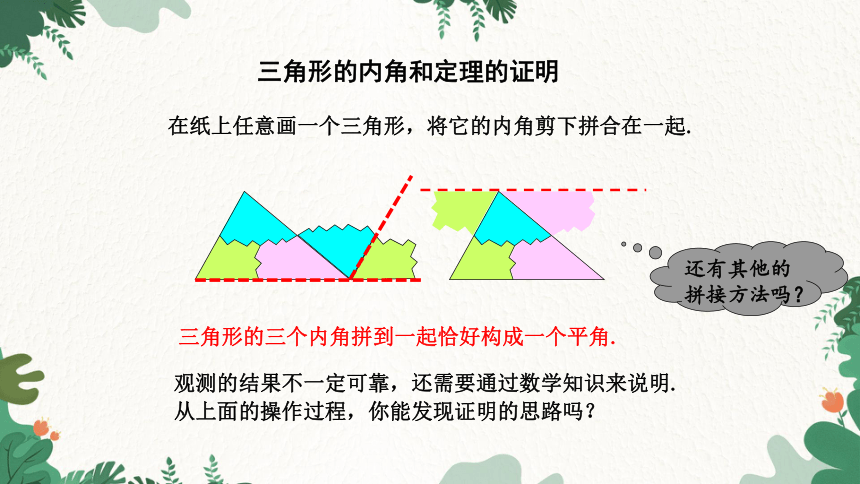
三角形的三个内角拼到一起恰好构成一个平角.
观测的结果不一定可靠,还需要通过数学知识来说明.从上面的操作过程,你能发现证明的思路吗?
三角形的内角和定理的证明
在纸上任意画一个三角形,将它的内角剪下拼合在一起.
还有其他的拼接方法吗?
D
C
B
2
1
E
A
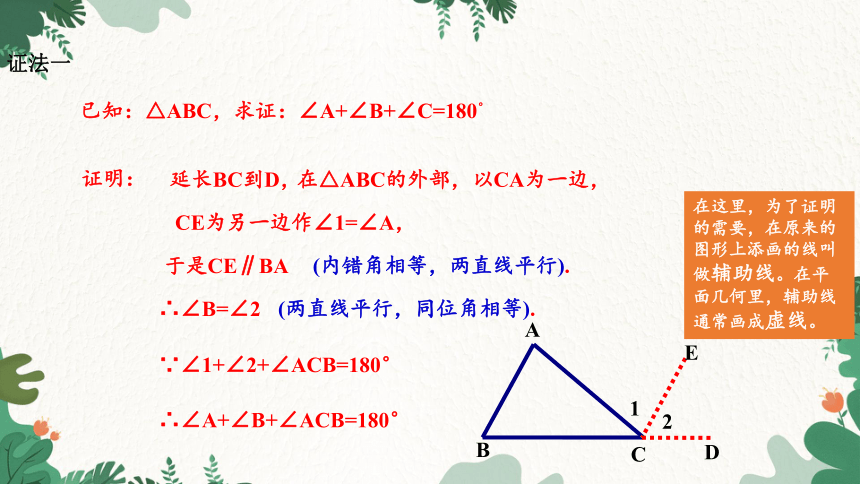
延长BC到D,
于是CE∥BA
(内错角相等,两直线平行).
∴∠B=∠2
(两直线平行,同位角相等).
∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
在△ABC的外部,以CA为一边,
CE为另一边作∠1=∠A,
已知:△ABC,求证:∠A+∠B+∠C=180°
证明:
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成虚线。
证法一
证明:
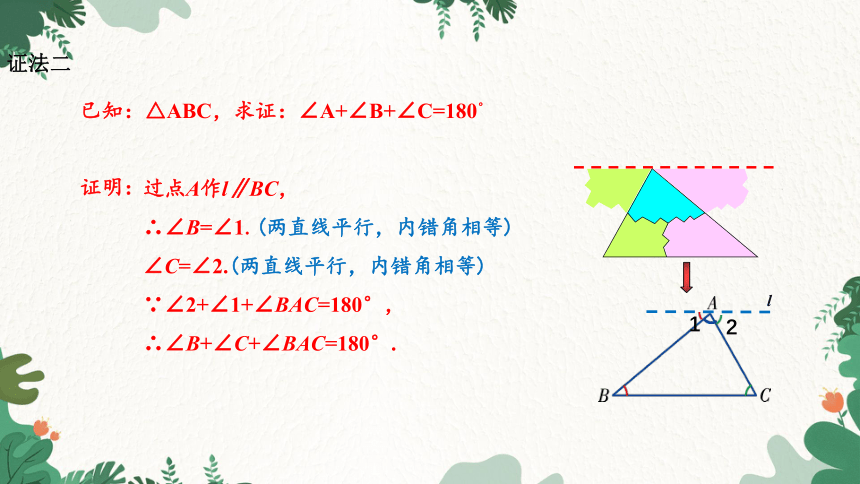
证法二
过点A作l∥BC,
∴∠B=∠1.(两直线平行,内错角相等)
∠C=∠2.(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°,
∴∠B+∠C+∠BAC=180°.
1
2
已知:△ABC,求证:∠A+∠B+∠C=180°
证法三
已知:△ABC,求证:∠A+∠B+∠C=180°
C
B
A
E
D
F
证明:过D作DE∥AC,作DF∥AB.
∴ ∠C=∠EDB,∠B=∠FDC. (两直线平行,同位角相等)
∠A+∠AED=180°,
∠AED+∠EDF=180°, (两直线平行,同旁内角相补)
∴ ∠A=∠EDF.
∵∠EDB+∠EDF+∠FDC=180°,
∴∠A+∠B+∠C=180°.
多种方法证明三角形内角和等于180°的核心是什么?
借助平行线的“移角”的功能,将三个角转化成一个平角.
1
2
C
B
A
E
D
1
2
C
B
A
E
D
F
为了证明的需要,在原来的图形上添画的线叫做辅助线.在平面几何里,辅助线通常画成虚线.
思路总结
为了证明三个角的和为180°,通过作平行线,利用平行线的性质,把所证问题转化为一个平角或同旁内角互补等,这种转化思想是数学中的常用方法.
作辅助线
例1 如图,在△ABC中, ∠BAC=40 °, ∠B=75 °, AD是△ABC的角平分线,求∠ADB的度数.
A
B
C
D
解:由∠BAC=40 °, AD是△ABC的角平分线,得
∠BAD= ∠BAC=20 °.
在△ABD中,
∠ADB=180°–∠B –∠BAD
=180°–75°–20°
=85°.
例2 已知△ABC中,∠ABC=∠C=2∠A ,BD是AC边上的高,求∠DBC的度数。
解:设∠A=x°,则∠ABC=∠C=2x°
A
B
C
D
∴x+2x+2x=180
(三角形内角和定理)
解得:x=36
∴∠C=2×36°=72°
在△BDC中,∵∠BDC=90° (三角形高的定义)
∴∠DBC=180°-90°-72°(三角形内角和定理)
∴∠DBC=18°
例3 如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛
的北偏西40°方向.求下面各题.
(1)∠DAC=_____ ,∠DAB=____,
∠EBC=_____, ∠CAB= ______ .
50°
80°
40°
30 °
(2)从C岛看A ,B两岛的视角∠C是多少度
解:∵ AD∥BE,
D
B
C
E
北
A
∴ ∠DAB+∠ABE=180°
∴ ∠ABE= 180°-∠DAB
= 180° - 80° =100°
∴ ∠ABC=∠ABE - ∠CBE
=100°- 40°=60°
在△ABC中,∠C = 180° - ∠CAB - ∠ABC
= 180°-30 °-60 °=90°
2
你能想出一个更简捷的方法来求∠C的度数吗?
解: 过点C画CF∥AD ∴ ∠1=∠DAC=50°,
∵ CF∥AD, AD ∥BE
∴ CF∥ BE
∴∠2=∠CBE =40°
∴ ∠ACB=∠1+∠2=50°+40°=90°
40°
D
C
E
北
A
F
1
50°
B
1.如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一样的玻璃,那么最省事的办法是 ( )
A.带①去 B.带②去 C.带③去 D.带①和②去
C
2. 一个三角形至少有( )
A、一个锐角 B、两个锐角
C、一个钝角 D、一个直角
B
3.如图,从A处观测C处时仰角∠CAD=30°,从B处观测C处时仰角∠CBD=45°。从C处观测A,B两处时视角∠ACB是多少?
解:在△ACD中 ∠CAD =30 °,∠D =90 °.
∴ ∠ACD =180 °-30 ° -90 °=6 0 °.
在△BCD中 ∠CBD = 45 °, ∠D =90 °.
∴ ∠BCD = 180 °-90°-45 °=45 °.
∴ ∠ACB = ∠ACD -∠BCD = 6 0 °-45 °
=15°
A
B
C
D
3.已知:如图,AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线与∠DFE的平分线相交于点P.试求∠P的度数.
解:∵AB∥CD,
∴∠BEF+∠DFE=180°.
又∠BEF的平分线与∠DFE的平分线相交于点P,
∴∠PEF= ∠BEF,∠PFE= ∠DFE,
∴∠PEF+∠PFE= (∠BEF+∠DFE)=90°.
∵∠PEF+∠PFE+∠P=180°,
∴∠P=90°.
求角度
证法
应用
转化为一个平角
或同旁内角互补
辅助线
三角形的内角和等于180 °
作平行线
转化思想
谢谢大家!
11.2.1.1 三角形的内角和
1.掌握三角形的内角和定理,理解三角形内角和定理的证明方法.
2.掌握直角三角形的性质和判定,会运用三角形的内角和定理进行简单的计算或证明.
新知一 三角形的内角和
我们在小学已经知道,任意一个三角形的内角和等于180°.与三角形的形状、大小无关.
【思考】你有什么办法可以验证三角形的内角和为180°呢
你还知道有哪些证明的方法?
180°
41°
75°
64°
折叠
测量
41°+75°+64°=180°
三角形的三个内角拼到一起恰好构成一个平角.
观测的结果不一定可靠,还需要通过数学知识来说明.从上面的操作过程,你能发现证明的思路吗?
三角形的内角和定理的证明
在纸上任意画一个三角形,将它的内角剪下拼合在一起.
还有其他的拼接方法吗?
D
C
B
2
1
E
A
延长BC到D,
于是CE∥BA
(内错角相等,两直线平行).
∴∠B=∠2
(两直线平行,同位角相等).
∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
在△ABC的外部,以CA为一边,
CE为另一边作∠1=∠A,
已知:△ABC,求证:∠A+∠B+∠C=180°
证明:
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成虚线。
证法一
证明:
证法二
过点A作l∥BC,
∴∠B=∠1.(两直线平行,内错角相等)
∠C=∠2.(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°,
∴∠B+∠C+∠BAC=180°.
1
2
已知:△ABC,求证:∠A+∠B+∠C=180°
证法三
已知:△ABC,求证:∠A+∠B+∠C=180°
C
B
A
E
D
F
证明:过D作DE∥AC,作DF∥AB.
∴ ∠C=∠EDB,∠B=∠FDC. (两直线平行,同位角相等)
∠A+∠AED=180°,
∠AED+∠EDF=180°, (两直线平行,同旁内角相补)
∴ ∠A=∠EDF.
∵∠EDB+∠EDF+∠FDC=180°,
∴∠A+∠B+∠C=180°.
多种方法证明三角形内角和等于180°的核心是什么?
借助平行线的“移角”的功能,将三个角转化成一个平角.
1
2
C
B
A
E
D
1
2
C
B
A
E
D
F
为了证明的需要,在原来的图形上添画的线叫做辅助线.在平面几何里,辅助线通常画成虚线.
思路总结
为了证明三个角的和为180°,通过作平行线,利用平行线的性质,把所证问题转化为一个平角或同旁内角互补等,这种转化思想是数学中的常用方法.
作辅助线
例1 如图,在△ABC中, ∠BAC=40 °, ∠B=75 °, AD是△ABC的角平分线,求∠ADB的度数.
A
B
C
D
解:由∠BAC=40 °, AD是△ABC的角平分线,得
∠BAD= ∠BAC=20 °.
在△ABD中,
∠ADB=180°–∠B –∠BAD
=180°–75°–20°
=85°.
例2 已知△ABC中,∠ABC=∠C=2∠A ,BD是AC边上的高,求∠DBC的度数。
解:设∠A=x°,则∠ABC=∠C=2x°
A
B
C
D
∴x+2x+2x=180
(三角形内角和定理)
解得:x=36
∴∠C=2×36°=72°
在△BDC中,∵∠BDC=90° (三角形高的定义)
∴∠DBC=180°-90°-72°(三角形内角和定理)
∴∠DBC=18°
例3 如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛
的北偏西40°方向.求下面各题.
(1)∠DAC=_____ ,∠DAB=____,
∠EBC=_____, ∠CAB= ______ .
50°
80°
40°
30 °
(2)从C岛看A ,B两岛的视角∠C是多少度
解:∵ AD∥BE,
D
B
C
E
北
A
∴ ∠DAB+∠ABE=180°
∴ ∠ABE= 180°-∠DAB
= 180° - 80° =100°
∴ ∠ABC=∠ABE - ∠CBE
=100°- 40°=60°
在△ABC中,∠C = 180° - ∠CAB - ∠ABC
= 180°-30 °-60 °=90°
2
你能想出一个更简捷的方法来求∠C的度数吗?
解: 过点C画CF∥AD ∴ ∠1=∠DAC=50°,
∵ CF∥AD, AD ∥BE
∴ CF∥ BE
∴∠2=∠CBE =40°
∴ ∠ACB=∠1+∠2=50°+40°=90°
40°
D
C
E
北
A
F
1
50°
B
1.如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一样的玻璃,那么最省事的办法是 ( )
A.带①去 B.带②去 C.带③去 D.带①和②去
C
2. 一个三角形至少有( )
A、一个锐角 B、两个锐角
C、一个钝角 D、一个直角
B
3.如图,从A处观测C处时仰角∠CAD=30°,从B处观测C处时仰角∠CBD=45°。从C处观测A,B两处时视角∠ACB是多少?
解:在△ACD中 ∠CAD =30 °,∠D =90 °.
∴ ∠ACD =180 °-30 ° -90 °=6 0 °.
在△BCD中 ∠CBD = 45 °, ∠D =90 °.
∴ ∠BCD = 180 °-90°-45 °=45 °.
∴ ∠ACB = ∠ACD -∠BCD = 6 0 °-45 °
=15°
A
B
C
D
3.已知:如图,AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线与∠DFE的平分线相交于点P.试求∠P的度数.
解:∵AB∥CD,
∴∠BEF+∠DFE=180°.
又∠BEF的平分线与∠DFE的平分线相交于点P,
∴∠PEF= ∠BEF,∠PFE= ∠DFE,
∴∠PEF+∠PFE= (∠BEF+∠DFE)=90°.
∵∠PEF+∠PFE+∠P=180°,
∴∠P=90°.
求角度
证法
应用
转化为一个平角
或同旁内角互补
辅助线
三角形的内角和等于180 °
作平行线
转化思想
谢谢大家!
