人教版数学八年级上册 11.1.2 三角形的高、中线与角平分线课件(共22张PPT)
文档属性
| 名称 | 人教版数学八年级上册 11.1.2 三角形的高、中线与角平分线课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-18 10:54:49 | ||
图片预览





文档简介
(共22张PPT)
11.1.2 三角形的高、中线与角平分线
1.掌握三角形中三条重要的线段的概念;
2.会用工具准确画出三角形的高、中线与角平分线;
3.了解三角形的三条高,三条中线,三条角平分线的定义和特征.
定义 图示
垂线
线段中点
角平分线
O
B
A
A
B
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线
把一条线段分成两条相等的线段的点
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线
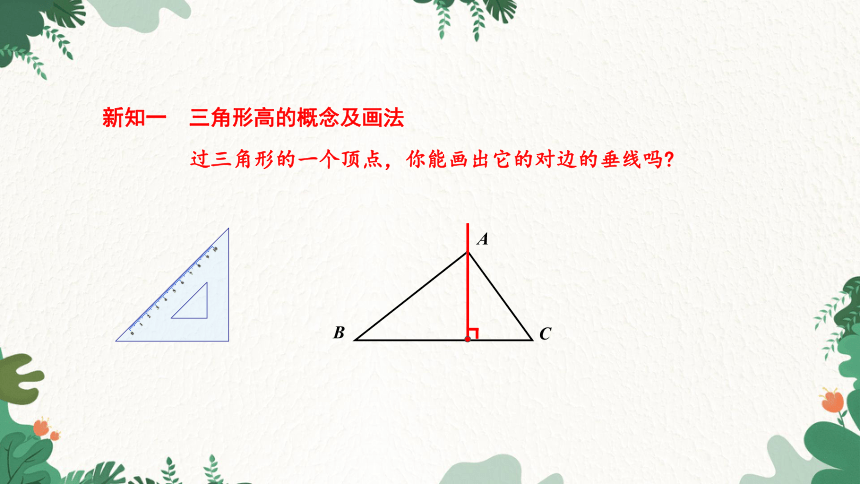
新知一 三角形高的概念及画法
过三角形的一个顶点,你能画出它的对边的垂线吗
B
A
C
0 1 2 3 4 5 6 7 8 9 10
三角形的高的定义
从三角形的一个顶点,向它的对边所在直线画垂线,顶点和垂足之间的线段叫做三角形的高。
A
B
C
D
如右图, 线段AD是BC边上的高.
几何语言:AD⊥BC于点D,读作AD垂直BC于点D或∠ADC=∠ADB=90°.
0 1 2 3 4 5 6 7 8 9 10
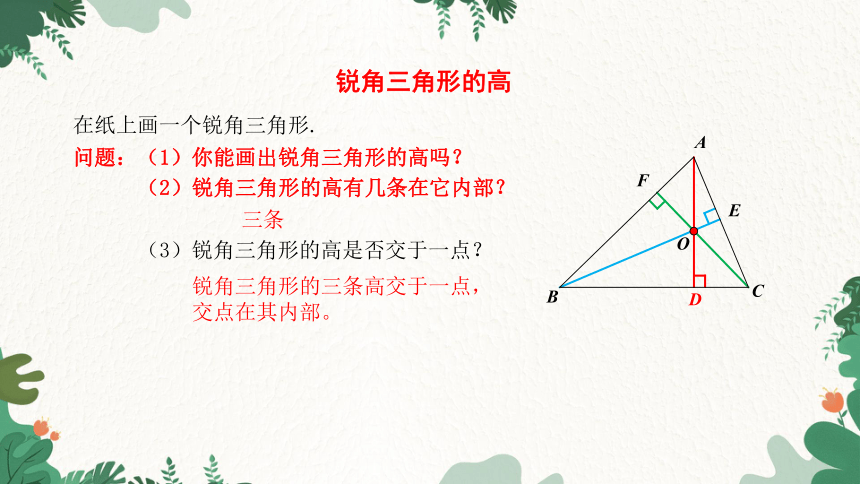
锐角三角形的高
在纸上画一个锐角三角形.
三条
(3)锐角三角形的高是否交于一点?
锐角三角形的三条高交于一点,交点在其内部。
A
B
C
E
D
F
问题:(1)你能画出锐角三角形的高吗?
(2)锐角三角形的高有几条在它内部?
O
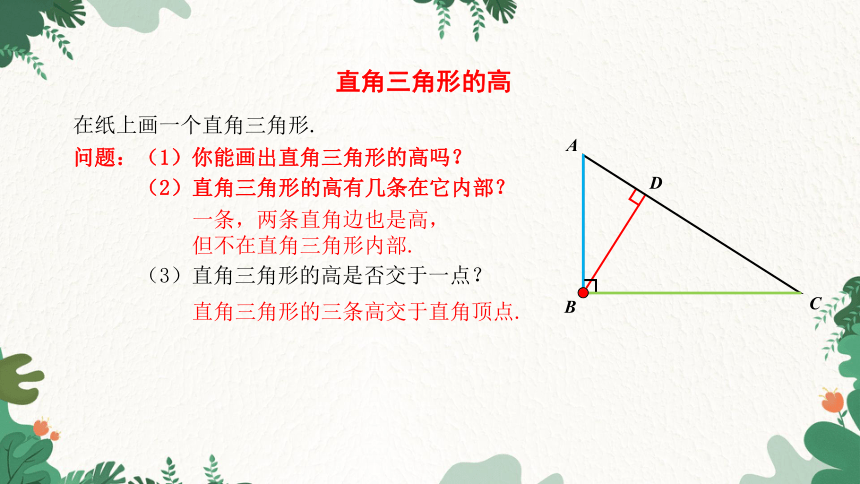
直角三角形的高
在纸上画一个直角三角形.
一条,两条直角边也是高,但不在直角三角形内部.
(3)直角三角形的高是否交于一点?
直角三角形的三条高交于直角顶点.
问题:(1)你能画出直角三角形的高吗?
(2)直角三角形的高有几条在它内部?
A
B
C
D
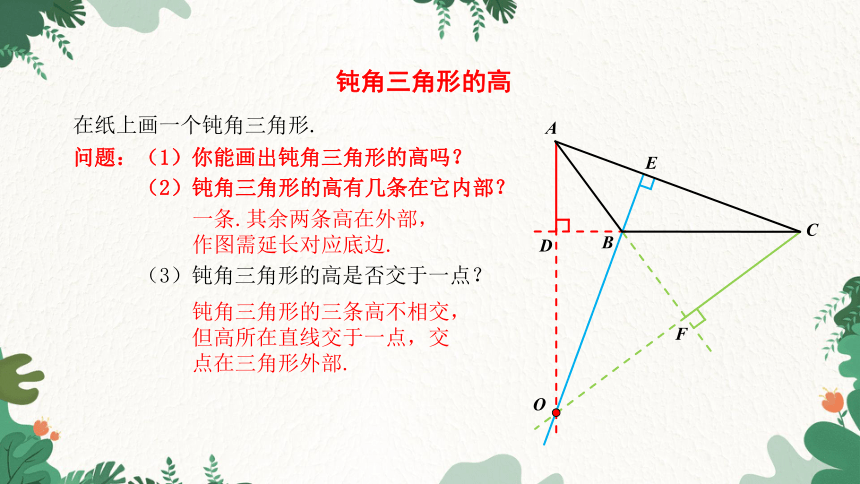
钝角三角形的高
在纸上画一个钝角三角形.
一条.其余两条高在外部,作图需延长对应底边.
(3)钝角三角形的高是否交于一点?
钝角三角形的三条高不相交,但高所在直线交于一点,交点在三角形外部.
问题:(1)你能画出钝角三角形的高吗?
(2)钝角三角形的高有几条在它内部?
D
E
F
A
B
C
O
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1
1
相交
相交
不相交
相交
相交
相交
三条高所在直线的交点的位置
三角形
内部
直角顶点
三角形
外部
新知二 三角形的中线
问题1:刚才我们学习了三角形的高,我们已经知道了三角形的面积公式,你能经过三角形的一个顶点画一条线段,将这个三角形分为面积相等的两个三角形吗?
在三角形中,连接一个顶点和它的对边中点的线段叫做三角形的中线.
(1)三角形的中线是什么线?
(2)一个三角形有几条中线?
(3)三角形的中线所分成的两个三角形面积有什么关系?
三角形的中线所分成的两个三角形的面积相等,因为等底等高的三角形面积相等.
思考:
线段
三条中线
画一个锐角三角形、直角三角形、钝角三角形,再分别画出这三个三角形的三条中线.
三角形的三条中线相交于一点,
三角形三条中线的交点叫做三角形的重心.
三角形的中线把三角形分成两个面积相等的三角形.
1.定义:在三角形中,连接一个顶点和所对边的中点的线段叫做三角形的中线.
2.三角形的重心:三角形三条中线的交点.
3.三角形的重心在各三角形中的位置:在三角形内部.
4.三角形的任何一条中线把三角形分成面积相等的两个三角形.如图:AD为中线,则S△ABD=S△ACD.
5.三角形任何一边上的中线把三角形分成的两个小三角形周长之差等于原三角形长边与短边之差.△ABD的周长–△ACD的周长=AB–AC.
例 如图所示,AD是△ABC的中线,已知△ABD的周长为25 cm,AB比AC长6 cm,则△ACD的周长为( )
A.19 cm B.22 cm C.25 cm D.31 cm
解:∵AD是BC边上的中线,
∴BD=CD,
∴△ABD和△ACD周长的差
=(AB+BD+AD)–(AC+CD+AD)
=AB –AC.
∵△ABD的周长为25 cm,AB比AC长6 cm,
∴△ACD的周长为25–6=19(cm).
A
新知三 三角形的角平分线
在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫三角形的角平分线.
1
2
A
B
C
D
“三角形的角平分线”是一条线段.
几何语言:∠1=∠2= ∠BAC
三角形的角平分线的定义
B
A
C
用量角器画最简便,用圆规也能.
在一张纸上画出一个三角形并剪下,将它的一个角对折,使其两边重合.
折痕AD即为三角形的∠A的平分线.
A
B
C
D
三角形的角平分线的画法
同:都会产生一对等角
A
C
B
O
A
B
C
D
三角形的角平分线与角的平分线有何异同
异:三角形的角平分线是一条线段 , 角的平分线是一条射线
如图,分别画出锐角、直角、钝角三角形的三条角平分线,并观察它们中线的交点有什么规律?
三角形的三条角平分线相交于三角形的内部一点,称之为三角形的内心.
1.以下说法错误的是( )
A.三角形的三条高一定在三角形内部交于一点
B.三角形的三条中线一定在三角形内部交于一点
C.三角形的三条角平分线一定在三角形内部交于一点
D.一个三角形的三条高、中线、角平分线分别交于同一个点
A
2.如图,AD是△ABC的边BC上的中线,
已知AB = 5cm,AC = 3cm.△ABD的面积为a cm2,
(1)S△ABC = ______cm2;
(2)△ABD与△ACD的周长之差为_____cm.
2a
2
3.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.锐角三角形
B
4.在下图中,若AE=ED=DC,则BE、BD分别是 的中线,
图中有没有面积相等的三角形?
△ABD 、△BCE
B
A
E
D
C
解:EF是△BED的角平分线.
理由如下:
∵AD是∠BAC的平分线,
∴∠1=∠2.
∵ DE∥AC,
∴∠5=∠2=∠1.
∵EF∥AD,
∴∠3=∠5,∠4=∠1.
∴∠3=∠4.
∴EF 是△BED 的角平分线.
5.在△ABC 中,AD 是∠A 的平分线,DE∥AC 交AB于E,EF∥AD 交BC 于F,试问EF是△BED的角平分线吗?说说你的理由.
三角形的 重要线段 概念 图形 表示法 数量及交点位置
三角形 的高线 从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段 ∵AD是△ABC的高线. ∴AD⊥BC,∠ADB=∠ADC=90°. 3条;
锐角三角形:形内;
钝角三角形:形外;
直角三角形:直角顶点
三角形 的中线 三角形中,连接一个顶点和它对边中的线段 3条,
交点叫作三角形的重心.形内
三角形的 角平分线 三角形一个内角的平分线与它的对边相交,这个角顶点与交点之间的线段 3条,形内.
谢谢大家!
11.1.2 三角形的高、中线与角平分线
1.掌握三角形中三条重要的线段的概念;
2.会用工具准确画出三角形的高、中线与角平分线;
3.了解三角形的三条高,三条中线,三条角平分线的定义和特征.
定义 图示
垂线
线段中点
角平分线
O
B
A
A
B
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线
把一条线段分成两条相等的线段的点
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线
新知一 三角形高的概念及画法
过三角形的一个顶点,你能画出它的对边的垂线吗
B
A
C
0 1 2 3 4 5 6 7 8 9 10
三角形的高的定义
从三角形的一个顶点,向它的对边所在直线画垂线,顶点和垂足之间的线段叫做三角形的高。
A
B
C
D
如右图, 线段AD是BC边上的高.
几何语言:AD⊥BC于点D,读作AD垂直BC于点D或∠ADC=∠ADB=90°.
0 1 2 3 4 5 6 7 8 9 10
锐角三角形的高
在纸上画一个锐角三角形.
三条
(3)锐角三角形的高是否交于一点?
锐角三角形的三条高交于一点,交点在其内部。
A
B
C
E
D
F
问题:(1)你能画出锐角三角形的高吗?
(2)锐角三角形的高有几条在它内部?
O
直角三角形的高
在纸上画一个直角三角形.
一条,两条直角边也是高,但不在直角三角形内部.
(3)直角三角形的高是否交于一点?
直角三角形的三条高交于直角顶点.
问题:(1)你能画出直角三角形的高吗?
(2)直角三角形的高有几条在它内部?
A
B
C
D
钝角三角形的高
在纸上画一个钝角三角形.
一条.其余两条高在外部,作图需延长对应底边.
(3)钝角三角形的高是否交于一点?
钝角三角形的三条高不相交,但高所在直线交于一点,交点在三角形外部.
问题:(1)你能画出钝角三角形的高吗?
(2)钝角三角形的高有几条在它内部?
D
E
F
A
B
C
O
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1
1
相交
相交
不相交
相交
相交
相交
三条高所在直线的交点的位置
三角形
内部
直角顶点
三角形
外部
新知二 三角形的中线
问题1:刚才我们学习了三角形的高,我们已经知道了三角形的面积公式,你能经过三角形的一个顶点画一条线段,将这个三角形分为面积相等的两个三角形吗?
在三角形中,连接一个顶点和它的对边中点的线段叫做三角形的中线.
(1)三角形的中线是什么线?
(2)一个三角形有几条中线?
(3)三角形的中线所分成的两个三角形面积有什么关系?
三角形的中线所分成的两个三角形的面积相等,因为等底等高的三角形面积相等.
思考:
线段
三条中线
画一个锐角三角形、直角三角形、钝角三角形,再分别画出这三个三角形的三条中线.
三角形的三条中线相交于一点,
三角形三条中线的交点叫做三角形的重心.
三角形的中线把三角形分成两个面积相等的三角形.
1.定义:在三角形中,连接一个顶点和所对边的中点的线段叫做三角形的中线.
2.三角形的重心:三角形三条中线的交点.
3.三角形的重心在各三角形中的位置:在三角形内部.
4.三角形的任何一条中线把三角形分成面积相等的两个三角形.如图:AD为中线,则S△ABD=S△ACD.
5.三角形任何一边上的中线把三角形分成的两个小三角形周长之差等于原三角形长边与短边之差.△ABD的周长–△ACD的周长=AB–AC.
例 如图所示,AD是△ABC的中线,已知△ABD的周长为25 cm,AB比AC长6 cm,则△ACD的周长为( )
A.19 cm B.22 cm C.25 cm D.31 cm
解:∵AD是BC边上的中线,
∴BD=CD,
∴△ABD和△ACD周长的差
=(AB+BD+AD)–(AC+CD+AD)
=AB –AC.
∵△ABD的周长为25 cm,AB比AC长6 cm,
∴△ACD的周长为25–6=19(cm).
A
新知三 三角形的角平分线
在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫三角形的角平分线.
1
2
A
B
C
D
“三角形的角平分线”是一条线段.
几何语言:∠1=∠2= ∠BAC
三角形的角平分线的定义
B
A
C
用量角器画最简便,用圆规也能.
在一张纸上画出一个三角形并剪下,将它的一个角对折,使其两边重合.
折痕AD即为三角形的∠A的平分线.
A
B
C
D
三角形的角平分线的画法
同:都会产生一对等角
A
C
B
O
A
B
C
D
三角形的角平分线与角的平分线有何异同
异:三角形的角平分线是一条线段 , 角的平分线是一条射线
如图,分别画出锐角、直角、钝角三角形的三条角平分线,并观察它们中线的交点有什么规律?
三角形的三条角平分线相交于三角形的内部一点,称之为三角形的内心.
1.以下说法错误的是( )
A.三角形的三条高一定在三角形内部交于一点
B.三角形的三条中线一定在三角形内部交于一点
C.三角形的三条角平分线一定在三角形内部交于一点
D.一个三角形的三条高、中线、角平分线分别交于同一个点
A
2.如图,AD是△ABC的边BC上的中线,
已知AB = 5cm,AC = 3cm.△ABD的面积为a cm2,
(1)S△ABC = ______cm2;
(2)△ABD与△ACD的周长之差为_____cm.
2a
2
3.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.锐角三角形
B
4.在下图中,若AE=ED=DC,则BE、BD分别是 的中线,
图中有没有面积相等的三角形?
△ABD 、△BCE
B
A
E
D
C
解:EF是△BED的角平分线.
理由如下:
∵AD是∠BAC的平分线,
∴∠1=∠2.
∵ DE∥AC,
∴∠5=∠2=∠1.
∵EF∥AD,
∴∠3=∠5,∠4=∠1.
∴∠3=∠4.
∴EF 是△BED 的角平分线.
5.在△ABC 中,AD 是∠A 的平分线,DE∥AC 交AB于E,EF∥AD 交BC 于F,试问EF是△BED的角平分线吗?说说你的理由.
三角形的 重要线段 概念 图形 表示法 数量及交点位置
三角形 的高线 从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段 ∵AD是△ABC的高线. ∴AD⊥BC,∠ADB=∠ADC=90°. 3条;
锐角三角形:形内;
钝角三角形:形外;
直角三角形:直角顶点
三角形 的中线 三角形中,连接一个顶点和它对边中的线段 3条,
交点叫作三角形的重心.形内
三角形的 角平分线 三角形一个内角的平分线与它的对边相交,这个角顶点与交点之间的线段 3条,形内.
谢谢大家!
