2023-2024学年九年级数学上册 第29章 投影与视图 复习课件 (共14张PPT)
文档属性
| 名称 | 2023-2024学年九年级数学上册 第29章 投影与视图 复习课件 (共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1019.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-18 12:14:57 | ||
图片预览



文档简介
(共14张PPT)
2023-2024学年九年级数学上册教学课件★★ 第二十九章 投影与视图
1. 如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.
(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子;
1 中心投影
解:(1)灯泡在BC与DE的交点处,即O点,作图如图所示,线段FH为小亮在灯光下形成的影子;
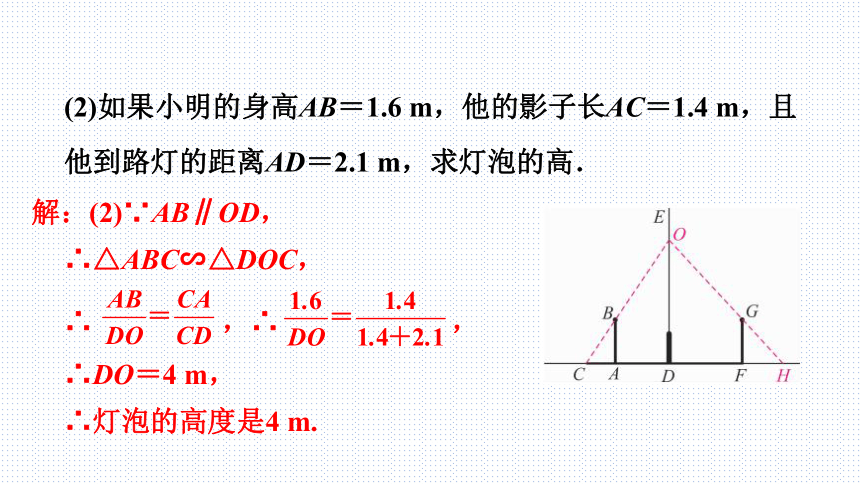
(2)如果小明的身高AB=1.6 m,他的影子长AC=1.4 m,且他到路灯的距离AD=2.1 m,求灯泡的高.
解:(2)∵AB∥OD,
∴△ABC∽△DOC,
∴DO=4 m,
∴灯泡的高度是4 m.
∴ ,∴ ,
2.如图,路灯(P点)距地面9 m,身高1.5 m的小云从距路灯的底部(O点)20 m的A点,沿OA所在的直线行走14 m到B点时,身影的长度是变长了还是变短了?变长或变短了多少 m
同理,由△NBD∽△NOP,可求得NB=1.2 m,
则小云的身影变短了4-1.2=2.8 (m),
∴变短了,短了2.8 m.
∴△MAC∽△MOP,∴ ,
即 ,解得MA=4 m,
解:如图,∵∠MAC=∠MOP=90°,∠AMC=∠OMP,
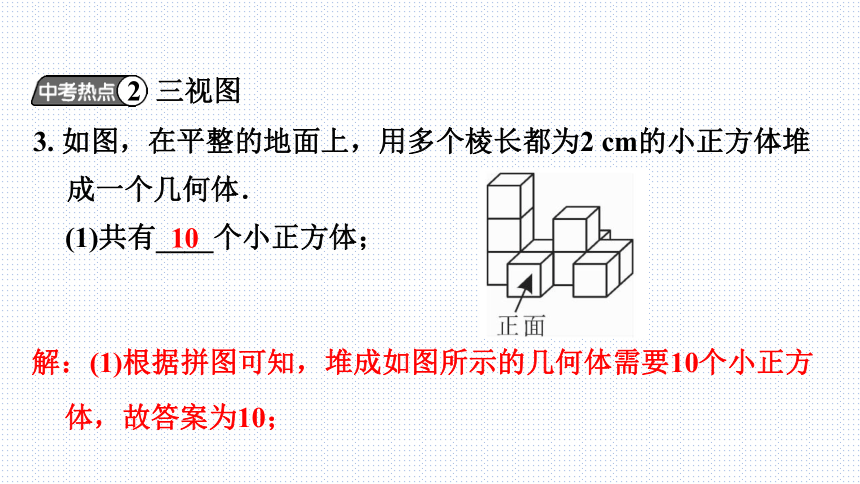
3. 如图,在平整的地面上,用多个棱长都为2 cm的小正方体堆成一个几何体.
(1)共有____个小正方体;
解:(1)根据拼图可知,堆成如图所示的几何体需要10个小正方体,故答案为10;
2 三视图
10
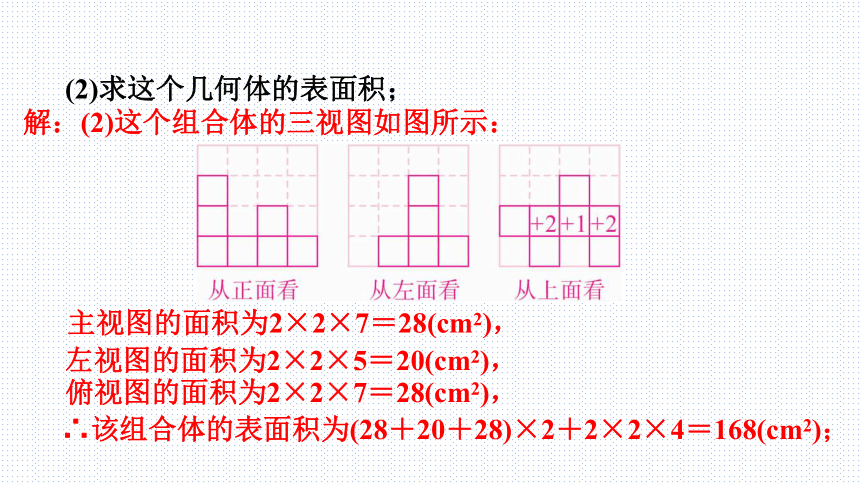
(2)求这个几何体的表面积;
解:(2)这个组合体的三视图如图所示:
主视图的面积为2×2×7=28(cm2),
左视图的面积为2×2×5=20(cm2),
俯视图的面积为2×2×7=28(cm2),
∴该组合体的表面积为(28+20+28)×2+2×2×4=168(cm2);
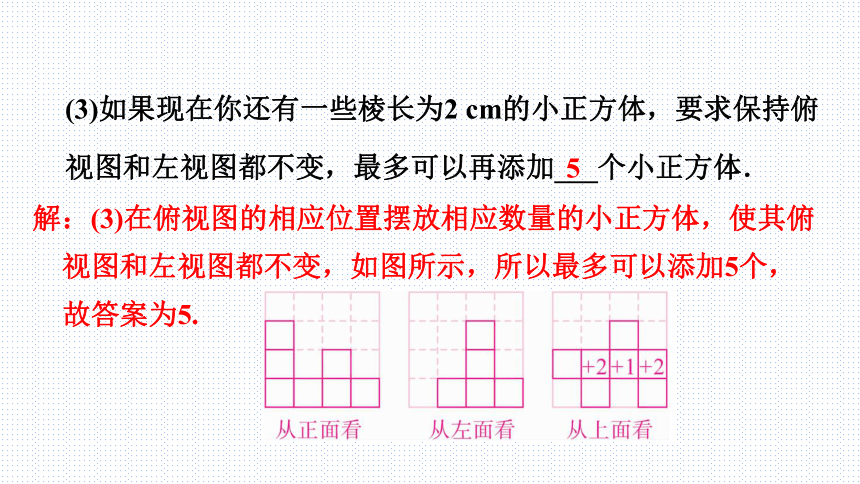
(3)如果现在你还有一些棱长为2 cm的小正方体,要求保持俯视图和左视图都不变,最多可以再添加___个小正方体.
解:(3)在俯视图的相应位置摆放相应数量的小正方体,使其俯视图和左视图都不变,如图所示,所以最多可以添加5个,故答案为5.
5
4.(2022·沙坪坝区期中)一个水壶及杯口可以近似地看成两个圆柱体叠成的图形.它从正面看和从上面看的图形如图所示.底部圆柱的高为16,直径为16,顶部圆柱的高为4,直径为8.
(1)求底部圆柱的侧面积(结果保留π);
解:(1)S侧=π×16×16=256π.
答:底部圆柱的侧面积为256π;
答:该几何体的体积为1 088π.
解:(2)V=π× ×16+π× ×4=1 024π+64π=1 088π.
(2)求该几何体的体积(结果保留π).
5.“某玩具旗舰店”根据积木数量的不同,订制了不同型号的外包装盒,所有外包装盒均为双层上盖的长方体纸箱(上盖纸板面积刚好等于底面面积的2倍,如图1),长方体纸箱的长为a厘米,宽为b厘米,高为c厘米.
(1)请用含有a,b,c的代数式表示制作
一个长方体纸箱需要___平方厘米纸板;
解:(1)制作一个长方体纸箱需要(2ac+2bc+3ab)平方厘米纸板,
故答案为(2ac+2bc+3ab);
解:(2)根据三视图知,则组成这个几何体的玩具个数最少分布情况如下图所示:
所以组成这个几何体的玩具个数最少为9个,故答案为9;
(2)如图2为若干包装好的同一型号玩具堆成几何体的三视图,则组成这个几何体的玩具个数最少为多少个?
(3)旗舰店在国庆节期间推出买一送一的活动,现要将两个同一型号的乐高积木包装在同一个大长方体的外包装盒内(如图1),已知单个乐高积木的长方体纸盒长和高相等,且宽小于长,如图3所示,现有甲,乙两种摆放方式,请分别计算甲,乙两种摆放方式所需外包装盒的纸板面积(包装盒上盖朝上),并比较哪一种方式所需纸板面积更少,说明理由.
解:(3)如图3,由题意得:a=c,a>b,
甲:2(ac+2bc+2ab)+2ab,
乙:2(2ab+2ac+bc)+2ab,
∵a>b,
∴ac>bc,∴ac-bc>0,
∵甲所需纸板面积-乙所需纸板面积
=2(ac+2bc-2ac-bc)
=2(bc-ac)<0,
∴甲种摆放方式所需外包装盒的纸板面积更少.
2023-2024学年九年级数学上册教学课件★★ 第二十九章 投影与视图
1. 如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.
(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子;
1 中心投影
解:(1)灯泡在BC与DE的交点处,即O点,作图如图所示,线段FH为小亮在灯光下形成的影子;
(2)如果小明的身高AB=1.6 m,他的影子长AC=1.4 m,且他到路灯的距离AD=2.1 m,求灯泡的高.
解:(2)∵AB∥OD,
∴△ABC∽△DOC,
∴DO=4 m,
∴灯泡的高度是4 m.
∴ ,∴ ,
2.如图,路灯(P点)距地面9 m,身高1.5 m的小云从距路灯的底部(O点)20 m的A点,沿OA所在的直线行走14 m到B点时,身影的长度是变长了还是变短了?变长或变短了多少 m
同理,由△NBD∽△NOP,可求得NB=1.2 m,
则小云的身影变短了4-1.2=2.8 (m),
∴变短了,短了2.8 m.
∴△MAC∽△MOP,∴ ,
即 ,解得MA=4 m,
解:如图,∵∠MAC=∠MOP=90°,∠AMC=∠OMP,
3. 如图,在平整的地面上,用多个棱长都为2 cm的小正方体堆成一个几何体.
(1)共有____个小正方体;
解:(1)根据拼图可知,堆成如图所示的几何体需要10个小正方体,故答案为10;
2 三视图
10
(2)求这个几何体的表面积;
解:(2)这个组合体的三视图如图所示:
主视图的面积为2×2×7=28(cm2),
左视图的面积为2×2×5=20(cm2),
俯视图的面积为2×2×7=28(cm2),
∴该组合体的表面积为(28+20+28)×2+2×2×4=168(cm2);
(3)如果现在你还有一些棱长为2 cm的小正方体,要求保持俯视图和左视图都不变,最多可以再添加___个小正方体.
解:(3)在俯视图的相应位置摆放相应数量的小正方体,使其俯视图和左视图都不变,如图所示,所以最多可以添加5个,故答案为5.
5
4.(2022·沙坪坝区期中)一个水壶及杯口可以近似地看成两个圆柱体叠成的图形.它从正面看和从上面看的图形如图所示.底部圆柱的高为16,直径为16,顶部圆柱的高为4,直径为8.
(1)求底部圆柱的侧面积(结果保留π);
解:(1)S侧=π×16×16=256π.
答:底部圆柱的侧面积为256π;
答:该几何体的体积为1 088π.
解:(2)V=π× ×16+π× ×4=1 024π+64π=1 088π.
(2)求该几何体的体积(结果保留π).
5.“某玩具旗舰店”根据积木数量的不同,订制了不同型号的外包装盒,所有外包装盒均为双层上盖的长方体纸箱(上盖纸板面积刚好等于底面面积的2倍,如图1),长方体纸箱的长为a厘米,宽为b厘米,高为c厘米.
(1)请用含有a,b,c的代数式表示制作
一个长方体纸箱需要___平方厘米纸板;
解:(1)制作一个长方体纸箱需要(2ac+2bc+3ab)平方厘米纸板,
故答案为(2ac+2bc+3ab);
解:(2)根据三视图知,则组成这个几何体的玩具个数最少分布情况如下图所示:
所以组成这个几何体的玩具个数最少为9个,故答案为9;
(2)如图2为若干包装好的同一型号玩具堆成几何体的三视图,则组成这个几何体的玩具个数最少为多少个?
(3)旗舰店在国庆节期间推出买一送一的活动,现要将两个同一型号的乐高积木包装在同一个大长方体的外包装盒内(如图1),已知单个乐高积木的长方体纸盒长和高相等,且宽小于长,如图3所示,现有甲,乙两种摆放方式,请分别计算甲,乙两种摆放方式所需外包装盒的纸板面积(包装盒上盖朝上),并比较哪一种方式所需纸板面积更少,说明理由.
解:(3)如图3,由题意得:a=c,a>b,
甲:2(ac+2bc+2ab)+2ab,
乙:2(2ab+2ac+bc)+2ab,
∵a>b,
∴ac>bc,∴ac-bc>0,
∵甲所需纸板面积-乙所需纸板面积
=2(ac+2bc-2ac-bc)
=2(bc-ac)<0,
∴甲种摆放方式所需外包装盒的纸板面积更少.
