2023-2024学年九年级数学上册.第24章 圆 复习课件(共40张PPT)
文档属性
| 名称 | 2023-2024学年九年级数学上册.第24章 圆 复习课件(共40张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-18 12:16:22 | ||
图片预览








文档简介
(共40张PPT)
2023-2024学年九年级数学上册教学课件★★第二十四章 圆
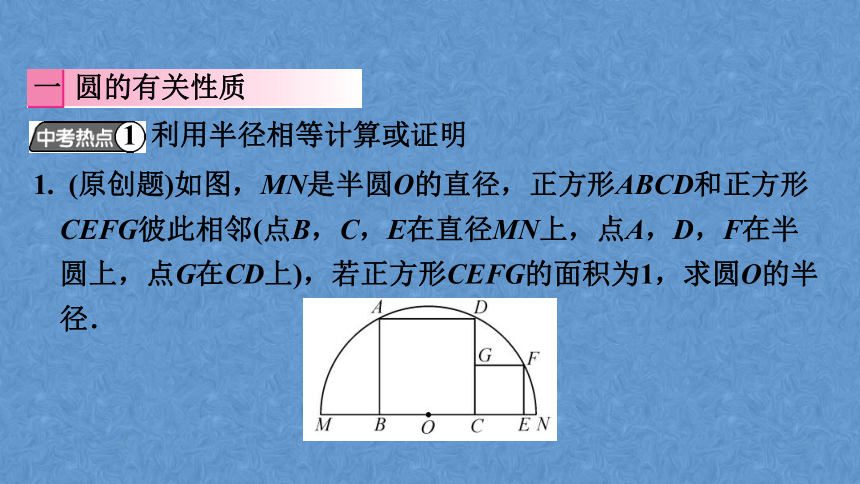
1. (原创题)如图,MN是半圆O的直径,正方形ABCD和正方形CEFG彼此相邻(点B,C,E在直径MN上,点A,D,F在半圆上,点G在CD上),若正方形CEFG的面积为1,求圆O的半径.
一 圆的有关性质
1 利用半径相等计算或证明
如图,连接OD,OF.
解:根据对称性有BO=CO,设OC=x,则CD=2x,
∴OD2=OC2+CD2=5x2,
∵正方形CEFG的面积为1,
∴CE=EF=1,
∴OF2=1+(x+1)2,
∵OD=OF,
∴1+(x+1)2=5x2,
解得x1=1,x2=- (舍去),∴OF= .
2.如图,从A地到B地有两条路可走,一条路是大半圆,另一条路是4个小半圆.有一天,一只猫和一只老鼠同时从A地到B地.老鼠见猫沿着大半圆行走,它不敢与猫同行(怕被猫吃掉),就沿着4个小半圆行走.假设猫和老鼠行走的速度相同,那么下列结论正确的是 ( )
A.猫先到达B地
B.老鼠先到达B地
C.猫和老鼠同时到达B地
D.无法确定
C
2 圆的周长与面积
3. (2022·郾城区期中)如图是一根圆形下水管道的横截面,管内有少量的污水,此时的水面宽AB为0.6米,污水的最大深度为0.1米.
(1)求此下水管横截面的半径;
3 垂径定理的应用
在Rt△OBC中,OB2=OC2+BC2,
∴OB2=(OB-0.1)2+0.09,∴BO=0.5,
即下水管横截面的半径为0.5米;
由垂径定理,得BC= AB=0.3米.
解:(1)如图1,作半径OD⊥AB于点C,连接OB,则CD=0.1米.
解:(2)如图2,过点O作OH⊥MN于点H,
(2)随着污水量的增加,水位又被抬升0.7米,求此时水面的宽度增加了多少?
∴NH=MH,
∵水位又被抬升0.7米,
∴OH=0.1+0.7-0.5=0.3米,
∴MN=0.8米,∴增加了0.2米,
∴水位又被抬升0.7米,水面的宽度增加了0.2米.
∴NH= =0.4(米),
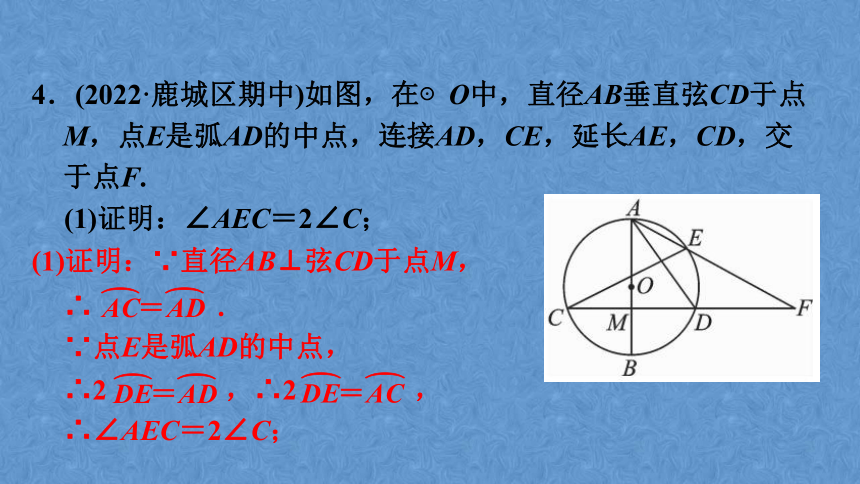
4.(2022·鹿城区期中)如图,在⊙O中,直径AB垂直弦CD于点M,点E是弧AD的中点,连接AD,CE,延长AE,CD,交于点F.
(1)证明:∠AEC=2∠C;
(1)证明:∵直径AB⊥弦CD于点M,
∵点E是弧AD的中点,
∴∠AEC=2∠C;
∴ .
∴2 ,∴2 ,
(2)当AM=4,CD=6时,求AF的长.
(2)解:∵∠AEC=2∠C,∠AEC=∠C+∠F,
∴∠C=∠F.
∵∠DAE=∠C,
∴∠DAE=∠F,∴AD=DF.
∵CD=6,直径AB⊥弦CD,
∴DF=5,∴MF=DM+DF=8,
∴DM= CD=3.
∵AM=4,∴AD= =5,
∴AF= .
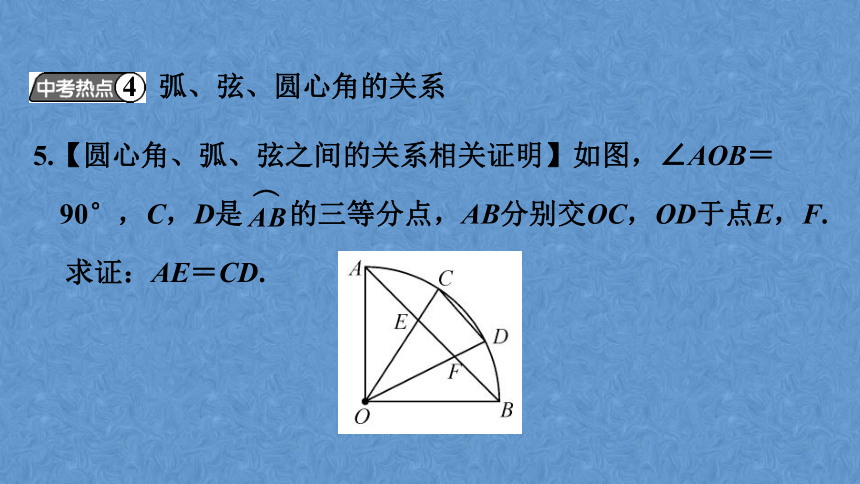
5.【圆心角、弧、弦之间的关系相关证明】如图,∠AOB=90°,C,D是 的三等分点,AB分别交OC,OD于点E,F.
求证:AE=CD.
4 弧、弦、圆心角的关系
证明:如图,连接AC,
∴∠AOC=∠COD=∠BOD=30°,AC=CD,
又∵OA=OC,
∵∠AOB=90°,OA=OB,
∴∠OAB=45°,∠AEC=∠AOC+∠OAB=75°,
∴∠ACE=∠AEC.∴AE=AC.∴AE=CD.
∵∠AOB=90°,C,D是 的三等分点,
∴ ,
∴∠ACE= ×(180°-30°)=75°.
6.【用圆心角与弧之间的关系解最值问题】如图,AB是⊙O的直径,点C是半圆上的一个三等分点,点D是 的中点,点P是直径AB上一点,若⊙O的半径为2,则PC+PD的最小值是_____.
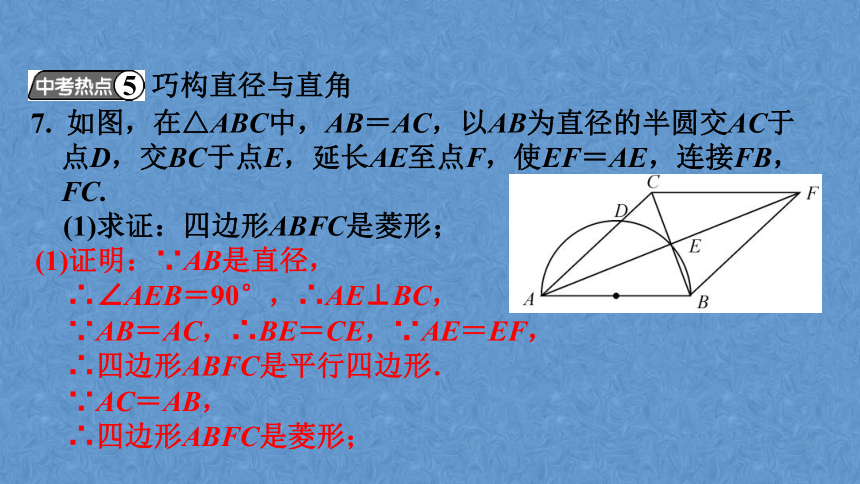
7. 如图,在△ABC中,AB=AC,以AB为直径的半圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;
(1)证明:∵AB是直径,
5 巧构直径与直角
∴∠AEB=90°,∴AE⊥BC,
∵AB=AC,∴BE=CE,∵AE=EF,
∴四边形ABFC是平行四边形.
∵AC=AB,
∴四边形ABFC是菱形;
(2)解:如图,连接BD,设CD=x,
(2)若AD=7,BE=2,求半圆形和菱形ABFC的面积.
∵AB是直径,
∴∠ADB=∠BDC=90°,
∴AB2-AD2=CB2-CD2,
∴(7+x)2-72=42-x2,
解得x=1或x=-8(舍去),
∴AC=8,BD= ,
∴S菱形ABFC=8 ,∴S半圆= ×π×42=8π.
8.(2022·朝阳区期中)如图,D是等腰三角形ABC底边的中点,过点A,B,D作⊙O.
(1)求证:AB是⊙O的直径;
∵AB=CB,AD=CD,
∴BD⊥AC,
∴∠ADB=90°,
∴AB是⊙O的直径;
(1)证明:如图,连接BD,
(2)延长CB交⊙O于点E,连接DE,求证:DC=DE;
(2)证明:∵∠E=∠A,∠C=∠A,
∴∠E=∠C,
∴DC=DE;
(3)若BC=5,CD=4,求BE长.
(3)解:∵∠E=∠A,∠C=∠C,
∴△EDC∽△ABC.
∵BC=5,CD=4,
∴ ,CA=2CD=8,
∴CE= ×8= ,
∴BE=CE-BC= -5= .
9.如图,已知⊙P的半径为2,圆心P在抛物线y= x2-1上运动,当⊙P与x轴相切时,圆心P的坐标为
____________________.
6 直线与圆的位置关系
( ,2)或(- ,2)
10. 如图,⊙O的直径BE为4,∠BAE的平分线AD交⊙O于点D,交BE于点F,C是BE延长线上一点,且FC=AC.
(1)求BD的长;
7 用“连半径,证垂直”证切线
∵BE为⊙O的直径,
∴∠BAE=90°,
∵AD平分∠BAE,∠BAD=∠EAD=45°,
∴∠BOD=2∠BAD=90°,
在Rt△BOD中,BD= ;
(1)解:如图,连接OD,
(2)求证:AC是⊙O的切线.
(2)证明:如图,连接OA.
∵AC=FC,
∴∠FAC=∠CFA,
∵∠DFO=∠CFA,
∴∠DFO=∠FAC,
∵OA=OD,
∴∠OAF=∠ODF.由(1)知∠BOD=90°,
∴∠DFO+∠ODF=∠CAF+∠OAF=90°,
∴OA⊥AC于点A,∴AC是⊙O的切线.
11. 如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D,OB与⊙O相交于点E.求证:AC是⊙O的切线.
8 用“连垂直,证半径”证切线
∵△ABC为等腰三角形,点O是底边BC的中点,
∴AO⊥BC,AO平分∠BAC,
∵AB与⊙O相切于点D,
∴OD⊥AB,而OF⊥AC,∴OF=OD,
∴AC是⊙O的切线.
证明:如图,连接OD,作OF⊥AC于点F,
12. 如图,⊙O与△ABC的AC边相切于点C,与BC边交于点E,⊙O过AB上一点D,且DE∥AO,CE是⊙O的直径.
(1)求证:AB是⊙O的切线;
9 切线长定理
∵OD=OE,
∴∠OED=∠ODE,
∵DE∥OA,
∴∠ODE=AOD,∠DEO=∠AOC,∴∠AOD=∠AOC,
∵AC是切线,∴∠ACB=90°,
∴△AOD≌△AOC(SAS),∴∠ADO=∠ACB=90°,
∵OD是半径,
∴AB是⊙O的切线;
在△AOD和△AOC中,
(1)证明:如图,连接OD,
(2)若BD=4,EC=6,求AC的长.
(2)解:∵AB是⊙O的切线,
∴∠BDO=90°,
∴BD2+OD2=OB2,∴42+32=(3+BE)2,
∴BE=2,∴BC=BE+EC=8,
∵AD,AC是⊙O的切线,
∴AD=AC,设AD=AC=x,
在Rt△ABC中,AB2=AC2+BC2,
∴(4+x)2=x2+82,解得x=6,∴AC=6.
13.如图,正方形ABCD的边长为4,⊙O的半径为1.若⊙O在正方形ABCD内平移(⊙O可以与该正方形的边相切),则点A到⊙O上的点的距离的最大值为_______.
14.【整体思想求周长】如图,PA,PB切⊙O于点A,B,PA=10,CD切⊙O于点E,交PA,PB于C,D两点,则△PCD的周长是 ( )
A.10
B.18
C.20
D.22
C
15.【三角形外接圆和内切圆综合】如图,点E是△ABC的内心,线段AE的延长线交△ABC的外接圆于点D.
(1)求证:ED=BD;
(1)证明:∵点E是△ABC的内心,
∴∠BAD=∠CAD,∠ABE=∠CBE,
∵∠CBD=∠CAD,
∴∠BAD=∠CBD,
∴∠BED=∠ABE+∠BAD,
∵∠EBD=∠CBE+∠CBD,
∴∠BED=∠EBD,
∴ED=BD;
(2)若∠BAC=90°,△ABC的外接圆⊙O的直径是6,求BD的长.
∵∠BAC=90°,
∴BC是⊙O的直径,∴∠BDC=90°,
∵⊙O的直径是6,
∴BC=6,
∵E为△ABC的内切圆的圆心,
∴∠BAD=∠CAD,∴BD=DC,
∴BD=DC= BC=3 .
(2)解:如图,连接CD,
10 正多边形与圆的相关计算和证明
16. 如图,正△ABC外切于⊙O,正方形DEFG内接于⊙O,若正△ABC的边长为6,则正方形DEFG的边长为_____.
17.如图,在边长为8的菱形ABCD中,∠DAB=60°,以点D为圆心,菱形的高DF为半径画弧,交AD于点E,交CD于点G,则图中阴影部分的面积是 ( )
A.18-3π
B.18- π
C.32 -16π
D.18 -9π
C
18.【利用圆锥公式进行相关计算】如图,在矩形纸片ABCD中,AD=6 cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的底面和侧面,则AB的长为 ( )
A.3.5 cm
B.4 cm
C.4.5 cm
D.5 cm
B
11 圆锥的侧面积与全面积
19.【分类讨论思想——旋转几何体】已知在Rt△ABC中,∠ACB=90°,AC=4,BC=3,以AB边所在的直线为轴,将△ABC旋转一周,则所得几何体的表面积为_______.
20.(2022·江阴月考)如图,AB是⊙O的直径,点C在⊙O上,BD平分∠ABC交⊙O于点D,过点D作DE⊥BC于点E.
(1)求证:DE与⊙O相切;
(1)证明:如图,连接OD.
∵OD=OB,
∴∠ODB=∠OBD.
∵BD平分∠ABC,
∴∠OBD=∠CBD,
∴∠ODB=∠CBD,
∴OD∥BE.
∵BE⊥DE,
∴OD⊥DE.
∵OD是⊙O的半径,
∴DE与⊙O相切;
(2)解:如图,过点D作DH⊥AB于点H.
(2)若AB=10,AD=6,求DE的长;
∵BD平分∠ABC,DE⊥BE,DH⊥AB,
∴DH=DE.
∵AB是⊙O的直径,∴∠ADB=90°.
∵AB=10,AD=6,
∴BD= =8.
∵ AB·DH= AD·DB,
∴DH= ,∴DE=DH= ;
(3)在(2)的条件下,直接写出CD的长为____.
6
(3)解:∵BD平分∠ABC,
∴CD=AD=6.
故答案为6.
∴ ,
21. 如图,四边形ABCD是⊙O的内接四边形,AC为直径, ,DE⊥BC,垂足为E.
(1)求证:CD平分∠ACE;
12 圆综合
∴∠BAD=∠ACD.
∵∠DCE=∠BAD,
∴∠ACD=∠DCE,
即CD平分∠ACE;
(1)证明:∵ ,
(2)解:直线ED与⊙O相切,理由如下:如图,连接OD,
(2)判断直线ED与⊙O的位置关系,并说明理由;
∵OC=OD,
∴∠OCD=∠ODC,
而∠OCD=∠DCE,
∴∠DCE=∠ODC,
∴OD∥BC,
∵DE⊥BC,
∴OD⊥DE,
∴DE为⊙O的切线;
(3)若CE=1,AC=4,求阴影部分的面积.
(3)解:如图,作OH⊥BC于点H,则四边形ODEH为矩形,
∴OD=EH,
∵CE=1,AC=4,
∴OC=OD=2,
∴CH=HE-CE=2-1=1,
在Rt△OHC中,∠HOC=30°,∠COD=60°,
∴阴影部分的面积=S扇形OCD-S△OCD
= .
2023-2024学年九年级数学上册教学课件★★第二十四章 圆
1. (原创题)如图,MN是半圆O的直径,正方形ABCD和正方形CEFG彼此相邻(点B,C,E在直径MN上,点A,D,F在半圆上,点G在CD上),若正方形CEFG的面积为1,求圆O的半径.
一 圆的有关性质
1 利用半径相等计算或证明
如图,连接OD,OF.
解:根据对称性有BO=CO,设OC=x,则CD=2x,
∴OD2=OC2+CD2=5x2,
∵正方形CEFG的面积为1,
∴CE=EF=1,
∴OF2=1+(x+1)2,
∵OD=OF,
∴1+(x+1)2=5x2,
解得x1=1,x2=- (舍去),∴OF= .
2.如图,从A地到B地有两条路可走,一条路是大半圆,另一条路是4个小半圆.有一天,一只猫和一只老鼠同时从A地到B地.老鼠见猫沿着大半圆行走,它不敢与猫同行(怕被猫吃掉),就沿着4个小半圆行走.假设猫和老鼠行走的速度相同,那么下列结论正确的是 ( )
A.猫先到达B地
B.老鼠先到达B地
C.猫和老鼠同时到达B地
D.无法确定
C
2 圆的周长与面积
3. (2022·郾城区期中)如图是一根圆形下水管道的横截面,管内有少量的污水,此时的水面宽AB为0.6米,污水的最大深度为0.1米.
(1)求此下水管横截面的半径;
3 垂径定理的应用
在Rt△OBC中,OB2=OC2+BC2,
∴OB2=(OB-0.1)2+0.09,∴BO=0.5,
即下水管横截面的半径为0.5米;
由垂径定理,得BC= AB=0.3米.
解:(1)如图1,作半径OD⊥AB于点C,连接OB,则CD=0.1米.
解:(2)如图2,过点O作OH⊥MN于点H,
(2)随着污水量的增加,水位又被抬升0.7米,求此时水面的宽度增加了多少?
∴NH=MH,
∵水位又被抬升0.7米,
∴OH=0.1+0.7-0.5=0.3米,
∴MN=0.8米,∴增加了0.2米,
∴水位又被抬升0.7米,水面的宽度增加了0.2米.
∴NH= =0.4(米),
4.(2022·鹿城区期中)如图,在⊙O中,直径AB垂直弦CD于点M,点E是弧AD的中点,连接AD,CE,延长AE,CD,交于点F.
(1)证明:∠AEC=2∠C;
(1)证明:∵直径AB⊥弦CD于点M,
∵点E是弧AD的中点,
∴∠AEC=2∠C;
∴ .
∴2 ,∴2 ,
(2)当AM=4,CD=6时,求AF的长.
(2)解:∵∠AEC=2∠C,∠AEC=∠C+∠F,
∴∠C=∠F.
∵∠DAE=∠C,
∴∠DAE=∠F,∴AD=DF.
∵CD=6,直径AB⊥弦CD,
∴DF=5,∴MF=DM+DF=8,
∴DM= CD=3.
∵AM=4,∴AD= =5,
∴AF= .
5.【圆心角、弧、弦之间的关系相关证明】如图,∠AOB=90°,C,D是 的三等分点,AB分别交OC,OD于点E,F.
求证:AE=CD.
4 弧、弦、圆心角的关系
证明:如图,连接AC,
∴∠AOC=∠COD=∠BOD=30°,AC=CD,
又∵OA=OC,
∵∠AOB=90°,OA=OB,
∴∠OAB=45°,∠AEC=∠AOC+∠OAB=75°,
∴∠ACE=∠AEC.∴AE=AC.∴AE=CD.
∵∠AOB=90°,C,D是 的三等分点,
∴ ,
∴∠ACE= ×(180°-30°)=75°.
6.【用圆心角与弧之间的关系解最值问题】如图,AB是⊙O的直径,点C是半圆上的一个三等分点,点D是 的中点,点P是直径AB上一点,若⊙O的半径为2,则PC+PD的最小值是_____.
7. 如图,在△ABC中,AB=AC,以AB为直径的半圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;
(1)证明:∵AB是直径,
5 巧构直径与直角
∴∠AEB=90°,∴AE⊥BC,
∵AB=AC,∴BE=CE,∵AE=EF,
∴四边形ABFC是平行四边形.
∵AC=AB,
∴四边形ABFC是菱形;
(2)解:如图,连接BD,设CD=x,
(2)若AD=7,BE=2,求半圆形和菱形ABFC的面积.
∵AB是直径,
∴∠ADB=∠BDC=90°,
∴AB2-AD2=CB2-CD2,
∴(7+x)2-72=42-x2,
解得x=1或x=-8(舍去),
∴AC=8,BD= ,
∴S菱形ABFC=8 ,∴S半圆= ×π×42=8π.
8.(2022·朝阳区期中)如图,D是等腰三角形ABC底边的中点,过点A,B,D作⊙O.
(1)求证:AB是⊙O的直径;
∵AB=CB,AD=CD,
∴BD⊥AC,
∴∠ADB=90°,
∴AB是⊙O的直径;
(1)证明:如图,连接BD,
(2)延长CB交⊙O于点E,连接DE,求证:DC=DE;
(2)证明:∵∠E=∠A,∠C=∠A,
∴∠E=∠C,
∴DC=DE;
(3)若BC=5,CD=4,求BE长.
(3)解:∵∠E=∠A,∠C=∠C,
∴△EDC∽△ABC.
∵BC=5,CD=4,
∴ ,CA=2CD=8,
∴CE= ×8= ,
∴BE=CE-BC= -5= .
9.如图,已知⊙P的半径为2,圆心P在抛物线y= x2-1上运动,当⊙P与x轴相切时,圆心P的坐标为
____________________.
6 直线与圆的位置关系
( ,2)或(- ,2)
10. 如图,⊙O的直径BE为4,∠BAE的平分线AD交⊙O于点D,交BE于点F,C是BE延长线上一点,且FC=AC.
(1)求BD的长;
7 用“连半径,证垂直”证切线
∵BE为⊙O的直径,
∴∠BAE=90°,
∵AD平分∠BAE,∠BAD=∠EAD=45°,
∴∠BOD=2∠BAD=90°,
在Rt△BOD中,BD= ;
(1)解:如图,连接OD,
(2)求证:AC是⊙O的切线.
(2)证明:如图,连接OA.
∵AC=FC,
∴∠FAC=∠CFA,
∵∠DFO=∠CFA,
∴∠DFO=∠FAC,
∵OA=OD,
∴∠OAF=∠ODF.由(1)知∠BOD=90°,
∴∠DFO+∠ODF=∠CAF+∠OAF=90°,
∴OA⊥AC于点A,∴AC是⊙O的切线.
11. 如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D,OB与⊙O相交于点E.求证:AC是⊙O的切线.
8 用“连垂直,证半径”证切线
∵△ABC为等腰三角形,点O是底边BC的中点,
∴AO⊥BC,AO平分∠BAC,
∵AB与⊙O相切于点D,
∴OD⊥AB,而OF⊥AC,∴OF=OD,
∴AC是⊙O的切线.
证明:如图,连接OD,作OF⊥AC于点F,
12. 如图,⊙O与△ABC的AC边相切于点C,与BC边交于点E,⊙O过AB上一点D,且DE∥AO,CE是⊙O的直径.
(1)求证:AB是⊙O的切线;
9 切线长定理
∵OD=OE,
∴∠OED=∠ODE,
∵DE∥OA,
∴∠ODE=AOD,∠DEO=∠AOC,∴∠AOD=∠AOC,
∵AC是切线,∴∠ACB=90°,
∴△AOD≌△AOC(SAS),∴∠ADO=∠ACB=90°,
∵OD是半径,
∴AB是⊙O的切线;
在△AOD和△AOC中,
(1)证明:如图,连接OD,
(2)若BD=4,EC=6,求AC的长.
(2)解:∵AB是⊙O的切线,
∴∠BDO=90°,
∴BD2+OD2=OB2,∴42+32=(3+BE)2,
∴BE=2,∴BC=BE+EC=8,
∵AD,AC是⊙O的切线,
∴AD=AC,设AD=AC=x,
在Rt△ABC中,AB2=AC2+BC2,
∴(4+x)2=x2+82,解得x=6,∴AC=6.
13.如图,正方形ABCD的边长为4,⊙O的半径为1.若⊙O在正方形ABCD内平移(⊙O可以与该正方形的边相切),则点A到⊙O上的点的距离的最大值为_______.
14.【整体思想求周长】如图,PA,PB切⊙O于点A,B,PA=10,CD切⊙O于点E,交PA,PB于C,D两点,则△PCD的周长是 ( )
A.10
B.18
C.20
D.22
C
15.【三角形外接圆和内切圆综合】如图,点E是△ABC的内心,线段AE的延长线交△ABC的外接圆于点D.
(1)求证:ED=BD;
(1)证明:∵点E是△ABC的内心,
∴∠BAD=∠CAD,∠ABE=∠CBE,
∵∠CBD=∠CAD,
∴∠BAD=∠CBD,
∴∠BED=∠ABE+∠BAD,
∵∠EBD=∠CBE+∠CBD,
∴∠BED=∠EBD,
∴ED=BD;
(2)若∠BAC=90°,△ABC的外接圆⊙O的直径是6,求BD的长.
∵∠BAC=90°,
∴BC是⊙O的直径,∴∠BDC=90°,
∵⊙O的直径是6,
∴BC=6,
∵E为△ABC的内切圆的圆心,
∴∠BAD=∠CAD,∴BD=DC,
∴BD=DC= BC=3 .
(2)解:如图,连接CD,
10 正多边形与圆的相关计算和证明
16. 如图,正△ABC外切于⊙O,正方形DEFG内接于⊙O,若正△ABC的边长为6,则正方形DEFG的边长为_____.
17.如图,在边长为8的菱形ABCD中,∠DAB=60°,以点D为圆心,菱形的高DF为半径画弧,交AD于点E,交CD于点G,则图中阴影部分的面积是 ( )
A.18-3π
B.18- π
C.32 -16π
D.18 -9π
C
18.【利用圆锥公式进行相关计算】如图,在矩形纸片ABCD中,AD=6 cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的底面和侧面,则AB的长为 ( )
A.3.5 cm
B.4 cm
C.4.5 cm
D.5 cm
B
11 圆锥的侧面积与全面积
19.【分类讨论思想——旋转几何体】已知在Rt△ABC中,∠ACB=90°,AC=4,BC=3,以AB边所在的直线为轴,将△ABC旋转一周,则所得几何体的表面积为_______.
20.(2022·江阴月考)如图,AB是⊙O的直径,点C在⊙O上,BD平分∠ABC交⊙O于点D,过点D作DE⊥BC于点E.
(1)求证:DE与⊙O相切;
(1)证明:如图,连接OD.
∵OD=OB,
∴∠ODB=∠OBD.
∵BD平分∠ABC,
∴∠OBD=∠CBD,
∴∠ODB=∠CBD,
∴OD∥BE.
∵BE⊥DE,
∴OD⊥DE.
∵OD是⊙O的半径,
∴DE与⊙O相切;
(2)解:如图,过点D作DH⊥AB于点H.
(2)若AB=10,AD=6,求DE的长;
∵BD平分∠ABC,DE⊥BE,DH⊥AB,
∴DH=DE.
∵AB是⊙O的直径,∴∠ADB=90°.
∵AB=10,AD=6,
∴BD= =8.
∵ AB·DH= AD·DB,
∴DH= ,∴DE=DH= ;
(3)在(2)的条件下,直接写出CD的长为____.
6
(3)解:∵BD平分∠ABC,
∴CD=AD=6.
故答案为6.
∴ ,
21. 如图,四边形ABCD是⊙O的内接四边形,AC为直径, ,DE⊥BC,垂足为E.
(1)求证:CD平分∠ACE;
12 圆综合
∴∠BAD=∠ACD.
∵∠DCE=∠BAD,
∴∠ACD=∠DCE,
即CD平分∠ACE;
(1)证明:∵ ,
(2)解:直线ED与⊙O相切,理由如下:如图,连接OD,
(2)判断直线ED与⊙O的位置关系,并说明理由;
∵OC=OD,
∴∠OCD=∠ODC,
而∠OCD=∠DCE,
∴∠DCE=∠ODC,
∴OD∥BC,
∵DE⊥BC,
∴OD⊥DE,
∴DE为⊙O的切线;
(3)若CE=1,AC=4,求阴影部分的面积.
(3)解:如图,作OH⊥BC于点H,则四边形ODEH为矩形,
∴OD=EH,
∵CE=1,AC=4,
∴OC=OD=2,
∴CH=HE-CE=2-1=1,
在Rt△OHC中,∠HOC=30°,∠COD=60°,
∴阴影部分的面积=S扇形OCD-S△OCD
= .
同课章节目录
