2023-2024学年九年级数学上册第21章 一元二次方程 复习课件(共41张PPT)
文档属性
| 名称 | 2023-2024学年九年级数学上册第21章 一元二次方程 复习课件(共41张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-18 12:17:26 | ||
图片预览











文档简介
(共41张PPT)
2023-2024学年九年级数学上册教学课件★★第二十一章 一元二次方程
1. (2022·海淀区期中)已知m是方程x2+2x-4=0的一个根,求代数式(m+2)2+(m+3)(m-3)的值.
一 运用根的定义求值
解:原式=m2+4m+4+m2-9=2m2+4m-5.
1 整体思想
∵m是方程x2+2x-4=0的一个根,
∴m2+2m-4=0,
即m2+2m=4,
则原式=2(m2+2m)-5=2×4-5=3.
2. (2022·西城区月考)若m是方程x2+x-1=0的一个根,求代数式m3+2m2+2 022的值.
解:根据题意,得m2+m-1=0,
2 降次思想
则m2+m=1,即m(m+1)=1,
则m3+2m2+2 022
=m(m2+m+m)+2 022
=m(m+1)+2 022
=1+2 022=2 023.
3. “a2≥0”这个结论在数学中非常有用,有时我们需要将代数式配成完全平方式.例如:x2+4x+5=x2+4x+4+1=(x+2)2+1,∵(x+2)2≥0,∴(x+2)2+1≥1,∴x2+4x+5≥1.试用“配方法”证明:代数式x2-6x+20的最小值是11.
证明:∵x2-6x+20=(x-3)2+11,
二 配方的应用
1 阅读理解
∴当x=3时,代数式x2-6x+20有最小值,
这个最小值为11.
4. 已知等腰△ABC的三边长为a,b,c,其中a,b满足:a2+b2=6a+12b-45,求△ABC的周长.
2 配方后根据非负性求值
解:a2+b2=6a+12b-45,
a2-6a+9+b2-12b+36=0,
(a-3)2+(b-6)2=0,
∵(a-3)2≥0,(b-6)2≥0,
∴a-3=0,b-6=0,解得,a=3,b=6,
△ABC为等腰三角形,
当a,c为腰时,即c=a=3,这时a+c=3+3=6,a+c=b,不构成三角形;当b,c为腰时,c=b=6,构成三角形.
∴三边长分别为3,6,6,
∴△ABC的周长为3+6+6=15.
5. 用“配方法”证明代数式3x2-5x-1的值总大于2x2-4x-7的值.
3 配方法+作差法比较大小
∴不论x为何值时,3x2-5x-1-(2x2-4x-7)>0总成立,
∴代数式3x2-5x-1的值总大于2x2-4x-7的值.
解:∵3x2-5x-1-(2x2-4x-7)=x2-x+6= +5 >0,
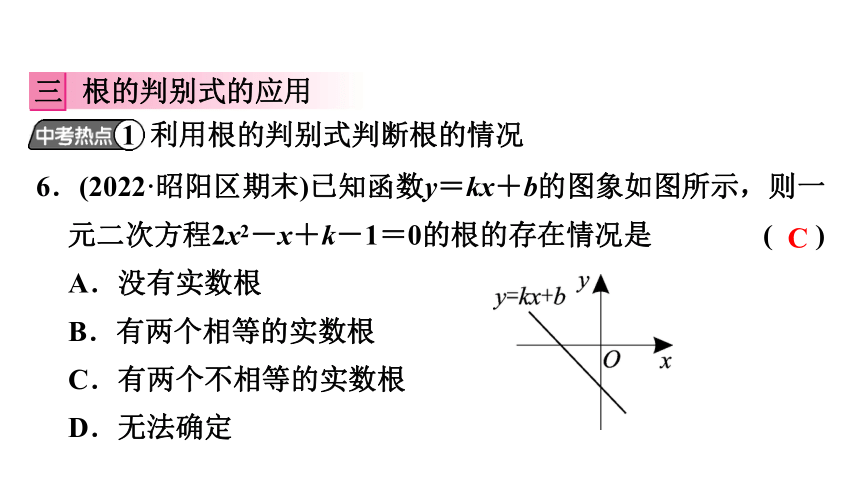
6.(2022·昭阳区期末)已知函数y=kx+b的图象如图所示,则一元二次方程2x2-x+k-1=0的根的存在情况是 ( )
A.没有实数根
B.有两个相等的实数根
C.有两个不相等的实数根
D.无法确定
C
三 根的判别式的应用
1 利用根的判别式判断根的情况
7.等腰三角形的一边长是4,方程x2-6x+m+1=0的两个根是三角形的两边长,则m为 ( )
A.7
B.8
C.4
D.7或8
D
2 根据根的情况,求方程的字母系数的范围或值
解:∵关于x的方程x2-2x+a=0有两个不相等的实数根,
3 利用根的判别式求代数式的值
∴Δ=(-2)2-4a>0,∴a<1.
∴a-1<0,
8. 已知关于x的方程x2-2x+a=0有两个不相等的实数根,请化简 .
∴原式= =a+1-a+1=2.
四 可化为一元二次方程的方程解法
1 可化为一元二次方程的分式方程
9. 解分式方程: =0.6.
解:方程两边同乘以x(x+3),得
26(x+3)-26x=0.6x(x+3)
78=0.6x(x+3)
130=x2+3x
x2+3x-130=0,
x1=-13,x2=10,
经检验,x1=-13,x2=10是原方程的解,
∴原方程的解为x1=-13,x2=10.
2 可化为一元二次方程的方程组
10 . 解方程组
解:
由①,得y=5-x③,
把③代入②,得x2+(5-x)2=17,
整理,得x2-5x+4=0,
解得x1=1,x2=4,
把x1=1,x2=4分别代入③,得y1=4,y2=1.
∴原方程组的解为
3 平方法解无理方程
解:(x-5)2=x-3
x2-10x+25=x-3
x2-11x+28=0
(x-4)(x-7)=0,
x1=4,x2=7,
经检验x=4是原方程的增根,舍去.
∴原方程的解为x=7.
11. 解方程:x-5= .
13. 方程:x2- -1=0的解为_______________.
12. 设a,b是一个直角三角形两条直角边的长,且(a2+b2)(a2+b2-1)=6,则这个直角三角形的斜边长为_____.
4 换元法解方程
5 分类讨论解绝对值方程
x=1或x=-2
14. 已知2- 是方程x2-4x+c=0的一个根,则方程另一个根是_______,c=____.
五 根与系数的关系
1 已知一根,根据韦达定理求另一根
1
15. 已知x1,x2是关于x的方程(m-2)x2+(2m+1)x+m=0两个实数根.
(1)求m的取值范围;
解:(1)依题意,得Δ≥0且m-2≠0,
2 已知两根代数式的值求系数的值
即(2m+1)2-4×(m-2)·m≥0,
解得m≥- 且m≠2;
(2)若 ,求m的值及方程的根.
解:(2)依题意,有以下两种情况:
①当x1=x2,这时Δ=0,得m=- ,
x1=x2= .
②当x1=-x2时,这时x1+x2=0,得m=- ,
∵m≥- 且m≠2,∴此时方程无解.
综上所述,m=- ,x1=x2= .
16.(2022·郾城区期末)已知关于x的一元二次方程x2-(2k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根;
(1)证明:Δ=[-(2k+1)]2-4(k2+k)=1>0,
∴无论k为何值,方程总有两个不相等的实数根.
(2)若△ABC的两边AB,AC的长是这个方程的两个实数根,第三边BC的长为4,当△ABC是等腰三角形时,求k的值.
(2)解:∵Δ=1>0,∴AB≠AC,
∴AB,AC中有一个数为4.
当x=4时,原方程为16-4(2k+1)+k2+k=0,
即k2-7k+12=0,解得k1=3,k2=4.
当k=3时,原方程为x2-7x+12=0,
解得x1=3,x2=4.
∵3,4,4能围成等腰三角形,∴k=3符合题意;
当k=4时,原方程为x2-9x+20=0,
解得x1=4,x2=5.
∵4,4,5能围成等腰三角形,∴k=4符合题意.
综上所述,k的值为3或4.
17.如图,有一道长为10 m的墙,计划用总长为54 m的篱笆,靠墙围成由六个小长方形组成的矩形花圃ABCD.若花圃ABCD面积为72 m2,则AB=____m.
12
六 一元二次方程的应用
1 靠墙问题
2 靠墙开门问题
18. 剧院演出,工作人员准备利用一边靠墙(墙26米)的空旷场地为提前到场的观众设立面积为300平方米的长方形等候区.如图,为了方便观众进出,在两边空出两个宽各为1米的出入口,共用去隔栏绳48米.请问,工作人员围成的这个长方形的相邻两边长分别是多少米?
解:如图,设封闭型长方形等候区的边AB为x米,
依题意,得x(48-2x+2)=300,
整理,得x2-25x+150=0,
解得x1=10,x2=15,
当x=10时,BC=30>26,
当x=15时,BC=20<26,
∴x=10不合题意,应舍去.
答:长方形等候区的边AB为15米,BC为20米.
3 小路问题
19. (2022·西乡塘区期末)某公园准备在一块长为42 m,宽为30 m的长方形花园内修建一个底部为正方形的温室花房(如图),在温室花房四周修四条宽度相同,且与温室花房各边垂直的小路,温室花房边长是小路宽度的6倍,花园内其他的空白地方铺草坪,设小路宽度为x m.
(1)用含x的代数式表示花园内温室花房的面积和小路面积;
解:(1)∵温室花房边长是小路宽度的6倍,小路宽度为x m,
∴温室花房边长为6x m,
∴温室花房的面积为6x·6x=36x2(m2),
小路的面积为(42-6x+30-6x)·x=(72x-12x2)(m2).
答:温室花房的面积为36x2 m2,小路的面积为(72x-12x2) m2;
(2)若草坪面积为1 164 m2时,求这时小路宽度.
解:(2)依题意,得42×30-36x2-(72x-12x2)=1 164.
整理,得x2+3x-4=0.
解得x1=1,x2=-4(不合题意,舍去).
答:当草坪面积为1 164 m2时,小路的宽度为1 m.
20.如图,要设计一幅宽20 cm、长30 cm的图案,其中有两横彩条、一竖彩条,横、竖彩条的宽度比为1∶3.如果要使彩条所占面积是图案总面积的19%,求竖彩条的宽度.
解:设横彩条的宽度是x cm,竖彩条的宽度是3x cm,
则(30-3x)(20-2x)=20×30×(1-19%),
解得x1=1,x2=19(舍去),
所以3x=3.
答:竖彩条的宽度是3 cm.
21. (2022·镇平县期中)李明在家制作一种工艺品,并通过网络平台进行线上销售,经过一段时间后发现:当售价是50元/件时,每天可售出该商品60件,且售价每降低1元,就会多售出2件,设该商品的售价为x元/件(20≤x≤50).
(1)用含售价x的代数式表示每天能售出该工艺品的件数为__________件;
4 利润问题
(160-2x)
解:(1)∵该商品的售价为x元/件(20≤x≤50),且当售价是50元/件时,每天可售出该商品60件,且售价每降低1元,就会多售出2件,
∴每天能售出该工艺品的件数为60+2(50-x)=(160-2x)件.
故答案为(160-2x);
(2)已知每件工艺品需要20元成本,每天销售该工艺品的纯利润为1 000元,求该商品的售价.
解:(2)由题意,得(x-20)(160-2x)=1 000.
整理,得x2-100x+2 100=0.
解得x1=30,x2=70(不合题意,舍去).
答:该商品的售价为30元.
22.(2022·盐都区期中)近年来,区委组织部借助网红直播基地,积极探索党建引领乡村振兴的新模式.某电商在抖音上对种植成本为20元/千克的“阳光玫瑰”葡萄进行直播销售,如果按每千克40元销售,每天可卖出200千克.通过市场调查发现,如果“阳光玫瑰”售价每千克降低1元,日销售量将增加20千克.
(1)若日利润保持不变,每千克“阳光玫瑰”售价可降低多少元?
解:(1)设每千克“阳光玫瑰”售价降低x元,
则每千克的销售利润为(40-x-20)元,
日销售量为(200+20x)千克.
根据题意,得(40-x-20)(200+20x)=(40-20)×200.
整理,得x2-10x=0.
解得x1=0(不合题意,舍去),x2=10.
答:若日利润保持不变,每千克“阳光玫瑰”售价可降低10元;
(2)小明的线下水果店也销售同款葡萄,标价为每千克50元.为提高市场竞争力,促进线下销售,小明决定对该商品实行打折销售,使其销售价格不超过(1)中的售价,则该商品至少需打几折销售?
解:(2)设该商品需要打y折销售,
解得y≤6,
答:该商品至少需打六折销售.
根据题意,得50× ≤40-10.
∴y的最大值为6.
5 动点问题
23. 如图,在矩形ABCD中,AB=6 cm,BC=12 cm,点P从点A沿边AB向点B以1 cm/s的速度移动;同时,点Q从点B沿边BC向点C以2 cm/s的速度移动.问:
(1)几秒时,△PBQ的面积等于8 cm2
解:(1)设x秒后△PBQ的面积等于8 cm2.
则AP=x cm,QB=2x cm,
∴PB=6-x.
解得x1=2,x2=4,
答:2 s或4 s后△PBQ的面积等于8 cm2;
由 ×(6-x)2x=8,
(2)几秒时,△PDQ的面积等于28 cm2
解:(2)设出发x s时△DPQ的面积等于28 cm2.
∵S矩形ABCD-S△APD-S△BPQ-S△CDQ=S△DPQ,
化简整理得x2-6x+8=0,
解得x1=2,x2=4,
答:2 s或4 s后△PDQ的面积等于28 cm2;
∴12×6- ×12x- ×2x(6-x)- ×6×(12-2x)=28,
(3)几秒时,PQ⊥DQ
解:(3)设x s后PQ⊥DQ,∠DQP为直角,
设AP=x,QB=2x,
∴△BPQ∽△CQD,∴ ,
∴ ,
∴2x2-15x+18=0,解得x= 或6,
经检验x= 是原分式方程的根,x=6不是原分式方程的根,当x=6时,点P到达点B、点Q到达点C,此时PQ⊥DQ.
答: s或6 s后PQ⊥DQ.
2023-2024学年九年级数学上册教学课件★★第二十一章 一元二次方程
1. (2022·海淀区期中)已知m是方程x2+2x-4=0的一个根,求代数式(m+2)2+(m+3)(m-3)的值.
一 运用根的定义求值
解:原式=m2+4m+4+m2-9=2m2+4m-5.
1 整体思想
∵m是方程x2+2x-4=0的一个根,
∴m2+2m-4=0,
即m2+2m=4,
则原式=2(m2+2m)-5=2×4-5=3.
2. (2022·西城区月考)若m是方程x2+x-1=0的一个根,求代数式m3+2m2+2 022的值.
解:根据题意,得m2+m-1=0,
2 降次思想
则m2+m=1,即m(m+1)=1,
则m3+2m2+2 022
=m(m2+m+m)+2 022
=m(m+1)+2 022
=1+2 022=2 023.
3. “a2≥0”这个结论在数学中非常有用,有时我们需要将代数式配成完全平方式.例如:x2+4x+5=x2+4x+4+1=(x+2)2+1,∵(x+2)2≥0,∴(x+2)2+1≥1,∴x2+4x+5≥1.试用“配方法”证明:代数式x2-6x+20的最小值是11.
证明:∵x2-6x+20=(x-3)2+11,
二 配方的应用
1 阅读理解
∴当x=3时,代数式x2-6x+20有最小值,
这个最小值为11.
4. 已知等腰△ABC的三边长为a,b,c,其中a,b满足:a2+b2=6a+12b-45,求△ABC的周长.
2 配方后根据非负性求值
解:a2+b2=6a+12b-45,
a2-6a+9+b2-12b+36=0,
(a-3)2+(b-6)2=0,
∵(a-3)2≥0,(b-6)2≥0,
∴a-3=0,b-6=0,解得,a=3,b=6,
△ABC为等腰三角形,
当a,c为腰时,即c=a=3,这时a+c=3+3=6,a+c=b,不构成三角形;当b,c为腰时,c=b=6,构成三角形.
∴三边长分别为3,6,6,
∴△ABC的周长为3+6+6=15.
5. 用“配方法”证明代数式3x2-5x-1的值总大于2x2-4x-7的值.
3 配方法+作差法比较大小
∴不论x为何值时,3x2-5x-1-(2x2-4x-7)>0总成立,
∴代数式3x2-5x-1的值总大于2x2-4x-7的值.
解:∵3x2-5x-1-(2x2-4x-7)=x2-x+6= +5 >0,
6.(2022·昭阳区期末)已知函数y=kx+b的图象如图所示,则一元二次方程2x2-x+k-1=0的根的存在情况是 ( )
A.没有实数根
B.有两个相等的实数根
C.有两个不相等的实数根
D.无法确定
C
三 根的判别式的应用
1 利用根的判别式判断根的情况
7.等腰三角形的一边长是4,方程x2-6x+m+1=0的两个根是三角形的两边长,则m为 ( )
A.7
B.8
C.4
D.7或8
D
2 根据根的情况,求方程的字母系数的范围或值
解:∵关于x的方程x2-2x+a=0有两个不相等的实数根,
3 利用根的判别式求代数式的值
∴Δ=(-2)2-4a>0,∴a<1.
∴a-1<0,
8. 已知关于x的方程x2-2x+a=0有两个不相等的实数根,请化简 .
∴原式= =a+1-a+1=2.
四 可化为一元二次方程的方程解法
1 可化为一元二次方程的分式方程
9. 解分式方程: =0.6.
解:方程两边同乘以x(x+3),得
26(x+3)-26x=0.6x(x+3)
78=0.6x(x+3)
130=x2+3x
x2+3x-130=0,
x1=-13,x2=10,
经检验,x1=-13,x2=10是原方程的解,
∴原方程的解为x1=-13,x2=10.
2 可化为一元二次方程的方程组
10 . 解方程组
解:
由①,得y=5-x③,
把③代入②,得x2+(5-x)2=17,
整理,得x2-5x+4=0,
解得x1=1,x2=4,
把x1=1,x2=4分别代入③,得y1=4,y2=1.
∴原方程组的解为
3 平方法解无理方程
解:(x-5)2=x-3
x2-10x+25=x-3
x2-11x+28=0
(x-4)(x-7)=0,
x1=4,x2=7,
经检验x=4是原方程的增根,舍去.
∴原方程的解为x=7.
11. 解方程:x-5= .
13. 方程:x2- -1=0的解为_______________.
12. 设a,b是一个直角三角形两条直角边的长,且(a2+b2)(a2+b2-1)=6,则这个直角三角形的斜边长为_____.
4 换元法解方程
5 分类讨论解绝对值方程
x=1或x=-2
14. 已知2- 是方程x2-4x+c=0的一个根,则方程另一个根是_______,c=____.
五 根与系数的关系
1 已知一根,根据韦达定理求另一根
1
15. 已知x1,x2是关于x的方程(m-2)x2+(2m+1)x+m=0两个实数根.
(1)求m的取值范围;
解:(1)依题意,得Δ≥0且m-2≠0,
2 已知两根代数式的值求系数的值
即(2m+1)2-4×(m-2)·m≥0,
解得m≥- 且m≠2;
(2)若 ,求m的值及方程的根.
解:(2)依题意,有以下两种情况:
①当x1=x2,这时Δ=0,得m=- ,
x1=x2= .
②当x1=-x2时,这时x1+x2=0,得m=- ,
∵m≥- 且m≠2,∴此时方程无解.
综上所述,m=- ,x1=x2= .
16.(2022·郾城区期末)已知关于x的一元二次方程x2-(2k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根;
(1)证明:Δ=[-(2k+1)]2-4(k2+k)=1>0,
∴无论k为何值,方程总有两个不相等的实数根.
(2)若△ABC的两边AB,AC的长是这个方程的两个实数根,第三边BC的长为4,当△ABC是等腰三角形时,求k的值.
(2)解:∵Δ=1>0,∴AB≠AC,
∴AB,AC中有一个数为4.
当x=4时,原方程为16-4(2k+1)+k2+k=0,
即k2-7k+12=0,解得k1=3,k2=4.
当k=3时,原方程为x2-7x+12=0,
解得x1=3,x2=4.
∵3,4,4能围成等腰三角形,∴k=3符合题意;
当k=4时,原方程为x2-9x+20=0,
解得x1=4,x2=5.
∵4,4,5能围成等腰三角形,∴k=4符合题意.
综上所述,k的值为3或4.
17.如图,有一道长为10 m的墙,计划用总长为54 m的篱笆,靠墙围成由六个小长方形组成的矩形花圃ABCD.若花圃ABCD面积为72 m2,则AB=____m.
12
六 一元二次方程的应用
1 靠墙问题
2 靠墙开门问题
18. 剧院演出,工作人员准备利用一边靠墙(墙26米)的空旷场地为提前到场的观众设立面积为300平方米的长方形等候区.如图,为了方便观众进出,在两边空出两个宽各为1米的出入口,共用去隔栏绳48米.请问,工作人员围成的这个长方形的相邻两边长分别是多少米?
解:如图,设封闭型长方形等候区的边AB为x米,
依题意,得x(48-2x+2)=300,
整理,得x2-25x+150=0,
解得x1=10,x2=15,
当x=10时,BC=30>26,
当x=15时,BC=20<26,
∴x=10不合题意,应舍去.
答:长方形等候区的边AB为15米,BC为20米.
3 小路问题
19. (2022·西乡塘区期末)某公园准备在一块长为42 m,宽为30 m的长方形花园内修建一个底部为正方形的温室花房(如图),在温室花房四周修四条宽度相同,且与温室花房各边垂直的小路,温室花房边长是小路宽度的6倍,花园内其他的空白地方铺草坪,设小路宽度为x m.
(1)用含x的代数式表示花园内温室花房的面积和小路面积;
解:(1)∵温室花房边长是小路宽度的6倍,小路宽度为x m,
∴温室花房边长为6x m,
∴温室花房的面积为6x·6x=36x2(m2),
小路的面积为(42-6x+30-6x)·x=(72x-12x2)(m2).
答:温室花房的面积为36x2 m2,小路的面积为(72x-12x2) m2;
(2)若草坪面积为1 164 m2时,求这时小路宽度.
解:(2)依题意,得42×30-36x2-(72x-12x2)=1 164.
整理,得x2+3x-4=0.
解得x1=1,x2=-4(不合题意,舍去).
答:当草坪面积为1 164 m2时,小路的宽度为1 m.
20.如图,要设计一幅宽20 cm、长30 cm的图案,其中有两横彩条、一竖彩条,横、竖彩条的宽度比为1∶3.如果要使彩条所占面积是图案总面积的19%,求竖彩条的宽度.
解:设横彩条的宽度是x cm,竖彩条的宽度是3x cm,
则(30-3x)(20-2x)=20×30×(1-19%),
解得x1=1,x2=19(舍去),
所以3x=3.
答:竖彩条的宽度是3 cm.
21. (2022·镇平县期中)李明在家制作一种工艺品,并通过网络平台进行线上销售,经过一段时间后发现:当售价是50元/件时,每天可售出该商品60件,且售价每降低1元,就会多售出2件,设该商品的售价为x元/件(20≤x≤50).
(1)用含售价x的代数式表示每天能售出该工艺品的件数为__________件;
4 利润问题
(160-2x)
解:(1)∵该商品的售价为x元/件(20≤x≤50),且当售价是50元/件时,每天可售出该商品60件,且售价每降低1元,就会多售出2件,
∴每天能售出该工艺品的件数为60+2(50-x)=(160-2x)件.
故答案为(160-2x);
(2)已知每件工艺品需要20元成本,每天销售该工艺品的纯利润为1 000元,求该商品的售价.
解:(2)由题意,得(x-20)(160-2x)=1 000.
整理,得x2-100x+2 100=0.
解得x1=30,x2=70(不合题意,舍去).
答:该商品的售价为30元.
22.(2022·盐都区期中)近年来,区委组织部借助网红直播基地,积极探索党建引领乡村振兴的新模式.某电商在抖音上对种植成本为20元/千克的“阳光玫瑰”葡萄进行直播销售,如果按每千克40元销售,每天可卖出200千克.通过市场调查发现,如果“阳光玫瑰”售价每千克降低1元,日销售量将增加20千克.
(1)若日利润保持不变,每千克“阳光玫瑰”售价可降低多少元?
解:(1)设每千克“阳光玫瑰”售价降低x元,
则每千克的销售利润为(40-x-20)元,
日销售量为(200+20x)千克.
根据题意,得(40-x-20)(200+20x)=(40-20)×200.
整理,得x2-10x=0.
解得x1=0(不合题意,舍去),x2=10.
答:若日利润保持不变,每千克“阳光玫瑰”售价可降低10元;
(2)小明的线下水果店也销售同款葡萄,标价为每千克50元.为提高市场竞争力,促进线下销售,小明决定对该商品实行打折销售,使其销售价格不超过(1)中的售价,则该商品至少需打几折销售?
解:(2)设该商品需要打y折销售,
解得y≤6,
答:该商品至少需打六折销售.
根据题意,得50× ≤40-10.
∴y的最大值为6.
5 动点问题
23. 如图,在矩形ABCD中,AB=6 cm,BC=12 cm,点P从点A沿边AB向点B以1 cm/s的速度移动;同时,点Q从点B沿边BC向点C以2 cm/s的速度移动.问:
(1)几秒时,△PBQ的面积等于8 cm2
解:(1)设x秒后△PBQ的面积等于8 cm2.
则AP=x cm,QB=2x cm,
∴PB=6-x.
解得x1=2,x2=4,
答:2 s或4 s后△PBQ的面积等于8 cm2;
由 ×(6-x)2x=8,
(2)几秒时,△PDQ的面积等于28 cm2
解:(2)设出发x s时△DPQ的面积等于28 cm2.
∵S矩形ABCD-S△APD-S△BPQ-S△CDQ=S△DPQ,
化简整理得x2-6x+8=0,
解得x1=2,x2=4,
答:2 s或4 s后△PDQ的面积等于28 cm2;
∴12×6- ×12x- ×2x(6-x)- ×6×(12-2x)=28,
(3)几秒时,PQ⊥DQ
解:(3)设x s后PQ⊥DQ,∠DQP为直角,
设AP=x,QB=2x,
∴△BPQ∽△CQD,∴ ,
∴ ,
∴2x2-15x+18=0,解得x= 或6,
经检验x= 是原分式方程的根,x=6不是原分式方程的根,当x=6时,点P到达点B、点Q到达点C,此时PQ⊥DQ.
答: s或6 s后PQ⊥DQ.
同课章节目录
