2023-2024学年九年级数学上册 第22章 二次函数 复习课件(共62张PPT)
文档属性
| 名称 | 2023-2024学年九年级数学上册 第22章 二次函数 复习课件(共62张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-18 12:18:44 | ||
图片预览







文档简介
(共62张PPT)
2023-2024学年九年级数学上册教学课件★★第二十二章 二次函数
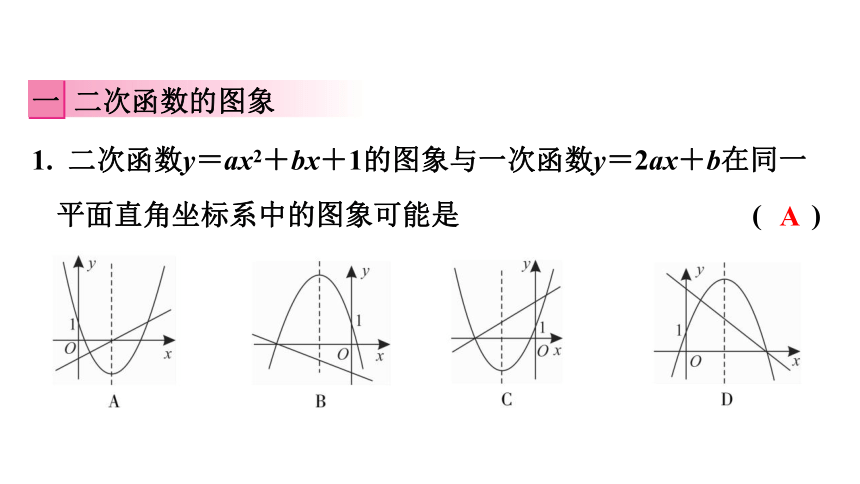
1. 二次函数y=ax2+bx+1的图象与一次函数y=2ax+b在同一平面直角坐标系中的图象可能是 ( )
A
一 二次函数的图象
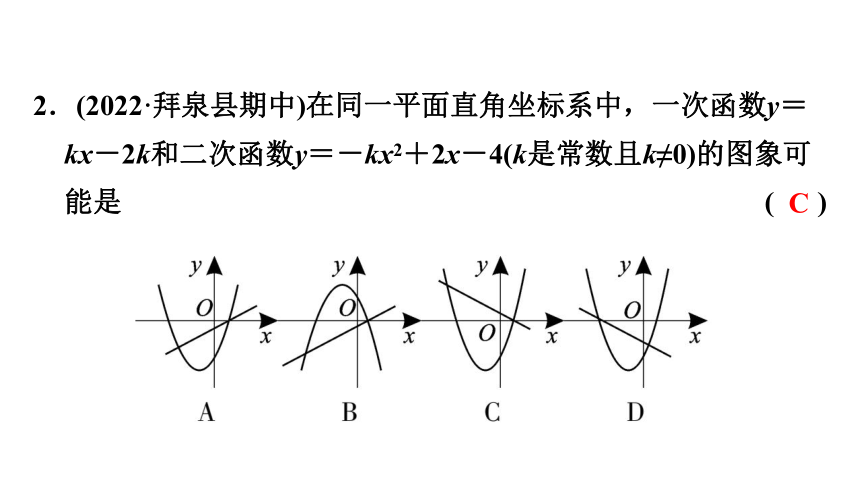
2.(2022·拜泉县期中)在同一平面直角坐标系中,一次函数y=kx-2k和二次函数y=-kx2+2x-4(k是常数且k≠0)的图象可能是 ( )
C
3. 已知抛物线y=ax2+bx+c,如图,直线x=-1是其对称轴,与x轴的一个交点为(-3,0).
(1)判断符号:a___0,b___0,c___0,b2-4ac___0,a-b+c___0;a+b+c___0.
(2)当x满足_______________时,y<0.
<
二 抛物线中a,b和c的几何意义
<
>
>
>
=
x>1或x<-3
4.(2022·定南县期中)如图,抛物线y=ax2+bx+c的对称轴是直线x=-1,且过点 ,有下列结论:①abc>0;②a-2b+4c=0;③3b+2c>0;④a-b≥m(am-b),其中正确的结论为 ( )
A.①②
B.②③
C.③④
D.①④
D
三 二次函数的应用
1 复杂靠墙问题
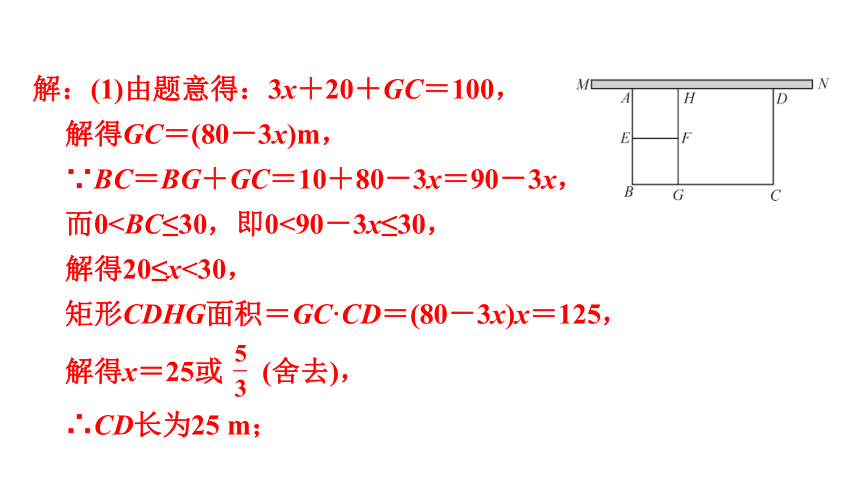
5. 一段长为30 m的墙MN前有一块矩形ABCD空地,用100 m长的篱笆围成如图所示的图形(靠墙的一边不用篱笆,篱笆的厚度忽略不计),其中四边形AEFH和四边形CDHG是矩形,四边形EBGF是边长为10 m的正方形,设CD=x m.
(1)若矩形CDHG面积为125 m2,求CD长;
解:(1)由题意得:3x+20+GC=100,
解得GC=(80-3x)m,
∵BC=BG+GC=10+80-3x=90-3x,
而0解得20≤x<30,
矩形CDHG面积=GC·CD=(80-3x)x=125,
∴CD长为25 m;
解得x=25或 (舍去),
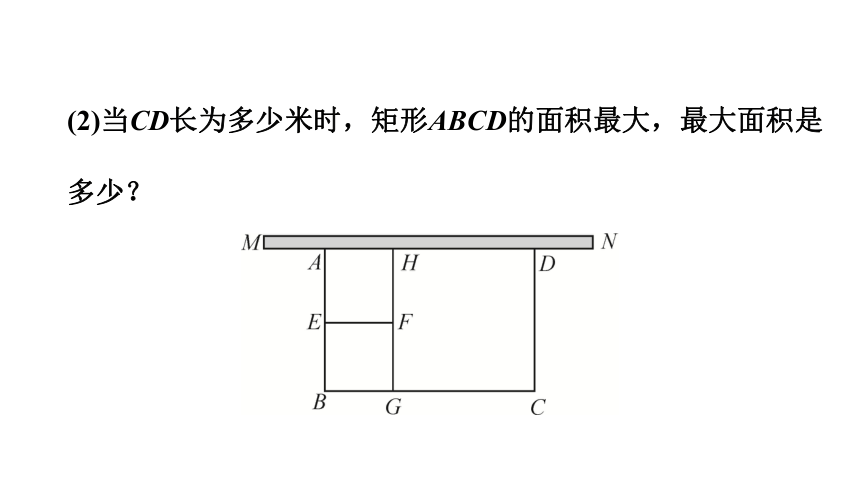
(2)当CD长为多少米时,矩形ABCD的面积最大,最大面积是多少?
解:(2)设矩形ABCD的面积为s,
则s=BC·CD=x(90-3x)=-3x2+90x=-3(x-15)2+675,
∵-3<0,故抛物线开口向下,
而20≤x<30,当x>15时,s随x的增大而减小,
故当x=20(m)时,s取得最大值为
-3×(20-15)2+675=600(m2).
答:当CD长为20 m时,矩形ABCD的面积最大,最大面积是600 m2.
2 销售问题
6. (2022·浠水县期中)小丽老师家有一片80棵桃树的桃园,现准备多种一些桃树提高桃园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低,若该桃园每棵桃树产桃y(单位:千克)与增种桃树x(单位:棵)之间的函数关系如图所示.
(1)求y与x之间的函数关系式;
解:(1)设函数的表达式为y=kx+b,
该一次函数过点(12,74),(28,66),
得
解得
∴该函数的表达式为y=- x+80;
(2)在投入成本最低的情况下,增种桃树多少棵时,桃园的总产量可以达到6 750千克?
解:(2)根据题意,得(-0.5x+80)(80+x)=6 750.
解得x1=10,x2=70.
∵投入成本最低,
∴x2=70不符合题意,舍去.
∴增种桃树10棵时,桃园的总产量可以达到6 750千克;
(3)如果增种的桃树x满足:20≤x≤40,请你帮小丽老师家计算一下,桃园的总产量最少是多少千克?
解:(3)根据题意,得
w=(-0.5x+80)(80+x)
=-0.5x2+40x+6 400
=-0.5(x-40)2+7 200.
∵a=-0.5<0,
∴抛物线开口向下,函数有最大值.
∵20≤x≤40,
∴当x=20时,w最小值=7 000千克,
∴桃园的总产量最少是7 000千克.
7.某商家正在热销一种商品,其成本为30元/件,在销售过程中发现随着售价增加,销售量在减少.商家决定当售价为60元/件时,改变销售策略,此时售价每增加1元需支付由此产生的额外费用150元.该商品销售量y(件)与售价x(元/件)满足如图所示的函数关系(其中40≤x≤70,且x为整数).
(1)直接写出y与x的函数关系式;
解:(1)设线段AB的表达式为y=kx+b(40≤x≤60),
将点(40,300),(60,100)代入
∴函数的表达式为y=-10x+700(40≤x≤60),
设线段BC的表达式为y=mx+n(60将点(60,100),(70,150)代入
∴函数的表达式为y=5x-200(60得 解得
得 解得
∴y与x的函数关系式为y=
(2)当售价为多少时,商家所获利润最大,最大利润是多少?
解:(2)设获得的利润为w元,
①当40≤x≤60时,
w=(x-30)(-10x+700)=-10(x-50)2+4 000,
∵-10<0,
∴当x=50时,w有最大值,最大值为4 000元;
②当60w=(x-30)(5x-200)-150(x-60)=5(x-50)2+2 500,
∵5>0,∴当60∴当x=70时,w有最大,
最大值为5(70-50)2+2 500=4 500(元),
综上,当售价为70元时,该商家获得的利润最大,最大利润为4 500元.
8. 如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于点A(-1,0),B(3,0),与y轴交于点C.
(1)b=_____,c=_____;
-2
四 二次函数的综合
1 面积问题,求PA+PB最小值
-3
解:(1)∵点A和点B在二次函数y=x2+bx+c图象上,
故答案为-2,-3;
则 解得
(2)若点D在该二次函数的图象上,且S△ABD=2S△ABC,求点D的坐标;
解:(2)如图,连接BC,
依题意,得A(-1,0),B(3,0),C(0,-3),
y=x2-2x-3,
∵S△ABD=2S△ABC,设点D(m,m2-2m-3),
可得,y值都为6,
∴S△ABC= = ×4×3=6,
∴ ×AB× =2×6,即 ×4× =2×6,
解得:m=1+ 或1- ,代入y=x2-2x-3,
∴D点坐标为(1+ ,6)或(1- ,6);
(3)若点P在抛物线的对称轴上,求PA+PC的最小值.
解:(3)设BC交对称轴于点P,
此时,PA+PC最小,最小值为BC的长BC= ,
故PA+PC的最小值为3 .
9.(2022·浠水县期中)如图1,抛物线y=-x2+bx+c与x轴交于A(1,0),B(-3,0)两点.
(1)求该抛物线的解析式;
解:(1)将点A,B代入抛物线,得
将①-②,得8+4b=0,
∴b=-2,
代入①,得c=1-b=3,
∴y=-x2-2x+3;
(2)设抛物线与y轴交于点C,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出点Q的坐标;若不存在,请说明理由;
如图1,由抛物线性质可知点A关于x=-1的对称点为B,
解:(2)令x=0,∴y=3,∴C(0,3),∴对称轴x=-1.
∴AQ+QC=BQ+QC≥BC(三角形两边之和大于第三边,Q在BC上时取等号)
∴△QAC周长最小时,Q为BC与x=-1的交点.
②代入①,得k=1,∴y=x+3.
令x=-1,得y=2,∴Q(-1,2);
设lBC:y=kx+b,代入B,C,得
(3)如图2,P是线段BC上的一个动点.过点P作y轴的平行线交抛物线于点E,求线段PE长度的最大值.
解:(3)设P(m,m+3)(-3≤m≤0),点P在线段BC上,
∴E(m,-m2-2m+3).
∵PE∥y轴,E在抛物线上,
∴PE=-m2-2m+3-(m+3)=-m2-3m
= ,
故PE最大值为 .
10. (2022·雁塔区四模)抛物线W:y=ax2+bx+3(a≠0)与x轴交于A(1,0),B(4,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
解:(1)∵y=ax2+bx+3(a≠0)与x轴交于A(1,0),B(4,0),
2 与等腰三角形,特殊四边形综合
∴ 解得
∴抛物线的解析式为y= x2- x+3;
(2)已知点P为x轴上一点,是否存在这样的点P,使得△BCP是以CP为腰的等腰三角形,若存在,请求出点P的坐标;若不存在,请说明理由.
∴点C(0,3).
设点P(x,0),由点C,B,P的坐标,得
CP2=x2+32,PB2=(x-4)2,CB2=42+32=25,
当PC=CB时,x2+32=25,解得x=4(舍去)或-4;
解:(2)∵抛物线的解析式为y= x2- x+3,
∴点P的坐标为 或(-4,0).
当PC=PB时,即x2+32=(x-4)2.解得x= ;
11.(2022·番禺区期中)如图,抛物线y=- x2+bx+c与x轴交于点A,B,与y轴交于点C.直线y=2x+2经过点A,C.
(1)抛物线的解析式为____________________,点B的坐标为______;
(4,0)
解:(1)对于y=2x+2,令y=2x+2=0,解得x=-1;
令x=0,则y=2,故点A,C的坐标分别为(-1,0),(0,2).
将点A,C的坐标代入抛物线表达式,得
解得x=4或-1,故点B(4,0).
解得
故抛物线的表达式为y=- x2+ x+2. ①
令y=- x2+ x+2=0,
故答案为y=- x2+ x+2,(4,0);
(2)若点P是第一象限内抛物线上一点,连接BP并延长交直线AC于点E,当CE=AC时,求点P的横坐标;
解:(2)由点A,B,C的坐标知,
AB=5,AC2=5,BC2=20,即AB2=AC2+BC2,
∴△ABC为直角三角形,即BC⊥AE.
而CE=AC,故AB=EB=5.
设点E(m,2m+2),则(m-4)2+(2m+2)2=25,
解得m=-1(舍去)或1,故点E(1,4).
由B,E的坐标,得直线BE的表达式为y=- x+ . ②
联立①②并解得x=4(舍去)或 ,
即点P的横坐标为 ;
(3)若点G是抛物线上一点,点H是x轴上一点,是否存在这样的点G,H,使以点A,C,G,H为顶点的四边形是平行四边形?若存在,请求出点G的坐标;若不存在,请说明理由.
当AC是平行四边形的对角线时,
由中点坐标公式,得0+2=n+0,解得n=2,
当AH是平行四边形的对角线时,
当AG是平行四边形的对角线时,同理可得,点G(3,2).
解:(3)存在.理由如下:设点G(m,n),n=- m2+ m+2.
即n=- m2+ m+2=2,解得m=0(舍去)或3,即点G(3,2);
同理可得0+0=n+2,解得n=-2,则点G ;
综上所述,点G的坐标为 或G(3,2).
12. 如图1,抛物线y=ax2+c与x轴交于点A,B,与y轴交于点C,P为x轴下方抛物线上一点,若OC=2OA=4.
(1)求抛物线解析式;
3 二次函数与角度
解:(1)∵OC=4,∴c=-4,
∴抛物线的解析式为y=ax2-4,
∵OC=2OA=4,∴A(-2,0),
∴0=4a-4,解得a=1,
∴抛物线的解析式为y=x2-4;
(2)如图2,若∠ABP=∠ACO,求点P的坐标.
解:(2)如图2,过点A作x轴的垂线交BP的延长线于点Q.
∴△BAQ≌△COA(ASA),∴AQ=OA=2,∴Q(-2,-2).
∵B(2,0),Q(-2,-2),
在△BAQ和△COA中,
∴直线BQ的解析式为y= x-1,
联立 解得 (舍去)或
∴点P坐标为 .
13.(2022·云安区模拟)如图,在平面直角坐标系中,已知抛物线y=-x2+bx+c与x轴交于A,B(4,0)两点,与y轴交于点C,点D(3,4)在抛物线上,点P是抛物线上一动点.
(1)求该抛物线的解析式;
解:(1)∵点B(4,0),
点D(3,4)在抛物线y=-x2+bx+c上,
∴该抛物线的解析式为y=-x2+3x+4;
∴
解得
(2)如图1,连接OD,若OP平分∠COD,求点P的坐标;
①当点P在第一象限时,作PE∥y轴,交OD于点Q,交x轴于点E.
解:(2)如图1,分两种情况讨论:
∵PE∥y轴,∴∠OPQ=∠POC.
∵OP平分∠COD,∴∠POC=∠POQ,
∴∠POQ=∠OPQ,∴PQ=OQ.
设点P的横坐标为t,则P(t,-t2+3t+4),
设OD的解析式为y=kx,将D(3,4)代入,得k= ,
∴OD的解析式为y= x.
②延长PO交抛物线于点P′,由图1可知,点P′也符合题意.
解得t1=2,t2=-2(舍去),∴t=2,
∴-t2+3t+4=-4+6+4=6,
∴点P的坐标为(2,6);
由点P(2,6)可得直线OP的解析式为y=3x.
Q ,E(t,0),其中0∴PQ=-t2+3t+4- t=-t2+ t+4,OE=t,EQ= t,
∴OQ= = t.∴ t=-t2+ t+4,
∴点P′(-2,-6).
综上所述,点P的坐标是(2,6)或(-2,-6);
联立 解得
(3)如图2,连接AC,BC,抛物线上是否存在点P,使∠CBP+∠ACO=45°?若存在,请直接写出点P的坐标;若不存在,请说明理由.
解:(3)如图2,过点B作∠ABP=∠ACO,
交y轴正半轴于点F,交抛物线于点P,
则∠CBP+∠ACO=∠CBP+∠ABP=∠ABC=45°.
∵∠OBF=∠OCA,OB=OC,∠BOF=∠COA=90°,
∴△OBF≌△OCA,∴OF=OA=1,∴F(0,1).
设直线BF的解析式为y=mx+n,
将B(4,0),F(0,1)代入,得 解得
∴直线BF的解析式为y=- x+1,
由对称的性质,得∠F′CB=∠FCB=45°,
CF′=CF=OC-OF=3,∠CBF′=∠CBF.
∴点P′也符合题意.
∵∠F′CB=∠OBC=45°,
∴CF′∥OB,∴F′(3,4).
联立 解得 或 ∴P ;
如图2,作点F关于直线BC的对称点F′,作射线BF′交抛物线于点P′,
由点B(4,0)和点F′(3,4)可得直线BF′的解析式为
y=-4x+16,
∴点P′的坐标是(3,4).
联立 解得 或
综上所述,点P的坐标是 或(3,4).
4 求三角形面积最大值
14. 如图,抛物线y=x2+bx+c与x轴交于点A(-1,0),与y轴交于点C(0,-3).
(1)求该抛物线的解析式及顶点坐标;
解:(1)把点A(-1,0),点C(0,-3)代入抛物线的解析式得
∴抛物线的解析式为y=x2-2x-3,
∵y=x2-2x-3=(x-1)2-4,
∴顶点的坐标为(1,-4);
解得
(2)若P是线段OB上一动点,过P作y轴的平行线交抛物线于点H,交BC于点N,设OP=t,△BCH的面积为S,求S关于t的函数关系式.若S有最大值,请求出S的最大值;若没有,请说明理由.
解:(2)如图,设直线BC的解析式为y=kx+d(k≠0),
在抛物线上,当y=0时,即x2-2x-3=0,
解得:x1=3,x2=-1,∴B(3,0),
将B(3,0),C(0,-3)代入y=kx+d(k≠0)中,
∴直线BC的解析式为y=x-3,
∵OP=t,B(3,0),∴OB=3,
设点P的坐标为(t,0),
得 解得
则点N的坐标为(t,t-3),点H的坐标为(t,t2-2t-3),
∴NH=t-3-(t2-2t-3)=-t2+3t,
∴S=S△BCH=S△BNH+S△CNH= NH·OB= ×3(-t2+3t)
=- t2+ t=-
∵0≤t≤3,- <0,∴S有最大值,
∴当t= 时,S取最大值,最大值为 .
15. (2022·东营区模拟)如图,已知抛物线y=-x2+2x+3 与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,连接BC.
(1)求A,B,C三点的坐标;
解:(1)对于y=-x2+2x+3,
5 二次函数与直角三角形综合
令x=0,则y=3,∴C(0,3),
令y=0,则y=-x2+2x+3=0,
解得x1=3,x2=-1,
∴A(-1,0),B(3,0);
(2)若点P为线段BC上的一点(不与B,C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当线段PM的长度最大时,求点M的坐标;
解:(2)设BC的表达式为y=kx+b,
∴直线BC的表达式为y=-x+3.
设点P的坐标为(t,-t+3),
则点M的坐标为(t,-t2+2t+3),
则 解得
∴PM=-t2+2t+3+t-3=-t2+3t=- + ,
当t= 时,PM最大,此时点M的坐标为 ;
(3)在(2)的条件下,当线段PM的长度最大时,在抛物线的对称轴上有一点Q,使得△CNQ为直角三角形,直接写出点Q的坐标.
解:(3)∵y=-x2+2x+3=-(x-1)2+4,
∴抛物线的对称轴为直线x=1,
∵△CNQ为直角三角形,
∴分点C为直角顶点、点Q为直角顶点和点N为直角顶点三种情况:
∴设Q(1,m),且C(0,3),N ,
∴CN= ,CQ= ,
NQ= .
①当点C为直角顶点时,则有CN2+CQ2=NQ2,
②当点Q为直角顶点时,则有CQ2+NQ2=CN2,
即 +(m2-6m+10)=m2+ ,解得m= ,
此时点Q的坐标为 ;
即(m2-6m+10)+m2+ = ,
解得m1= ,m2= ,
③当点N为直角顶点时,则有CN2+NQ2=CQ2,
此时点Q的坐标为 或 ;
即 +m2+ =(m2-6m+10),
解得m=- ,此时点Q的坐标为 .
综上所述,点Q坐标为 或 或 或
.
2023-2024学年九年级数学上册教学课件★★第二十二章 二次函数
1. 二次函数y=ax2+bx+1的图象与一次函数y=2ax+b在同一平面直角坐标系中的图象可能是 ( )
A
一 二次函数的图象
2.(2022·拜泉县期中)在同一平面直角坐标系中,一次函数y=kx-2k和二次函数y=-kx2+2x-4(k是常数且k≠0)的图象可能是 ( )
C
3. 已知抛物线y=ax2+bx+c,如图,直线x=-1是其对称轴,与x轴的一个交点为(-3,0).
(1)判断符号:a___0,b___0,c___0,b2-4ac___0,a-b+c___0;a+b+c___0.
(2)当x满足_______________时,y<0.
<
二 抛物线中a,b和c的几何意义
<
>
>
>
=
x>1或x<-3
4.(2022·定南县期中)如图,抛物线y=ax2+bx+c的对称轴是直线x=-1,且过点 ,有下列结论:①abc>0;②a-2b+4c=0;③3b+2c>0;④a-b≥m(am-b),其中正确的结论为 ( )
A.①②
B.②③
C.③④
D.①④
D
三 二次函数的应用
1 复杂靠墙问题
5. 一段长为30 m的墙MN前有一块矩形ABCD空地,用100 m长的篱笆围成如图所示的图形(靠墙的一边不用篱笆,篱笆的厚度忽略不计),其中四边形AEFH和四边形CDHG是矩形,四边形EBGF是边长为10 m的正方形,设CD=x m.
(1)若矩形CDHG面积为125 m2,求CD长;
解:(1)由题意得:3x+20+GC=100,
解得GC=(80-3x)m,
∵BC=BG+GC=10+80-3x=90-3x,
而0
矩形CDHG面积=GC·CD=(80-3x)x=125,
∴CD长为25 m;
解得x=25或 (舍去),
(2)当CD长为多少米时,矩形ABCD的面积最大,最大面积是多少?
解:(2)设矩形ABCD的面积为s,
则s=BC·CD=x(90-3x)=-3x2+90x=-3(x-15)2+675,
∵-3<0,故抛物线开口向下,
而20≤x<30,当x>15时,s随x的增大而减小,
故当x=20(m)时,s取得最大值为
-3×(20-15)2+675=600(m2).
答:当CD长为20 m时,矩形ABCD的面积最大,最大面积是600 m2.
2 销售问题
6. (2022·浠水县期中)小丽老师家有一片80棵桃树的桃园,现准备多种一些桃树提高桃园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低,若该桃园每棵桃树产桃y(单位:千克)与增种桃树x(单位:棵)之间的函数关系如图所示.
(1)求y与x之间的函数关系式;
解:(1)设函数的表达式为y=kx+b,
该一次函数过点(12,74),(28,66),
得
解得
∴该函数的表达式为y=- x+80;
(2)在投入成本最低的情况下,增种桃树多少棵时,桃园的总产量可以达到6 750千克?
解:(2)根据题意,得(-0.5x+80)(80+x)=6 750.
解得x1=10,x2=70.
∵投入成本最低,
∴x2=70不符合题意,舍去.
∴增种桃树10棵时,桃园的总产量可以达到6 750千克;
(3)如果增种的桃树x满足:20≤x≤40,请你帮小丽老师家计算一下,桃园的总产量最少是多少千克?
解:(3)根据题意,得
w=(-0.5x+80)(80+x)
=-0.5x2+40x+6 400
=-0.5(x-40)2+7 200.
∵a=-0.5<0,
∴抛物线开口向下,函数有最大值.
∵20≤x≤40,
∴当x=20时,w最小值=7 000千克,
∴桃园的总产量最少是7 000千克.
7.某商家正在热销一种商品,其成本为30元/件,在销售过程中发现随着售价增加,销售量在减少.商家决定当售价为60元/件时,改变销售策略,此时售价每增加1元需支付由此产生的额外费用150元.该商品销售量y(件)与售价x(元/件)满足如图所示的函数关系(其中40≤x≤70,且x为整数).
(1)直接写出y与x的函数关系式;
解:(1)设线段AB的表达式为y=kx+b(40≤x≤60),
将点(40,300),(60,100)代入
∴函数的表达式为y=-10x+700(40≤x≤60),
设线段BC的表达式为y=mx+n(60
∴函数的表达式为y=5x-200(60
得 解得
∴y与x的函数关系式为y=
(2)当售价为多少时,商家所获利润最大,最大利润是多少?
解:(2)设获得的利润为w元,
①当40≤x≤60时,
w=(x-30)(-10x+700)=-10(x-50)2+4 000,
∵-10<0,
∴当x=50时,w有最大值,最大值为4 000元;
②当60
∵5>0,∴当60
最大值为5(70-50)2+2 500=4 500(元),
综上,当售价为70元时,该商家获得的利润最大,最大利润为4 500元.
8. 如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于点A(-1,0),B(3,0),与y轴交于点C.
(1)b=_____,c=_____;
-2
四 二次函数的综合
1 面积问题,求PA+PB最小值
-3
解:(1)∵点A和点B在二次函数y=x2+bx+c图象上,
故答案为-2,-3;
则 解得
(2)若点D在该二次函数的图象上,且S△ABD=2S△ABC,求点D的坐标;
解:(2)如图,连接BC,
依题意,得A(-1,0),B(3,0),C(0,-3),
y=x2-2x-3,
∵S△ABD=2S△ABC,设点D(m,m2-2m-3),
可得,y值都为6,
∴S△ABC= = ×4×3=6,
∴ ×AB× =2×6,即 ×4× =2×6,
解得:m=1+ 或1- ,代入y=x2-2x-3,
∴D点坐标为(1+ ,6)或(1- ,6);
(3)若点P在抛物线的对称轴上,求PA+PC的最小值.
解:(3)设BC交对称轴于点P,
此时,PA+PC最小,最小值为BC的长BC= ,
故PA+PC的最小值为3 .
9.(2022·浠水县期中)如图1,抛物线y=-x2+bx+c与x轴交于A(1,0),B(-3,0)两点.
(1)求该抛物线的解析式;
解:(1)将点A,B代入抛物线,得
将①-②,得8+4b=0,
∴b=-2,
代入①,得c=1-b=3,
∴y=-x2-2x+3;
(2)设抛物线与y轴交于点C,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出点Q的坐标;若不存在,请说明理由;
如图1,由抛物线性质可知点A关于x=-1的对称点为B,
解:(2)令x=0,∴y=3,∴C(0,3),∴对称轴x=-1.
∴AQ+QC=BQ+QC≥BC(三角形两边之和大于第三边,Q在BC上时取等号)
∴△QAC周长最小时,Q为BC与x=-1的交点.
②代入①,得k=1,∴y=x+3.
令x=-1,得y=2,∴Q(-1,2);
设lBC:y=kx+b,代入B,C,得
(3)如图2,P是线段BC上的一个动点.过点P作y轴的平行线交抛物线于点E,求线段PE长度的最大值.
解:(3)设P(m,m+3)(-3≤m≤0),点P在线段BC上,
∴E(m,-m2-2m+3).
∵PE∥y轴,E在抛物线上,
∴PE=-m2-2m+3-(m+3)=-m2-3m
= ,
故PE最大值为 .
10. (2022·雁塔区四模)抛物线W:y=ax2+bx+3(a≠0)与x轴交于A(1,0),B(4,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
解:(1)∵y=ax2+bx+3(a≠0)与x轴交于A(1,0),B(4,0),
2 与等腰三角形,特殊四边形综合
∴ 解得
∴抛物线的解析式为y= x2- x+3;
(2)已知点P为x轴上一点,是否存在这样的点P,使得△BCP是以CP为腰的等腰三角形,若存在,请求出点P的坐标;若不存在,请说明理由.
∴点C(0,3).
设点P(x,0),由点C,B,P的坐标,得
CP2=x2+32,PB2=(x-4)2,CB2=42+32=25,
当PC=CB时,x2+32=25,解得x=4(舍去)或-4;
解:(2)∵抛物线的解析式为y= x2- x+3,
∴点P的坐标为 或(-4,0).
当PC=PB时,即x2+32=(x-4)2.解得x= ;
11.(2022·番禺区期中)如图,抛物线y=- x2+bx+c与x轴交于点A,B,与y轴交于点C.直线y=2x+2经过点A,C.
(1)抛物线的解析式为____________________,点B的坐标为______;
(4,0)
解:(1)对于y=2x+2,令y=2x+2=0,解得x=-1;
令x=0,则y=2,故点A,C的坐标分别为(-1,0),(0,2).
将点A,C的坐标代入抛物线表达式,得
解得x=4或-1,故点B(4,0).
解得
故抛物线的表达式为y=- x2+ x+2. ①
令y=- x2+ x+2=0,
故答案为y=- x2+ x+2,(4,0);
(2)若点P是第一象限内抛物线上一点,连接BP并延长交直线AC于点E,当CE=AC时,求点P的横坐标;
解:(2)由点A,B,C的坐标知,
AB=5,AC2=5,BC2=20,即AB2=AC2+BC2,
∴△ABC为直角三角形,即BC⊥AE.
而CE=AC,故AB=EB=5.
设点E(m,2m+2),则(m-4)2+(2m+2)2=25,
解得m=-1(舍去)或1,故点E(1,4).
由B,E的坐标,得直线BE的表达式为y=- x+ . ②
联立①②并解得x=4(舍去)或 ,
即点P的横坐标为 ;
(3)若点G是抛物线上一点,点H是x轴上一点,是否存在这样的点G,H,使以点A,C,G,H为顶点的四边形是平行四边形?若存在,请求出点G的坐标;若不存在,请说明理由.
当AC是平行四边形的对角线时,
由中点坐标公式,得0+2=n+0,解得n=2,
当AH是平行四边形的对角线时,
当AG是平行四边形的对角线时,同理可得,点G(3,2).
解:(3)存在.理由如下:设点G(m,n),n=- m2+ m+2.
即n=- m2+ m+2=2,解得m=0(舍去)或3,即点G(3,2);
同理可得0+0=n+2,解得n=-2,则点G ;
综上所述,点G的坐标为 或G(3,2).
12. 如图1,抛物线y=ax2+c与x轴交于点A,B,与y轴交于点C,P为x轴下方抛物线上一点,若OC=2OA=4.
(1)求抛物线解析式;
3 二次函数与角度
解:(1)∵OC=4,∴c=-4,
∴抛物线的解析式为y=ax2-4,
∵OC=2OA=4,∴A(-2,0),
∴0=4a-4,解得a=1,
∴抛物线的解析式为y=x2-4;
(2)如图2,若∠ABP=∠ACO,求点P的坐标.
解:(2)如图2,过点A作x轴的垂线交BP的延长线于点Q.
∴△BAQ≌△COA(ASA),∴AQ=OA=2,∴Q(-2,-2).
∵B(2,0),Q(-2,-2),
在△BAQ和△COA中,
∴直线BQ的解析式为y= x-1,
联立 解得 (舍去)或
∴点P坐标为 .
13.(2022·云安区模拟)如图,在平面直角坐标系中,已知抛物线y=-x2+bx+c与x轴交于A,B(4,0)两点,与y轴交于点C,点D(3,4)在抛物线上,点P是抛物线上一动点.
(1)求该抛物线的解析式;
解:(1)∵点B(4,0),
点D(3,4)在抛物线y=-x2+bx+c上,
∴该抛物线的解析式为y=-x2+3x+4;
∴
解得
(2)如图1,连接OD,若OP平分∠COD,求点P的坐标;
①当点P在第一象限时,作PE∥y轴,交OD于点Q,交x轴于点E.
解:(2)如图1,分两种情况讨论:
∵PE∥y轴,∴∠OPQ=∠POC.
∵OP平分∠COD,∴∠POC=∠POQ,
∴∠POQ=∠OPQ,∴PQ=OQ.
设点P的横坐标为t,则P(t,-t2+3t+4),
设OD的解析式为y=kx,将D(3,4)代入,得k= ,
∴OD的解析式为y= x.
②延长PO交抛物线于点P′,由图1可知,点P′也符合题意.
解得t1=2,t2=-2(舍去),∴t=2,
∴-t2+3t+4=-4+6+4=6,
∴点P的坐标为(2,6);
由点P(2,6)可得直线OP的解析式为y=3x.
Q ,E(t,0),其中0
∴OQ= = t.∴ t=-t2+ t+4,
∴点P′(-2,-6).
综上所述,点P的坐标是(2,6)或(-2,-6);
联立 解得
(3)如图2,连接AC,BC,抛物线上是否存在点P,使∠CBP+∠ACO=45°?若存在,请直接写出点P的坐标;若不存在,请说明理由.
解:(3)如图2,过点B作∠ABP=∠ACO,
交y轴正半轴于点F,交抛物线于点P,
则∠CBP+∠ACO=∠CBP+∠ABP=∠ABC=45°.
∵∠OBF=∠OCA,OB=OC,∠BOF=∠COA=90°,
∴△OBF≌△OCA,∴OF=OA=1,∴F(0,1).
设直线BF的解析式为y=mx+n,
将B(4,0),F(0,1)代入,得 解得
∴直线BF的解析式为y=- x+1,
由对称的性质,得∠F′CB=∠FCB=45°,
CF′=CF=OC-OF=3,∠CBF′=∠CBF.
∴点P′也符合题意.
∵∠F′CB=∠OBC=45°,
∴CF′∥OB,∴F′(3,4).
联立 解得 或 ∴P ;
如图2,作点F关于直线BC的对称点F′,作射线BF′交抛物线于点P′,
由点B(4,0)和点F′(3,4)可得直线BF′的解析式为
y=-4x+16,
∴点P′的坐标是(3,4).
联立 解得 或
综上所述,点P的坐标是 或(3,4).
4 求三角形面积最大值
14. 如图,抛物线y=x2+bx+c与x轴交于点A(-1,0),与y轴交于点C(0,-3).
(1)求该抛物线的解析式及顶点坐标;
解:(1)把点A(-1,0),点C(0,-3)代入抛物线的解析式得
∴抛物线的解析式为y=x2-2x-3,
∵y=x2-2x-3=(x-1)2-4,
∴顶点的坐标为(1,-4);
解得
(2)若P是线段OB上一动点,过P作y轴的平行线交抛物线于点H,交BC于点N,设OP=t,△BCH的面积为S,求S关于t的函数关系式.若S有最大值,请求出S的最大值;若没有,请说明理由.
解:(2)如图,设直线BC的解析式为y=kx+d(k≠0),
在抛物线上,当y=0时,即x2-2x-3=0,
解得:x1=3,x2=-1,∴B(3,0),
将B(3,0),C(0,-3)代入y=kx+d(k≠0)中,
∴直线BC的解析式为y=x-3,
∵OP=t,B(3,0),∴OB=3,
设点P的坐标为(t,0),
得 解得
则点N的坐标为(t,t-3),点H的坐标为(t,t2-2t-3),
∴NH=t-3-(t2-2t-3)=-t2+3t,
∴S=S△BCH=S△BNH+S△CNH= NH·OB= ×3(-t2+3t)
=- t2+ t=-
∵0≤t≤3,- <0,∴S有最大值,
∴当t= 时,S取最大值,最大值为 .
15. (2022·东营区模拟)如图,已知抛物线y=-x2+2x+3 与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,连接BC.
(1)求A,B,C三点的坐标;
解:(1)对于y=-x2+2x+3,
5 二次函数与直角三角形综合
令x=0,则y=3,∴C(0,3),
令y=0,则y=-x2+2x+3=0,
解得x1=3,x2=-1,
∴A(-1,0),B(3,0);
(2)若点P为线段BC上的一点(不与B,C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当线段PM的长度最大时,求点M的坐标;
解:(2)设BC的表达式为y=kx+b,
∴直线BC的表达式为y=-x+3.
设点P的坐标为(t,-t+3),
则点M的坐标为(t,-t2+2t+3),
则 解得
∴PM=-t2+2t+3+t-3=-t2+3t=- + ,
当t= 时,PM最大,此时点M的坐标为 ;
(3)在(2)的条件下,当线段PM的长度最大时,在抛物线的对称轴上有一点Q,使得△CNQ为直角三角形,直接写出点Q的坐标.
解:(3)∵y=-x2+2x+3=-(x-1)2+4,
∴抛物线的对称轴为直线x=1,
∵△CNQ为直角三角形,
∴分点C为直角顶点、点Q为直角顶点和点N为直角顶点三种情况:
∴设Q(1,m),且C(0,3),N ,
∴CN= ,CQ= ,
NQ= .
①当点C为直角顶点时,则有CN2+CQ2=NQ2,
②当点Q为直角顶点时,则有CQ2+NQ2=CN2,
即 +(m2-6m+10)=m2+ ,解得m= ,
此时点Q的坐标为 ;
即(m2-6m+10)+m2+ = ,
解得m1= ,m2= ,
③当点N为直角顶点时,则有CN2+NQ2=CQ2,
此时点Q的坐标为 或 ;
即 +m2+ =(m2-6m+10),
解得m=- ,此时点Q的坐标为 .
综上所述,点Q坐标为 或 或 或
.
同课章节目录
