统计(江苏省)范例与练习(练习无答案)
图片预览




文档简介
范例与练习
例题 \ 练习
例1 因为样本是总体的一部分,是由某些个体组成的,尽管对总体有一定的代表性,但毕竟不等于总体,为什么不把所有的个体考察一遍,使样本就是总体?
解 如果样本就是总体,抽样调查就变成了普查。尽管更真实可靠地反映了实际情况,但其可操作性、可行性、人力物力方面,都会有制约因素存在。何况有些调查是破坏性的,如一批玻璃的抗破碎能力、一批电池的使用寿命,普查就全报废了。因此,我们只能在条件许可的情况下,适当增加样本容量,并在取样过程中尽可能提高样本的代表性,去获取能客观地反映实际状况的样本数据,再对这些数据进行整理、计算、分析,作出科学的估计,这正是统计的基本思想。
评析 本例涉及总体,个体,样本,样本的容量等基本知识,有助于我们进一步体会统计的基本思想,掌握将统计知识应用于实际问题的基本技能。
例2 某校组织高三年级800名学生参加高考模拟考,其中理科类考生560人,文科类考生240人,为了调研数学学科有关教学情况,打算抽取一个容量为40的样本,问此样本该如何获得,写出抽样过程。
解 因为不同科类的学生参加考试的数学试卷不同,故应先采用分层抽样的方法,由于560:240=7:3,设两类学生各抽个体数分别为,,由+=40,得=4,故理科类考生应抽28人,文科类考生应抽12人。
考虑到理科类考生人数较多,可采用系统抽样的方法获得样本:首先,将该校所有560名理科类考生用随机方式编号(如按学号顺序),000,001,002,…,559,第2步,按编号顺序分成28段,每段20人,在第一段000,001,002, …,019这20个编号中,随机定一起始号则编号…,为所抽取的理科类考生的一个样本。
又考虑到文科类考生人数较少,可采用简单随机抽样方法获得样本:首先,将该校所有240名文科类考生都编上号码:001,002,003,…,240,如用抽签法,则做240个形状、大小相同的号签,然后将这些号签放在同一个箱子里,进行均匀搅拌。抽签时,每次从中抽出一个号签,连续抽12次,就得到一个容量为12的样本。如用随机数表法,则可在数表上随机选定一个起始位置,如起始位置是表中第7行17列的数字0,从0开始向右连续取数字,以三个数为一组,碰到右边线时向下错一行向左继续取,所得数字如下:068,877,047,447,672,176,335,025,839,212,067,697,832,…,所取录的三位数字如果不大于240,则对应此号的学生就是被抽取的个体,如果所取录的三位数字大于240而不大于480,则减去240,剩余数即是被抽取的号码,如果大于480而不大于720,则减去480,依此类推,如果遇到相同的号码,则只留第一次录取的数字,其余的舍去,经过这样处理,被抽取的学生对应号码分别是068,157,047,207,192,176,95,025,119,212,067,217,这样就得到文科类考生的一个样本。
综上,我们就得到一个容量为40的样本。
评析 本例中基本知识有:简单随机抽样,系统抽样,分层抽样的意义及三种抽样方法的联系与适用范围。通过对三种抽样方法的具体操作,培养科学、求实的学习、工作态度,保证抽样的公平性、客观性、准确性和可信性,体会每个个体等可能入样的随机抽样基本思想。
例3 某盐场有甲、乙两套设备包装食盐,在自动包装传送带上,每隔3分钟抽一包称其重量是否合格,分别记录数据如下:
甲套设备:504,510,505,490,485,485,515,510,496,500;
乙套设备:496,502,501,499,505,498,499,498,497,505.
(1) 试确定这是何种抽样方法?
(2) 比较甲、乙两套设备的平均值与方差,说明哪套包装设备误差较少?
解 (1)根据系统抽样方法的定义,可知这种抽样方法是系统抽样。
(2)甲套设备的平均值、方差分别为
;
…;
乙套设备的平均值、方差分别为
;
…;
可见,,所以乙套设备较甲套设备更稳定,误差较少。
评析 本例中基础知识包括抽样方法、数据的平均值与方差及其实际意义。要求掌握抽样方法的确定、数据的平均值与方差的计算、抽样方法在实际问题中的应用等基本技能,培养用样本估计总体的统计基本思想和数学建模的思想。
例4 为了解某校初中毕业班男生的身体发育情况,用随机抽样的方法抽查了100名同一年龄组学生的身高资料如下(单位:cm):
165.5 166.5 165 161.5 164.5 164.5 166 164.5 176 158.5
170 173.5 156 163 172 157.5 165.5 168 171 175
166 168.5 162.5 162 159.5 163.5 164.5 167.5 173 168
155 172 166.5 174 163 160 168 166.5 164.5 158
164 170.5 165 162.5 157 169 171.5 173 162 158
171.5 158 166 163.5 162 159.5 164 165 170 174.5
168.5 164 155.5 172.5 66.5 168 176 165.5 160 171
164 169.5 174 164.5 159 161.5 167 155.5 163.5 176
159 165.5 162.5 169.5 172 169.5 175.5 168.5 157 156
156.5 158.5 167.5 170.5 167 163.5 170 170 165 159.5
试根据上述数据画出样本的频率分布直方图,并对相应的总体分布作出估计。
解 可按照下列步骤获得样本的频率分布。
(1) 计算最大值与最小值的差(极差):
在样本数据中,最大值是176,最小值是155,它们的极差是176-155=21(cm).
(2) 确定组距与组数:
如果将组距定为2cm,那么由21÷2=10.5,组数为11,这个组数是合适的,于是取定组距为2cm,组数为11。
(3)决定分点:
根据上述数据的特点,第1小组的起点可取为154.5,第1小组的终点可取为156.5,为了避免一个数据既是起点,又是终点从而造成重复计算,不妨规定分组的区间是“左闭右开”的。这样,所得到的分组是
,,…,
(3) 列出频率分布表,如下表:
分组 频数 频率
2 0.02
5 0.05
10 0.10
10 0.10
14 0.14
17 0.17
13 0.13
11 0.11
8 0.08
7 0.07
3 0.03
合计 100 1.00
(5)画出频率分布直方图:
在得到了样本的频率分布后,就可以对相应的总体情况作出估计。例如可以估计,身高在164.5~166.5cm的学生最多,约占学生总数的17%,身高低于158.5cm的学生约占7%,身高超过174.5 cm的学生较少,仅占3%等 。
评析 本例中基础知识有:样本数据,总体分布的估计,频率分布表,频率分布直方图及其相互联系;基本技能:频率分布表、频率分布直方图的操作步骤,用频率分布表、频率分布直方图估计总体分布;其基本数学思想有:对不同元素进行重组、分类讨论的思想方法。
例5 (1)设一组数据…,的平均数为,方差为.
求证:….
(2)设,,…,,记….
求证:….
证明 (1)…
……
….
(2)∵,∴,
同理 ,…,,
∴ …
…
….
评析 这个结论告诉我们,将一组数据中每一个数减去同一个数,方差不变。因此,当样本数据较大时,如果数据相互比较接近,我们不妨将每个数据减去一个与样本平均数接近的常数,再计算方差。这样处理,可在样本方差计算中有效地减少运算量,深入体会利用已知公式、结论进行转换的等价转化思想和整体处理的思想,灵活掌握样本平均数、样本方差等基础知识。
例6 下表是某医院用光电比色计检验尿汞时,得到的尿汞含量(毫克/升)与消光系数的一组数据:
尿汞含量 2 4 6 8 10
消光系数 64 138 205 285 360
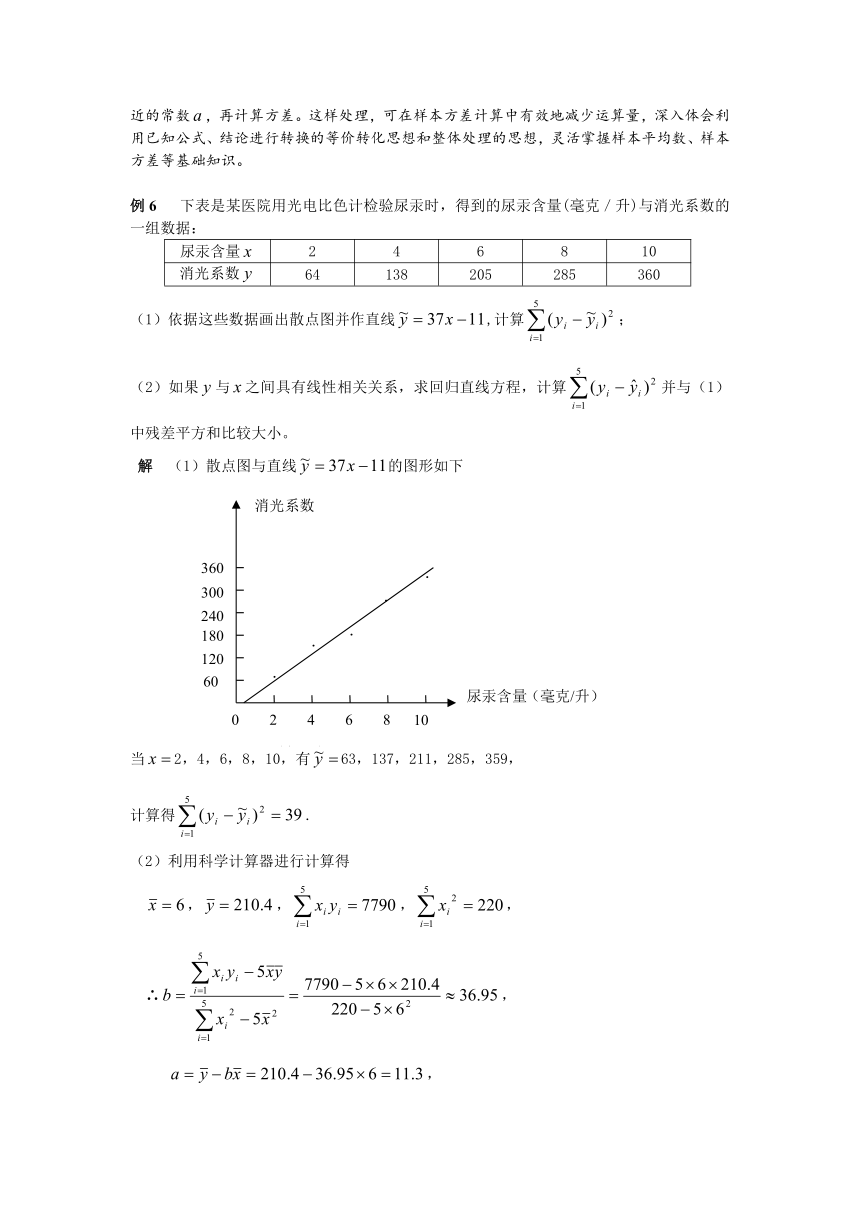
(1)依据这些数据画出散点图并作直线,计算;
(2)如果与之间具有线性相关关系,求回归直线方程,计算并与(1)中残差平方和比较大小。
解 (1)散点图与直线的图形如下
当2,4,6,8,10,有63,137,211,285,359,
计算得.
(2)利用科学计算器进行计算得
,,,,
∴,
,
故所求回归直线方程为,
且有62.6,136.5,210.4,284.3,358.2,计算得,
比较可知用最小二乘法求出的残差平方和较小。
评析 本例包含数形结合、线性回归、最小二乘法等基本数学思想,涉及线性回归分析、散点图、回归直线等基础知识及作两个变量的一组数据的散点图、利用计算器或计算机求回归直线方程等基本技能。
一、选择题
1.为了解学生佩戴校徽的真实情况,值日小组在学校某一路段随机抽查,这种抽查是( ).
(A)简单随机抽样 (B)分层抽样 (C)不放回抽样 (D)有放回抽样
2.若某项改革方案与不同职业的人员有关系,为了抽查对这一方案的支持率,你认为最合适的抽样方法是( ).
(A)分层抽样 (B)抽签法 (C)随机数表法 (D)有放回抽样
3.一个学校有初中生800人,高中生1200人,则是初中生占全体学生的( ).
(A)频数 (B)频率 (C)概率 (D)频率分布
4.以下哪一个数不是总体的特征数( ) .
(A)总体平均数 (B)总体方差 (C)总体标准差 (D)总体的样本
5.光明中学高一年级360名学生选择摄影、棋类、
武术、美术四门校本课程情况的扇形统计图如右,
从图中可以看出选择美术的学生人数是( ).
(A)18 (B)24
(C)36 (D)54
6.一组数据按大小关系排列为1,2,4,,6,9.这组数据的中位数为5,那么这组数据的众数为( ).
(A)4 (B)5 (C)5.5 (D)6
7.用简单随机抽样的方法从含有个个体的总体中抽取一个样本,则在抽样过程中,每个个体被抽取的可能性( ).
(A)相等 (B)逐渐增大 (C)逐渐减少 (D)不能确定
8.将一组数据…改变为…,其中,则下列结论正确的是( ).
(A)平均数与方差均不变 (B)平均数不变,方差改变
(C)平均数改变,方差不变 (D)平均数、方差都改变
9.设有一个回归方程,则变量增加一个单位时,下列结论正确的是( ).
(A) 平均增加1.5个单位 (B) 平均增加2个单位
(C) 平均减少1.5个单位 (D) 平均减少2个单位
10.高二(1)班某次数学考试的平均分为70分,标准差为,后来发现成绩记录有误,某甲得80分却误记为60分,某乙得70分却误记为90分,更正后计算得标准差为,则和之间的大小关系是( ).
(A) (B) (C) (D)与人数有关,无法判断
二、填空题
11.在统计中,经常从总体中抽取一个样本,用样本的 去估计总体的分布,样本的 ,这种估计也越准确。
12.某校高三、高二、高一三个年级的学生数分别为600人、650人、700人,现采用按年级分层抽样方法了解学生的视力状况,如果在高一年级共抽查了28人,那么这次抽查的容量 人。
13.在表示频率分布的直方图中,小长方形的面积等于 。
14.一个容量为20的样本数据分组后,各组与频数如下:
,3;,5;,5;,4;,2;,1.
则样本在上的频率为 。
15.某市对家庭购买轿车进行调查,共抽查3258个家庭,有586户购买了轿车,则该市家庭购买轿车购买率估计是 。
16.为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,结果用以下的条形图表示,根据条形图可得这50名学生这一天平均每人的课外阅读时间为 小时.
17.在抽查某产品尺寸的过程中,将其尺寸分成若干组,是其中一组,若该组上的直方图的高为,那么该组的频率等于 。
18.学校阶梯教室共20排,每排有18个座位,一次讲座时坐满了学生,会后为了了解有关情况留下了所有座位号是10号的20位学生测试,这里运用的抽样方法是 。
19.某校高二年级有4个理科班,各班的人数分别是52、54、54、53,各班的数学平均分分别是81、80、82、83,则这四个班的平均分是 (精确到0.1)。
20.有人用回归方程(磅/英寸)(磅)由身高预测体重,其中体重与身高分别以磅和英寸为单位,已知1英寸2.5cm,1磅0.45kg,那么当小王的身高达到1.75m时,体重约为 kg.
21.随机抽查某校2006年10月份某星期5天中每天的用电量,数据如下:294,305,285,306,310,已知2006年10月1日是星期天,国家规定国庆节放假3天,若遇星期六、星期天可以补休,假定双休、节假日学校不用电,请你估计该校10份的总电量约为 度.
22.右图是200辆汽车经过某一
雷达测速区的时速频率分布直方
图,则时速超过60km/h的汽车
大约有 辆.
三、解答题
23.一个城市有240家商店,其中大型商店有36家,中型有60家,小型有144家,为掌握各商店的营业情况,要从中抽取一个容量为21的样本,你认为应该按照哪种抽样方法抽取样本?各类商店要抽多少家?写出抽样过程.
24.在某旅游景区上山的一条小路上,有一些断断续续的台阶.其中的甲、乙段台阶路的示意图如右所示.请你用所学过的有关统计的
数字特征(平均数、众数、中位数、方差和
极差)回答下列问题:
(1)两段台阶路有哪些相同点和不同点?
(2)哪段台阶路走起来更舒服?为什么?
(3)为方便游客行走,需要重新整修上山的小路.对于这两段台阶路,在台阶数不变的情况下,请你提出合理的整修建议.
25.为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图如图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,求各组的最大频率和视力在4.6到5.0之间的学生数。
26.为检查甲、乙两厂的100瓦灯泡的生产质量,分别从生产机器的传送带上每隔30分钟取一只,各抽取了20只灯泡,结果如下:
瓦 94 96 98 100 102 104 106
甲厂个数 0 3 6 8 2 0 1
乙厂个数 1 2 7 4 3 2 1
(1) 试估计甲、乙两厂灯泡瓦数的平均值;
(2) 如果在95~105瓦范围内的灯泡为合格品.计算两厂合格品的比例分别是多少;
(3) 哪个厂的生产情况比较稳定?
27.中学生的心理健康问题已引起了社会的广泛关注,黎明中学对全校600名学生进行了一次“心理健康”知识测试,并从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
分 组 频数 频率
50.5~60.5 2 0.04
60.5~70.5 0.16
70.5~80.5 10
80.5~90.5
90.5~100.5 0.28
合 计 1.00
请填写频率分布表中的空格,并补全频率分布直方图.
28.某中学高二年级共有600名学生,现抽查60名同学的数学测试成绩如下:
92 88 76 91 68 94 35 58 81 72
69 75 96 81 85 80 62 77 73 64
87 68 64 49 52 97 76 58 78 91
63 87 89 71 90 74 69 88 65 49
83 74 69 64 66 78 98 86 53 60
79 80 63 65 47 95 43 84 72 61
(1) 列出频率分布表;
(2) 画出频率分布直方图;
(3) 估计不及格和优秀(80分及以上)的人数.
29.在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交作品的件数按照5天一组分组统计,绘制了频率分布直方图(如图),已知从左到右各长方形的高的比为2∶3∶4∶6∶4∶1,第三组的频数为12,请解答下列各题:
(1) 本次活动共有多少件作品参加评比?
(2) 哪组上交的作品数量最多?有多少件?
(3) 经过评比,第四组和第六组分别有10件,2件作品获奖,问这两组哪一组获奖率较高?
30.奥林匹克运动体现了人类挑战自我的精神,以下数据给出了到2001年为止的现代奥林匹克运动会的男子最好赛跑成绩:
距离(单位:m) 100 200 400 800 1500 5000 10000
时间(单位:s) 9.84 19.32 43.49 103 213 786 1627
(1) 用以上数据作出时间关于距离的散点图;
(2) 如果时间与距离具有显著线性相关,试根据散点图判断它们是正相关还是负相关,并求时间关于距离的一元线性回归方程.
0.025
154.5 156.5 158.5 160.5 162.5 164.5 166.5 168.5 170.5 172.5 174.5 176.5
0
频率/组距
身高
例题
0.050
0.075
0.100
120
240
尿汞含量(毫克/升)
2
4
6
8
10
0
消光系数
360
300
180
60
.
.
.
.
.
练习
美
术
武术
30%
摄影
25%
棋类
40%
时间(小时)
人数
0 0.5 1.0 1.5 2.0
20
15
10
5
0.010
0.028
0.005
0.018
0.039
30 40 50 60 70 80 时速(km/h)
频率/组距
11
10
15
18
17
19
乙段
16
14
15
16
14
15
甲段
频率/组距
视力
0.1
0.3
4.3 4.4 4.5 4.6 4.7 4.8 4.9 5.0 5.1 5.2
频率/组距
成绩(分)
50.5 60.5 70.5 80.5 90.5 100.5
0.004
日期
频率/组距
例题 \ 练习
例1 因为样本是总体的一部分,是由某些个体组成的,尽管对总体有一定的代表性,但毕竟不等于总体,为什么不把所有的个体考察一遍,使样本就是总体?
解 如果样本就是总体,抽样调查就变成了普查。尽管更真实可靠地反映了实际情况,但其可操作性、可行性、人力物力方面,都会有制约因素存在。何况有些调查是破坏性的,如一批玻璃的抗破碎能力、一批电池的使用寿命,普查就全报废了。因此,我们只能在条件许可的情况下,适当增加样本容量,并在取样过程中尽可能提高样本的代表性,去获取能客观地反映实际状况的样本数据,再对这些数据进行整理、计算、分析,作出科学的估计,这正是统计的基本思想。
评析 本例涉及总体,个体,样本,样本的容量等基本知识,有助于我们进一步体会统计的基本思想,掌握将统计知识应用于实际问题的基本技能。
例2 某校组织高三年级800名学生参加高考模拟考,其中理科类考生560人,文科类考生240人,为了调研数学学科有关教学情况,打算抽取一个容量为40的样本,问此样本该如何获得,写出抽样过程。
解 因为不同科类的学生参加考试的数学试卷不同,故应先采用分层抽样的方法,由于560:240=7:3,设两类学生各抽个体数分别为,,由+=40,得=4,故理科类考生应抽28人,文科类考生应抽12人。
考虑到理科类考生人数较多,可采用系统抽样的方法获得样本:首先,将该校所有560名理科类考生用随机方式编号(如按学号顺序),000,001,002,…,559,第2步,按编号顺序分成28段,每段20人,在第一段000,001,002, …,019这20个编号中,随机定一起始号则编号…,为所抽取的理科类考生的一个样本。
又考虑到文科类考生人数较少,可采用简单随机抽样方法获得样本:首先,将该校所有240名文科类考生都编上号码:001,002,003,…,240,如用抽签法,则做240个形状、大小相同的号签,然后将这些号签放在同一个箱子里,进行均匀搅拌。抽签时,每次从中抽出一个号签,连续抽12次,就得到一个容量为12的样本。如用随机数表法,则可在数表上随机选定一个起始位置,如起始位置是表中第7行17列的数字0,从0开始向右连续取数字,以三个数为一组,碰到右边线时向下错一行向左继续取,所得数字如下:068,877,047,447,672,176,335,025,839,212,067,697,832,…,所取录的三位数字如果不大于240,则对应此号的学生就是被抽取的个体,如果所取录的三位数字大于240而不大于480,则减去240,剩余数即是被抽取的号码,如果大于480而不大于720,则减去480,依此类推,如果遇到相同的号码,则只留第一次录取的数字,其余的舍去,经过这样处理,被抽取的学生对应号码分别是068,157,047,207,192,176,95,025,119,212,067,217,这样就得到文科类考生的一个样本。
综上,我们就得到一个容量为40的样本。
评析 本例中基本知识有:简单随机抽样,系统抽样,分层抽样的意义及三种抽样方法的联系与适用范围。通过对三种抽样方法的具体操作,培养科学、求实的学习、工作态度,保证抽样的公平性、客观性、准确性和可信性,体会每个个体等可能入样的随机抽样基本思想。
例3 某盐场有甲、乙两套设备包装食盐,在自动包装传送带上,每隔3分钟抽一包称其重量是否合格,分别记录数据如下:
甲套设备:504,510,505,490,485,485,515,510,496,500;
乙套设备:496,502,501,499,505,498,499,498,497,505.
(1) 试确定这是何种抽样方法?
(2) 比较甲、乙两套设备的平均值与方差,说明哪套包装设备误差较少?
解 (1)根据系统抽样方法的定义,可知这种抽样方法是系统抽样。
(2)甲套设备的平均值、方差分别为
;
…;
乙套设备的平均值、方差分别为
;
…;
可见,,所以乙套设备较甲套设备更稳定,误差较少。
评析 本例中基础知识包括抽样方法、数据的平均值与方差及其实际意义。要求掌握抽样方法的确定、数据的平均值与方差的计算、抽样方法在实际问题中的应用等基本技能,培养用样本估计总体的统计基本思想和数学建模的思想。
例4 为了解某校初中毕业班男生的身体发育情况,用随机抽样的方法抽查了100名同一年龄组学生的身高资料如下(单位:cm):
165.5 166.5 165 161.5 164.5 164.5 166 164.5 176 158.5
170 173.5 156 163 172 157.5 165.5 168 171 175
166 168.5 162.5 162 159.5 163.5 164.5 167.5 173 168
155 172 166.5 174 163 160 168 166.5 164.5 158
164 170.5 165 162.5 157 169 171.5 173 162 158
171.5 158 166 163.5 162 159.5 164 165 170 174.5
168.5 164 155.5 172.5 66.5 168 176 165.5 160 171
164 169.5 174 164.5 159 161.5 167 155.5 163.5 176
159 165.5 162.5 169.5 172 169.5 175.5 168.5 157 156
156.5 158.5 167.5 170.5 167 163.5 170 170 165 159.5
试根据上述数据画出样本的频率分布直方图,并对相应的总体分布作出估计。
解 可按照下列步骤获得样本的频率分布。
(1) 计算最大值与最小值的差(极差):
在样本数据中,最大值是176,最小值是155,它们的极差是176-155=21(cm).
(2) 确定组距与组数:
如果将组距定为2cm,那么由21÷2=10.5,组数为11,这个组数是合适的,于是取定组距为2cm,组数为11。
(3)决定分点:
根据上述数据的特点,第1小组的起点可取为154.5,第1小组的终点可取为156.5,为了避免一个数据既是起点,又是终点从而造成重复计算,不妨规定分组的区间是“左闭右开”的。这样,所得到的分组是
,,…,
(3) 列出频率分布表,如下表:
分组 频数 频率
2 0.02
5 0.05
10 0.10
10 0.10
14 0.14
17 0.17
13 0.13
11 0.11
8 0.08
7 0.07
3 0.03
合计 100 1.00
(5)画出频率分布直方图:
在得到了样本的频率分布后,就可以对相应的总体情况作出估计。例如可以估计,身高在164.5~166.5cm的学生最多,约占学生总数的17%,身高低于158.5cm的学生约占7%,身高超过174.5 cm的学生较少,仅占3%等 。
评析 本例中基础知识有:样本数据,总体分布的估计,频率分布表,频率分布直方图及其相互联系;基本技能:频率分布表、频率分布直方图的操作步骤,用频率分布表、频率分布直方图估计总体分布;其基本数学思想有:对不同元素进行重组、分类讨论的思想方法。
例5 (1)设一组数据…,的平均数为,方差为.
求证:….
(2)设,,…,,记….
求证:….
证明 (1)…
……
….
(2)∵,∴,
同理 ,…,,
∴ …
…
….
评析 这个结论告诉我们,将一组数据中每一个数减去同一个数,方差不变。因此,当样本数据较大时,如果数据相互比较接近,我们不妨将每个数据减去一个与样本平均数接近的常数,再计算方差。这样处理,可在样本方差计算中有效地减少运算量,深入体会利用已知公式、结论进行转换的等价转化思想和整体处理的思想,灵活掌握样本平均数、样本方差等基础知识。
例6 下表是某医院用光电比色计检验尿汞时,得到的尿汞含量(毫克/升)与消光系数的一组数据:
尿汞含量 2 4 6 8 10
消光系数 64 138 205 285 360
(1)依据这些数据画出散点图并作直线,计算;
(2)如果与之间具有线性相关关系,求回归直线方程,计算并与(1)中残差平方和比较大小。
解 (1)散点图与直线的图形如下
当2,4,6,8,10,有63,137,211,285,359,
计算得.
(2)利用科学计算器进行计算得
,,,,
∴,
,
故所求回归直线方程为,
且有62.6,136.5,210.4,284.3,358.2,计算得,
比较可知用最小二乘法求出的残差平方和较小。
评析 本例包含数形结合、线性回归、最小二乘法等基本数学思想,涉及线性回归分析、散点图、回归直线等基础知识及作两个变量的一组数据的散点图、利用计算器或计算机求回归直线方程等基本技能。
一、选择题
1.为了解学生佩戴校徽的真实情况,值日小组在学校某一路段随机抽查,这种抽查是( ).
(A)简单随机抽样 (B)分层抽样 (C)不放回抽样 (D)有放回抽样
2.若某项改革方案与不同职业的人员有关系,为了抽查对这一方案的支持率,你认为最合适的抽样方法是( ).
(A)分层抽样 (B)抽签法 (C)随机数表法 (D)有放回抽样
3.一个学校有初中生800人,高中生1200人,则是初中生占全体学生的( ).
(A)频数 (B)频率 (C)概率 (D)频率分布
4.以下哪一个数不是总体的特征数( ) .
(A)总体平均数 (B)总体方差 (C)总体标准差 (D)总体的样本
5.光明中学高一年级360名学生选择摄影、棋类、
武术、美术四门校本课程情况的扇形统计图如右,
从图中可以看出选择美术的学生人数是( ).
(A)18 (B)24
(C)36 (D)54
6.一组数据按大小关系排列为1,2,4,,6,9.这组数据的中位数为5,那么这组数据的众数为( ).
(A)4 (B)5 (C)5.5 (D)6
7.用简单随机抽样的方法从含有个个体的总体中抽取一个样本,则在抽样过程中,每个个体被抽取的可能性( ).
(A)相等 (B)逐渐增大 (C)逐渐减少 (D)不能确定
8.将一组数据…改变为…,其中,则下列结论正确的是( ).
(A)平均数与方差均不变 (B)平均数不变,方差改变
(C)平均数改变,方差不变 (D)平均数、方差都改变
9.设有一个回归方程,则变量增加一个单位时,下列结论正确的是( ).
(A) 平均增加1.5个单位 (B) 平均增加2个单位
(C) 平均减少1.5个单位 (D) 平均减少2个单位
10.高二(1)班某次数学考试的平均分为70分,标准差为,后来发现成绩记录有误,某甲得80分却误记为60分,某乙得70分却误记为90分,更正后计算得标准差为,则和之间的大小关系是( ).
(A) (B) (C) (D)与人数有关,无法判断
二、填空题
11.在统计中,经常从总体中抽取一个样本,用样本的 去估计总体的分布,样本的 ,这种估计也越准确。
12.某校高三、高二、高一三个年级的学生数分别为600人、650人、700人,现采用按年级分层抽样方法了解学生的视力状况,如果在高一年级共抽查了28人,那么这次抽查的容量 人。
13.在表示频率分布的直方图中,小长方形的面积等于 。
14.一个容量为20的样本数据分组后,各组与频数如下:
,3;,5;,5;,4;,2;,1.
则样本在上的频率为 。
15.某市对家庭购买轿车进行调查,共抽查3258个家庭,有586户购买了轿车,则该市家庭购买轿车购买率估计是 。
16.为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,结果用以下的条形图表示,根据条形图可得这50名学生这一天平均每人的课外阅读时间为 小时.
17.在抽查某产品尺寸的过程中,将其尺寸分成若干组,是其中一组,若该组上的直方图的高为,那么该组的频率等于 。
18.学校阶梯教室共20排,每排有18个座位,一次讲座时坐满了学生,会后为了了解有关情况留下了所有座位号是10号的20位学生测试,这里运用的抽样方法是 。
19.某校高二年级有4个理科班,各班的人数分别是52、54、54、53,各班的数学平均分分别是81、80、82、83,则这四个班的平均分是 (精确到0.1)。
20.有人用回归方程(磅/英寸)(磅)由身高预测体重,其中体重与身高分别以磅和英寸为单位,已知1英寸2.5cm,1磅0.45kg,那么当小王的身高达到1.75m时,体重约为 kg.
21.随机抽查某校2006年10月份某星期5天中每天的用电量,数据如下:294,305,285,306,310,已知2006年10月1日是星期天,国家规定国庆节放假3天,若遇星期六、星期天可以补休,假定双休、节假日学校不用电,请你估计该校10份的总电量约为 度.
22.右图是200辆汽车经过某一
雷达测速区的时速频率分布直方
图,则时速超过60km/h的汽车
大约有 辆.
三、解答题
23.一个城市有240家商店,其中大型商店有36家,中型有60家,小型有144家,为掌握各商店的营业情况,要从中抽取一个容量为21的样本,你认为应该按照哪种抽样方法抽取样本?各类商店要抽多少家?写出抽样过程.
24.在某旅游景区上山的一条小路上,有一些断断续续的台阶.其中的甲、乙段台阶路的示意图如右所示.请你用所学过的有关统计的
数字特征(平均数、众数、中位数、方差和
极差)回答下列问题:
(1)两段台阶路有哪些相同点和不同点?
(2)哪段台阶路走起来更舒服?为什么?
(3)为方便游客行走,需要重新整修上山的小路.对于这两段台阶路,在台阶数不变的情况下,请你提出合理的整修建议.
25.为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图如图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,求各组的最大频率和视力在4.6到5.0之间的学生数。
26.为检查甲、乙两厂的100瓦灯泡的生产质量,分别从生产机器的传送带上每隔30分钟取一只,各抽取了20只灯泡,结果如下:
瓦 94 96 98 100 102 104 106
甲厂个数 0 3 6 8 2 0 1
乙厂个数 1 2 7 4 3 2 1
(1) 试估计甲、乙两厂灯泡瓦数的平均值;
(2) 如果在95~105瓦范围内的灯泡为合格品.计算两厂合格品的比例分别是多少;
(3) 哪个厂的生产情况比较稳定?
27.中学生的心理健康问题已引起了社会的广泛关注,黎明中学对全校600名学生进行了一次“心理健康”知识测试,并从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
分 组 频数 频率
50.5~60.5 2 0.04
60.5~70.5 0.16
70.5~80.5 10
80.5~90.5
90.5~100.5 0.28
合 计 1.00
请填写频率分布表中的空格,并补全频率分布直方图.
28.某中学高二年级共有600名学生,现抽查60名同学的数学测试成绩如下:
92 88 76 91 68 94 35 58 81 72
69 75 96 81 85 80 62 77 73 64
87 68 64 49 52 97 76 58 78 91
63 87 89 71 90 74 69 88 65 49
83 74 69 64 66 78 98 86 53 60
79 80 63 65 47 95 43 84 72 61
(1) 列出频率分布表;
(2) 画出频率分布直方图;
(3) 估计不及格和优秀(80分及以上)的人数.
29.在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交作品的件数按照5天一组分组统计,绘制了频率分布直方图(如图),已知从左到右各长方形的高的比为2∶3∶4∶6∶4∶1,第三组的频数为12,请解答下列各题:
(1) 本次活动共有多少件作品参加评比?
(2) 哪组上交的作品数量最多?有多少件?
(3) 经过评比,第四组和第六组分别有10件,2件作品获奖,问这两组哪一组获奖率较高?
30.奥林匹克运动体现了人类挑战自我的精神,以下数据给出了到2001年为止的现代奥林匹克运动会的男子最好赛跑成绩:
距离(单位:m) 100 200 400 800 1500 5000 10000
时间(单位:s) 9.84 19.32 43.49 103 213 786 1627
(1) 用以上数据作出时间关于距离的散点图;
(2) 如果时间与距离具有显著线性相关,试根据散点图判断它们是正相关还是负相关,并求时间关于距离的一元线性回归方程.
0.025
154.5 156.5 158.5 160.5 162.5 164.5 166.5 168.5 170.5 172.5 174.5 176.5
0
频率/组距
身高
例题
0.050
0.075
0.100
120
240
尿汞含量(毫克/升)
2
4
6
8
10
0
消光系数
360
300
180
60
.
.
.
.
.
练习
美
术
武术
30%
摄影
25%
棋类
40%
时间(小时)
人数
0 0.5 1.0 1.5 2.0
20
15
10
5
0.010
0.028
0.005
0.018
0.039
30 40 50 60 70 80 时速(km/h)
频率/组距
11
10
15
18
17
19
乙段
16
14
15
16
14
15
甲段
频率/组距
视力
0.1
0.3
4.3 4.4 4.5 4.6 4.7 4.8 4.9 5.0 5.1 5.2
频率/组距
成绩(分)
50.5 60.5 70.5 80.5 90.5 100.5
0.004
日期
频率/组距
