3.1.2用二分法求方程的近似解
文档属性
| 名称 | 3.1.2用二分法求方程的近似解 |

|
|
| 格式 | rar | ||
| 文件大小 | 141.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-12-20 00:00:00 | ||
图片预览





文档简介
课件15张PPT。3.1.2用二分法求
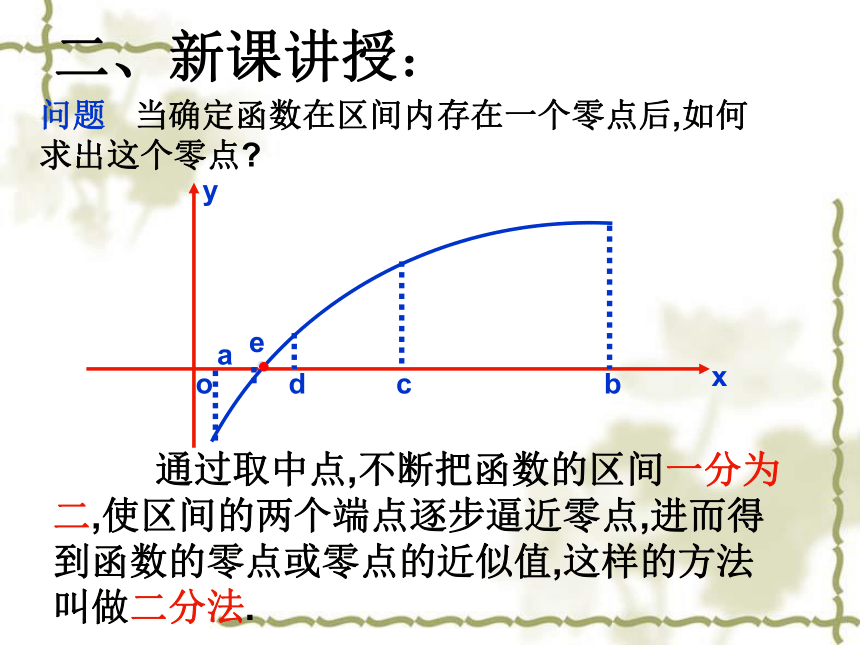
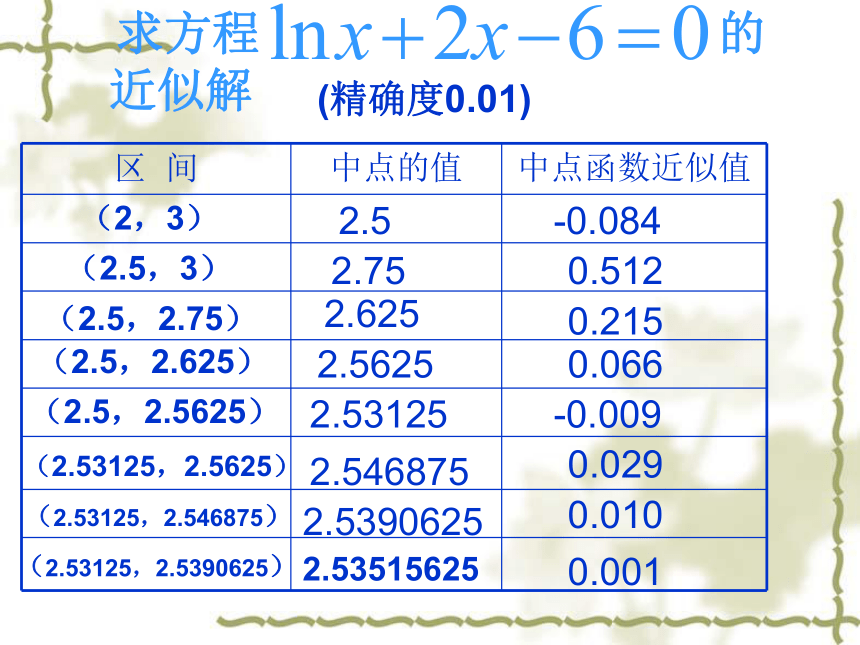
方程的近似解一、复习思考:1.函数的零点2.零点存在的判定使f(x)=0的实数x叫做函数y=f(x)的零点问题 当确定函数在区间内存在一个零点后,如何求出这个零点? 通过取中点,不断把函数的区间一分为二,使区间的两个端点逐步逼近零点,进而得到函数的零点或零点的近似值,这样的方法叫做二分法.cde二、新课讲授:例1 求函数f(x)=x3-3x2+2x-6在区间[0,4]内的零点.解 f(0)=-6<0 f(4)=18>0端点(中点)坐标中点的函数值取区间[0,4][2,4]X1=(0+4)/2=2X2=(2+4)/2=3f(x1)=f(2)=-6<0f(x2)=f(3)=0由上式计算可知,x2=3就是所求函数的一个零点.例1 求函数f(x)=lnx+2x-6的零点个数例2(补) 求函数f(x)=lnx+2x-6的零点(即求方程lnx+2x-6=0的实数根,精确到0.01)新课——把例1改写:2.52.752.6252.56252.531252.5468752.53906252.53515625-0.0840.5120.2150.066-0.0090.0290.0100.001(精确度0.01)(2,3)求方程的近似解
(2.5,3)(2.5,2.75)(2.5,2.625)(2.5,2.5625)(2.53125,2.5625) (2.53125,2.546875) (2.53125,2.5390625) 给定精确度,用二分法求函数零点x0的步骤: 1:确定初始区间[a,b],验证f(a)f(b)<0
2:求区间[a,b]的中点x1=
3:计算:f(x1)判断:
(1)如果f(x1)=0,则x1就是f(x)的零点,计算终止;
(2)如果f(a)f(x1)<0,则令b=x1 (此时零点x0∈(a,x1)中)
(3)如果f(a)f(x1)>0,则令a=x1(此时零点x0∈(x1,b)中)
4:判断是否达到精确度ε:若达到,则得到零点近似值是(a,b)区间内的一点;否则重复2~4步骤。 流程图即:找一个初始区间初始区间长度尽量小,一般通过作图来控制其区间长度↓计算区间中点的函数值是否为0↓是结束运算↓否找出新的端点异号区间是否满足精确度↓↓是→否例题:利用计算器,求方程2x=4-x的近似解 (精确到0.1)怎样找到它的解所在的区间呢?在同一坐标系内画函数y=2x
与y=4-x的图象,如图:提问:能否不画图确定根所在的区间?得:方程有一个解x0 ∈(0,4)如果画得很准确,可得x0 ∈(1,2)数学运用三、练习巩固:练习1:选择题
(1).下列函数的图象与x轴均有交点,其中不能用二分法求其零点的是 ( )C问题:根据练习1,请思考利用二分法求函数
零点的条件是什么? 1、函数y=f (x)在[a,b]上连续不断。2、 y=f (x)满足 f (a)f (b)<0,则在(a,b)内必有零点(2). 方程lnx+2x=6在区间上的根必定属于区间( )
?(A)(-2,1) (B)( ,4)
(C) (1, ) (D) ( , )
??(3).下列函数图像与x轴均有交点,但不宜用二分法求交点横坐标的是( )ABCDBB练习2:
求方程x3+3x-1=0的一个近似解(精确到 0.01)画y=x3+3x-1的图象比较困难,变形为x3=1-3x,画两个函数的图象如何?有惟一解x0∈(0,1)生活中也常常会用到二分法思想: 在一个风雨交加的夜里,从某水库闸房到防洪指挥部的电话线路发生了故障。这是一条10km长的线路,如何迅速查出故障所在?
???????如果沿着线路一小段一小段查找,困难很多。每查一个点要爬一次电线杆子,10km长,大约有200多根电线杆子呢。
???????想一想,维修线路的工人师傅怎样工作最合理?答 案:四、课堂小结1.明确二分法是一种求一元方程近似解的常用方法。
2.二分法求方程的近似解的步骤。
3.数学来源于生活,又应用于生活。
4.本节课充分体现了数学中的四大数学思想,即:……以及无限逼近的思想。
(2.5,3)(2.5,2.75)(2.5,2.625)(2.5,2.5625)(2.53125,2.5625) (2.53125,2.546875) (2.53125,2.5390625) 给定精确度,用二分法求函数零点x0的步骤: 1:确定初始区间[a,b],验证f(a)f(b)<0
2:求区间[a,b]的中点x1=
3:计算:f(x1)判断:
(1)如果f(x1)=0,则x1就是f(x)的零点,计算终止;
(2)如果f(a)f(x1)<0,则令b=x1 (此时零点x0∈(a,x1)中)
(3)如果f(a)f(x1)>0,则令a=x1(此时零点x0∈(x1,b)中)
4:判断是否达到精确度ε:若达到,则得到零点近似值是(a,b)区间内的一点;否则重复2~4步骤。 流程图即:找一个初始区间初始区间长度尽量小,一般通过作图来控制其区间长度↓计算区间中点的函数值是否为0↓是结束运算↓否找出新的端点异号区间是否满足精确度↓↓是→否例题:利用计算器,求方程2x=4-x的近似解 (精确到0.1)怎样找到它的解所在的区间呢?在同一坐标系内画函数y=2x
与y=4-x的图象,如图:提问:能否不画图确定根所在的区间?得:方程有一个解x0 ∈(0,4)如果画得很准确,可得x0 ∈(1,2)数学运用三、练习巩固:练习1:选择题
(1).下列函数的图象与x轴均有交点,其中不能用二分法求其零点的是 ( )C问题:根据练习1,请思考利用二分法求函数
零点的条件是什么? 1、函数y=f (x)在[a,b]上连续不断。2、 y=f (x)满足 f (a)f (b)<0,则在(a,b)内必有零点(2). 方程lnx+2x=6在区间上的根必定属于区间( )
?(A)(-2,1) (B)( ,4)
(C) (1, ) (D) ( , )
??(3).下列函数图像与x轴均有交点,但不宜用二分法求交点横坐标的是( )ABCDBB练习2:
求方程x3+3x-1=0的一个近似解(精确到 0.01)画y=x3+3x-1的图象比较困难,变形为x3=1-3x,画两个函数的图象如何?有惟一解x0∈(0,1)生活中也常常会用到二分法思想: 在一个风雨交加的夜里,从某水库闸房到防洪指挥部的电话线路发生了故障。这是一条10km长的线路,如何迅速查出故障所在?
???????如果沿着线路一小段一小段查找,困难很多。每查一个点要爬一次电线杆子,10km长,大约有200多根电线杆子呢。
???????想一想,维修线路的工人师傅怎样工作最合理?答 案:四、课堂小结1.明确二分法是一种求一元方程近似解的常用方法。
2.二分法求方程的近似解的步骤。
3.数学来源于生活,又应用于生活。
4.本节课充分体现了数学中的四大数学思想,即:……以及无限逼近的思想。
