广东省惠州市第一中学2021-2022学年九年级下学期寒假学生自测自评(开学考试)数学试题(无答案)
文档属性
| 名称 | 广东省惠州市第一中学2021-2022学年九年级下学期寒假学生自测自评(开学考试)数学试题(无答案) | 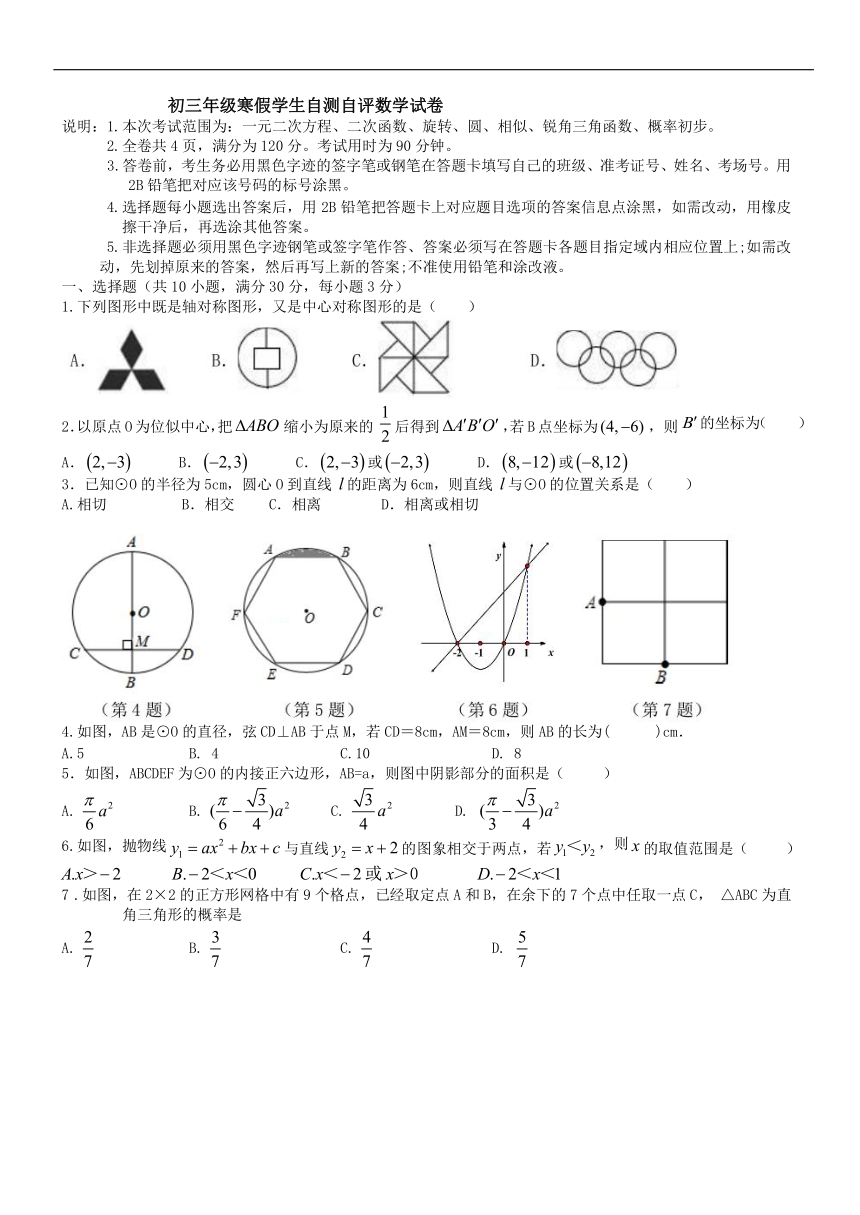 | |
| 格式 | docx | ||
| 文件大小 | 263.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-18 11:01:40 | ||
图片预览


文档简介
初三年级寒假学生自测自评数学试卷
说明:1.本次考试范围为:一元二次方程、二次函数、旋转、圆、相似、锐角三角函数、概率初步。
2.全卷共 4 页,满分为 120 分。考试用时为 90 分钟。
3.答卷前,考生务必用黑色字迹的签字笔或钢笔在答题卡填写自己的班级、准考证号、姓名、考场号。用
2B 铅笔把对应该号码的标号涂黑。
4.选择题每小题选出答案后,用 2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮 擦干净后,再选涂其他答案。
5.非选择题必须用黑色字迹钢笔或签字笔作答、答案必须写在答题卡各题目指定域内相应位置上;如需改
动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
一、选择题(共 10 小题,满分 30 分,每小题 3 分)
1.下列图形中既是轴对称图形,又是中心对称图形的是( )
2.以原点 O 为位似中心,把 ABO 缩小为原来的 后得到 ABO ,若 B 点坐标为 (4, 6) ,则B 的坐标为( )
A. 2, 3 B. 2, 3 C. 2, 3 或 2, 3 D. 8, 12 或 8,12
3.已知⊙O 的半径为 5cm,圆心 O 到直线l 的距离为 6cm,则直线l 与⊙O 的位置关系是( )
A.相切 B.相交 C.相离 D.相离或相切
4.如图,AB 是⊙O 的直径,弦 CD⊥AB 于点 M,若 CD=8cm,AM=8cm,则 AB 的长为( )cm.
A.5 B. 4 C.10 D. 8
5.如图,ABCDEF 为⊙O 的内接正六边形,AB=a,则图中阴影部分的面积是( )
A. B. C. D.
6.如图,抛物线与直线的图象相交于两点,若y1<y2 ,则 x的取值范围是( )
A.x> 2 B. 2<x<0 C.x< 2或x>0 D. 2<x<1
7 .如图,在 2×2 的正方形网格中有 9 个格点,已经取定点 A 和 B,在余下的 7 个点中任取一点 C, △ABC 为直角三角形的概率是
A. B. C. D.
(第 8 题) (第 9 题) (第 10 题) (第 15 题)
8.如图,已知⊙O 是△ABC 的内切圆,且∠ABC=50°,∠ACB=80°.则∠BOC 等于( ) A.125° B.120° C.115° D.100°
9. 如图, ABCD 对角线 AC 与 BD 交于点 O,且 AD=3,AB=5,在 AB 延长线上取一点 E,使 BE AB ,连接
OE 交 BC 于 F,则 BF 的长为( )
A. B. C. D. 1
10. 如图,AB 为⊙O 的直径,C 为⊙O 上一点,其中 AB=4,∠AOC=120°,P 为⊙O 上的动点,连 AP,取 AP 中
点 Q,连 CQ,则线段 CQ 的最大值为( )
A. 3 B. 1 C. 1 3 D. 1
二.填空题(共 7 小题,满分 28 分,每小题 4 分)
11.关于 x 的一元二次方程 x2+bx-10=0 的一个根为 2,则 b 的值为 .
12.有一个只放满形状大小都一样的白色小球的不透明盒子,小刚想知道盒内有多少白球,于是小刚向这个盒中 放了 8 个黑球(黑球的形状大小与白球一样),摇匀后从中随机摸出一个球记下颜色,再把它放回盒中,不断 重复,共摸球 400 次,其中 80 次摸到黑球,估计盒中大约有白球 个
13.烟花厂为咸宁温泉旅游节特别设计制作一种新型礼炮,这种礼炮的升空高 h(m)与飞行时间 t(s)的关系
式是 h t 2 20t 1 ,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要时间为 .
14.一个形如圆锥的冰淇淋纸筒,其底面半径为 3cm ,母线长为12cm ,围成这样的冰淇淋纸筒所需扇形纸片 的圆心角的度数为 .
15.如图,△ABC 的顶点都是正方形网格中的格点,则 cos∠ABC 等于 .
16.如图,将△ABC 绕点 A 旋转到△AEF 的位置,点 E 在 BC 边上,EF 与 AC 交于点
G.若∠B=70°,∠C=25°,则∠FGC= °.
17.如图,在正方形 ABCD 中,以 BC 为边作等边△BPC,延长 BP,CP 分别交 AD 于
点 E,F,连接 BD、DP、BD 与 CF 相交于点 H,给出下列结论:①AE= CF;
②∠BPD=135°;③△PDE∽△DBE; ④ED2=EP EB;其中正确的是 .
三.解答题(一)(共 3 小题,每题 6 分,满分 18 分)
18.
19.如图,在正方形 ABCD 中,点 E、F、G 分别在 AB、BC、CD 上,且 EF⊥FG 于 F.
(
)(1)求证:△BEF∽△CFG;
(2)若 AB=12,AE=3,CF=4,求 CG 的长.
20.如图,小山岗的斜坡 AC 的坡度是 tanα =,在与山脚 C 距离 200 米的 D 处,测得山顶 A 的仰角为 26.6°, 求小山岗的高 AB(结果取整数:参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50).
四.解答题(二)(共 3 小题,每小题 8 分,满分 24 分)
21.甲、乙两所医院分别有一男一女共 4 名医护人员支援湖北武汉抗击疫情.
(1)若从甲、乙两医院支援的医护人员中分别随机选 1 名,则所选的 2 名医护人员性别相同的概率是 ;
(2)若从支援的 4 名医护人员中随机选 2 名,用列表或画树状图的方法求出这 2 名医护人员来自同一所医院 的概率.
22.如图,在 ABC 中,∠C=90°,BD 平分∠ABC 交 AC 于点 D,DE⊥AB 于点 E,AE=6,cosA=.
(1)求 CD 的长;(2)求 tan∠DBC 的值.
(
)
23. 如图,CD 是⊙O 的切线,点 C 在直径 AB 的延长线上. (1)求证:∠CAD=∠BDC;
(2)若 BD AD,AC 3 ,求⊙O 的半径.
五.解答题(三)(共 2 小题,每小题 10 分,满分 20 分)
24.如图,在△ABC 中,AB=AC,以 AB 为直径作⊙O,分别交 BC 于点 D,交 CA 的延长线于点 E,过点 D 作 DH⊥AC
于点 H,连接 DE 交线段 OA 于点 F.
(1)求证:DH 是圆 O 的切线;
(2)若 A 为 EH 的中点,求的值;
(3)若 EA=EF=1,求圆 O 的半径.
25.如图,开口向上的抛物线与 x 轴交于 A( x1 ,0)、B( x2 ,0)两点,与 y 轴交于点 C,且 AC⊥BC,其中 x1 ,
x 2是方程 x2+3x﹣4=0 的两个根.
(1)求点 C 的坐标,并求出抛物线的表达式;
(2)垂直于线段 BC 的直线l 交 x 轴于点 D,交线段 BC 于点 E,连接 CD,求△CDE 的面积的最大值及此时点 D 的 坐标;
(3)在(2)的结论下,抛物线的对称轴上是否存在点 P,使得△PDE 是等腰三角形?若存在,请直接写出点 P
的坐标;若不存在,请说明理由.
说明:1.本次考试范围为:一元二次方程、二次函数、旋转、圆、相似、锐角三角函数、概率初步。
2.全卷共 4 页,满分为 120 分。考试用时为 90 分钟。
3.答卷前,考生务必用黑色字迹的签字笔或钢笔在答题卡填写自己的班级、准考证号、姓名、考场号。用
2B 铅笔把对应该号码的标号涂黑。
4.选择题每小题选出答案后,用 2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮 擦干净后,再选涂其他答案。
5.非选择题必须用黑色字迹钢笔或签字笔作答、答案必须写在答题卡各题目指定域内相应位置上;如需改
动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
一、选择题(共 10 小题,满分 30 分,每小题 3 分)
1.下列图形中既是轴对称图形,又是中心对称图形的是( )
2.以原点 O 为位似中心,把 ABO 缩小为原来的 后得到 ABO ,若 B 点坐标为 (4, 6) ,则B 的坐标为( )
A. 2, 3 B. 2, 3 C. 2, 3 或 2, 3 D. 8, 12 或 8,12
3.已知⊙O 的半径为 5cm,圆心 O 到直线l 的距离为 6cm,则直线l 与⊙O 的位置关系是( )
A.相切 B.相交 C.相离 D.相离或相切
4.如图,AB 是⊙O 的直径,弦 CD⊥AB 于点 M,若 CD=8cm,AM=8cm,则 AB 的长为( )cm.
A.5 B. 4 C.10 D. 8
5.如图,ABCDEF 为⊙O 的内接正六边形,AB=a,则图中阴影部分的面积是( )
A. B. C. D.
6.如图,抛物线与直线的图象相交于两点,若y1<y2 ,则 x的取值范围是( )
A.x> 2 B. 2<x<0 C.x< 2或x>0 D. 2<x<1
7 .如图,在 2×2 的正方形网格中有 9 个格点,已经取定点 A 和 B,在余下的 7 个点中任取一点 C, △ABC 为直角三角形的概率是
A. B. C. D.
(第 8 题) (第 9 题) (第 10 题) (第 15 题)
8.如图,已知⊙O 是△ABC 的内切圆,且∠ABC=50°,∠ACB=80°.则∠BOC 等于( ) A.125° B.120° C.115° D.100°
9. 如图, ABCD 对角线 AC 与 BD 交于点 O,且 AD=3,AB=5,在 AB 延长线上取一点 E,使 BE AB ,连接
OE 交 BC 于 F,则 BF 的长为( )
A. B. C. D. 1
10. 如图,AB 为⊙O 的直径,C 为⊙O 上一点,其中 AB=4,∠AOC=120°,P 为⊙O 上的动点,连 AP,取 AP 中
点 Q,连 CQ,则线段 CQ 的最大值为( )
A. 3 B. 1 C. 1 3 D. 1
二.填空题(共 7 小题,满分 28 分,每小题 4 分)
11.关于 x 的一元二次方程 x2+bx-10=0 的一个根为 2,则 b 的值为 .
12.有一个只放满形状大小都一样的白色小球的不透明盒子,小刚想知道盒内有多少白球,于是小刚向这个盒中 放了 8 个黑球(黑球的形状大小与白球一样),摇匀后从中随机摸出一个球记下颜色,再把它放回盒中,不断 重复,共摸球 400 次,其中 80 次摸到黑球,估计盒中大约有白球 个
13.烟花厂为咸宁温泉旅游节特别设计制作一种新型礼炮,这种礼炮的升空高 h(m)与飞行时间 t(s)的关系
式是 h t 2 20t 1 ,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要时间为 .
14.一个形如圆锥的冰淇淋纸筒,其底面半径为 3cm ,母线长为12cm ,围成这样的冰淇淋纸筒所需扇形纸片 的圆心角的度数为 .
15.如图,△ABC 的顶点都是正方形网格中的格点,则 cos∠ABC 等于 .
16.如图,将△ABC 绕点 A 旋转到△AEF 的位置,点 E 在 BC 边上,EF 与 AC 交于点
G.若∠B=70°,∠C=25°,则∠FGC= °.
17.如图,在正方形 ABCD 中,以 BC 为边作等边△BPC,延长 BP,CP 分别交 AD 于
点 E,F,连接 BD、DP、BD 与 CF 相交于点 H,给出下列结论:①AE= CF;
②∠BPD=135°;③△PDE∽△DBE; ④ED2=EP EB;其中正确的是 .
三.解答题(一)(共 3 小题,每题 6 分,满分 18 分)
18.
19.如图,在正方形 ABCD 中,点 E、F、G 分别在 AB、BC、CD 上,且 EF⊥FG 于 F.
(
)(1)求证:△BEF∽△CFG;
(2)若 AB=12,AE=3,CF=4,求 CG 的长.
20.如图,小山岗的斜坡 AC 的坡度是 tanα =,在与山脚 C 距离 200 米的 D 处,测得山顶 A 的仰角为 26.6°, 求小山岗的高 AB(结果取整数:参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50).
四.解答题(二)(共 3 小题,每小题 8 分,满分 24 分)
21.甲、乙两所医院分别有一男一女共 4 名医护人员支援湖北武汉抗击疫情.
(1)若从甲、乙两医院支援的医护人员中分别随机选 1 名,则所选的 2 名医护人员性别相同的概率是 ;
(2)若从支援的 4 名医护人员中随机选 2 名,用列表或画树状图的方法求出这 2 名医护人员来自同一所医院 的概率.
22.如图,在 ABC 中,∠C=90°,BD 平分∠ABC 交 AC 于点 D,DE⊥AB 于点 E,AE=6,cosA=.
(1)求 CD 的长;(2)求 tan∠DBC 的值.
(
)
23. 如图,CD 是⊙O 的切线,点 C 在直径 AB 的延长线上. (1)求证:∠CAD=∠BDC;
(2)若 BD AD,AC 3 ,求⊙O 的半径.
五.解答题(三)(共 2 小题,每小题 10 分,满分 20 分)
24.如图,在△ABC 中,AB=AC,以 AB 为直径作⊙O,分别交 BC 于点 D,交 CA 的延长线于点 E,过点 D 作 DH⊥AC
于点 H,连接 DE 交线段 OA 于点 F.
(1)求证:DH 是圆 O 的切线;
(2)若 A 为 EH 的中点,求的值;
(3)若 EA=EF=1,求圆 O 的半径.
25.如图,开口向上的抛物线与 x 轴交于 A( x1 ,0)、B( x2 ,0)两点,与 y 轴交于点 C,且 AC⊥BC,其中 x1 ,
x 2是方程 x2+3x﹣4=0 的两个根.
(1)求点 C 的坐标,并求出抛物线的表达式;
(2)垂直于线段 BC 的直线l 交 x 轴于点 D,交线段 BC 于点 E,连接 CD,求△CDE 的面积的最大值及此时点 D 的 坐标;
(3)在(2)的结论下,抛物线的对称轴上是否存在点 P,使得△PDE 是等腰三角形?若存在,请直接写出点 P
的坐标;若不存在,请说明理由.
同课章节目录
