人教版数学八下第16章 二次根式 作业设计(表格式,含答案)
文档属性
| 名称 | 人教版数学八下第16章 二次根式 作业设计(表格式,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 548.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-18 14:15:59 | ||
图片预览




文档简介
第16章 二次根式作业设计
使用时段 作业内容 作业设计
课前 基础性作业 1.若则叫做的 。记作: 其中 叫做的算数平方根。 注:表示7的 平方根。 2.正数的算数平方根是 数(填“正”或“负”) 0的算数平方根是 , 没有平方根.
发展性作业 根据图1—1所示的等边三角形、正方形的条件,完成以下填空: 三角形的高为4cm则边长是_________。 正方形的边长是____________; 问:你认为所得的各代数式的共同特点 是_________
课中 基础性作业 1.下列式子中,不是二次根式的是( ) A. B. C.-1 D. 2.下列各式:,,,,中,一定是二次根式的有( ) A.2个 B.3个 C.4个 D.5个 3.二次根式中字母的取值可以是( ) A.-1 B.- C.-2 D.1 4.要使式子有意义,字母的取值范围必须满足_______. 5.已知实数m,n满足+=0,则=_______,=_______ .
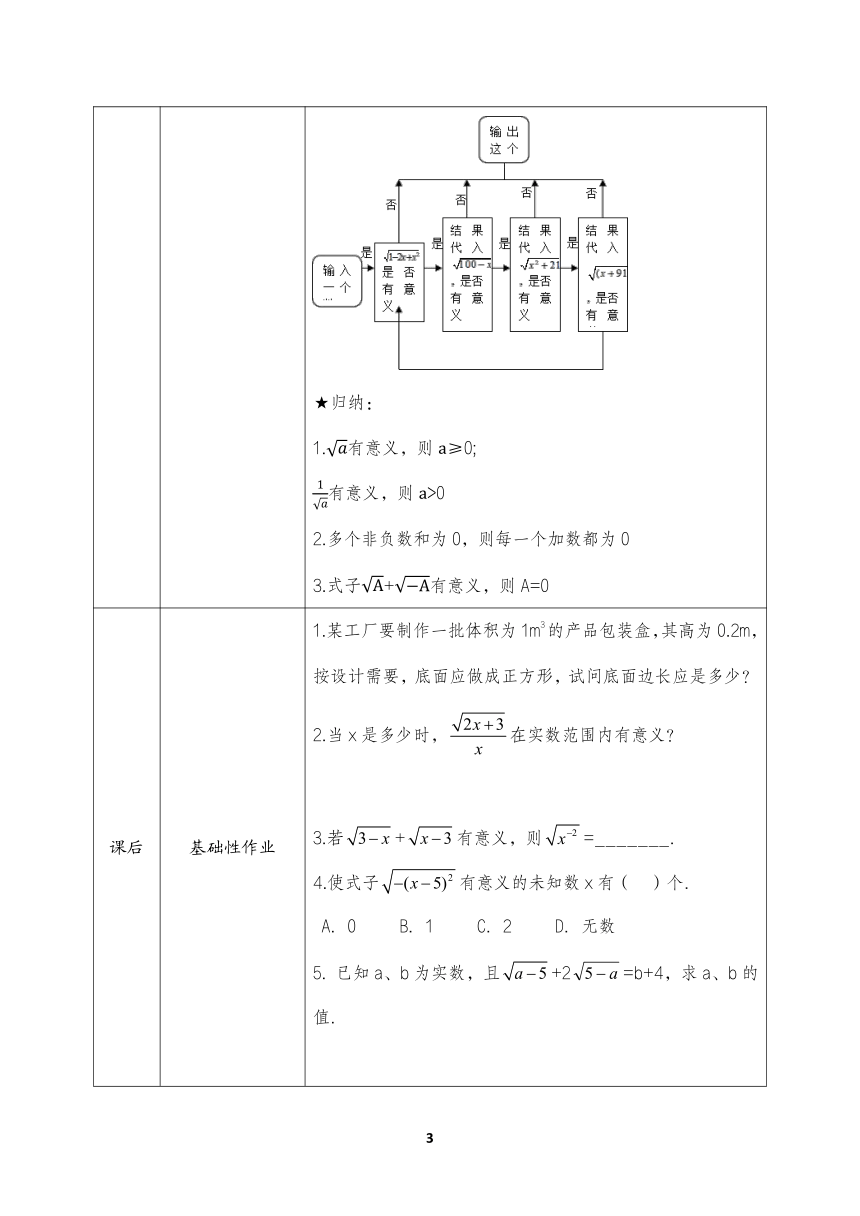
发展性作业 1.式子有意义,则x的取值范围:________ 2.已知x,y都是实数,且y=++3,求xy的值. 3.若,则的值. 4.按下列程序运算,全班分成4个组,当x=1时,每人做一步,看哪一组完成得快.x 取其他数试一试. ★归纳: 1.有意义,则≥0; 有意义,则>0 2.多个非负数和为0,则每一个加数都为0 3.+有意义,则A=0
课后 基础性作业 1.某工厂要制作一批体积为1m3的产品包装盒,其高为0.2m,按设计需要,底面应做成正方形,试问底面边长应是多少? 2.当x是多少时,在实数范围内有意义? 3.若+有意义,则=_______. 4.使式子有意义的未知数x有( )个. A.0 B.1 C.2 D.无数 已知a、b为实数,且+2=b+4,求a、b的值.
发展性作业 1.(跨学科融合)(运算能力、应用意识)射击时,子弹射出枪口时的速度可用公式v=进行计算,其中a为子弹的加速度,s为枪筒的长.如果a=5×105 m/s2,s=0.64 m,那么子弹射出枪口时的速度(用科学记数法表示)为( ) A.0.4×103 m/s B.0.8×103 m/s C.4×102 m/s D.8×102 m/s 2.一个圆的半径为1 cm,和它等面积的正方形的边长是多少厘米(结果精确到0.01 cm) 3.已知一个大圆的面积是两个小圆的面积之和,如果大圆的半径为r cm,两个小圆的半径分别为2 cm和3 cm,求r的值.
使用时段 作业内容 作业设计
课前 基础性作业 当a>0时,表示a的算术平方根,因此>0;当a=0时,表示0的算术平方根,因此=0.这就是说,当 a≥0 时,≥0. 当_____时,是二次根式; (2)当x______时,在实数范围内有意义; (3)已知,则2x+y=_____.
发展性作业 根据算术平方根的意义填空: __________; _________; __________; __________. 一般地,(a≥0) 填空: ________;__________;__________;__________. 一般地,根据算术平方根的意义,(a≥0).
课中 基础性作业 1.下列式子中,计算正确的是( ) A.=- B.-=-0.6 C.=13 D.=36 2.已知是整数,则正整数n的最小值是( ) A.4 B.2 C.3 D.0 3.若实数a,b,c在数轴上的位置如图,则化简:-|b-c|= . 4.若=3-x,则x的取值范围是 . 5.已知一个圆柱体的体积为V,高为h,求它的底面半径r(用含有V和h的代数式表示);当V=80π,h=5时,求底面半径r的值.
发展性作业 下列各式正确的是( ) =-3 B.- =-3 C. =D. =3 2.计算(-)2+的结果是( ) A.-2 B.-24 C.2 D.24 3.当a≤0时,=__________ 4.计算: (1) =______ (2)()2=__________ =_______ (4)=__________ 5.若=5-x,则x的取值范围是__________ 6.实数a,b在数轴上的位置如图所示,则+a的化简的结果为________. ★归纳: 1.=a(a≥0) 2.=|a|
课后 基础性作业 1.下列计算正确的是( ) A.=a C.=±a 2.实数x,y满足+4+4xy+=0,则的值为( ) A.16 B. 3.计算: (1); .
发展性作业 1.若化简|1-x|-的结果为2x-5,则x的取值范围是 . 2.(探究)我们发现: =3, =3, =3, ……, =3, 一般地,对于正整数a,b,如果满足=a, 那么称(a,b)为一组完美方根数对.如上面(3,6)是一组完美方根数对.下面4个结论:①(4,12)是完美方根数对;②(9,91)是完美方根数对;③若(a,380)是完美方根数对,则a2-a=380;④若(x,y)是完美方根数对,则x、y满足y=x2-x.其中正确的结论有 ( ) 1个 B. 2个 C. 3个 D. 4个
使用时段 作业内容 作业设计
课前 基础性作业 计算下列各式,观察计算结果,你能发现什么规律? ×=______,=_______. ×=______,=_____. ×=_____,=______. 共同发现并总结式子有什么规律,用字母等式表达你发现的规律。
发展性作业 利用你的发现检验下列各等式成立的是( ) A.4×2=8 B.5×4=20 C.4×3=7 D.5×4=20
课中 基础性作业 1.计算: ×; ×; ·; (4)-5×6. 2.化简: (1);(2);(3);(4). 3.比较大小:3 4.
发展性作业 1.化简的结果是( ) A.2 B.-2 C.-4 D.4 2.填空:(1)= ; (2)·= . 3.若点P(x,y)在第二象限,则化简的结果是 . 4.已知x为奇数,且,求的值. ★归纳: = = 2.= 注意:上述公式可以推广到多个根式都成立,其中a,b,c都是非负数,反也成立.
课后 基础性作业 1.计算: ×; ×; (3)2·. 2.化简: ×; ; 3.一个长方形的长和宽分别是 cm和2 cm,则这个长方形的面积为___________cm2.
发展性作业 如果,请写出一个满足条件的x的值: . 2.【运算能力、学科融合】根据爱因斯坦的相对论可知,当地面上经过1秒钟时,宇宙飞船内只经过秒.公式内的v是指宇宙飞船的速度,c是指光速(约30万千米/秒).假设有一对亲兄弟,哥哥23岁,弟弟20岁,哥哥在以光速的0.98的速度飞行的宇宙飞船内进行了5年旅行,这5年是地面上的5年,所以弟弟25岁,可是哥哥在这段时间只长了1岁,只有24岁,这样弟弟反而比哥哥大了1岁.请你用上面的公式验证这个结论.
使用时段 作业内容 作业设计
课前 基础性作业 1.填空: (1)=____,=____; (2)=____,=____; (3)=____,=____; (4)=____,=_____. 2.提出问题:你能用字母表示你发现的规律吗?
发展性作业 利用你上述发现的规律,完成下列计算: 1.计算:(1);(2)÷. 2.化简:(1);(2).
课中 基础性作业 1.下列根式中,不是最简二次根式的是( ) A. B. C. D. 2.若a=,b=,则( ) A.a,b互为相反数 B.a,b互为倒数 C.ab=5 D.a=b 3.把化简后得 . 4.若二次根式是最简二次根式,则正整数a的最小值为 . 5.计算: (1)÷×; (2)÷(-)×3. 6.设长方形的面积为S,相邻两边长分别为a,b.已知S=2,b=,求a.
发展性作业 1.已知ab>0,a+b<0,给出下列各式:①=;②·=1;③÷=-b.其中正确的个数是( )A.0 B.1 C.2 D.3 2. 现有一个体积为120 cm3的长方体,它的高为2 cm,长为3 cm,则这个长方体的宽为_ cm. 3. 已知等式=成立,化简|x-6|+的值为 . ★归纳: 1.通过适当的变形化去代数式分母中根号的运算这个过程叫做分母有理化.在根式运算中把一个根式化成最简分式时,都要将分母有理化. 2.最简二次根式满足的两个条件: (1)被开方数不含分母; (2)被开方数中不含能开的尽方的因数或因式.
课后 基础性作业 1.计算: (1); (2)÷. 2.下列二次根式中,是最简二次根式的是( ) A. B. C. D. 3.把下列二次根式化简为最简二次根式: (1); (2) ; (3); (4). 4.计算: (1) ÷ × ; (2)÷×; (3)×4 ÷ .
发展性作业 1.[邵阳中考]在如图方格中,若要使横、竖、斜对角的3个实数相乘都得到同样的结果,则两个空格的实数之积为 . 32163
2.(纠错题)在学完“二次根式的乘除”后,老师给同学们留下这样一道思考题:已知x+y=-6,xy=4,求+的值. 小刚是这样解的: +=+=+=, 把x+y=-6,xy=4代入,得==-3. ∴+的值为-3. 显然,这个解法是错误的,请你写出正确的解题过程.
使用时段 作业内容 作业设计
课前 基础性作业 1.(1)2x和5x________(填“是”或“不是”)同类项,所以2x+5x=________; (2)3和-_______(填“是”或“不是”)同类项, 所以3a+2-=________. 2.类比: 猜一猜:(1)+2=______ (2)+=______
发展性作业 1.化简:(1);(2);(3). 2.下列计算是否正确?为什么? (1)-=; (2)+=; (3)×=; (4)3-=2. 3.计算:(1)-; (2)+.
课中 基础性作业 1.计算: (1)+; (2)-2+. 2.计算: (1)2-6+3; (2)(+)+(-).
发展性作业 1.已知-=a-2=b,则a+b= . 2.若最简二次根式与可以合并,则a的值为 . 3.计算+的值是 . 4.若二次根式-3与的和是一个二次根式,且是最简二次根式,则正整数a的最小值为 ,其和为 . ★归纳: 1.同类二次根式:化简以后被开方数相同的二次根式,成为同类二次根式。 2.二次根式加减时,可以先将二次根式化为最简二次根式,再将被开方数相同的二次根式进行合并。
课后 基础性作业 1.计算3+的值是( ) A.5 B.6 C.4 D.2 2.下列根式中可以与合并的是( ) A. B. C. D. 3.下列计算正确的是( ) A.5-4=1 B.+= C.-= D.3+2=5 4.三角形的三边长分别为cm,cm, cm,则这个三角形的周长为 cm. 5.计算: (1)5-2+; (2)2-+.
发展性作业 1.已知实数a,b,c满足|a―|++=0. (1)求a,b,c的值; (2)以a,b,c为边能否构成三角形?并说明你的理由. 2.已知最简二次根式与是同类二次根式. (1)求出a的值; (2)若a≤x≤2a, 化简:+.
使用时段 作业内容 作业设计
课前 基础性作业 教师节快要到了,为了表达对老师的敬意,小波做了两张大小不同的正方形壁画准备送给老师,其中一张面积为100 cm2,另一张面积为4 00 cm2,他准备再用金彩带镶边.他现在有一条1.2 m的金彩带,请你帮忙算一算,他的金彩带够用吗?
发展性作业 利用你上述发现的规律,计算: (1)(+)×; (2)(4-3)÷2.
课中 基础性作业 1.已知a=+2,b=2-,则的值为( ) A.+2 B.--2 C.1 D.-1 2.计算:(3-)(3+)+(2-). 3.计算: (1)(+3)(-5); (2)(+)(-).
发展性作业 1.已知长方形长,宽. 求长方形的周长; 求与长方形等面积的正方形的周长,并比较长方形周长与正方形周长大小关系. 2.计算直接写结果: __________; __________. 3.把写成的形式为__________. 4.已知,求代数式的值. ★归纳: 1.二次根式的混合运算和实数的运算顺序一致. 2.乘法公式对二次根式同样适用.
课后 基础性作业 1.计算(-)的结果为( ) A. B.- C.-6 D.6- 2.计算(+)(-)的值等于( ) A.2 B.-2 C. D. 3.计算:(+)2-= . 4.计算: (1)÷-×2; ÷(-)-×+. 先化简,再求值:(x+y)(x-y)+y(x+2y)-(x-y)2,其中x=2+,y=2-.
发展性作业 1.若使算式3○的运算结果最小,则○表示的运算符号是( ) A.+ B.- C.× D.÷ 2.若x为实数,在“(+1)□x”的“□”中添上一种运算符号(在“+,-,×,÷”中选择)后,其运算的结果为有理数,则x不可能是( ) A.+1 B.-1 C.2 D.1- 3.(新定义)若规定新运算符号“☆”为a☆b=ab+-,例如:(-2)☆1=(-2)×1+-. (1)求☆的值; (2)求(+)☆的值; (3)若[-(2x-1)]☆=-,求x的值.
16.1二次根式(第1课时:定义)
课前基础性作业答案:
平方根 算术平方根
正 0 负数
课前发展性作业答案:
都含有根号
课中基础性作业答案:
C 2.A 3. D 4.x≥1 5.m=-3,n=1.
课中发展性作业答案:
1.x>2 2.x=2,y=3.原式=8 3.x=2,y=2.原式=0
课后基础性作业答案:
1. 2.x≥且x
3. 4.B 5.a=5,b=-4
课后发展性作业答案:
1.D 2.0.01 3.
16.1二次根式(第2课时:性质)
课前基础性作业答案:
(1)x≤ (2)x<-1 (3)-1
课前发展性作业答案:
4 2 0 a
2 0.1 0 a
课中基础性作业答案:
1.C 2.B 3. -a+b-c 4.x≤3
5.解:圆柱体的体积V=πr2h,所以r=.
把V=80π,h=5代入上式,得r=4.
课中发展性作业答案:
1.B 2.D 3.-a 4. 0.5 m2 81 0.6 5.x≤5 6.-b
课后基础性作业答案:
1.D 2.B 3. (1)1 (2)17
课后发展性作业答案:
1.答案 1≤x≤4
解析:
因为|1-x|-
所以符合题意的x的取值范围是1≤x≤4.
2.C ∵=4,∴(4,12)是完美方根数对,故①正确;∵=
10≠9,∴(9,91)不是完美方根数对,故②不正确;若(a,380)是完美方根数对,则=a,即a2=380+a,所以a2-a=380,故③正确;若(x,y)是完美方根数对,则=x,∴y+x=x2,即y=x2-x,故④正确,故选C.
16.2二次根式的乘除(第1课时:乘法)
课前基础性作业答案:
6 6
20 20
30 30
规律:
课前发展性作业答案:
D
课中基础性作业答案:
解:(1)原式=8.(2)原式=2.(3)原式=.(4)原式=-10.
2.解:(1)原式=12.(2)原式=3.(3)原式=3|xy|.(4)原式=3.
3.>
课中发展性作业答案:
D 2. 4xy 3.-x
4.8≤x≤10
因为x为奇数,所以x=9,
所以=(x-3).
课后基础性作业答案:
1.解:(1)原式=.(2)原式=6.(3)原式=2.
2.解:(1)原式=77.(2)原式=15.(3)原式=2.(4)原式=4|bc|.
3.4
课后发展性作业答案:
1.7(答案不唯一,大于等于6的数均可)
解析 ∵,
∴解得x≥6,
故满足条件的x的值可以为7(答案不唯一,大于等于6的数均可).
2.根据题意得当t地面=1时,t飞船=≈0.2,所以t地面∶t飞船=1∶0.2=5∶1,
即地面上经过5年,宇宙飞船内约经过1年,所以结论是正确的.
16.2二次根式乘除(第2课时:除法)
课前基础性作业答案:
1.(1) (2)
(3) (4)
=
课前发展性作业答案:
解:
原式===2.
(2)原式===3.
课中基础性作业答案:
B 2.D 3. 2 4.2
解:(1)原式=.(2)原式=-3.
6.解:因为S=ab,所以a====
课中发展性作业答案:
1. B ÷===3,故A错误;÷==,故B正确;÷==,故C错误;÷====2,故D错误.
2. 由2x=,知x=÷2=÷===.
3. 解:(1)==.
(2)-÷=-=-=-=-3.
(3)6÷3=(6÷3)·=2=6.
课后基础性作业答案:
1. C 因为ab>0,a+b<0,所以a<0,b<0.①与没有意义,故①错误;②·==1,故②正确;③÷===-b,故③正确.
2. 2 设这个长方体的宽为x cm,根据题意,得3×2×x=120,所以x=2,即这个长方体的宽为2 cm.
3. 4 由题意得,∴3课后发展性作业答案:
1. 6 通解 第一行三个数的乘积为3×2×=6.设第二行中间的数为x,则1×x×6=6,解得x=.设第三行第一个数为y,则y×3×=6,解得y=2,所以两个空格的实数之积为xy=2=6.
秒解 设两个空格的实数分别为x,y,根据题意得xy×=3×2×,所以xy=6.
2. 解:∵x+y=-6,xy=4,∴x<0,y<0,
∴+=--=-.
把x+y=-6,xy=4代入,
得-=-=3.
∴+的值为3.
16.3二次根式加减(第1课时:加法、减法)
课前基础性作业答案:
1.是 7x 不是 5-
2.3 3
课前发展性作业答案:
2.(1)错(2)错(3)对(4)错
3.解:(1)原式=4-3=.
(2)原式=3+5=8.
课中基础性作业答案:
1.(1)解:原式=4+8=12.
(2)解:原式=5-2+3=6.
2.解:
(1)原式=4-2+12=14.
(2)原式=2+2+-=3+.
课中发展性作业答案:
1.答案 6
解析 -=4-2=2,
∵-=a-2=b,
∴a=4,b=2,
∴a+b=4+2=6.
故答案为6.
2.答案 4
解析 ∵最简二次根式与可以合并,
∴3a-1=2a+3,∴a=4,故答案为4.
3.答案 4-1
解析 原式=-1+3=4-1.故答案为4-1.
4.答案 6;-
解析 ∵二次根式-3与的和是一个二次根式,∴两个根式为同类二次根式.
分以下两种情况:
①当是最简二次根式时,∵是最简二次根式,∴3x=2ax,解得a=,不符合题意,舍去;
②当不是最简二次根式时,∵是最简二次根式,且a取最小正整数,
∴=n(n为大于1的正整数),∴a=6.
当a=6时,=2,则-3+=-3+2=-.
课后基础性作业答案:
2.B 3. 4.(5+2)
5.解:(1)原式=13-6.
(2)原式=+.
课后发展性作业答案:
1.(1)由题意得解得 (2)能.理由如下:∵a4,即a+b>c,∴以a,b,c为边能够构成三角形.
2.(1)∵最简二次根式与是同类二次根式,
∴4a-5=13-2a,解得a=3.
(2)把a=3代入a≤x≤2a得3≤x≤6,
则原式
=+=|x-2|+|x-6|=x-2+6-x=4.
16.3二次根式的加减(第2课时:加减混合运算)
课前基础性作业答案:
4×()
=4×()
=120cm
=1.2m
答:够用
课前发展性作业答案:
解:(1)原式=4+3.
(2)原式=2-.
课中基础性作业答案:
B
2.解:原式=9-7+2-2
=2.
3.解:(1)原式=-13-2.(2)原式=2.
课中发展性作业答案:
1.解:长方形的周长为;
长方形的面积为,
则正方形的边长为,
此正方形的周长为,
,,且,
,
则长方形的周长大于正方形的周长.
2.解:,,
故答案为:,;
,
故答案为:;
,
,
,
.
课后基础性作业答案:
B 2.B
3.5
4.解:(1)原式=2-6.
(2)原式=-4.
5.解:原式=x2-y2+xy+2y2-(x2-2xy+y2)
=x2-y2+xy+2y2-x2+2xy-y2
=3xy.
当x=2+,y=2-时,
原式=3×(2+)(2-)
=3×(4-3)
=3.
课后发展性作业答案:
B
解析:
=2,3+2=5,3-2=,3×2=12,3÷2=,由于12>5>>,因此○表示的运算符号是“-”.
2.C [解析] A选项,(+1)-(+1)=0,故A选项不合题意;
B选项,(+1)(-1)=2,故B选项不合题意;
C选项,+1与2无论是相加、相减、相乘、相除,结果都是无理数,故C选项符合题意;
D选项,(+1)(1-)=-2,故D选项不合题意.
故选C.
3.解:(1)☆=×+-
=+-
=9.
(2)(+)☆
=(+)×+-
=12+6+-
=18-.
(3)[-(2x-1)]☆=-可化为
[-(2x-1)]×+3÷-=-,
[-(2x-1)]×=-3,
-(2x-1)=-9,
x=5.
(
7
)
使用时段 作业内容 作业设计
课前 基础性作业 1.若则叫做的 。记作: 其中 叫做的算数平方根。 注:表示7的 平方根。 2.正数的算数平方根是 数(填“正”或“负”) 0的算数平方根是 , 没有平方根.
发展性作业 根据图1—1所示的等边三角形、正方形的条件,完成以下填空: 三角形的高为4cm则边长是_________。 正方形的边长是____________; 问:你认为所得的各代数式的共同特点 是_________
课中 基础性作业 1.下列式子中,不是二次根式的是( ) A. B. C.-1 D. 2.下列各式:,,,,中,一定是二次根式的有( ) A.2个 B.3个 C.4个 D.5个 3.二次根式中字母的取值可以是( ) A.-1 B.- C.-2 D.1 4.要使式子有意义,字母的取值范围必须满足_______. 5.已知实数m,n满足+=0,则=_______,=_______ .
发展性作业 1.式子有意义,则x的取值范围:________ 2.已知x,y都是实数,且y=++3,求xy的值. 3.若,则的值. 4.按下列程序运算,全班分成4个组,当x=1时,每人做一步,看哪一组完成得快.x 取其他数试一试. ★归纳: 1.有意义,则≥0; 有意义,则>0 2.多个非负数和为0,则每一个加数都为0 3.+有意义,则A=0
课后 基础性作业 1.某工厂要制作一批体积为1m3的产品包装盒,其高为0.2m,按设计需要,底面应做成正方形,试问底面边长应是多少? 2.当x是多少时,在实数范围内有意义? 3.若+有意义,则=_______. 4.使式子有意义的未知数x有( )个. A.0 B.1 C.2 D.无数 已知a、b为实数,且+2=b+4,求a、b的值.
发展性作业 1.(跨学科融合)(运算能力、应用意识)射击时,子弹射出枪口时的速度可用公式v=进行计算,其中a为子弹的加速度,s为枪筒的长.如果a=5×105 m/s2,s=0.64 m,那么子弹射出枪口时的速度(用科学记数法表示)为( ) A.0.4×103 m/s B.0.8×103 m/s C.4×102 m/s D.8×102 m/s 2.一个圆的半径为1 cm,和它等面积的正方形的边长是多少厘米(结果精确到0.01 cm) 3.已知一个大圆的面积是两个小圆的面积之和,如果大圆的半径为r cm,两个小圆的半径分别为2 cm和3 cm,求r的值.
使用时段 作业内容 作业设计
课前 基础性作业 当a>0时,表示a的算术平方根,因此>0;当a=0时,表示0的算术平方根,因此=0.这就是说,当 a≥0 时,≥0. 当_____时,是二次根式; (2)当x______时,在实数范围内有意义; (3)已知,则2x+y=_____.
发展性作业 根据算术平方根的意义填空: __________; _________; __________; __________. 一般地,(a≥0) 填空: ________;__________;__________;__________. 一般地,根据算术平方根的意义,(a≥0).
课中 基础性作业 1.下列式子中,计算正确的是( ) A.=- B.-=-0.6 C.=13 D.=36 2.已知是整数,则正整数n的最小值是( ) A.4 B.2 C.3 D.0 3.若实数a,b,c在数轴上的位置如图,则化简:-|b-c|= . 4.若=3-x,则x的取值范围是 . 5.已知一个圆柱体的体积为V,高为h,求它的底面半径r(用含有V和h的代数式表示);当V=80π,h=5时,求底面半径r的值.
发展性作业 下列各式正确的是( ) =-3 B.- =-3 C. =D. =3 2.计算(-)2+的结果是( ) A.-2 B.-24 C.2 D.24 3.当a≤0时,=__________ 4.计算: (1) =______ (2)()2=__________ =_______ (4)=__________ 5.若=5-x,则x的取值范围是__________ 6.实数a,b在数轴上的位置如图所示,则+a的化简的结果为________. ★归纳: 1.=a(a≥0) 2.=|a|
课后 基础性作业 1.下列计算正确的是( ) A.=a C.=±a 2.实数x,y满足+4+4xy+=0,则的值为( ) A.16 B. 3.计算: (1); .
发展性作业 1.若化简|1-x|-的结果为2x-5,则x的取值范围是 . 2.(探究)我们发现: =3, =3, =3, ……, =3, 一般地,对于正整数a,b,如果满足=a, 那么称(a,b)为一组完美方根数对.如上面(3,6)是一组完美方根数对.下面4个结论:①(4,12)是完美方根数对;②(9,91)是完美方根数对;③若(a,380)是完美方根数对,则a2-a=380;④若(x,y)是完美方根数对,则x、y满足y=x2-x.其中正确的结论有 ( ) 1个 B. 2个 C. 3个 D. 4个
使用时段 作业内容 作业设计
课前 基础性作业 计算下列各式,观察计算结果,你能发现什么规律? ×=______,=_______. ×=______,=_____. ×=_____,=______. 共同发现并总结式子有什么规律,用字母等式表达你发现的规律。
发展性作业 利用你的发现检验下列各等式成立的是( ) A.4×2=8 B.5×4=20 C.4×3=7 D.5×4=20
课中 基础性作业 1.计算: ×; ×; ·; (4)-5×6. 2.化简: (1);(2);(3);(4). 3.比较大小:3 4.
发展性作业 1.化简的结果是( ) A.2 B.-2 C.-4 D.4 2.填空:(1)= ; (2)·= . 3.若点P(x,y)在第二象限,则化简的结果是 . 4.已知x为奇数,且,求的值. ★归纳: = = 2.= 注意:上述公式可以推广到多个根式都成立,其中a,b,c都是非负数,反也成立.
课后 基础性作业 1.计算: ×; ×; (3)2·. 2.化简: ×; ; 3.一个长方形的长和宽分别是 cm和2 cm,则这个长方形的面积为___________cm2.
发展性作业 如果,请写出一个满足条件的x的值: . 2.【运算能力、学科融合】根据爱因斯坦的相对论可知,当地面上经过1秒钟时,宇宙飞船内只经过秒.公式内的v是指宇宙飞船的速度,c是指光速(约30万千米/秒).假设有一对亲兄弟,哥哥23岁,弟弟20岁,哥哥在以光速的0.98的速度飞行的宇宙飞船内进行了5年旅行,这5年是地面上的5年,所以弟弟25岁,可是哥哥在这段时间只长了1岁,只有24岁,这样弟弟反而比哥哥大了1岁.请你用上面的公式验证这个结论.
使用时段 作业内容 作业设计
课前 基础性作业 1.填空: (1)=____,=____; (2)=____,=____; (3)=____,=____; (4)=____,=_____. 2.提出问题:你能用字母表示你发现的规律吗?
发展性作业 利用你上述发现的规律,完成下列计算: 1.计算:(1);(2)÷. 2.化简:(1);(2).
课中 基础性作业 1.下列根式中,不是最简二次根式的是( ) A. B. C. D. 2.若a=,b=,则( ) A.a,b互为相反数 B.a,b互为倒数 C.ab=5 D.a=b 3.把化简后得 . 4.若二次根式是最简二次根式,则正整数a的最小值为 . 5.计算: (1)÷×; (2)÷(-)×3. 6.设长方形的面积为S,相邻两边长分别为a,b.已知S=2,b=,求a.
发展性作业 1.已知ab>0,a+b<0,给出下列各式:①=;②·=1;③÷=-b.其中正确的个数是( )A.0 B.1 C.2 D.3 2. 现有一个体积为120 cm3的长方体,它的高为2 cm,长为3 cm,则这个长方体的宽为_ cm. 3. 已知等式=成立,化简|x-6|+的值为 . ★归纳: 1.通过适当的变形化去代数式分母中根号的运算这个过程叫做分母有理化.在根式运算中把一个根式化成最简分式时,都要将分母有理化. 2.最简二次根式满足的两个条件: (1)被开方数不含分母; (2)被开方数中不含能开的尽方的因数或因式.
课后 基础性作业 1.计算: (1); (2)÷. 2.下列二次根式中,是最简二次根式的是( ) A. B. C. D. 3.把下列二次根式化简为最简二次根式: (1); (2) ; (3); (4). 4.计算: (1) ÷ × ; (2)÷×; (3)×4 ÷ .
发展性作业 1.[邵阳中考]在如图方格中,若要使横、竖、斜对角的3个实数相乘都得到同样的结果,则两个空格的实数之积为 . 32163
2.(纠错题)在学完“二次根式的乘除”后,老师给同学们留下这样一道思考题:已知x+y=-6,xy=4,求+的值. 小刚是这样解的: +=+=+=, 把x+y=-6,xy=4代入,得==-3. ∴+的值为-3. 显然,这个解法是错误的,请你写出正确的解题过程.
使用时段 作业内容 作业设计
课前 基础性作业 1.(1)2x和5x________(填“是”或“不是”)同类项,所以2x+5x=________; (2)3和-_______(填“是”或“不是”)同类项, 所以3a+2-=________. 2.类比: 猜一猜:(1)+2=______ (2)+=______
发展性作业 1.化简:(1);(2);(3). 2.下列计算是否正确?为什么? (1)-=; (2)+=; (3)×=; (4)3-=2. 3.计算:(1)-; (2)+.
课中 基础性作业 1.计算: (1)+; (2)-2+. 2.计算: (1)2-6+3; (2)(+)+(-).
发展性作业 1.已知-=a-2=b,则a+b= . 2.若最简二次根式与可以合并,则a的值为 . 3.计算+的值是 . 4.若二次根式-3与的和是一个二次根式,且是最简二次根式,则正整数a的最小值为 ,其和为 . ★归纳: 1.同类二次根式:化简以后被开方数相同的二次根式,成为同类二次根式。 2.二次根式加减时,可以先将二次根式化为最简二次根式,再将被开方数相同的二次根式进行合并。
课后 基础性作业 1.计算3+的值是( ) A.5 B.6 C.4 D.2 2.下列根式中可以与合并的是( ) A. B. C. D. 3.下列计算正确的是( ) A.5-4=1 B.+= C.-= D.3+2=5 4.三角形的三边长分别为cm,cm, cm,则这个三角形的周长为 cm. 5.计算: (1)5-2+; (2)2-+.
发展性作业 1.已知实数a,b,c满足|a―|++=0. (1)求a,b,c的值; (2)以a,b,c为边能否构成三角形?并说明你的理由. 2.已知最简二次根式与是同类二次根式. (1)求出a的值; (2)若a≤x≤2a, 化简:+.
使用时段 作业内容 作业设计
课前 基础性作业 教师节快要到了,为了表达对老师的敬意,小波做了两张大小不同的正方形壁画准备送给老师,其中一张面积为100 cm2,另一张面积为4 00 cm2,他准备再用金彩带镶边.他现在有一条1.2 m的金彩带,请你帮忙算一算,他的金彩带够用吗?
发展性作业 利用你上述发现的规律,计算: (1)(+)×; (2)(4-3)÷2.
课中 基础性作业 1.已知a=+2,b=2-,则的值为( ) A.+2 B.--2 C.1 D.-1 2.计算:(3-)(3+)+(2-). 3.计算: (1)(+3)(-5); (2)(+)(-).
发展性作业 1.已知长方形长,宽. 求长方形的周长; 求与长方形等面积的正方形的周长,并比较长方形周长与正方形周长大小关系. 2.计算直接写结果: __________; __________. 3.把写成的形式为__________. 4.已知,求代数式的值. ★归纳: 1.二次根式的混合运算和实数的运算顺序一致. 2.乘法公式对二次根式同样适用.
课后 基础性作业 1.计算(-)的结果为( ) A. B.- C.-6 D.6- 2.计算(+)(-)的值等于( ) A.2 B.-2 C. D. 3.计算:(+)2-= . 4.计算: (1)÷-×2; ÷(-)-×+. 先化简,再求值:(x+y)(x-y)+y(x+2y)-(x-y)2,其中x=2+,y=2-.
发展性作业 1.若使算式3○的运算结果最小,则○表示的运算符号是( ) A.+ B.- C.× D.÷ 2.若x为实数,在“(+1)□x”的“□”中添上一种运算符号(在“+,-,×,÷”中选择)后,其运算的结果为有理数,则x不可能是( ) A.+1 B.-1 C.2 D.1- 3.(新定义)若规定新运算符号“☆”为a☆b=ab+-,例如:(-2)☆1=(-2)×1+-. (1)求☆的值; (2)求(+)☆的值; (3)若[-(2x-1)]☆=-,求x的值.
16.1二次根式(第1课时:定义)
课前基础性作业答案:
平方根 算术平方根
正 0 负数
课前发展性作业答案:
都含有根号
课中基础性作业答案:
C 2.A 3. D 4.x≥1 5.m=-3,n=1.
课中发展性作业答案:
1.x>2 2.x=2,y=3.原式=8 3.x=2,y=2.原式=0
课后基础性作业答案:
1. 2.x≥且x
3. 4.B 5.a=5,b=-4
课后发展性作业答案:
1.D 2.0.01 3.
16.1二次根式(第2课时:性质)
课前基础性作业答案:
(1)x≤ (2)x<-1 (3)-1
课前发展性作业答案:
4 2 0 a
2 0.1 0 a
课中基础性作业答案:
1.C 2.B 3. -a+b-c 4.x≤3
5.解:圆柱体的体积V=πr2h,所以r=.
把V=80π,h=5代入上式,得r=4.
课中发展性作业答案:
1.B 2.D 3.-a 4. 0.5 m2 81 0.6 5.x≤5 6.-b
课后基础性作业答案:
1.D 2.B 3. (1)1 (2)17
课后发展性作业答案:
1.答案 1≤x≤4
解析:
因为|1-x|-
所以符合题意的x的取值范围是1≤x≤4.
2.C ∵=4,∴(4,12)是完美方根数对,故①正确;∵=
10≠9,∴(9,91)不是完美方根数对,故②不正确;若(a,380)是完美方根数对,则=a,即a2=380+a,所以a2-a=380,故③正确;若(x,y)是完美方根数对,则=x,∴y+x=x2,即y=x2-x,故④正确,故选C.
16.2二次根式的乘除(第1课时:乘法)
课前基础性作业答案:
6 6
20 20
30 30
规律:
课前发展性作业答案:
D
课中基础性作业答案:
解:(1)原式=8.(2)原式=2.(3)原式=.(4)原式=-10.
2.解:(1)原式=12.(2)原式=3.(3)原式=3|xy|.(4)原式=3.
3.>
课中发展性作业答案:
D 2. 4xy 3.-x
4.8≤x≤10
因为x为奇数,所以x=9,
所以=(x-3).
课后基础性作业答案:
1.解:(1)原式=.(2)原式=6.(3)原式=2.
2.解:(1)原式=77.(2)原式=15.(3)原式=2.(4)原式=4|bc|.
3.4
课后发展性作业答案:
1.7(答案不唯一,大于等于6的数均可)
解析 ∵,
∴解得x≥6,
故满足条件的x的值可以为7(答案不唯一,大于等于6的数均可).
2.根据题意得当t地面=1时,t飞船=≈0.2,所以t地面∶t飞船=1∶0.2=5∶1,
即地面上经过5年,宇宙飞船内约经过1年,所以结论是正确的.
16.2二次根式乘除(第2课时:除法)
课前基础性作业答案:
1.(1) (2)
(3) (4)
=
课前发展性作业答案:
解:
原式===2.
(2)原式===3.
课中基础性作业答案:
B 2.D 3. 2 4.2
解:(1)原式=.(2)原式=-3.
6.解:因为S=ab,所以a====
课中发展性作业答案:
1. B ÷===3,故A错误;÷==,故B正确;÷==,故C错误;÷====2,故D错误.
2. 由2x=,知x=÷2=÷===.
3. 解:(1)==.
(2)-÷=-=-=-=-3.
(3)6÷3=(6÷3)·=2=6.
课后基础性作业答案:
1. C 因为ab>0,a+b<0,所以a<0,b<0.①与没有意义,故①错误;②·==1,故②正确;③÷===-b,故③正确.
2. 2 设这个长方体的宽为x cm,根据题意,得3×2×x=120,所以x=2,即这个长方体的宽为2 cm.
3. 4 由题意得,∴3
1. 6 通解 第一行三个数的乘积为3×2×=6.设第二行中间的数为x,则1×x×6=6,解得x=.设第三行第一个数为y,则y×3×=6,解得y=2,所以两个空格的实数之积为xy=2=6.
秒解 设两个空格的实数分别为x,y,根据题意得xy×=3×2×,所以xy=6.
2. 解:∵x+y=-6,xy=4,∴x<0,y<0,
∴+=--=-.
把x+y=-6,xy=4代入,
得-=-=3.
∴+的值为3.
16.3二次根式加减(第1课时:加法、减法)
课前基础性作业答案:
1.是 7x 不是 5-
2.3 3
课前发展性作业答案:
2.(1)错(2)错(3)对(4)错
3.解:(1)原式=4-3=.
(2)原式=3+5=8.
课中基础性作业答案:
1.(1)解:原式=4+8=12.
(2)解:原式=5-2+3=6.
2.解:
(1)原式=4-2+12=14.
(2)原式=2+2+-=3+.
课中发展性作业答案:
1.答案 6
解析 -=4-2=2,
∵-=a-2=b,
∴a=4,b=2,
∴a+b=4+2=6.
故答案为6.
2.答案 4
解析 ∵最简二次根式与可以合并,
∴3a-1=2a+3,∴a=4,故答案为4.
3.答案 4-1
解析 原式=-1+3=4-1.故答案为4-1.
4.答案 6;-
解析 ∵二次根式-3与的和是一个二次根式,∴两个根式为同类二次根式.
分以下两种情况:
①当是最简二次根式时,∵是最简二次根式,∴3x=2ax,解得a=,不符合题意,舍去;
②当不是最简二次根式时,∵是最简二次根式,且a取最小正整数,
∴=n(n为大于1的正整数),∴a=6.
当a=6时,=2,则-3+=-3+2=-.
课后基础性作业答案:
2.B 3. 4.(5+2)
5.解:(1)原式=13-6.
(2)原式=+.
课后发展性作业答案:
1.(1)由题意得解得 (2)能.理由如下:∵a
2.(1)∵最简二次根式与是同类二次根式,
∴4a-5=13-2a,解得a=3.
(2)把a=3代入a≤x≤2a得3≤x≤6,
则原式
=+=|x-2|+|x-6|=x-2+6-x=4.
16.3二次根式的加减(第2课时:加减混合运算)
课前基础性作业答案:
4×()
=4×()
=120cm
=1.2m
答:够用
课前发展性作业答案:
解:(1)原式=4+3.
(2)原式=2-.
课中基础性作业答案:
B
2.解:原式=9-7+2-2
=2.
3.解:(1)原式=-13-2.(2)原式=2.
课中发展性作业答案:
1.解:长方形的周长为;
长方形的面积为,
则正方形的边长为,
此正方形的周长为,
,,且,
,
则长方形的周长大于正方形的周长.
2.解:,,
故答案为:,;
,
故答案为:;
,
,
,
.
课后基础性作业答案:
B 2.B
3.5
4.解:(1)原式=2-6.
(2)原式=-4.
5.解:原式=x2-y2+xy+2y2-(x2-2xy+y2)
=x2-y2+xy+2y2-x2+2xy-y2
=3xy.
当x=2+,y=2-时,
原式=3×(2+)(2-)
=3×(4-3)
=3.
课后发展性作业答案:
B
解析:
=2,3+2=5,3-2=,3×2=12,3÷2=,由于12>5>>,因此○表示的运算符号是“-”.
2.C [解析] A选项,(+1)-(+1)=0,故A选项不合题意;
B选项,(+1)(-1)=2,故B选项不合题意;
C选项,+1与2无论是相加、相减、相乘、相除,结果都是无理数,故C选项符合题意;
D选项,(+1)(1-)=-2,故D选项不合题意.
故选C.
3.解:(1)☆=×+-
=+-
=9.
(2)(+)☆
=(+)×+-
=12+6+-
=18-.
(3)[-(2x-1)]☆=-可化为
[-(2x-1)]×+3÷-=-,
[-(2x-1)]×=-3,
-(2x-1)=-9,
x=5.
(
7
)
