4.3简单线性规划的应用
图片预览






文档简介
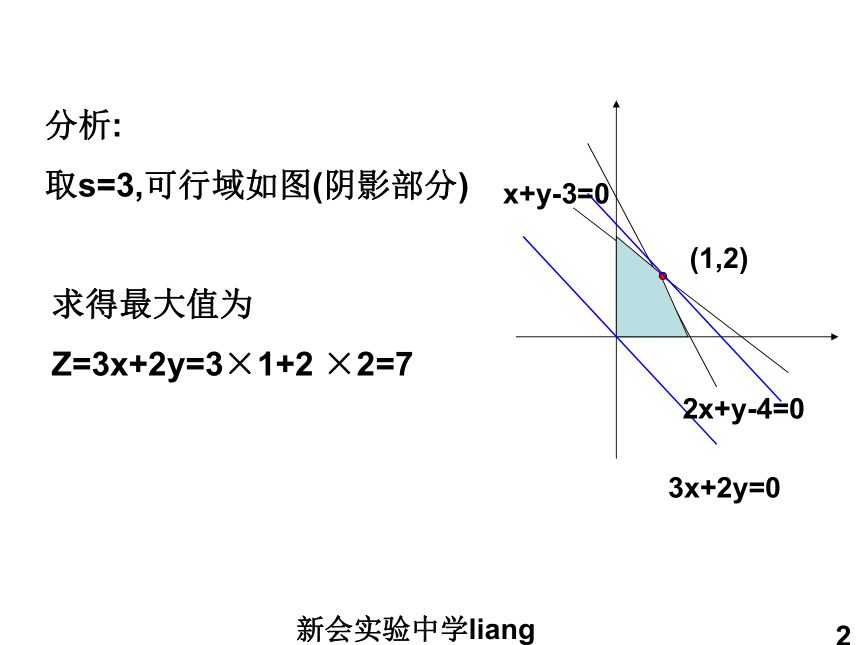
课件25张PPT。新会实验中学liang1D新会实验中学liang23x+2y=02x+y-4=0x+y-3=0(1,2)分析:
取s=3,可行域如图(阴影部分)求得最大值为
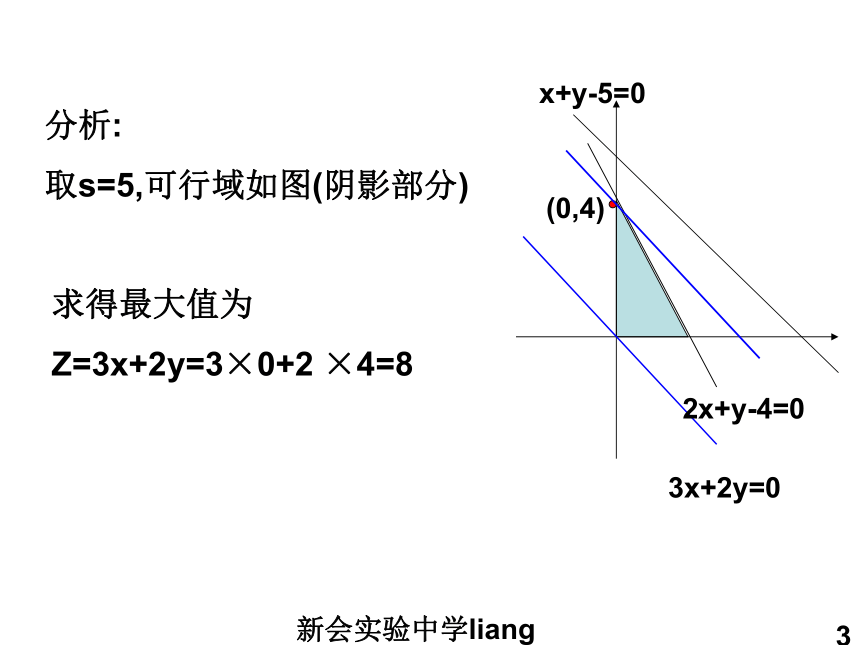
Z=3x+2y=3×1+2 ×2=7新会实验中学liang33x+2y=02x+y-4=0x+y-5=0(0,4)分析:
取s=5,可行域如图(阴影部分)求得最大值为
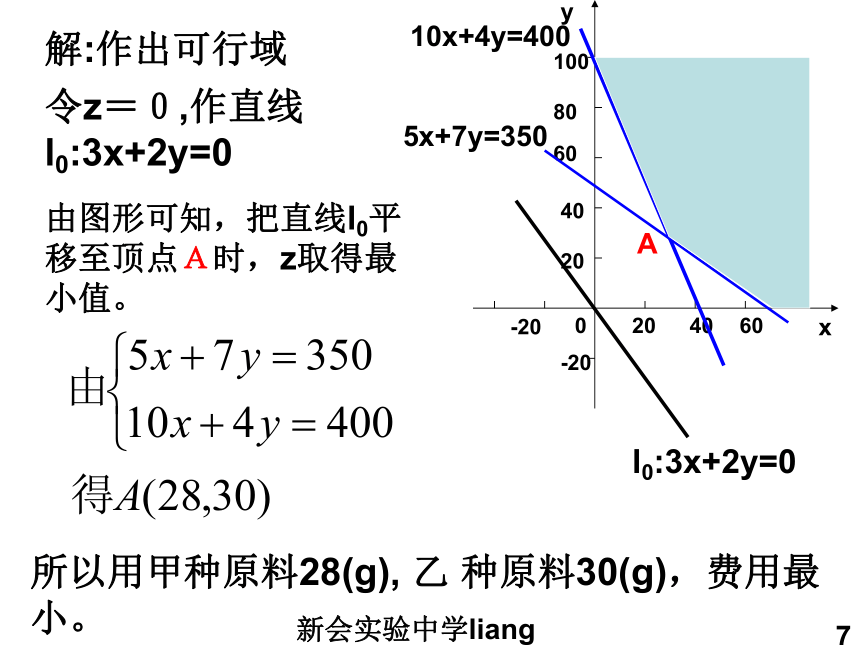
Z=3x+2y=3×0+2 ×4=8新会实验中学liang44.3简单线性规划的应用学习目标:
能从实际情境中抽象出一些简单的二元线
性规划问题,并加以解决.重点:
如何从有关实际问题中抽象出简单的二元线性规划数学模型.新会实验中学liang5例9 医院用甲、乙两种原料为手术后的病人配营养餐,甲种原料每10g含5单位蛋白质和10单位铁质,售价3元;乙种原料每10g含7单位蛋白质和4单位铁质,售价2元.若病人每餐至少需要35单位蛋白质和40单位铁质,试问:应如何使用甲、乙原料,才能既满足营养,又使费用最省?解法1 设甲、乙两种原料分别用xg 和 yg.++≥≥Z=3 +2xy新会实验中学liang6这样,问题成为:在约束条件00Z=3 +2新会实验中学liang7解:作出可行域20-206020040806040100-205x+7y=35010x+4y=400l0:3x+2y=0xy令z=0,作直线l0:3x+2y=0由图形可知,把直线l0平移至顶点A时,z取得最小值。所以用甲种原料28(g), 乙 种原料30(g),费用最小。 A新会实验中学liang8例9 医院用甲、乙两种原料为手术后的病人配营养餐,甲种原料每10g含5单位蛋白质和10单位铁质,售价3元;乙种原料每10g含7单位蛋白质和4单位铁质,售价2元.若病人每餐至少需要35单位蛋白质和40单位铁质,试问:应如何使用甲、乙原料,才能既满足营养,又使费用最省?解法2 设甲、乙两种原料分别用10xg 和 10yg.xyxyxy++≥≥Z=3x+2yxy新会实验中学liang9这样,问题成为:在约束条件新会实验中学liang10解:作出可行域2-2620486410-25x+7y=3510x+4y=40l0:3x+2y=0xy令z=0,作直线l0:3x+2y=0由图形可知,把直线l0平移至顶点A时,z取得最小值。所以用甲种原料 14/5×10=28(g), 乙 种原料3×10=30(g),费用最小。 A新会实验中学liang11简单线性规划应用题的步骤:(1)设出变量(注意实际问题变量的取值范围);
(2)找出约束条件,列出目标函数;
(3)图解可行域(即在可行域内求目标函数的最优解);
(4)回答实际问题。新会实验中学liang12 (2004年江苏)制定投资计划时,不仅要考虑可能获得的盈利,而且考虑可能出现的亏损.某投资人打算投资甲、乙两个项目,根据预测,甲、乙项目可能的最大盈利率分别为100%和50%, 可能的最大亏损率分别为30%和10%,投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元,问投资人对甲、乙两个项目分别投资多少万元,才能使可能的盈利最大?练习分析:设甲、乙两个项目投资分别为x万元,y万元,
盈利z万元.根据题意有:
总投资:x+y
亏损:0.3x+0.1y
盈利:z=x+0.5y新会实验中学liang13新会实验中学liang14 由图形知当直线L向上平移时,所对应的z=x+0.5y的函数值随之增大,所以当直线L经过可行域的顶点M时, z=x+0.5y取得最大值.作出可行域,
令z=o,作直线 l :x+0.5y=0新会实验中学liang15练习:P123 2 3答案:新会实验中学liang16新会实验中学liang17新会实验中学liang18练习 P121 设从A地运往D,E两地的产品为x万吨、y万吨,
则从A地运往F地产品为(1.2-x-y)万吨,
从B地运往D、E、F三地的产品分别为(0.8-x)万吨、(0.6-y)万吨、0.8-(0.8-x)-(0.6-y)=(x+y-0.6)万吨,
总运费约为2万元。新会实验中学liang19xy0Ay=0.6X=0.8 如图所示,作直线l0: -3x+y+10=0.将直线平移
至过点A的位置时,Z取得最小值,
得A(0.8,0 ),
Zmin=-30×0.8+10 ×0+100=76.新会实验中学liang20例10 某厂生产一种产品,其成本为27元/kg,售价为50元/kg,生产中,每千克产品产生0.5m3的污水,污水有两种排放方式:
方式一:直接排入河流。
方式二:经厂内污水处理站处理后排入河流,但受污水处理站技术水平的限制,污水处理率只有85%,污水处理站最大处理能力是0.9m3/h,处理污水的成本是5元/m3.
另外,环保部门对排玉河流的污水收费标准是17.6元/ m3,且允许该厂
排玉河流中污水的最大量是0.225m3/h,那么,该厂应选择怎样的生产与排污方案,可使其每时净收益最大?
新会实验中学liang21分析 为了解决问题,首先,要搞清楚是什么因素决定净收益。净收益=售出产品的收入-生产费用其中生产费用包括生产成本、污水处理费、排污费等。分析过程看课本P120新会实验中学liang22新会实验中学liang23新会实验中学liang24021-1321AyXl09x+170y=450.3x-y=00.3-y=0.9解: 作出可行域,
令z=0作直线 l0:20.708-9.96y=0.
由图形可以看出,平移直线 l0 ,在可行域中
的顶点A处,z取得最大值.新会实验中学liang25作业:P123 B组 2
取s=3,可行域如图(阴影部分)求得最大值为
Z=3x+2y=3×1+2 ×2=7新会实验中学liang33x+2y=02x+y-4=0x+y-5=0(0,4)分析:
取s=5,可行域如图(阴影部分)求得最大值为
Z=3x+2y=3×0+2 ×4=8新会实验中学liang44.3简单线性规划的应用学习目标:
能从实际情境中抽象出一些简单的二元线
性规划问题,并加以解决.重点:
如何从有关实际问题中抽象出简单的二元线性规划数学模型.新会实验中学liang5例9 医院用甲、乙两种原料为手术后的病人配营养餐,甲种原料每10g含5单位蛋白质和10单位铁质,售价3元;乙种原料每10g含7单位蛋白质和4单位铁质,售价2元.若病人每餐至少需要35单位蛋白质和40单位铁质,试问:应如何使用甲、乙原料,才能既满足营养,又使费用最省?解法1 设甲、乙两种原料分别用xg 和 yg.++≥≥Z=3 +2xy新会实验中学liang6这样,问题成为:在约束条件00Z=3 +2新会实验中学liang7解:作出可行域20-206020040806040100-205x+7y=35010x+4y=400l0:3x+2y=0xy令z=0,作直线l0:3x+2y=0由图形可知,把直线l0平移至顶点A时,z取得最小值。所以用甲种原料28(g), 乙 种原料30(g),费用最小。 A新会实验中学liang8例9 医院用甲、乙两种原料为手术后的病人配营养餐,甲种原料每10g含5单位蛋白质和10单位铁质,售价3元;乙种原料每10g含7单位蛋白质和4单位铁质,售价2元.若病人每餐至少需要35单位蛋白质和40单位铁质,试问:应如何使用甲、乙原料,才能既满足营养,又使费用最省?解法2 设甲、乙两种原料分别用10xg 和 10yg.xyxyxy++≥≥Z=3x+2yxy新会实验中学liang9这样,问题成为:在约束条件新会实验中学liang10解:作出可行域2-2620486410-25x+7y=3510x+4y=40l0:3x+2y=0xy令z=0,作直线l0:3x+2y=0由图形可知,把直线l0平移至顶点A时,z取得最小值。所以用甲种原料 14/5×10=28(g), 乙 种原料3×10=30(g),费用最小。 A新会实验中学liang11简单线性规划应用题的步骤:(1)设出变量(注意实际问题变量的取值范围);
(2)找出约束条件,列出目标函数;
(3)图解可行域(即在可行域内求目标函数的最优解);
(4)回答实际问题。新会实验中学liang12 (2004年江苏)制定投资计划时,不仅要考虑可能获得的盈利,而且考虑可能出现的亏损.某投资人打算投资甲、乙两个项目,根据预测,甲、乙项目可能的最大盈利率分别为100%和50%, 可能的最大亏损率分别为30%和10%,投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元,问投资人对甲、乙两个项目分别投资多少万元,才能使可能的盈利最大?练习分析:设甲、乙两个项目投资分别为x万元,y万元,
盈利z万元.根据题意有:
总投资:x+y
亏损:0.3x+0.1y
盈利:z=x+0.5y新会实验中学liang13新会实验中学liang14 由图形知当直线L向上平移时,所对应的z=x+0.5y的函数值随之增大,所以当直线L经过可行域的顶点M时, z=x+0.5y取得最大值.作出可行域,
令z=o,作直线 l :x+0.5y=0新会实验中学liang15练习:P123 2 3答案:新会实验中学liang16新会实验中学liang17新会实验中学liang18练习 P121 设从A地运往D,E两地的产品为x万吨、y万吨,
则从A地运往F地产品为(1.2-x-y)万吨,
从B地运往D、E、F三地的产品分别为(0.8-x)万吨、(0.6-y)万吨、0.8-(0.8-x)-(0.6-y)=(x+y-0.6)万吨,
总运费约为2万元。新会实验中学liang19xy0Ay=0.6X=0.8 如图所示,作直线l0: -3x+y+10=0.将直线平移
至过点A的位置时,Z取得最小值,
得A(0.8,0 ),
Zmin=-30×0.8+10 ×0+100=76.新会实验中学liang20例10 某厂生产一种产品,其成本为27元/kg,售价为50元/kg,生产中,每千克产品产生0.5m3的污水,污水有两种排放方式:
方式一:直接排入河流。
方式二:经厂内污水处理站处理后排入河流,但受污水处理站技术水平的限制,污水处理率只有85%,污水处理站最大处理能力是0.9m3/h,处理污水的成本是5元/m3.
另外,环保部门对排玉河流的污水收费标准是17.6元/ m3,且允许该厂
排玉河流中污水的最大量是0.225m3/h,那么,该厂应选择怎样的生产与排污方案,可使其每时净收益最大?
新会实验中学liang21分析 为了解决问题,首先,要搞清楚是什么因素决定净收益。净收益=售出产品的收入-生产费用其中生产费用包括生产成本、污水处理费、排污费等。分析过程看课本P120新会实验中学liang22新会实验中学liang23新会实验中学liang24021-1321AyXl09x+170y=450.3x-y=00.3-y=0.9解: 作出可行域,
令z=0作直线 l0:20.708-9.96y=0.
由图形可以看出,平移直线 l0 ,在可行域中
的顶点A处,z取得最大值.新会实验中学liang25作业:P123 B组 2
