4.1二元一次不等式(组)与平面区域
图片预览




文档简介
课件16张PPT。新会实验中学liang14 简单线性规划学习目标:
(1)能从实际情境中抽象出二元一次不等式组;
(2)了解二元一次不等式的几何意义;
(3)能用平面区域表示二元一次不等式组;新会实验中学liang2一名刚参加工作的大学生为自己制定的每月用餐费的最低标准是240元,又知其他费用最少需支出180元,而每月可用来支配的资金为500元,这名新员工可以如何使用这些钱?如:用餐费可不可以为300元,可不可以为
350元如:用餐费为280元时,其他费用可不可以
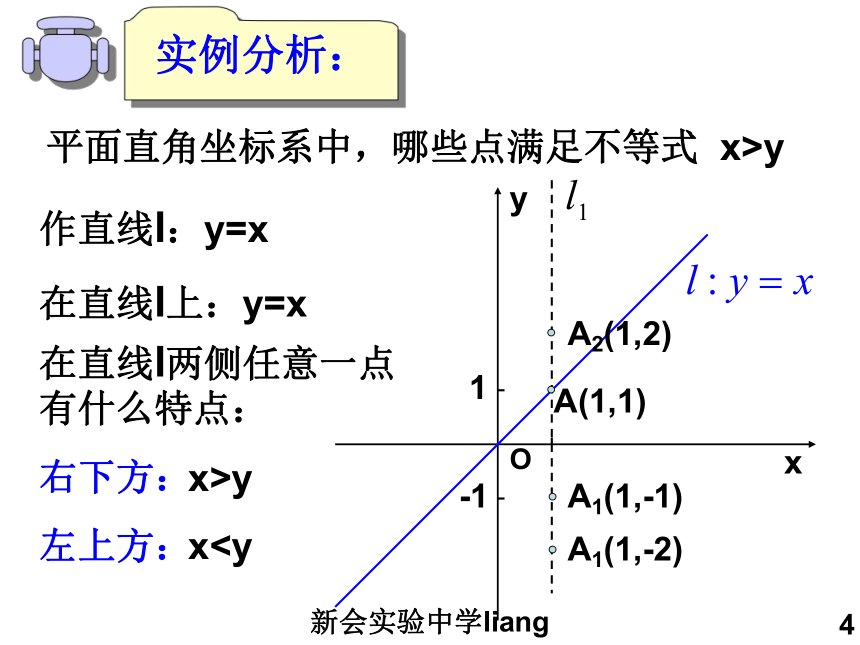
为200元新会实验中学liang3设用餐费为x元,其他费用为y元,由题意:X不小于240,y不小于180,x与y之和不超过500,用不等式组可表示为:不等式组的一个解(x,y)视为直角坐标系上的一个点,如(280,200)表示_______则问题转化为:确定平面直角坐标系中不等式组的解集区域新会实验中学liang4平面直角坐标系中,哪些点满足不等式 x>y作直线l:y=x在直线l两侧任意一点有什么特点:
右下方:
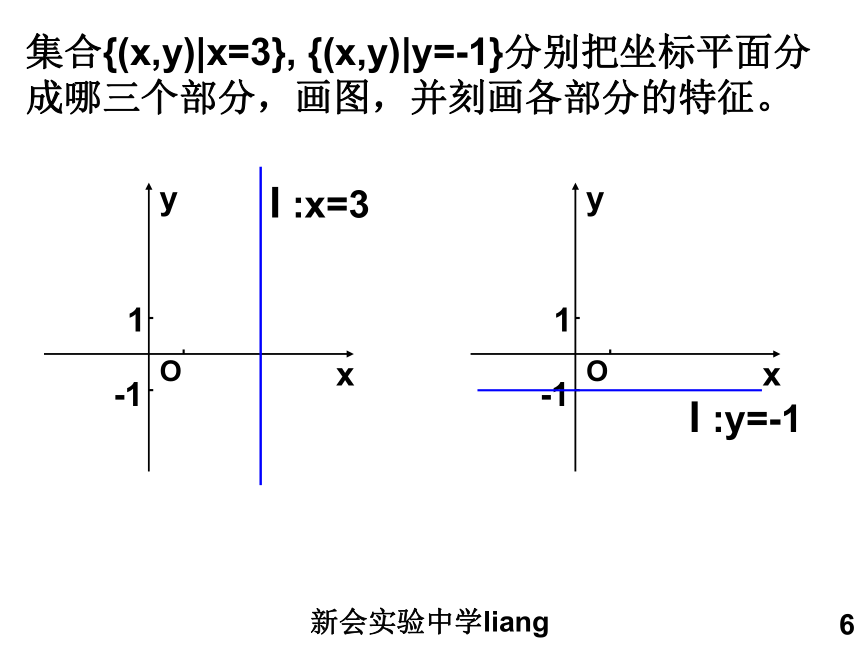
左上方:A(1,1)x>yx0x-y<0新会实验中学liang6集合{(x,y)|x=3}, {(x,y)|y=-1}分别把坐标平面分成哪三个部分,画图,并刻画各部分的特征。新会实验中学liang7例题讲解【例1】
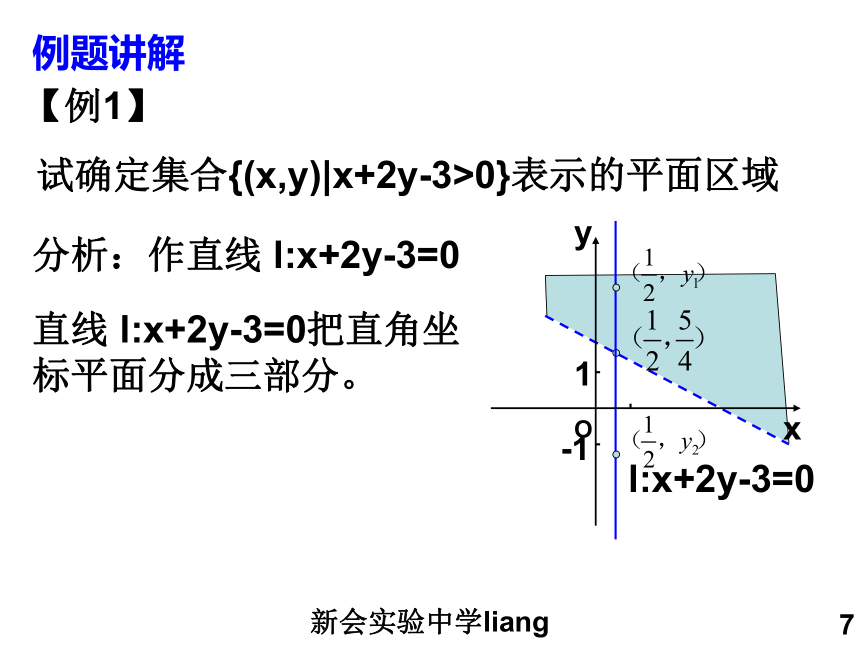
试确定集合{(x,y)|x+2y-3>0}表示的平面区域分析:作直线 l:x+2y-3=0直线 l:x+2y-3=0把直角坐标平面分成三部分。新会实验中学liang8解:直线l将直角平面坐标系分成三部分(l及其两侧)。在l的右上方的平面区域内的任一点的坐标(x,y)满足不等式x+2y-3>0,而另外两部分的点均不满足不等式x+2y-3>0。不等式x+2y-3>0表示的是直线l右上方的平面区域新会实验中学liang9 一般地直线l:ax+by+c=0把直角坐标平面分成了三个部分: (1)直线l上的点(x,y)的坐标满足ax+by+c=0; (2)直线l一侧的平面区域内的点(x,y)的坐标满足ax+by+c>0; (3)直线l另一侧的平面区域内的点(x,y)的坐标满足ax+by+c<0; 只需在直线l的某一侧的平面区域内,任取一特殊点(x0,y0)(一般取原点(0,0)),从ax0+by0+c值的正负得出结论新会实验中学liang10【例2】 画出不等式2x-y-4≤0表示的平面区域。解:先画出直线l:2x-y-4=0,取原点O(0,0),把O点的坐标代入2x-y-4,得 2×0-0-4=-4<0 所以,原点在不等式2x-y-4<0所表示的平面区域内,不等式2x-y-4 ≤0所表示的平面区域是不等式2x-y-4<0所表示的平面区域加上直线l:2x-y-4=0新会实验中学liang11【例2】 画出以下不等式组表示的平面区域。分析:不等式组表示的平面区域是不等式①,
②,③所表示的平面区域的公共部分。新会实验中学liang12如图所示:不等式①表示直线x+y-1=0的右上方(包括直线)的平面区域;不等式②表示直线x-y=0的右下方(包括直线)的平面区域;不等式 ③表示直线x=2的左方(包括直线)的平面区域;所以,原不等式组表示上述平面区域的公共部分。(阴影部分)新会实验中学liang13练习:P111 题1,2,3,4分析 题1,选B直线l过(1,0),(0,1)
所以l的方程为y=-x+1,即x+y-1=0把(0,0)代入得0+0-1<0
所以原点在x+y-1<0所表示的区域。新会实验中学liang14分析 题2,解:先画出直线l:7x+2y-14=0,取原点O(0,0),把O点的坐标代入7x+2y-14,得 7×0-2×0-14=-14<0 所以,原点在不等式7x+2y-14<0所表示的平面区域内,不等式7x+2y-14<0所表示的平面区域如图阴影部分。新会实验中学liang15分析 题3如图所示:不等式①表示直线x+y≤500的左下方(包括直线)的平面区域;不等式②表示直线x=240的右(包括直线)的平面区域;不等式 ③表示直线x=180的上方(包括直线)的平面区域;阴影部分为所求xy-1O新会实验中学liang16作业:P121 A 1,2做在课本P111 练习1 第4题做在作业本
(1)能从实际情境中抽象出二元一次不等式组;
(2)了解二元一次不等式的几何意义;
(3)能用平面区域表示二元一次不等式组;新会实验中学liang2一名刚参加工作的大学生为自己制定的每月用餐费的最低标准是240元,又知其他费用最少需支出180元,而每月可用来支配的资金为500元,这名新员工可以如何使用这些钱?如:用餐费可不可以为300元,可不可以为
350元如:用餐费为280元时,其他费用可不可以
为200元新会实验中学liang3设用餐费为x元,其他费用为y元,由题意:X不小于240,y不小于180,x与y之和不超过500,用不等式组可表示为:不等式组的一个解(x,y)视为直角坐标系上的一个点,如(280,200)表示_______则问题转化为:确定平面直角坐标系中不等式组的解集区域新会实验中学liang4平面直角坐标系中,哪些点满足不等式 x>y作直线l:y=x在直线l两侧任意一点有什么特点:
右下方:
左上方:A(1,1)x>yx
试确定集合{(x,y)|x+2y-3>0}表示的平面区域分析:作直线 l:x+2y-3=0直线 l:x+2y-3=0把直角坐标平面分成三部分。新会实验中学liang8解:直线l将直角平面坐标系分成三部分(l及其两侧)。在l的右上方的平面区域内的任一点的坐标(x,y)满足不等式x+2y-3>0,而另外两部分的点均不满足不等式x+2y-3>0。不等式x+2y-3>0表示的是直线l右上方的平面区域新会实验中学liang9 一般地直线l:ax+by+c=0把直角坐标平面分成了三个部分: (1)直线l上的点(x,y)的坐标满足ax+by+c=0; (2)直线l一侧的平面区域内的点(x,y)的坐标满足ax+by+c>0; (3)直线l另一侧的平面区域内的点(x,y)的坐标满足ax+by+c<0; 只需在直线l的某一侧的平面区域内,任取一特殊点(x0,y0)(一般取原点(0,0)),从ax0+by0+c值的正负得出结论新会实验中学liang10【例2】 画出不等式2x-y-4≤0表示的平面区域。解:先画出直线l:2x-y-4=0,取原点O(0,0),把O点的坐标代入2x-y-4,得 2×0-0-4=-4<0 所以,原点在不等式2x-y-4<0所表示的平面区域内,不等式2x-y-4 ≤0所表示的平面区域是不等式2x-y-4<0所表示的平面区域加上直线l:2x-y-4=0新会实验中学liang11【例2】 画出以下不等式组表示的平面区域。分析:不等式组表示的平面区域是不等式①,
②,③所表示的平面区域的公共部分。新会实验中学liang12如图所示:不等式①表示直线x+y-1=0的右上方(包括直线)的平面区域;不等式②表示直线x-y=0的右下方(包括直线)的平面区域;不等式 ③表示直线x=2的左方(包括直线)的平面区域;所以,原不等式组表示上述平面区域的公共部分。(阴影部分)新会实验中学liang13练习:P111 题1,2,3,4分析 题1,选B直线l过(1,0),(0,1)
所以l的方程为y=-x+1,即x+y-1=0把(0,0)代入得0+0-1<0
所以原点在x+y-1<0所表示的区域。新会实验中学liang14分析 题2,解:先画出直线l:7x+2y-14=0,取原点O(0,0),把O点的坐标代入7x+2y-14,得 7×0-2×0-14=-14<0 所以,原点在不等式7x+2y-14<0所表示的平面区域内,不等式7x+2y-14<0所表示的平面区域如图阴影部分。新会实验中学liang15分析 题3如图所示:不等式①表示直线x+y≤500的左下方(包括直线)的平面区域;不等式②表示直线x=240的右(包括直线)的平面区域;不等式 ③表示直线x=180的上方(包括直线)的平面区域;阴影部分为所求xy-1O新会实验中学liang16作业:P121 A 1,2做在课本P111 练习1 第4题做在作业本
