5.3什么是几何证明课件

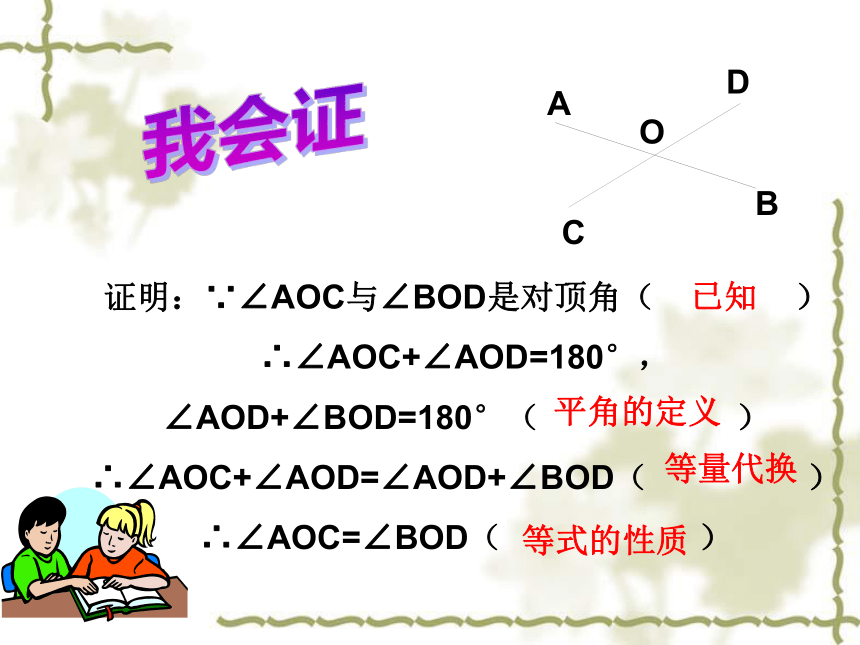
课件15张PPT。5.3什么是几何证明（1）豪迈中学 八年级数学预习检测1、经过长期实践总结出来，被大家所公认的（ ） 真命题定理叫做基本事实。2、经过推理得到证实的真命题叫做（ ）3、由已知条件出发，经过一步步的推理，最后证实结论正确的全部过程叫做（ ）。证明OACBD4、已知：如图，∠AOC与∠BOD是对顶角，
求证：∠AOC=∠BODOABDC证明：∵∠AOC与∠BOD是对顶角（ ）
∴∠AOC+∠AOD=180°，
∠AOD+∠BOD=180°（ ）
∴∠AOC+∠AOD=∠AOD+∠BOD（ ）
∴∠AOC=∠BOD（ ）
平角的定义等量代换已知等式的性质我会证命题有真命题与假命题之分想一想有一些命题是
人们经过长期实践后而公认为正确的命题叫基本事实基本事实有什么作用呢基本事实可以作为证实其他真命题的依据.1.两点确定一条直线.
2.两点之间线段最短
3.经过直线外一点有且只有一条直线与已知直线平行.
4.同位角相等, 两直线平行.
5.ASA; SAS; SSS.
6.全等三角形的对应边相等,对应角相等.
7.等式的基本性质.
8.不等式的基本性质.读一读本套教材选用如下命题作为基本事实 :在等式或不等式中,一个量可以用它的等量来代替.例如:如果a=b,b=c;那么a=c,这一性质也看作基本事实,称为“等量代换”.其它基本事实如何证明一个命题是真命题呢？能不能根据已经知道的真命题证实呢?那已经知道的真命题又是如何证实的?.想一想除基本事实外，命题的真实性都必须经过证明。推理的过程叫做证明基本事实通过推理的方法得到证实的真命题叫定理相信自己行，你就行！证一证两直线平行，同旁内角互补。已知：如图，直线a∥b，∠1和∠2是直线a、b被直线c所截得到的同旁内角。求证：∠1+∠2=180°证明：∵a∥b（ ）
∴∠3=∠2（ ）
又∵∠1+∠3=180°（ ）
∴∠1+∠2=180°（ ） cab312已知两直线平行，同位角相等补角的定义等量代换合作探究通过证明平行线的性质定理：两直线平行，同旁内角互补。你认为几何证明的步骤应分哪几步？在书写格式上应注意哪些问题？ 1、根据题意，画出图形。
2、结合图形，写出已知、求证。
3、写出证明过程。{步骤注意事项：1、图形中要标出必要的字母和符号。
2、已知、求证要用符号语言。
3、证明的每一步都要有依据。点拨例证：如图,△ABC是一个钢架，AB=AC，AD是连接点A与BC中点D的支架，
求证：△ABD≌△ACD。证明：∵点D是BC的中点（ ）
∴BD=CD（ ）
又∵AB=AC（ ）
AD=AD（ ）
∴△ABD≌△ACD（ ）已知线段中点的含义已知公共边SSS一个命题是否正确，需要经过理由充足，使人信服的推理论证才能得出结论，这样的推理过程叫做“证明”。观察、试验等是发现规律的重要途径，而证明则是确认规律的必要步骤。点拨：练一练:如图,若∠1+∠2=1800,则a∥b.用推理的方法说明它是一个真命题.已知：如图，∠1+∠2=180°求证：a∥b证明：∵∠1+∠2=180°（ ）
∠2+∠3=180°（ ）
∴∠1+ ∠2 = ∠2 +∠3（ ）
∴∠1= ∠3 （ ）
∴a∥b（ ） 已知补角的定义等式的基本性质同位角相等，两直线平行等量代换如图，已知：∠1=∠2，
求证：∠3=∠4拓展训练证明：∵∠1=∠2（ ）
∴l1∥l2 （ ）
∴∠3=∠4（ ）已知两直线平行，内错角相等同位角相等，两直线平行点拨：1、若给出的是命题，应该先画出图形写出已知和求证，再证明。
2、若已知、求证和图形已经给出，那就直接证明。本节课你学到什么？达标检测AEFBCDPQ1.在题中的括号内填写理由.已知：直线AB∥CD，直线EF与AB、
CD分别交于P和Q，AB⊥EF.求证：CD⊥EF证明：∵ AB∥CD（ ）
∴∠EPB=∠PQD（ ）
又∵ AB⊥EF（ ）
∴∠EPB=90°（ ）
∴∠PQD=90°（ ）
∴ CD⊥EF（ ）已知两直线平行，同位角相等已知垂线的定义等量代换垂线的定义2、已知：如图，直线a∥b，
求证：∠1=∠3ab123第2题图第1题图