简单几何体
图片预览


文档简介
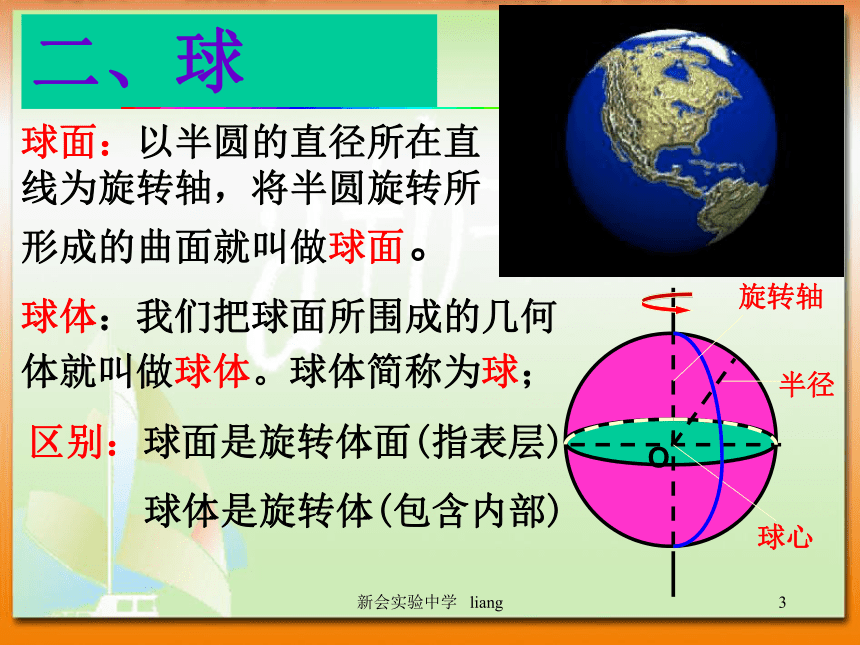
课件25张PPT。新会实验中学 liang1§1.1.1简单几何体新会实验中学 liang1一、引入问题:什么是数学?答:数学是研究客观物质世界的数量关系和空间形式的一门科学。初中阶段的代数、高中阶段的函数,主要是研究数量关系初中的平面几何、高中的立体几何,主要是研究空间形式新会实验中学 liang1二、球球面:以半圆的直径所在直线为旋转轴,将半圆旋转所形成的曲面就叫做球面。 球体:我们把球面所围成的几何体就叫做球体。球体简称为球; 区别:球面是旋转体面(指表层)
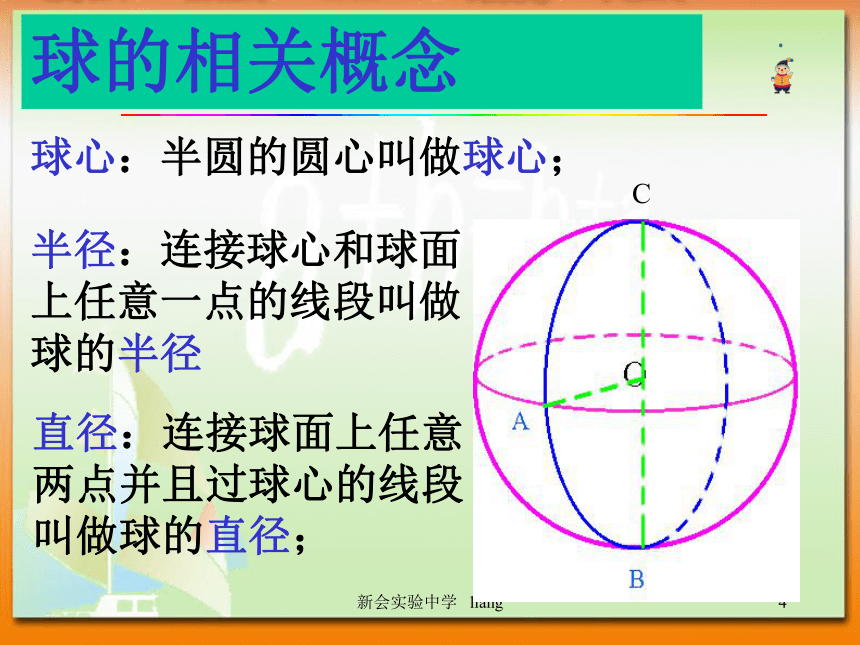
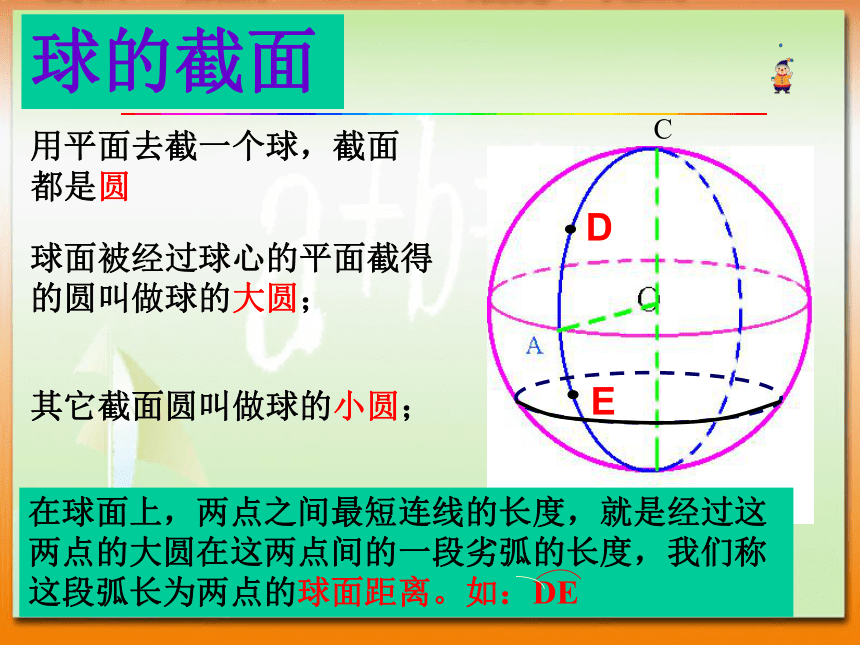
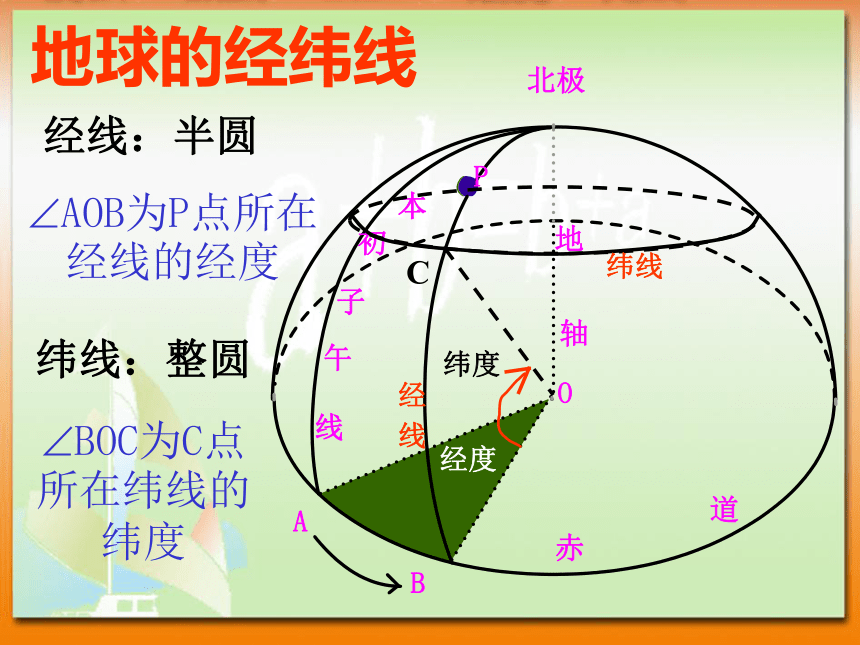
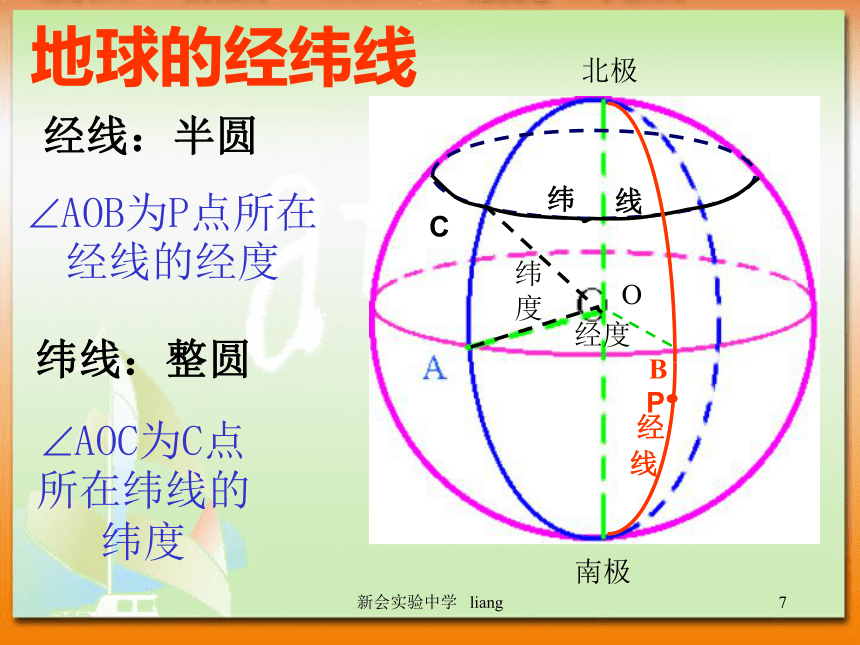
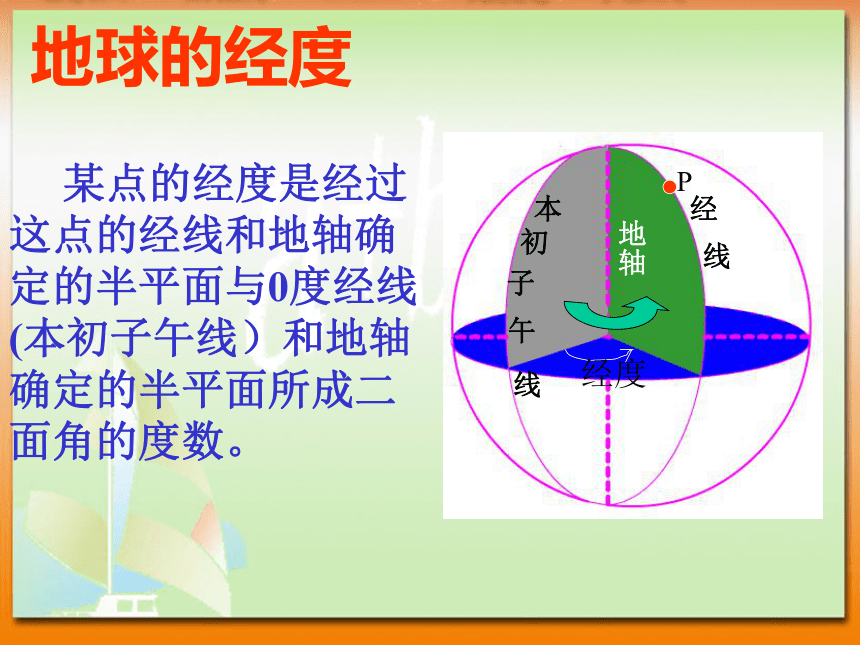
球体是旋转体(包含内部) 新会实验中学 liang1半径:连接球心和球面上任意一点的线段叫做球的半径直径:连接球面上任意两点并且过球心的线段叫做球的直径;球心:半圆的圆心叫做球心;球的相关概念新会实验中学 liang1用平面去截一个球,截面都是圆球的截面球面被经过球心的平面截得的圆叫做球的大圆;其它截面圆叫做球的小圆;在球面上,两点之间最短连线的长度,就是经过这两点的大圆在这两点间的一段劣弧的长度,我们称这段弧长为两点的球面距离。如:DEDE?AOB为P点所在经线的经度经线:半圆纬线:整圆?BOC为C点所在纬线的纬度地球的经纬线新会实验中学 liang1?AOB为P点所在经线的经度经线:半圆纬线:整圆?AOC为C点所在纬线的纬度地球的经纬线地球的经度 某点的经度是经过这点的经线和地轴确定的半平面与0度经线(本初子午线)和地轴确定的半平面所成二面角的度数。经度?AOP为 P点
所在纬线的
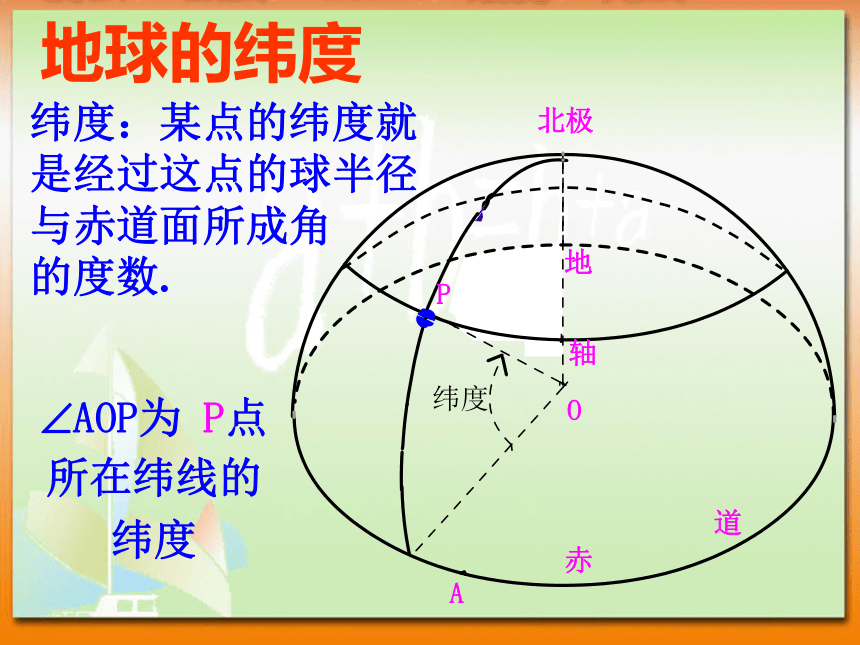
纬度纬度:某点的纬度就是经过这点的球半径与赤道面所成角
的度数.地球的纬度新会实验中学 liang1地理知识新会实验中学 liang1三、圆柱、圆锥、圆台相关概念:高、底面、侧面、母线、旋转面、旋转体;新会实验中学 liang1B’柱、锥、台、球的结构特征AA’OBO’结构特征 以矩形的一边所在直线为旋转轴,其余边旋转形成的曲面所围成的几何体叫做圆柱。相关概念:高、底面、侧面、母线、旋转面、旋转体;圆柱新会实验中学 liang1柱、锥、台、球的结构特征SABO结构特征 以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫做圆锥。圆锥新会实验中学 liang1柱、锥、台、球的结构特征结构特征 用一个平行于圆锥底面的平面去截圆锥,底面与截面之间的部分是圆台.圆台新会实验中学 liang1四、棱柱、棱锥、棱台相关概念(见课本P5—P6)注:被遮住的部分必需要用虚线新会实验中学 liang1柱、锥、台、球的结构特征结构特征 有两个面互相平行,其余各面都是四边形,并且每相邻两个面的公共边都平行。(1)底面互相平行。
(2)侧面是平行四边形。棱柱新会实验中学 liang1分类一:
斜棱柱:侧棱不垂直于底面的棱柱;
直棱柱:侧棱垂直于底面的棱柱;
正棱柱:底面是正多边形的直棱柱. 分类二:
棱柱的底面可以是三角形、四角形、五角形……我们把这样的棱柱分别叫作三棱柱、四棱柱、五棱柱……新会实验中学 liang1柱、锥、台、球的结构特征SABCD结构特征 有一个面是多边形,其余各面都是有一个公共顶点的三角形。棱锥正棱锥:如果棱锥的底面是正多边形,且各侧面全等.
正棱柱的侧面是全等的等腰三角形,它底边上的高叫作正棱柱的斜高新会实验中学 liang1柱、锥、台、球的结构特征结构特征 用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分是棱台.棱台正棱台:用正棱锥截得的棱台.正棱台的侧面是全等的等腰梯形,它的高叫作正棱台的斜高.新会实验中学 liang1②斜棱柱的侧面中可能有矩形吗?答:分别是:圆、矩形、等腰三角形、等腰梯形;答:可能有矩形; 新会实验中学 liang1③图中的几何体是棱台吗?新会实验中学 liang12、画出下列图形 ①棱长为3cm的正方体;②底边长为3cm,高为3cm的正四棱锥;新会实验中学 liang1③半径为2cm的球;注:遮住的部分必需要用虚线④底半径为2cm,高为4cm的圆锥;新会实验中学 liang1七、课堂小结②掌握常见的立体几何图形的画法;①了解旋转体、多面体、球、柱、锥、台等相关概念;③了解地球的经纬度。新会实验中学 liang1 八、课后作业分别画出下列四个图形 ①棱长为3cm的正方体;②底边长为3cm,高为3cm的正四棱锥;③半径为2cm的球;④底半径为2cm,高为4cm的圆锥。
球体是旋转体(包含内部) 新会实验中学 liang1半径:连接球心和球面上任意一点的线段叫做球的半径直径:连接球面上任意两点并且过球心的线段叫做球的直径;球心:半圆的圆心叫做球心;球的相关概念新会实验中学 liang1用平面去截一个球,截面都是圆球的截面球面被经过球心的平面截得的圆叫做球的大圆;其它截面圆叫做球的小圆;在球面上,两点之间最短连线的长度,就是经过这两点的大圆在这两点间的一段劣弧的长度,我们称这段弧长为两点的球面距离。如:DEDE?AOB为P点所在经线的经度经线:半圆纬线:整圆?BOC为C点所在纬线的纬度地球的经纬线新会实验中学 liang1?AOB为P点所在经线的经度经线:半圆纬线:整圆?AOC为C点所在纬线的纬度地球的经纬线地球的经度 某点的经度是经过这点的经线和地轴确定的半平面与0度经线(本初子午线)和地轴确定的半平面所成二面角的度数。经度?AOP为 P点
所在纬线的
纬度纬度:某点的纬度就是经过这点的球半径与赤道面所成角
的度数.地球的纬度新会实验中学 liang1地理知识新会实验中学 liang1三、圆柱、圆锥、圆台相关概念:高、底面、侧面、母线、旋转面、旋转体;新会实验中学 liang1B’柱、锥、台、球的结构特征AA’OBO’结构特征 以矩形的一边所在直线为旋转轴,其余边旋转形成的曲面所围成的几何体叫做圆柱。相关概念:高、底面、侧面、母线、旋转面、旋转体;圆柱新会实验中学 liang1柱、锥、台、球的结构特征SABO结构特征 以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫做圆锥。圆锥新会实验中学 liang1柱、锥、台、球的结构特征结构特征 用一个平行于圆锥底面的平面去截圆锥,底面与截面之间的部分是圆台.圆台新会实验中学 liang1四、棱柱、棱锥、棱台相关概念(见课本P5—P6)注:被遮住的部分必需要用虚线新会实验中学 liang1柱、锥、台、球的结构特征结构特征 有两个面互相平行,其余各面都是四边形,并且每相邻两个面的公共边都平行。(1)底面互相平行。
(2)侧面是平行四边形。棱柱新会实验中学 liang1分类一:
斜棱柱:侧棱不垂直于底面的棱柱;
直棱柱:侧棱垂直于底面的棱柱;
正棱柱:底面是正多边形的直棱柱. 分类二:
棱柱的底面可以是三角形、四角形、五角形……我们把这样的棱柱分别叫作三棱柱、四棱柱、五棱柱……新会实验中学 liang1柱、锥、台、球的结构特征SABCD结构特征 有一个面是多边形,其余各面都是有一个公共顶点的三角形。棱锥正棱锥:如果棱锥的底面是正多边形,且各侧面全等.
正棱柱的侧面是全等的等腰三角形,它底边上的高叫作正棱柱的斜高新会实验中学 liang1柱、锥、台、球的结构特征结构特征 用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分是棱台.棱台正棱台:用正棱锥截得的棱台.正棱台的侧面是全等的等腰梯形,它的高叫作正棱台的斜高.新会实验中学 liang1②斜棱柱的侧面中可能有矩形吗?答:分别是:圆、矩形、等腰三角形、等腰梯形;答:可能有矩形; 新会实验中学 liang1③图中的几何体是棱台吗?新会实验中学 liang12、画出下列图形 ①棱长为3cm的正方体;②底边长为3cm,高为3cm的正四棱锥;新会实验中学 liang1③半径为2cm的球;注:遮住的部分必需要用虚线④底半径为2cm,高为4cm的圆锥;新会实验中学 liang1七、课堂小结②掌握常见的立体几何图形的画法;①了解旋转体、多面体、球、柱、锥、台等相关概念;③了解地球的经纬度。新会实验中学 liang1 八、课后作业分别画出下列四个图形 ①棱长为3cm的正方体;②底边长为3cm,高为3cm的正四棱锥;③半径为2cm的球;④底半径为2cm,高为4cm的圆锥。
