人教版五年级上册数学第六单元多边形的面积 三角形的面积变式练习(课件)(共16张PPT)
文档属性
| 名称 | 人教版五年级上册数学第六单元多边形的面积 三角形的面积变式练习(课件)(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 992.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-18 12:37:48 | ||
图片预览



文档简介
(共16张PPT)
三角形的面积
变式练习
同学们,我们已经学习过三角形的面积推导和计算,三角形的面积你会计算吗?
一、温故而知新
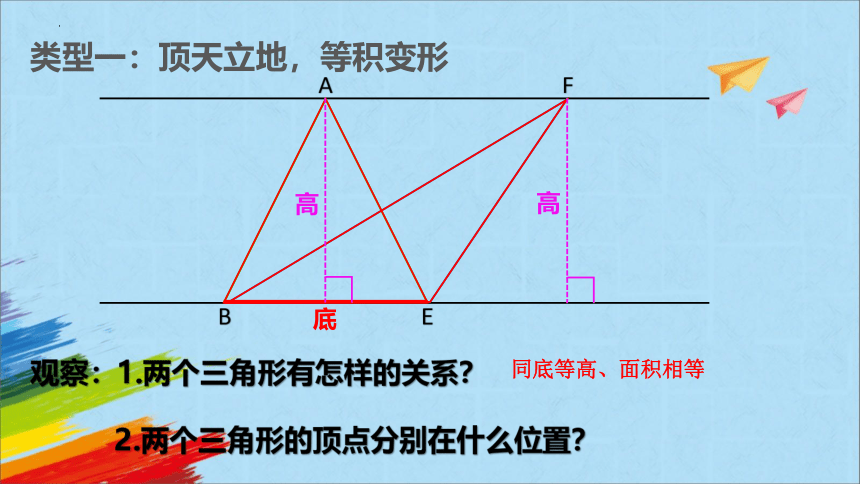
观察:1.两个三角形有怎样的关系?
A
F
B
E
类型一:顶天立地,等积变形
底
高
高
2.两个三角形的顶点分别在什么位置?
同底等高、面积相等
类型一:顶天立地 等积变形
步骤:
1.寻找平行线(天和地)
2.在其中一条线上寻找三角形的底(地)
3.底(地)不动,移动天上的顶点
4.面积相等,变形成功
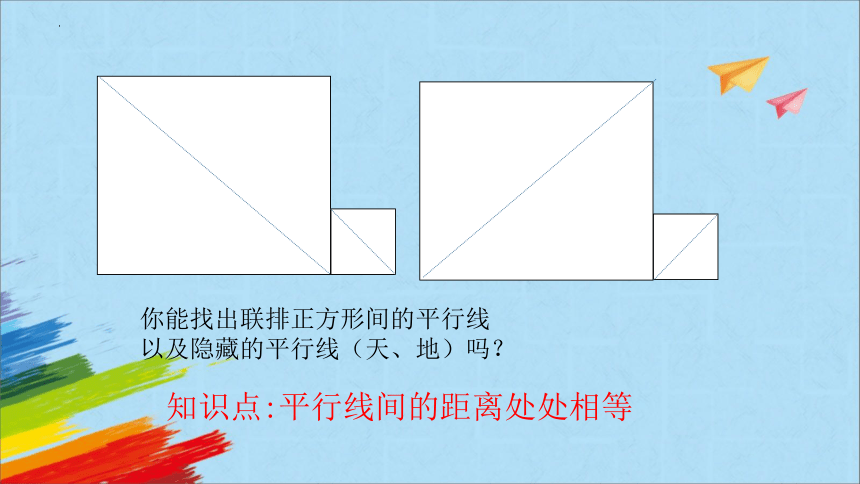
你能找出联排正方形间的平行线
以及隐藏的平行线(天、地)吗?
知识点:平行线间的距离处处相等
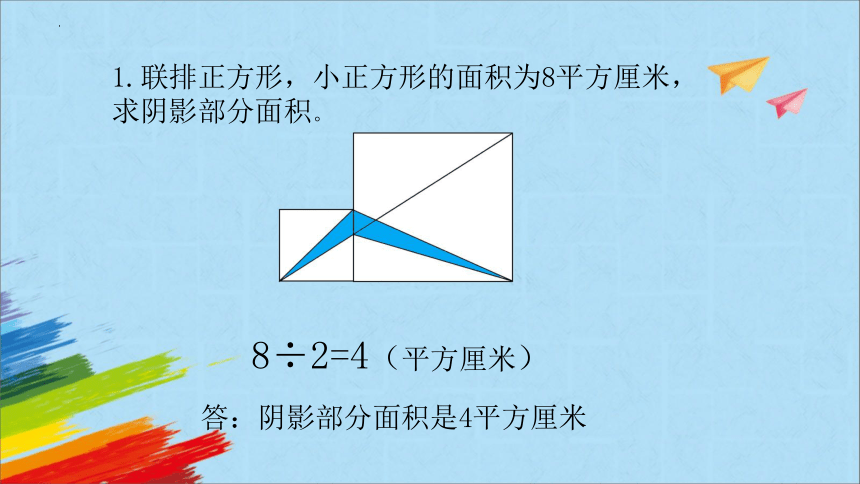
1.联排正方形,小正方形的面积为8平方厘米,求阴影部分面积。
8÷2=4(平方厘米)
答:阴影部分面积是4平方厘米
A
B
D
E
F
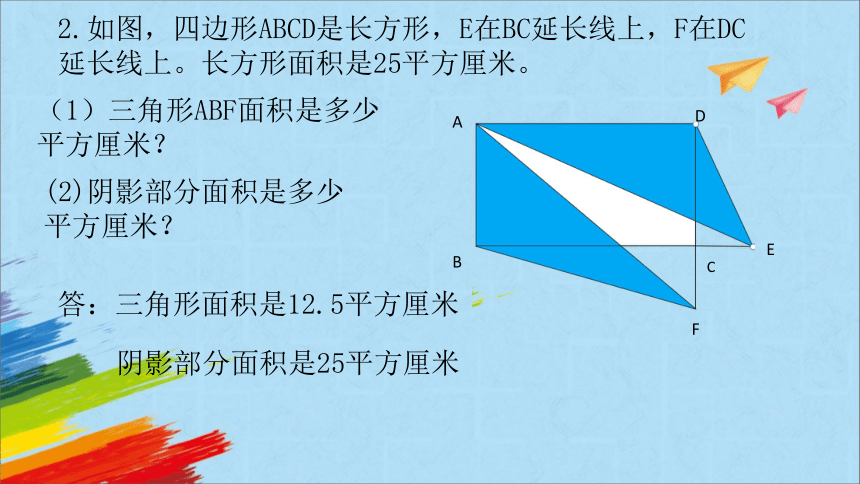
2.如图,四边形ABCD是长方形,E在BC延长线上,F在DC延长线上。长方形面积是25平方厘米。
答:三角形面积是12.5平方厘米
(1)三角形ABF面积是多少平方厘米?
(2)阴影部分面积是多少平方厘米?
C
阴影部分面积是25平方厘米
1.两个底是8厘米,高是6厘米的三角形,重叠在一起,重叠部分面积是8平方厘米.这个图形所能覆盖的面积是多少?
思路:两个三角形面积和-重叠部分面积=图形所覆盖面积
类型二:容斥原理
1.旧知重现:在一次校运动会上,502班参加田赛有25人,参加径赛的有28人,既参加田赛又参加径赛的有11人,502班一共有多少人?
既参加田赛也参加径赛的人
只参加田赛的人
只参加径赛的人
25+28-11=42(人)
答:502班一共有42人。
1.两个底是8厘米,高是6厘米的三角形,重叠在一起,重叠部分面积是8平方厘米.这个图形所能覆盖的面积是多少?
解:两个三角形面积:
8×6÷2×2=48(平方厘米)
减去重复部分:48-8=40(平方厘米)
思路:两个三角形面积和-重复部分面积=图形所覆盖面积
在计数时,为了使重叠部分不被重复计算,人们研究出了一种新的计数方法—容斥原理
基本思想:
1、先不考虑重叠情况,把包含于某内容中的 所有对象的数目先计算出来,
2、再把计数时重复计数的数目排斥出去
3、计算结果无遗漏无重复
(思维提升)如下图,在长方形ABCD中,AD=15厘米,AB=8厘米,四边形OEFG的面积是9平方厘米。求阴影部分面积是多少?
三角形AFC面积=CF×AB÷2
三角形BDF面积=BF×AB÷2
三角形AFC面积+三角形AFC面积=CF×AB÷2+BF×AB÷2
=(CF+BF)×BF÷2
=BC×BF÷2
=8×15÷2
=60(平方厘米)
减去重复部分:60-9=51(平方厘米)
阴影部分面积=长方形面积-51
=15×8- 51
=69(平方厘米)
方法一:容斥原理
方法二:等级变形+容斥原理
8×15÷2=60(平方厘米)
60-9=51(平方厘米)
多加了一份重叠部分面积,应减去
空白部分面积
阴影部分面积:8×15-51=69(平方厘米)
三、课堂小结
通过本堂课的学习,你有什么收获?
“流水不腐,户枢不蠹”
感谢各位教师的聆听!
三角形的面积
变式练习
同学们,我们已经学习过三角形的面积推导和计算,三角形的面积你会计算吗?
一、温故而知新
观察:1.两个三角形有怎样的关系?
A
F
B
E
类型一:顶天立地,等积变形
底
高
高
2.两个三角形的顶点分别在什么位置?
同底等高、面积相等
类型一:顶天立地 等积变形
步骤:
1.寻找平行线(天和地)
2.在其中一条线上寻找三角形的底(地)
3.底(地)不动,移动天上的顶点
4.面积相等,变形成功
你能找出联排正方形间的平行线
以及隐藏的平行线(天、地)吗?
知识点:平行线间的距离处处相等
1.联排正方形,小正方形的面积为8平方厘米,求阴影部分面积。
8÷2=4(平方厘米)
答:阴影部分面积是4平方厘米
A
B
D
E
F
2.如图,四边形ABCD是长方形,E在BC延长线上,F在DC延长线上。长方形面积是25平方厘米。
答:三角形面积是12.5平方厘米
(1)三角形ABF面积是多少平方厘米?
(2)阴影部分面积是多少平方厘米?
C
阴影部分面积是25平方厘米
1.两个底是8厘米,高是6厘米的三角形,重叠在一起,重叠部分面积是8平方厘米.这个图形所能覆盖的面积是多少?
思路:两个三角形面积和-重叠部分面积=图形所覆盖面积
类型二:容斥原理
1.旧知重现:在一次校运动会上,502班参加田赛有25人,参加径赛的有28人,既参加田赛又参加径赛的有11人,502班一共有多少人?
既参加田赛也参加径赛的人
只参加田赛的人
只参加径赛的人
25+28-11=42(人)
答:502班一共有42人。
1.两个底是8厘米,高是6厘米的三角形,重叠在一起,重叠部分面积是8平方厘米.这个图形所能覆盖的面积是多少?
解:两个三角形面积:
8×6÷2×2=48(平方厘米)
减去重复部分:48-8=40(平方厘米)
思路:两个三角形面积和-重复部分面积=图形所覆盖面积
在计数时,为了使重叠部分不被重复计算,人们研究出了一种新的计数方法—容斥原理
基本思想:
1、先不考虑重叠情况,把包含于某内容中的 所有对象的数目先计算出来,
2、再把计数时重复计数的数目排斥出去
3、计算结果无遗漏无重复
(思维提升)如下图,在长方形ABCD中,AD=15厘米,AB=8厘米,四边形OEFG的面积是9平方厘米。求阴影部分面积是多少?
三角形AFC面积=CF×AB÷2
三角形BDF面积=BF×AB÷2
三角形AFC面积+三角形AFC面积=CF×AB÷2+BF×AB÷2
=(CF+BF)×BF÷2
=BC×BF÷2
=8×15÷2
=60(平方厘米)
减去重复部分:60-9=51(平方厘米)
阴影部分面积=长方形面积-51
=15×8- 51
=69(平方厘米)
方法一:容斥原理
方法二:等级变形+容斥原理
8×15÷2=60(平方厘米)
60-9=51(平方厘米)
多加了一份重叠部分面积,应减去
空白部分面积
阴影部分面积:8×15-51=69(平方厘米)
三、课堂小结
通过本堂课的学习,你有什么收获?
“流水不腐,户枢不蠹”
感谢各位教师的聆听!
