2023-2024学年湖南省怀化市鹤城区雅礼实验学校八年级(上)入学数学试卷(含解析)
文档属性
| 名称 | 2023-2024学年湖南省怀化市鹤城区雅礼实验学校八年级(上)入学数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 320.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-18 18:07:57 | ||
图片预览




文档简介
2023-2024学年湖南省怀化市鹤城区雅礼实验学校八年级(上)入学数学试卷
一、选择题(本大题共10小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
1. “认识交通标志,遵守交通规则”,下列交通标志中,是轴对称图形的是( )
A. B. C. D.
2. 下列运算正确的是( )
A. B.
C. D.
3. 若是方程的一个解,那么的值是( )
A. B. C. D.
4. 若且,,则的值为( )
A. B. C. D.
5. 解方程组的最佳方法是( )
A. 代入法消去,由得 B. 代入法消去,由得
C. 加减法消去,得 D. 加减法消去,得
6. 小明参加演讲比赛的得分情况如表:
服装 普通话 主题
得分
评总分时,按服装占,普通话占,主题占,她的总得分是( )
A. B. C. D.
7. 如图,已知直线,,,则的高是.( )
A. B. C. D.
8. 下列说法:其中正确的说法有( )
相等的角是对顶角;
过一点有且只有一条直线与已知直线垂直;
平行于同一条直线的两条直线互相平行;
同角或等角的余角相等.
A. 个 B. 个 C. 个 D. 个
9. 已知,则的值为( )
A. B. C. D.
10. 如图,,为上方一点,、分别为、上的点,、的角平分线交于点,的角平分线与的延长线交于点,下列结论:
;
;
;
若,则.
其中正确的结论有个.( )
A. B. C. D.
二、填空题(本大题共6小题,共24.0分)
11. 计算: ______ .
12. 在数据、、、、、、中,众数是,那么这组数据的中位数是______ .
13. 已知直线,与之间的距离为,与之间有一点,点到的距离是,则点到的距离是______.
14. 已知,某学生将一直角三角板放置如图所示,如果,那么的度数为______.
15. 若是完全平方式,则的值为______.
16. 已知,则代数式的值是______.
三、计算题(本大题共1小题,共8.0分)
17. 因式分解:
.
四、解答题(本大题共7小题,共78.0分。解答应写出文字说明,证明过程或演算步骤)
18. 本小题分
解二元一次方程组:
;
.
19. 本小题分
先化简,再求值:,其中,.
20. 本小题分
已知:如图,点在直线上,点在直线上,,求证:.
21. 本小题分
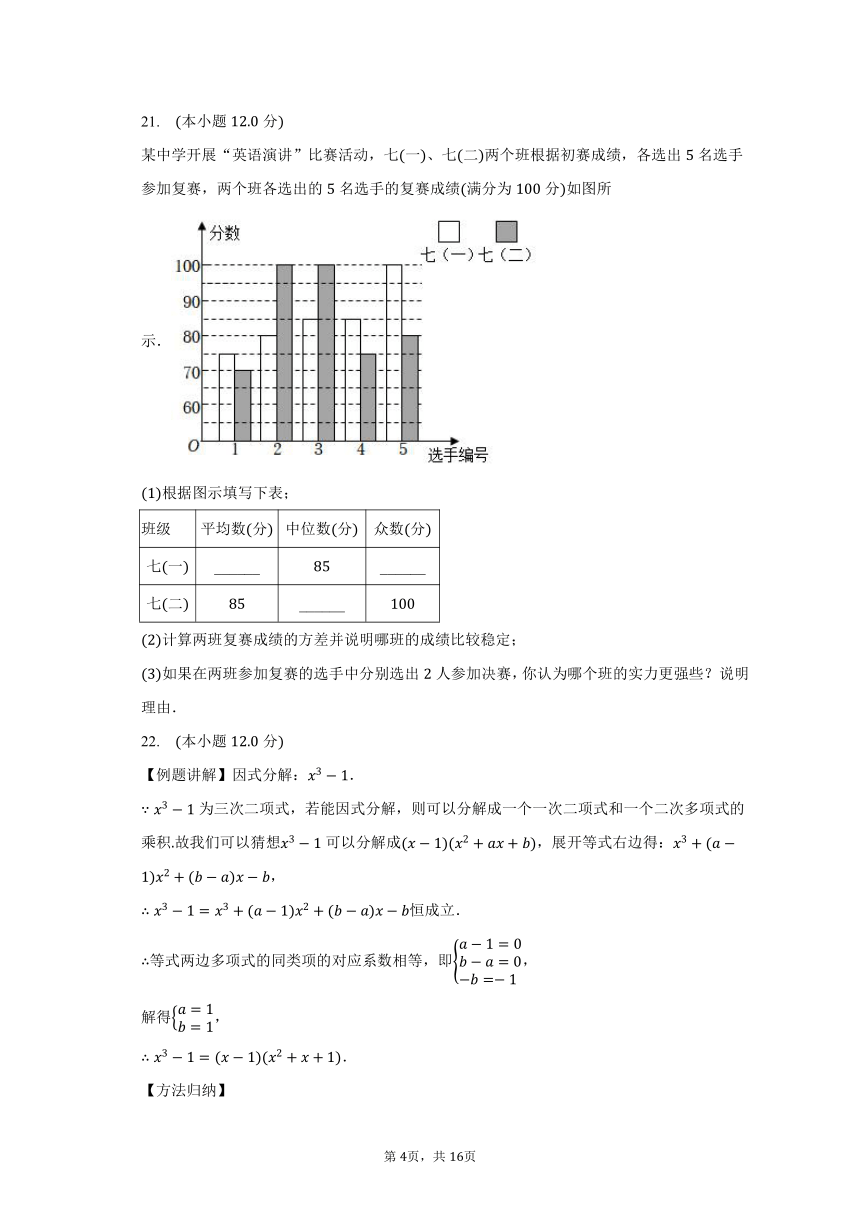
某中学开展“英语演讲”比赛活动,七一、七二两个班根据初赛成绩,各选出名选手参加复赛,两个班各选出的名选手的复赛成绩满分为分如图所示.
根据图示填写下表;
班级 平均数分 中位数分 众数分
七一 ______ ______
七二 ______
计算两班复赛成绩的方差并说明哪班的成绩比较稳定;
如果在两班参加复赛的选手中分别选出人参加决赛,你认为哪个班的实力更强些?说明理由.
22. 本小题分
【例题讲解】因式分解:.
为三次二项式,若能因式分解,则可以分解成一个一次二项式和一个二次多项式的乘积故我们可以猜想可以分解成,展开等式右边得:,
恒成立.
等式两边多项式的同类项的对应系数相等,即,
解得,
.
【方法归纳】
设某一多项式的全部或部分系数为未知数,利用当两个多项式为恒等式时,同类项系数相等的原理确定这些系数,从而得到待求的值,这种方法叫待定系数法.
【学以致用】
若,则 ______ ;
若有一个因式是,求的值及另一个因式.
23. 本小题分
在疫情防控期间,某中学为保障广大师生生命健康安全,预从商场购进一批免洗手消毒液和消毒液如果购买瓶免洗手消毒液和瓶消毒液,共需花费元,如果购买瓶免洗手消毒液和瓶消毒液,共需花费元.
每瓶免洗手消毒液和每瓶消毒液的价格分别是多少元?
若商场有两种促销方案:方案一,所有购买商品均打八折;方案二,购买瓶免洗手消毒液送瓶消毒液,学校打算购进免洗手消毒液瓶,消毒液瓶,请问学校选用哪种方案更节约钱?节约多少钱?
24. 本小题分
如图,,点为直线上一定点,为直线上的动点,在直线与之间且在线段的右方作点,使得设为锐角.
求与的和;提示过点作
当点在直线上运动时,试说明;
当点在直线上运动的过程中,若平分,也恰好平分,请求出此时的值
答案和解析
1.【答案】
【解析】解:、不是轴对称图形,故本选项错误;
B、是轴对称图形,故本选项正确;
C、不是轴对称图形,故本选项错误;
D、不是轴对称图形,故本选项错误;
故选:.
根据轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,进行判断即可.
本题考查了轴对称图形的知识,属于基础题,掌握轴对称的定义是关键.
2.【答案】
【解析】解:,故选项A正确,
,故选项B错误,
,故选项C错误,
,故选项D错误,
故选:.
根据各个选项中的式子可以计算出正确的结果,从而可以解答本题.
本题考查整式的混合运算,解答本题的关键是明确整式的混合运算的计算方法.
3.【答案】
【解析】解:将代入原方程得:,
解得:,
的值为.
故选:.
将代入原方程,可得出关于的一元一次方程,解之即可求出的值.
本题考查了二元一次方程的解,牢记“一般地,使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解”是解题的关键.
4.【答案】
【解析】解:,
故选:.
根据是正整数可得,然后再根据是正整数可得,然后再代入计算即可.
此题主要考查了幂的乘方,以及同底数幂的乘法,关键是掌握幂的乘方法则:底数不变,指数相乘.同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加.
5.【答案】
【解析】【分析】
此题考查了解二元一次方程组,以及解一元一次方程,熟练掌握运算法则是解本题的关键.利用加减消元法判断即可.
【解答】
解方程组的最佳方法是加减法消去,得,
故选:.
6.【答案】
【解析】解:她的总得分是:.
故选:.
根据加权平均数的计算公式进行计算即可.
本题考查的是加权平均数,熟记加权平均数的计算公式是解决本题的关键.
7.【答案】
【解析】解:设的边上的高为.
,
,
,
.
故选:.
设的边上的高为构建方程求解.
本题考查三角形的面积,平行线的性质等知识,解题的关键是掌握等高模型,学会利用参数解决问题.
8.【答案】
【解析】解:相等的角不一定是对顶角,原命题是假命题;
在同一平面上,过一点有且只有一条直线与已知直线垂直,原命题是假命题;
平行于同一条直线的两条直线互相平行,是真命题;
同角或等角的余角相等,是真命题;
故选:.
根据对顶角、平行线的判定、等角的余角和垂直的判定进行判断即可.
此题考查平行线的判定和性质,关键是根据对顶角、平行线的判定、等角的余角和垂直的判定解答.
9.【答案】
【解析】解:,
,
得:,即,
将代入得:,即,
则原式.
故选C.
利用非负数的性质列出关于与的方程组,求出方程组的解得到与的值,即可求出所求式子的值.
此题考查了解二元一次方程组,以及非负数的性质,利用了消元的思想,消元的方法有:加减消元法与代入消元法.
10.【答案】
【解析】解:平分,平分,
,,
,
即,故正确;
设与交于,于交于,
,
,
,
,故正确;
平分,平分,
,,
,
,,
,
,,
,故正确;
,,
,
,
,
,
,
,
,
解得,
,故正确.
综上,正确答案有个,
故选:.
由角平分线的定义及平行线的性质可求解,即可判定;设与交于,于交于,由平行线的性质可得,结合三角形外角的性质可性质;由角平分线的定义可得,,结合平行线的性质可得,再利用三角形外角的性质可证明;由三角形外角的性质可得,根据直角三角形的性质及的结论可求解的度数,即可判定.
本题主要考查平行线的性质,角平分线的定义,三角形外角的性质,灵活运用性质解决问题是解题的关键.
11.【答案】
【解析】解:原式
.
故答案为:.
根据积的乘方计算即可.
本题考查幂的乘方与积的乘方,掌握运算法则是解题的关键.
12.【答案】
【解析】解:数据、、、、、、中,众数是,
,
这组数据按照从小到大排列是:、、、、、、,
这组数据的中位数是,
故答案为:.
根据数据、、、、、、中,众数是,可以得到的值,然后将数据按照从小到大排列,即可得到这组数据的中位数.
本题考查众数和中位数,解答本题的关键是明确题意,利用众数和中位数的知识解答.
13.【答案】
【解析】解:直线,与之间的距离为,与之间有一点,点到的距离是,
点到的距离是,
故答案为:.
根据直线,与之间的距离为,与之间有一点,点到的距离是,即可得出点到的距离.
本题主要考查了平行线之间的距离,从一条平行线上的任意一点到另一条直线作垂线,垂线段的长度叫两条平行线之间的距离.
14.【答案】
【解析】解:如图所示:
,
,
,
,
,且,
,
,
故答案为:.
利用两直线平行同位角相等得到一对角相等,再由对顶角相等及直角三角形两锐角互余求出所求角度数即可.
此题考查了平行线的性质、对顶角相等的性质、直角三角形的性质,熟练掌握平行线的性质是解本题的关键.
15.【答案】或
【解析】本题考查完全平方公式,解题的关键是熟练运用完全平方公式,本题属于基础题型.
根据完全平方公式即可求出答案.
解:,
,
或.
故答案为:或.
16.【答案】
【解析】解:,
,
故答案为:
利用完全平方公式计算即可求出值所求.
此题考查了完全平方公式,熟练掌握公式是解本题的关键.
17.【答案】解:;
.
【解析】原式提取公因式即可得到结果;
原式利用平方差公式,以及完全平方公式分解即可.
此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.
18.【答案】解:,
,得,
解得,
将代入,得,
解得,
原方程组的解为;
,
由得,,
由得,
,得,
解得,
将代入,得,
解得,
原方程组的解为.
【解析】根据加减消元法解二元一次方程组即可;
根据加减消元法解二元一次方程组即可.
本题考查了解二元一次方程组,熟练掌握解二元一次方程组的方法是解题的关键.
19.【答案】解:原式
,
把, 代入上式,原式.
【解析】先根据乘法公式算乘法,再合并同类项,最后求出答案即可.
本题考查了整式的混合运算和求值,能正确根据整式的运算法则进行化简是解此题的关键.
20.【答案】证明:,,
,
同位角相等,两直线平行,
,
,
,
同旁内角互补,两直线平行,
.
【解析】先根据题意得出,再由得出,故可得出,进而可得出结论.
本题考查的是平行线的判定与性质,熟知平行线的判定定理是解答此题的关键.
21.【答案】
【解析】解:由图可知七一班名选手的复赛成绩为:、、、、,七二班名选手的复赛成绩为:、、、、,
七一班的成绩的平均分是,
出现次数最多的是,则七一班的成绩的众数是;
七二班的成绩按从小到大的顺序排列,第位是,即七二班的中位数是.
填表:
班级 平均数分 中位数分 众数分
七一
七二
七一班的成绩比较稳定.理由如下:
,
,
,
七一班的成绩比较稳定;
七二班的实力更强些.理由如下:
七一班复赛成绩较好的前两名选手的成绩分别为,,
七二班复赛成绩较好的前两名选手的成绩分别为,,
在每班参加复赛的选手中分别选出人参加决赛,七二班的实力更强些.
观察图分别写出七一班和七二班名选手的复赛成绩,然后根据中位数的定义和平均数的求法以及众数的定义求解即可;
先根据方差公式分别计算两个班复赛成绩的方差,再根据方差的意义判断即可;
分别计算前两名的平均分,比较其大小.
本题考查了平均数、中位数、众数和方差的意义即运用.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定
22.【答案】
【解析】解:,
,
,
,
故答案为:;
设另一个因式为,
,
,
,,
解得,,
另一个因式为.
根据题目中的待定系数法原理即可求得结果;
根据待定系数法原理先设另一个多项式,然后根据恒等原理即可求得结论.
本题考查了因式分解的应用、多项式乘以多项式,解决本题的关键是理解并会运用待定系数法原理.
23.【答案】解:设每瓶免洗手消毒液价格是元,每瓶消毒液的价格是元,
由题意得:,
解得:,
每瓶免洗手消毒液价格是元,每瓶消毒液的价格是元,
答:每瓶免洗手消毒液价格是元,每瓶消毒液的价格是元;
方案一的花费为:元,
方案二的花费为:元,
,
方案一更节约钱,
节约钱为:元,
答:学校选用方案一更节约钱,节约元.
【解析】设每瓶免洗手消毒液价格是元,每瓶消毒液的价格是元,由“如果购买瓶免洗手消毒液和瓶消毒液,共需花费元,如果购买瓶免洗手消毒液和瓶消毒液,共需花费元”,列出二元一次方程组,解方程组即可;
分别求出方案一和方案二的花费情况,然后比较大小并作差即可.
本题考查了二元一次方程组的应用,找准等量关系,列出二元一次方程组是解题的关键.
24.【答案】解:如图,过点作,则.
,,
.
,
.
,
,
.
由得:,则.
,
,
.
若平分,也恰好平分,
则有,,.
,
,
.
由知:,
则,
解得:.
【解析】过点作,则,,依据平行线的性质可得到,则,最后,依据垂线的定义求解即可;
由得,然后结合,进行证明即可;
先求得的度数用含的式子表示,然后再利用中的结论列方程求解即可.
本题主要考查的是平行线的性质和判定,熟练掌握平行线的性质定理是解题的关键.
第1页,共1页
一、选择题(本大题共10小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
1. “认识交通标志,遵守交通规则”,下列交通标志中,是轴对称图形的是( )
A. B. C. D.
2. 下列运算正确的是( )
A. B.
C. D.
3. 若是方程的一个解,那么的值是( )
A. B. C. D.
4. 若且,,则的值为( )
A. B. C. D.
5. 解方程组的最佳方法是( )
A. 代入法消去,由得 B. 代入法消去,由得
C. 加减法消去,得 D. 加减法消去,得
6. 小明参加演讲比赛的得分情况如表:
服装 普通话 主题
得分
评总分时,按服装占,普通话占,主题占,她的总得分是( )
A. B. C. D.
7. 如图,已知直线,,,则的高是.( )
A. B. C. D.
8. 下列说法:其中正确的说法有( )
相等的角是对顶角;
过一点有且只有一条直线与已知直线垂直;
平行于同一条直线的两条直线互相平行;
同角或等角的余角相等.
A. 个 B. 个 C. 个 D. 个
9. 已知,则的值为( )
A. B. C. D.
10. 如图,,为上方一点,、分别为、上的点,、的角平分线交于点,的角平分线与的延长线交于点,下列结论:
;
;
;
若,则.
其中正确的结论有个.( )
A. B. C. D.
二、填空题(本大题共6小题,共24.0分)
11. 计算: ______ .
12. 在数据、、、、、、中,众数是,那么这组数据的中位数是______ .
13. 已知直线,与之间的距离为,与之间有一点,点到的距离是,则点到的距离是______.
14. 已知,某学生将一直角三角板放置如图所示,如果,那么的度数为______.
15. 若是完全平方式,则的值为______.
16. 已知,则代数式的值是______.
三、计算题(本大题共1小题,共8.0分)
17. 因式分解:
.
四、解答题(本大题共7小题,共78.0分。解答应写出文字说明,证明过程或演算步骤)
18. 本小题分
解二元一次方程组:
;
.
19. 本小题分
先化简,再求值:,其中,.
20. 本小题分
已知:如图,点在直线上,点在直线上,,求证:.
21. 本小题分
某中学开展“英语演讲”比赛活动,七一、七二两个班根据初赛成绩,各选出名选手参加复赛,两个班各选出的名选手的复赛成绩满分为分如图所示.
根据图示填写下表;
班级 平均数分 中位数分 众数分
七一 ______ ______
七二 ______
计算两班复赛成绩的方差并说明哪班的成绩比较稳定;
如果在两班参加复赛的选手中分别选出人参加决赛,你认为哪个班的实力更强些?说明理由.
22. 本小题分
【例题讲解】因式分解:.
为三次二项式,若能因式分解,则可以分解成一个一次二项式和一个二次多项式的乘积故我们可以猜想可以分解成,展开等式右边得:,
恒成立.
等式两边多项式的同类项的对应系数相等,即,
解得,
.
【方法归纳】
设某一多项式的全部或部分系数为未知数,利用当两个多项式为恒等式时,同类项系数相等的原理确定这些系数,从而得到待求的值,这种方法叫待定系数法.
【学以致用】
若,则 ______ ;
若有一个因式是,求的值及另一个因式.
23. 本小题分
在疫情防控期间,某中学为保障广大师生生命健康安全,预从商场购进一批免洗手消毒液和消毒液如果购买瓶免洗手消毒液和瓶消毒液,共需花费元,如果购买瓶免洗手消毒液和瓶消毒液,共需花费元.
每瓶免洗手消毒液和每瓶消毒液的价格分别是多少元?
若商场有两种促销方案:方案一,所有购买商品均打八折;方案二,购买瓶免洗手消毒液送瓶消毒液,学校打算购进免洗手消毒液瓶,消毒液瓶,请问学校选用哪种方案更节约钱?节约多少钱?
24. 本小题分
如图,,点为直线上一定点,为直线上的动点,在直线与之间且在线段的右方作点,使得设为锐角.
求与的和;提示过点作
当点在直线上运动时,试说明;
当点在直线上运动的过程中,若平分,也恰好平分,请求出此时的值
答案和解析
1.【答案】
【解析】解:、不是轴对称图形,故本选项错误;
B、是轴对称图形,故本选项正确;
C、不是轴对称图形,故本选项错误;
D、不是轴对称图形,故本选项错误;
故选:.
根据轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,进行判断即可.
本题考查了轴对称图形的知识,属于基础题,掌握轴对称的定义是关键.
2.【答案】
【解析】解:,故选项A正确,
,故选项B错误,
,故选项C错误,
,故选项D错误,
故选:.
根据各个选项中的式子可以计算出正确的结果,从而可以解答本题.
本题考查整式的混合运算,解答本题的关键是明确整式的混合运算的计算方法.
3.【答案】
【解析】解:将代入原方程得:,
解得:,
的值为.
故选:.
将代入原方程,可得出关于的一元一次方程,解之即可求出的值.
本题考查了二元一次方程的解,牢记“一般地,使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解”是解题的关键.
4.【答案】
【解析】解:,
故选:.
根据是正整数可得,然后再根据是正整数可得,然后再代入计算即可.
此题主要考查了幂的乘方,以及同底数幂的乘法,关键是掌握幂的乘方法则:底数不变,指数相乘.同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加.
5.【答案】
【解析】【分析】
此题考查了解二元一次方程组,以及解一元一次方程,熟练掌握运算法则是解本题的关键.利用加减消元法判断即可.
【解答】
解方程组的最佳方法是加减法消去,得,
故选:.
6.【答案】
【解析】解:她的总得分是:.
故选:.
根据加权平均数的计算公式进行计算即可.
本题考查的是加权平均数,熟记加权平均数的计算公式是解决本题的关键.
7.【答案】
【解析】解:设的边上的高为.
,
,
,
.
故选:.
设的边上的高为构建方程求解.
本题考查三角形的面积,平行线的性质等知识,解题的关键是掌握等高模型,学会利用参数解决问题.
8.【答案】
【解析】解:相等的角不一定是对顶角,原命题是假命题;
在同一平面上,过一点有且只有一条直线与已知直线垂直,原命题是假命题;
平行于同一条直线的两条直线互相平行,是真命题;
同角或等角的余角相等,是真命题;
故选:.
根据对顶角、平行线的判定、等角的余角和垂直的判定进行判断即可.
此题考查平行线的判定和性质,关键是根据对顶角、平行线的判定、等角的余角和垂直的判定解答.
9.【答案】
【解析】解:,
,
得:,即,
将代入得:,即,
则原式.
故选C.
利用非负数的性质列出关于与的方程组,求出方程组的解得到与的值,即可求出所求式子的值.
此题考查了解二元一次方程组,以及非负数的性质,利用了消元的思想,消元的方法有:加减消元法与代入消元法.
10.【答案】
【解析】解:平分,平分,
,,
,
即,故正确;
设与交于,于交于,
,
,
,
,故正确;
平分,平分,
,,
,
,,
,
,,
,故正确;
,,
,
,
,
,
,
,
,
解得,
,故正确.
综上,正确答案有个,
故选:.
由角平分线的定义及平行线的性质可求解,即可判定;设与交于,于交于,由平行线的性质可得,结合三角形外角的性质可性质;由角平分线的定义可得,,结合平行线的性质可得,再利用三角形外角的性质可证明;由三角形外角的性质可得,根据直角三角形的性质及的结论可求解的度数,即可判定.
本题主要考查平行线的性质,角平分线的定义,三角形外角的性质,灵活运用性质解决问题是解题的关键.
11.【答案】
【解析】解:原式
.
故答案为:.
根据积的乘方计算即可.
本题考查幂的乘方与积的乘方,掌握运算法则是解题的关键.
12.【答案】
【解析】解:数据、、、、、、中,众数是,
,
这组数据按照从小到大排列是:、、、、、、,
这组数据的中位数是,
故答案为:.
根据数据、、、、、、中,众数是,可以得到的值,然后将数据按照从小到大排列,即可得到这组数据的中位数.
本题考查众数和中位数,解答本题的关键是明确题意,利用众数和中位数的知识解答.
13.【答案】
【解析】解:直线,与之间的距离为,与之间有一点,点到的距离是,
点到的距离是,
故答案为:.
根据直线,与之间的距离为,与之间有一点,点到的距离是,即可得出点到的距离.
本题主要考查了平行线之间的距离,从一条平行线上的任意一点到另一条直线作垂线,垂线段的长度叫两条平行线之间的距离.
14.【答案】
【解析】解:如图所示:
,
,
,
,
,且,
,
,
故答案为:.
利用两直线平行同位角相等得到一对角相等,再由对顶角相等及直角三角形两锐角互余求出所求角度数即可.
此题考查了平行线的性质、对顶角相等的性质、直角三角形的性质,熟练掌握平行线的性质是解本题的关键.
15.【答案】或
【解析】本题考查完全平方公式,解题的关键是熟练运用完全平方公式,本题属于基础题型.
根据完全平方公式即可求出答案.
解:,
,
或.
故答案为:或.
16.【答案】
【解析】解:,
,
故答案为:
利用完全平方公式计算即可求出值所求.
此题考查了完全平方公式,熟练掌握公式是解本题的关键.
17.【答案】解:;
.
【解析】原式提取公因式即可得到结果;
原式利用平方差公式,以及完全平方公式分解即可.
此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.
18.【答案】解:,
,得,
解得,
将代入,得,
解得,
原方程组的解为;
,
由得,,
由得,
,得,
解得,
将代入,得,
解得,
原方程组的解为.
【解析】根据加减消元法解二元一次方程组即可;
根据加减消元法解二元一次方程组即可.
本题考查了解二元一次方程组,熟练掌握解二元一次方程组的方法是解题的关键.
19.【答案】解:原式
,
把, 代入上式,原式.
【解析】先根据乘法公式算乘法,再合并同类项,最后求出答案即可.
本题考查了整式的混合运算和求值,能正确根据整式的运算法则进行化简是解此题的关键.
20.【答案】证明:,,
,
同位角相等,两直线平行,
,
,
,
同旁内角互补,两直线平行,
.
【解析】先根据题意得出,再由得出,故可得出,进而可得出结论.
本题考查的是平行线的判定与性质,熟知平行线的判定定理是解答此题的关键.
21.【答案】
【解析】解:由图可知七一班名选手的复赛成绩为:、、、、,七二班名选手的复赛成绩为:、、、、,
七一班的成绩的平均分是,
出现次数最多的是,则七一班的成绩的众数是;
七二班的成绩按从小到大的顺序排列,第位是,即七二班的中位数是.
填表:
班级 平均数分 中位数分 众数分
七一
七二
七一班的成绩比较稳定.理由如下:
,
,
,
七一班的成绩比较稳定;
七二班的实力更强些.理由如下:
七一班复赛成绩较好的前两名选手的成绩分别为,,
七二班复赛成绩较好的前两名选手的成绩分别为,,
在每班参加复赛的选手中分别选出人参加决赛,七二班的实力更强些.
观察图分别写出七一班和七二班名选手的复赛成绩,然后根据中位数的定义和平均数的求法以及众数的定义求解即可;
先根据方差公式分别计算两个班复赛成绩的方差,再根据方差的意义判断即可;
分别计算前两名的平均分,比较其大小.
本题考查了平均数、中位数、众数和方差的意义即运用.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定
22.【答案】
【解析】解:,
,
,
,
故答案为:;
设另一个因式为,
,
,
,,
解得,,
另一个因式为.
根据题目中的待定系数法原理即可求得结果;
根据待定系数法原理先设另一个多项式,然后根据恒等原理即可求得结论.
本题考查了因式分解的应用、多项式乘以多项式,解决本题的关键是理解并会运用待定系数法原理.
23.【答案】解:设每瓶免洗手消毒液价格是元,每瓶消毒液的价格是元,
由题意得:,
解得:,
每瓶免洗手消毒液价格是元,每瓶消毒液的价格是元,
答:每瓶免洗手消毒液价格是元,每瓶消毒液的价格是元;
方案一的花费为:元,
方案二的花费为:元,
,
方案一更节约钱,
节约钱为:元,
答:学校选用方案一更节约钱,节约元.
【解析】设每瓶免洗手消毒液价格是元,每瓶消毒液的价格是元,由“如果购买瓶免洗手消毒液和瓶消毒液,共需花费元,如果购买瓶免洗手消毒液和瓶消毒液,共需花费元”,列出二元一次方程组,解方程组即可;
分别求出方案一和方案二的花费情况,然后比较大小并作差即可.
本题考查了二元一次方程组的应用,找准等量关系,列出二元一次方程组是解题的关键.
24.【答案】解:如图,过点作,则.
,,
.
,
.
,
,
.
由得:,则.
,
,
.
若平分,也恰好平分,
则有,,.
,
,
.
由知:,
则,
解得:.
【解析】过点作,则,,依据平行线的性质可得到,则,最后,依据垂线的定义求解即可;
由得,然后结合,进行证明即可;
先求得的度数用含的式子表示,然后再利用中的结论列方程求解即可.
本题主要考查的是平行线的性质和判定,熟练掌握平行线的性质定理是解题的关键.
第1页,共1页
同课章节目录
