2023-2024学年人教版数学八年级上册 12.2.全等三角形判定(2)课件(共21张PPT)
文档属性
| 名称 | 2023-2024学年人教版数学八年级上册 12.2.全等三角形判定(2)课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-18 18:13:37 | ||
图片预览




文档简介
(共21张PPT)
塔城四中欢迎您!
12.2 三角形全等的判定(2)
八年级数学上册
学习目标:
1.理解“边角边”证明两个三角形全等的方法
2.会用“边角边”的条件证明两个三角形全等
自学指导:
请认真自学课本第37页探究3—38页练习以上的内容,并思考完成:
1.动手操作探究3,由此得出的结论有什么规律?
2.认真阅读例2并完成云朵中的问题。
5分钟后,能使用边角边判断两个三角形全等。
A
B
C
A′
D
E
现象:两个三角形放在一起
能完全重合.
说明:△ABC≌△A′B′C′
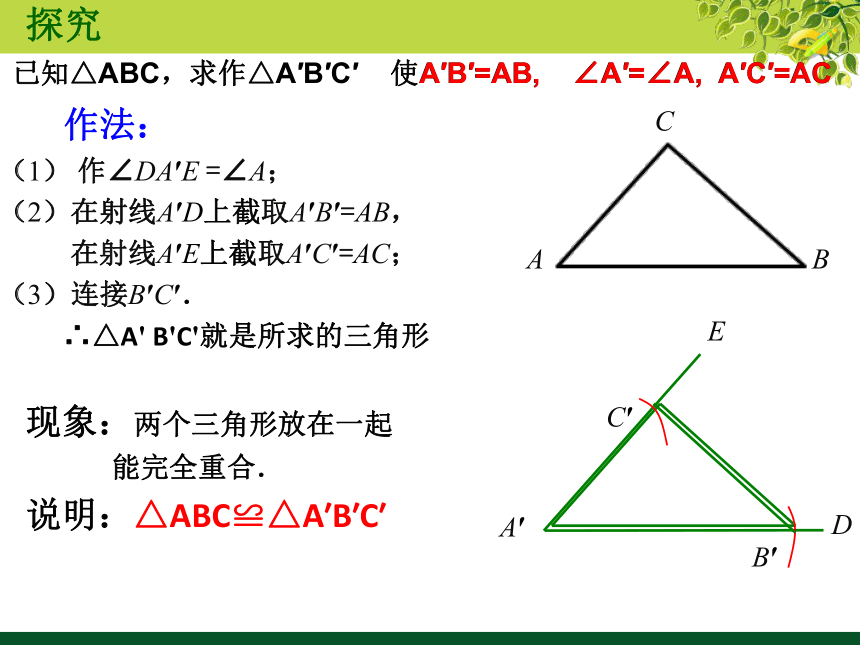
作法:
(1) 作∠DA′E =∠A;
(2)在射线A′D上截取A′B′=AB,
在射线A′E上截取A′C′=AC;
(3)连接B′C′.
∴△A' B'C'就是所求的三角形
B′
C′
已知△ABC,求作△A′B′C′ 使A′B′=AB, ∠A′=∠A, A′C′=AC
探究
A′B′=AB, ∠A′=∠A, A′C′=AC
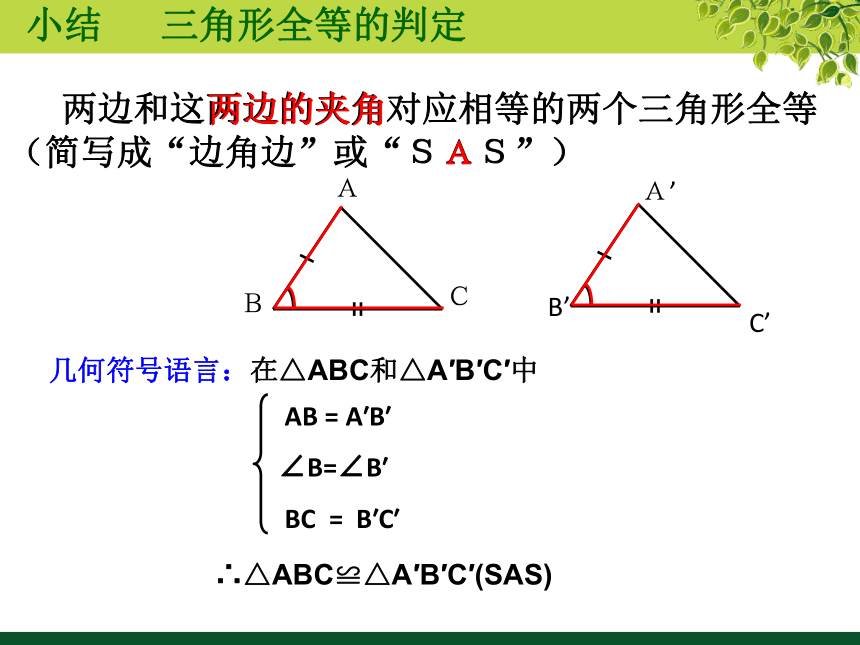
两边和这两边的夹角对应相等的两个三角形全等(简写成“边角边”或“SAS”)
两边的夹角
几何符号语言:在△ABC和△A′B′C′中
AB = A′B′
∠B=∠B′
BC = B′C′
∴△ABC≌△A′B′C′(SAS)
小结 三角形全等的判定
A
A
B
C
A’
C’
B’
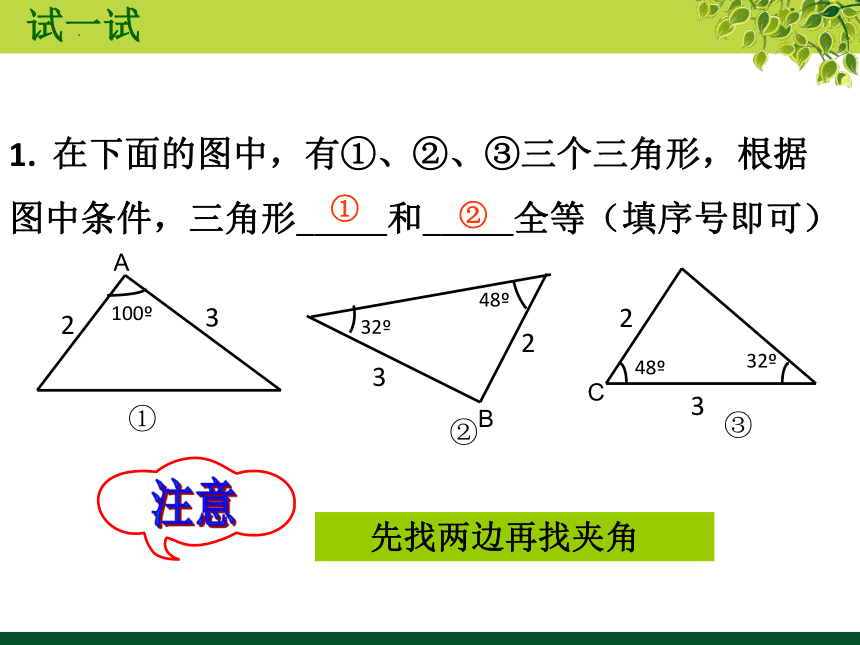
1. 在下面的图中,有①、②、③三个三角形,根据
图中条件,三角形_____和_____全等(填序号即可)
①
2
3
100
③
2
3
48
32
②
2
3
48
32
①
②
注意
先找两边再找夹角
试一试
A
B
C
OA=OC ,OB=OD
A
B
C
D
O
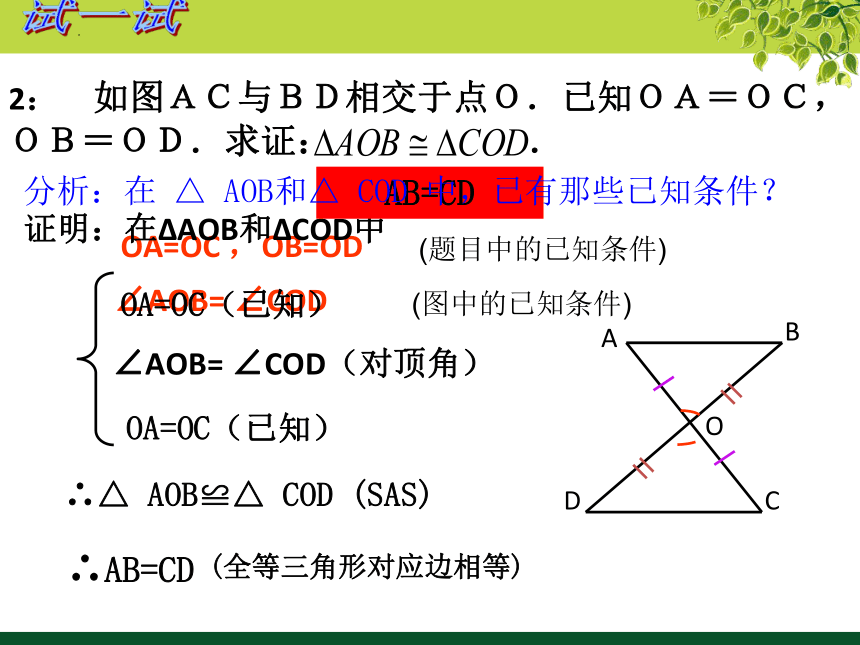
2: 如图AC与BD相交于点O.已知OA=OC,OB=OD.求证: .
∠AOB= ∠COD
试一试
证明:在 AOB和 COD中
OA=OC(已知)
OA=OC(已知)
∠AOB= ∠COD(对顶角)
∴△ AOB≌△ COD (SAS)
(题目中的已知条件)
(图中的已知条件)
AB=CD
∴AB=CD
分析:在 △ AOB和△ COD 中,已有那些已知条件?
(全等三角形对应边相等)
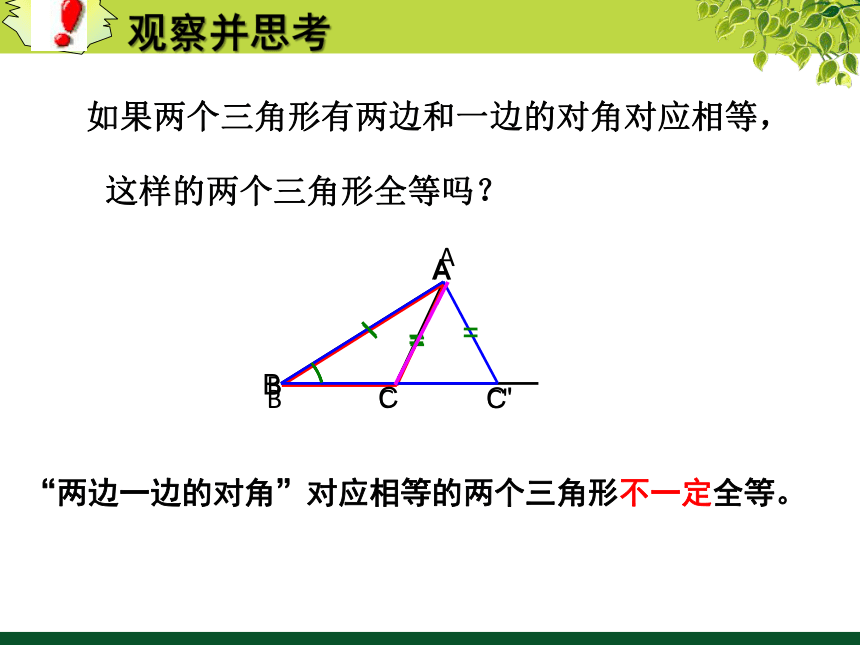
如果两个三角形有两边和一边的对角对应相等,
观察并思考
“两边一边的对角”对应相等的两个三角形不一定全等。
A
B
C
A
B
C'
A
B
C'
C
这样的两个三角形全等吗?
思考题:若AB=AC,则添加一个什么条件
可得△ABD≌ △ACD
A
B
D
C
1
2
AB=AC
AD=AD
SSS
SSA
×
AB=AC
AD=AD
SAS
AB=AC
AD=AD
∠1=∠2
BD=CD
∠B=∠C
依据
AB=AC
AD=AD
∠3=∠4
3
4
证明:∵∠BAC=∠DAE(已知)
∠ BAC+ ∠ CAD= ∠DAE+ ∠ CAD
∴∠BAD=∠CAE
在△ABD与△ACE中
AB=AC(已知)
∠BAD= ∠CAE (已证)
AD=AE(已知)
A
B
D
C
E
1已知:如图AB=AC,AD=AE,∠BAC=∠DAE
求证: △ABD≌△ACE
求证; BD=CE
能力提升:
∴△ABD≌△ACE(SAS)
3
1
2
1、今天我们学习哪种方法判定两三角形全等?
边角边(SAS)
2、通过这节课,判定三角形全等的方法有哪些?
SSS、SAS
注意哦!
“边边角”不能判定两个三角形全等
课堂小结
作业;
小册子14页第2课时
1 、已知B、C、E在同一条直线上, AC=DC
则添加一个什么条件,可得△ABD≌ △ACD
A
B
D
C
E
2、如图,点A,E,B,D在同一条直线上,AE=DB,AC=DF,AC∥DF.请探索BC与EF有怎样的位置关系?并说明理由.
F
E
B
A
C
D
测一测
2.如图,已知AB=AC,AD=AE
那么∠B与∠C 相等吗?为什么?
A
D
B
B
C
D
E
A
实践与拓展
理由:在△ ABD 和△ ACE中
AB=AC (已知)
AD=AD (公共边)
∠BAD=∠CAE (已知)
∴△ ABD ≌△ ACE (SAS)
∴∠B=∠C(全等三角形的对应角相等)
解: ∠B=∠C
A
B
C
D
∠A=∠A (公共角)
C
2.如图,已知AB=AC,∠BAD=∠CAD
那么∠B与∠C 相等吗?为什么?
AD=AE (已知)
如图,有一湖的湖岸在A、B之间呈一段圆弧状,
A、B间的距离不能直接测得.你能用已学过的知识
或方法设计测量方案,求出A、B间的距离吗
A
B
皮尺
学以致用
A
B
O
C
D
如图,有一湖的湖岸在A、B之间呈一段圆弧状,
A、B间的距离不能直接测得.你能用已学过的知识
或方法设计测量方案,求出A、B间的距离吗
学以致用
例2。如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA.连接BC并延长到E,CE=CB.连接DE,那么量出DE的长就是A、B的距离.为什么?
A
B
C
D
E
证明:
在△ABC和△DEC中,
CA=CD,
∠ACB=∠DCE,
CB=CE,
∴△ABC≌△DEC(SAS)
∴AB=DE.(全等三角形的对应角相等)
1.已知:如图, AB=CB ,∠ ABD= ∠ CBD ,
△ ABD 和△ CBD 全等吗?
解:
∴△ ABD ≌△ CBD (SAS)
AB=CB(已知)
∠ABD= ∠CBD(已知)
A
B
C
D
在△ ABD 和△ CBD中
BD=BD(公共边)
当堂检测
4 、已知AB=AC,AD=AE, ∠1= ∠2,
求证CE=BD。
C
B
A
D
E
2
1
证明:∵∠BAC=∠DAE(已知)
∠ BAC+ ∠ CAD= ∠DAE+ ∠ CAD
∴∠BAD=∠CAE
在△ABD与△ACE
AB=AC(已知)
∠BAD= ∠CAE (已证)
AD=AE(已知)
∴△ABD≌△ACE(SAS)
A
B
D
C
E
1已知:如图AB=AC,AD=AE,∠BAC=∠DAE
求证: △ABD≌△ACE
求证:1.BD=CE
2. ∠B= ∠C
3. ∠ADB= ∠AEC
能力提升:
塔城四中欢迎您!
12.2 三角形全等的判定(2)
八年级数学上册
学习目标:
1.理解“边角边”证明两个三角形全等的方法
2.会用“边角边”的条件证明两个三角形全等
自学指导:
请认真自学课本第37页探究3—38页练习以上的内容,并思考完成:
1.动手操作探究3,由此得出的结论有什么规律?
2.认真阅读例2并完成云朵中的问题。
5分钟后,能使用边角边判断两个三角形全等。
A
B
C
A′
D
E
现象:两个三角形放在一起
能完全重合.
说明:△ABC≌△A′B′C′
作法:
(1) 作∠DA′E =∠A;
(2)在射线A′D上截取A′B′=AB,
在射线A′E上截取A′C′=AC;
(3)连接B′C′.
∴△A' B'C'就是所求的三角形
B′
C′
已知△ABC,求作△A′B′C′ 使A′B′=AB, ∠A′=∠A, A′C′=AC
探究
A′B′=AB, ∠A′=∠A, A′C′=AC
两边和这两边的夹角对应相等的两个三角形全等(简写成“边角边”或“SAS”)
两边的夹角
几何符号语言:在△ABC和△A′B′C′中
AB = A′B′
∠B=∠B′
BC = B′C′
∴△ABC≌△A′B′C′(SAS)
小结 三角形全等的判定
A
A
B
C
A’
C’
B’
1. 在下面的图中,有①、②、③三个三角形,根据
图中条件,三角形_____和_____全等(填序号即可)
①
2
3
100
③
2
3
48
32
②
2
3
48
32
①
②
注意
先找两边再找夹角
试一试
A
B
C
OA=OC ,OB=OD
A
B
C
D
O
2: 如图AC与BD相交于点O.已知OA=OC,OB=OD.求证: .
∠AOB= ∠COD
试一试
证明:在 AOB和 COD中
OA=OC(已知)
OA=OC(已知)
∠AOB= ∠COD(对顶角)
∴△ AOB≌△ COD (SAS)
(题目中的已知条件)
(图中的已知条件)
AB=CD
∴AB=CD
分析:在 △ AOB和△ COD 中,已有那些已知条件?
(全等三角形对应边相等)
如果两个三角形有两边和一边的对角对应相等,
观察并思考
“两边一边的对角”对应相等的两个三角形不一定全等。
A
B
C
A
B
C'
A
B
C'
C
这样的两个三角形全等吗?
思考题:若AB=AC,则添加一个什么条件
可得△ABD≌ △ACD
A
B
D
C
1
2
AB=AC
AD=AD
SSS
SSA
×
AB=AC
AD=AD
SAS
AB=AC
AD=AD
∠1=∠2
BD=CD
∠B=∠C
依据
AB=AC
AD=AD
∠3=∠4
3
4
证明:∵∠BAC=∠DAE(已知)
∠ BAC+ ∠ CAD= ∠DAE+ ∠ CAD
∴∠BAD=∠CAE
在△ABD与△ACE中
AB=AC(已知)
∠BAD= ∠CAE (已证)
AD=AE(已知)
A
B
D
C
E
1已知:如图AB=AC,AD=AE,∠BAC=∠DAE
求证: △ABD≌△ACE
求证; BD=CE
能力提升:
∴△ABD≌△ACE(SAS)
3
1
2
1、今天我们学习哪种方法判定两三角形全等?
边角边(SAS)
2、通过这节课,判定三角形全等的方法有哪些?
SSS、SAS
注意哦!
“边边角”不能判定两个三角形全等
课堂小结
作业;
小册子14页第2课时
1 、已知B、C、E在同一条直线上, AC=DC
则添加一个什么条件,可得△ABD≌ △ACD
A
B
D
C
E
2、如图,点A,E,B,D在同一条直线上,AE=DB,AC=DF,AC∥DF.请探索BC与EF有怎样的位置关系?并说明理由.
F
E
B
A
C
D
测一测
2.如图,已知AB=AC,AD=AE
那么∠B与∠C 相等吗?为什么?
A
D
B
B
C
D
E
A
实践与拓展
理由:在△ ABD 和△ ACE中
AB=AC (已知)
AD=AD (公共边)
∠BAD=∠CAE (已知)
∴△ ABD ≌△ ACE (SAS)
∴∠B=∠C(全等三角形的对应角相等)
解: ∠B=∠C
A
B
C
D
∠A=∠A (公共角)
C
2.如图,已知AB=AC,∠BAD=∠CAD
那么∠B与∠C 相等吗?为什么?
AD=AE (已知)
如图,有一湖的湖岸在A、B之间呈一段圆弧状,
A、B间的距离不能直接测得.你能用已学过的知识
或方法设计测量方案,求出A、B间的距离吗
A
B
皮尺
学以致用
A
B
O
C
D
如图,有一湖的湖岸在A、B之间呈一段圆弧状,
A、B间的距离不能直接测得.你能用已学过的知识
或方法设计测量方案,求出A、B间的距离吗
学以致用
例2。如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA.连接BC并延长到E,CE=CB.连接DE,那么量出DE的长就是A、B的距离.为什么?
A
B
C
D
E
证明:
在△ABC和△DEC中,
CA=CD,
∠ACB=∠DCE,
CB=CE,
∴△ABC≌△DEC(SAS)
∴AB=DE.(全等三角形的对应角相等)
1.已知:如图, AB=CB ,∠ ABD= ∠ CBD ,
△ ABD 和△ CBD 全等吗?
解:
∴△ ABD ≌△ CBD (SAS)
AB=CB(已知)
∠ABD= ∠CBD(已知)
A
B
C
D
在△ ABD 和△ CBD中
BD=BD(公共边)
当堂检测
4 、已知AB=AC,AD=AE, ∠1= ∠2,
求证CE=BD。
C
B
A
D
E
2
1
证明:∵∠BAC=∠DAE(已知)
∠ BAC+ ∠ CAD= ∠DAE+ ∠ CAD
∴∠BAD=∠CAE
在△ABD与△ACE
AB=AC(已知)
∠BAD= ∠CAE (已证)
AD=AE(已知)
∴△ABD≌△ACE(SAS)
A
B
D
C
E
1已知:如图AB=AC,AD=AE,∠BAC=∠DAE
求证: △ABD≌△ACE
求证:1.BD=CE
2. ∠B= ∠C
3. ∠ADB= ∠AEC
能力提升:
