九年级数学上册(人教版) 23.2.1中心对称(课件)(共34张PPT)
文档属性
| 名称 | 九年级数学上册(人教版) 23.2.1中心对称(课件)(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 50.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-18 00:00:00 | ||
图片预览








文档简介
(共34张PPT)
第二十三章
旋转
23.2.1 中心对称
教学目标/Teaching aims
1
认识两个图形关于某一点中心对称的本质.
3
会画某图形关于某点对称的图形,会确定对称中心.
2
理解中心对称的性质,并可以判断两个图形是否成中心对称.
复习回顾
旋转中心
旋转方向
旋转度
①
②
③
旋转三要素
新课导入
1.时针从0时旋转到3时,旋转中心是 旋转角是多少度呢
2.从0时旋转到6时呢
o
旋转中心:点0 旋转角度:90°
旋转中心:点0 旋转角度:180°
中心对称的定义
新课导入
思考:
(1)如图,把其中一个图案绕点O 旋转180°,你有什么发现?
两个图案能够完全重合在一起.
新课导入
(2)如图,线段 AC,BD 相交于点 O,OA=OC,OB=OD.把 △OCD 绕点 O 旋转 180°,你有什么发现?
A
B
D
C
O
两个图案能够完全重合在一起.
中心对称的定义
归纳总结
像这样,把一个图形绕着某一点旋转180°,如果它能与另外一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心。
这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点。
中心对称的定义
新课导入
两个图形成中心对称需要满足什么条件?
中心对称的定义
①能找到一个对称中心;
②旋转角为180°;
③这两个图形旋转后能重合.
巩固练习
1.下列关于中心对称的描述不正确的是( )
A.把一个图形绕着某一点旋转,如果它能与另一个图形重合,那么就说这两个图形成中心对称
B.关于中心对称的两个图形是全等的
C.关于中心对称的两个图形,对称点的连线必过对称中心
D.如果两个图形关于点O对称,点A与A’是对称点,那么OA=OA’
A
2.如图,△ABC与△A′B′C′关于点O成中心对称.
(1)△ABC_________△A′B′C′,且点A的对称点是点_________,点B的对称点是点_________,点C的对称点是点_________;
(2)OA=_________,OB=_________,
OC=_________;
(3)点A、点O和点_________在同一直线
上;
(4)点O是线段_________,_________,_________的中点.
≌
A′
B′
C′
OA′
OB′
OC′
A′
AA′
BB′
CC′
巩固练习
探究新知
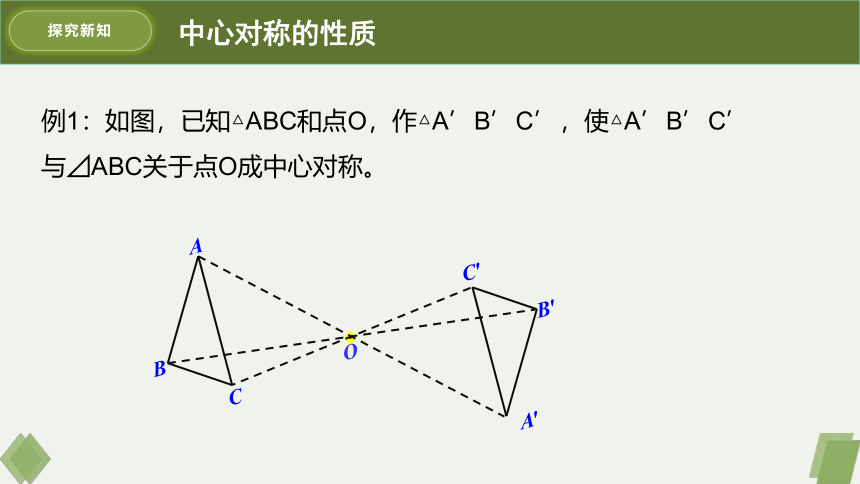
例1:如图,已知△ABC和点O,作△A’B’C’,使△A’B’C’与⊿ABC关于点O成中心对称。
A′
B′
C′
A
B
C
O
中心对称的性质
探究新知
A′
B′
C′
A
B
C
O
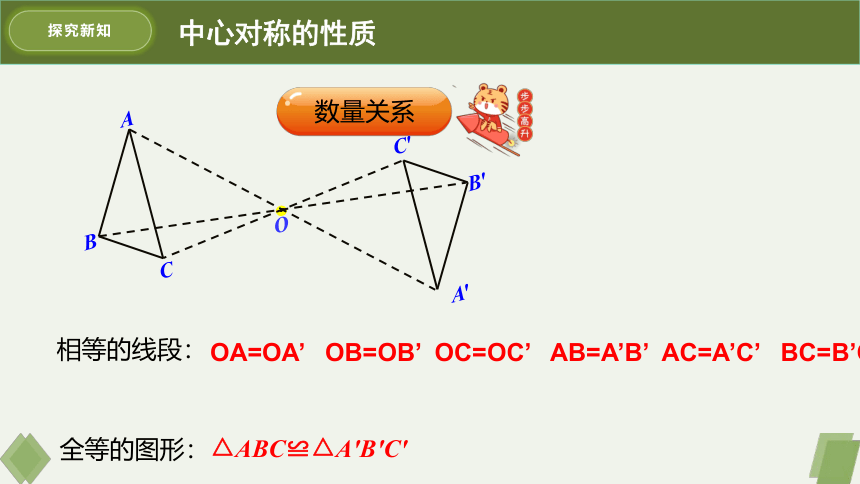
相等的线段:
全等的图形:
OA=OA’ OB=OB’ OC=OC’ AB=A’B’ AC=A’C’ BC=B’C’
△ABC≌△A′B′C′
数量关系
中心对称的性质
探究新知
位置关系
A′
B′
C′
A
B
C
O
对应线段:
AB∥A′B′ BC∥B′C′ AC∥A′C′
中心对称的性质
探究新知
例2:如图,旋转三角尺,画出△ABC关于点O中心对称的△A′B′C′ .
A′
C
A
B
B′
C′
O
●
中心对称的性质
探究新知
A′
C
A
B
B′
C′
O
●
数量关系
相等的线段:
全等的图形:
AB=A’B’ AC=A’C’ BC=B’C’
△ABC≌△A′B′C′
中心对称的性质
探究新知
A′
C
A
B
B′
C′
O
●
位置关系
对应线段:
全等的图形:
AC∥A’C’ BC∥B’C’
AB与A′B′在同一条直线上
中心对称的性质
归纳小结
中心对称的性质
中心对称的性质
①中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分。
②中心对称的两个图形是全等图形。
巩固练习
1.如图,△ABC与△A′B′C′关于点O成中心对称,则下列结论不成立的是( )
A.点A与点是对称点
B.BO=B’O
C.AB∥A’B’
D.∠ABC=∠C’A’B’
D
巩固练习
2.如图,点A,B分别是两个半圆的圆心,则该图案的对称中心是( )
A.点A B.点B C.线段AB的中点 D.无法确定
C
巩固练习
3.如图,△ABC和△DEF关于点O中心对称,若OB=4,则OE的长为______.
4
类比探究
思考:
中心对称与轴对称有什么不同?
轴对称 中心对称
定义三要点 1.有一条对称轴——直线 1.有一个对称中心——点
2.图形绕对称轴翻转180° 2.图形绕中心旋转180°
3.翻转后与另一个图形重合 3.旋转后与另一图形重合
性质 1.两个图形是全等形 1.两个图形是全等形
2.对称轴是对应点连线的垂直平分线 2.对称点是对应点连线的重点
3.对应线段或延长线相交,交点在对称轴上 3.对应点连线都经过对称中心
课堂练习
1.下列说法中错误的是( )
A.成中心对称的两个图形全等
B.中心对称图形绕对称中心旋转后,都能与自身重合
C.中心对称图形的对称中心是连结对称点的线段的中点
D.成中心对称的两个图形中,连结对称点的线段被对称轴平分
D
解析:中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分。
课堂练习
2.如图,在平面直角坐标系中,△ABC与△A1B1C1关于点E成中心对称.则对称中心点的坐标是( )
B
解析:中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分。因此找到对应点的连线的交点即为E点的坐标。
课堂练习
3.如图,数轴上点A与点B关于原点对称,则m=( ).
A.2 B.-2 C. D.
B
解析:中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分。因此点A到原点的距离等于点B到原点的距离,m为2的相反数。
课堂练习
4.如图,已知△AOB与△DOC成中心对称,△AOB的面积是12,AB=3,则△DOC中CD边上的高为________.
解析:设AB边上的高为h,因为△AOB的面积是12,AB=3,易得h=8.
又因为△AOB与△DOC成中心对称,△COD≌△AOB,所以△DOC中CD边上的高是8.
8
课堂练习
5.如图,如果△ABC和△DEF关于点G成中心对称,那么△ABC绕点G旋转_________°后能与△DEF重合.
180
解析:根据中心对称的定义
课堂练习
6.请按以下要求作图:
(1)如图1,线段AB和线段A′B′关于点M成中心对称,画出点M;
解:如答图1,点M即为所求.
图1
答图2
课堂练习
(2)如图3,△ABC和△A′B′C′关于点O成中心对称,画出△A′B′C′.
图3
答图4
解:如答图4,△A′B′C′即为所求.
课堂练习
6.如图13,将一张直角三角形纸片ABC沿中位线DE剪开后,在平面上将△BDE绕CB的中点D逆时针旋转180°,点E到了点E′的位置,点B和点C重合.求证:四边形ACE′E是平行四边形.
图13
课堂练习
课堂练习
解:(1)如图,点O为所作:
课堂练习
(2)∵△ABC和△DEF关于点O成中心对称,
∴△ABC≌△DEF,
∴DF=AC=6,DE=AB=5,EF=BC=4,
∴△DEF的周长=4+5+6=15;
(3)四边形ACDF为平行四边形.理由如下:
∵△ABC和△DEF关于点O成中心对称,
∴OA=OD,OC=OF,
∴四边形ACDF为平行四边形.
课堂总结
概念
旋转角是180°
性质
对应点的连线经过对称中心,且被对称中心平分
作图
应用1:作中心对称图形;
应用2:找出对称中心.
中心对称
能找到一个对称中心
两个图形旋转后重合
23.2.1 中心对称
谢谢观看
旋转
第二十三章
旋转
23.2.1 中心对称
教学目标/Teaching aims
1
认识两个图形关于某一点中心对称的本质.
3
会画某图形关于某点对称的图形,会确定对称中心.
2
理解中心对称的性质,并可以判断两个图形是否成中心对称.
复习回顾
旋转中心
旋转方向
旋转度
①
②
③
旋转三要素
新课导入
1.时针从0时旋转到3时,旋转中心是 旋转角是多少度呢
2.从0时旋转到6时呢
o
旋转中心:点0 旋转角度:90°
旋转中心:点0 旋转角度:180°
中心对称的定义
新课导入
思考:
(1)如图,把其中一个图案绕点O 旋转180°,你有什么发现?
两个图案能够完全重合在一起.
新课导入
(2)如图,线段 AC,BD 相交于点 O,OA=OC,OB=OD.把 △OCD 绕点 O 旋转 180°,你有什么发现?
A
B
D
C
O
两个图案能够完全重合在一起.
中心对称的定义
归纳总结
像这样,把一个图形绕着某一点旋转180°,如果它能与另外一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心。
这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点。
中心对称的定义
新课导入
两个图形成中心对称需要满足什么条件?
中心对称的定义
①能找到一个对称中心;
②旋转角为180°;
③这两个图形旋转后能重合.
巩固练习
1.下列关于中心对称的描述不正确的是( )
A.把一个图形绕着某一点旋转,如果它能与另一个图形重合,那么就说这两个图形成中心对称
B.关于中心对称的两个图形是全等的
C.关于中心对称的两个图形,对称点的连线必过对称中心
D.如果两个图形关于点O对称,点A与A’是对称点,那么OA=OA’
A
2.如图,△ABC与△A′B′C′关于点O成中心对称.
(1)△ABC_________△A′B′C′,且点A的对称点是点_________,点B的对称点是点_________,点C的对称点是点_________;
(2)OA=_________,OB=_________,
OC=_________;
(3)点A、点O和点_________在同一直线
上;
(4)点O是线段_________,_________,_________的中点.
≌
A′
B′
C′
OA′
OB′
OC′
A′
AA′
BB′
CC′
巩固练习
探究新知
例1:如图,已知△ABC和点O,作△A’B’C’,使△A’B’C’与⊿ABC关于点O成中心对称。
A′
B′
C′
A
B
C
O
中心对称的性质
探究新知
A′
B′
C′
A
B
C
O
相等的线段:
全等的图形:
OA=OA’ OB=OB’ OC=OC’ AB=A’B’ AC=A’C’ BC=B’C’
△ABC≌△A′B′C′
数量关系
中心对称的性质
探究新知
位置关系
A′
B′
C′
A
B
C
O
对应线段:
AB∥A′B′ BC∥B′C′ AC∥A′C′
中心对称的性质
探究新知
例2:如图,旋转三角尺,画出△ABC关于点O中心对称的△A′B′C′ .
A′
C
A
B
B′
C′
O
●
中心对称的性质
探究新知
A′
C
A
B
B′
C′
O
●
数量关系
相等的线段:
全等的图形:
AB=A’B’ AC=A’C’ BC=B’C’
△ABC≌△A′B′C′
中心对称的性质
探究新知
A′
C
A
B
B′
C′
O
●
位置关系
对应线段:
全等的图形:
AC∥A’C’ BC∥B’C’
AB与A′B′在同一条直线上
中心对称的性质
归纳小结
中心对称的性质
中心对称的性质
①中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分。
②中心对称的两个图形是全等图形。
巩固练习
1.如图,△ABC与△A′B′C′关于点O成中心对称,则下列结论不成立的是( )
A.点A与点是对称点
B.BO=B’O
C.AB∥A’B’
D.∠ABC=∠C’A’B’
D
巩固练习
2.如图,点A,B分别是两个半圆的圆心,则该图案的对称中心是( )
A.点A B.点B C.线段AB的中点 D.无法确定
C
巩固练习
3.如图,△ABC和△DEF关于点O中心对称,若OB=4,则OE的长为______.
4
类比探究
思考:
中心对称与轴对称有什么不同?
轴对称 中心对称
定义三要点 1.有一条对称轴——直线 1.有一个对称中心——点
2.图形绕对称轴翻转180° 2.图形绕中心旋转180°
3.翻转后与另一个图形重合 3.旋转后与另一图形重合
性质 1.两个图形是全等形 1.两个图形是全等形
2.对称轴是对应点连线的垂直平分线 2.对称点是对应点连线的重点
3.对应线段或延长线相交,交点在对称轴上 3.对应点连线都经过对称中心
课堂练习
1.下列说法中错误的是( )
A.成中心对称的两个图形全等
B.中心对称图形绕对称中心旋转后,都能与自身重合
C.中心对称图形的对称中心是连结对称点的线段的中点
D.成中心对称的两个图形中,连结对称点的线段被对称轴平分
D
解析:中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分。
课堂练习
2.如图,在平面直角坐标系中,△ABC与△A1B1C1关于点E成中心对称.则对称中心点的坐标是( )
B
解析:中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分。因此找到对应点的连线的交点即为E点的坐标。
课堂练习
3.如图,数轴上点A与点B关于原点对称,则m=( ).
A.2 B.-2 C. D.
B
解析:中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分。因此点A到原点的距离等于点B到原点的距离,m为2的相反数。
课堂练习
4.如图,已知△AOB与△DOC成中心对称,△AOB的面积是12,AB=3,则△DOC中CD边上的高为________.
解析:设AB边上的高为h,因为△AOB的面积是12,AB=3,易得h=8.
又因为△AOB与△DOC成中心对称,△COD≌△AOB,所以△DOC中CD边上的高是8.
8
课堂练习
5.如图,如果△ABC和△DEF关于点G成中心对称,那么△ABC绕点G旋转_________°后能与△DEF重合.
180
解析:根据中心对称的定义
课堂练习
6.请按以下要求作图:
(1)如图1,线段AB和线段A′B′关于点M成中心对称,画出点M;
解:如答图1,点M即为所求.
图1
答图2
课堂练习
(2)如图3,△ABC和△A′B′C′关于点O成中心对称,画出△A′B′C′.
图3
答图4
解:如答图4,△A′B′C′即为所求.
课堂练习
6.如图13,将一张直角三角形纸片ABC沿中位线DE剪开后,在平面上将△BDE绕CB的中点D逆时针旋转180°,点E到了点E′的位置,点B和点C重合.求证:四边形ACE′E是平行四边形.
图13
课堂练习
课堂练习
解:(1)如图,点O为所作:
课堂练习
(2)∵△ABC和△DEF关于点O成中心对称,
∴△ABC≌△DEF,
∴DF=AC=6,DE=AB=5,EF=BC=4,
∴△DEF的周长=4+5+6=15;
(3)四边形ACDF为平行四边形.理由如下:
∵△ABC和△DEF关于点O成中心对称,
∴OA=OD,OC=OF,
∴四边形ACDF为平行四边形.
课堂总结
概念
旋转角是180°
性质
对应点的连线经过对称中心,且被对称中心平分
作图
应用1:作中心对称图形;
应用2:找出对称中心.
中心对称
能找到一个对称中心
两个图形旋转后重合
23.2.1 中心对称
谢谢观看
旋转
同课章节目录
