2.1整式 探索规律问题 专项练习 (含答案)2023-2024学年人教版数学七年级上册
文档属性
| 名称 | 2.1整式 探索规律问题 专项练习 (含答案)2023-2024学年人教版数学七年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 148.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-18 00:00:00 | ||
图片预览

文档简介
2023年人教版数学七年级上册
《探索规律问题》专项练习
一 、选择题
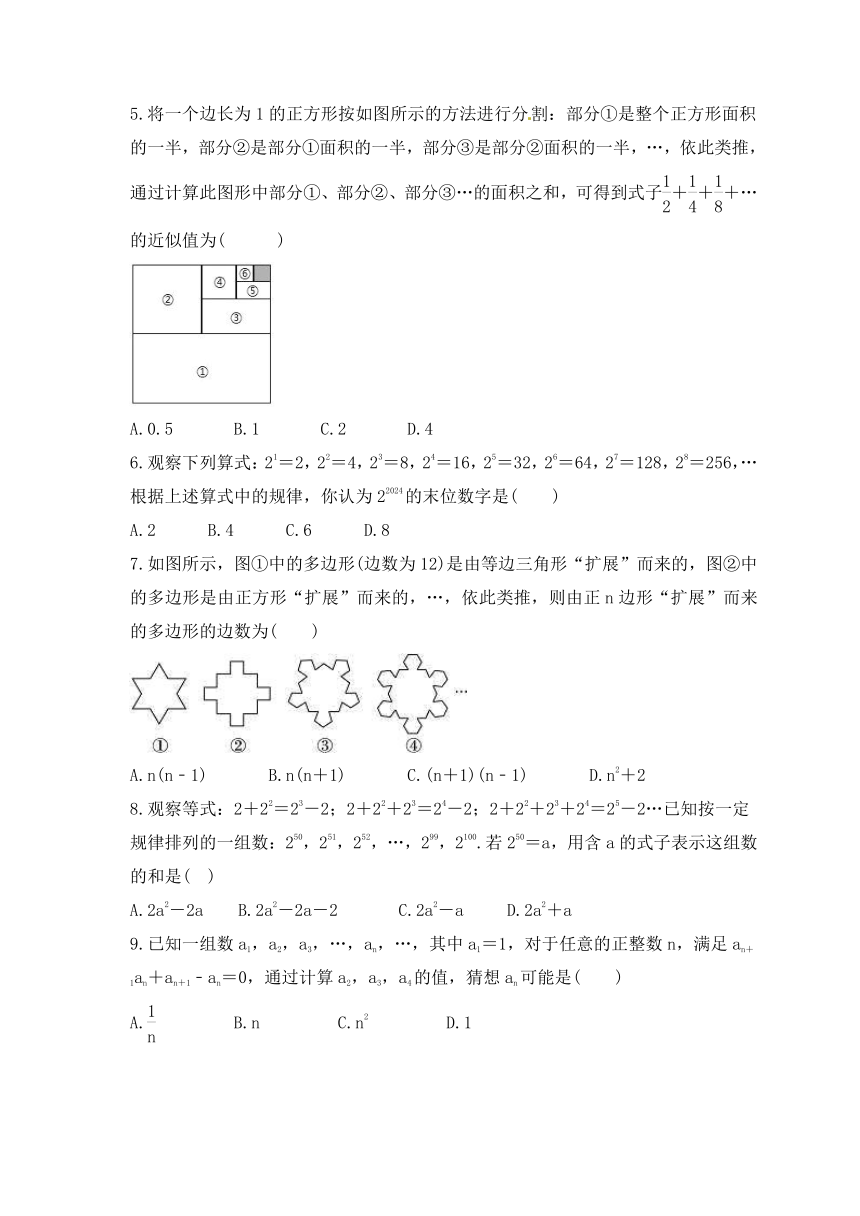
1.小王利用计算机设计了一个计算程序,输入和输出的数据如表:
输入 … 1 2 3 4 5 …
输出 … …
那么,当输入数据为8时,输出的数据为( )
A. B. C. D.
2.找出以如图形变化的规律,则第20个图形中黑色正方形的数量是( )
A.28 B.29 C.30 D.31
3.下列图形都是由同样大小的⊙按一定规律所组成的,其中第1个图形中一共有5个⊙,第2个图形中一共有8个⊙,第3个图形中一共有11个⊙,第4个图形中一共有14个⊙,…,按此规律排列,第1001个图形中基本图形的个数为( )
A.2998 B.3001 C.3002 D.3005
4.观察图并寻找规律,x处填上的数字是( )
A.﹣136 B.﹣150 C.﹣158 D.﹣162
5.将一个边长为1的正方形按如图所示的方法进行分割:部分①是整个正方形面积的一半,部分②是部分①面积的一半,部分③是部分②面积的一半,…,依此类推,通过计算此图形中部分①、部分②、部分③…的面积之和,可得到式子+++…的近似值为( )
A.0.5 B.1 C.2 D.4
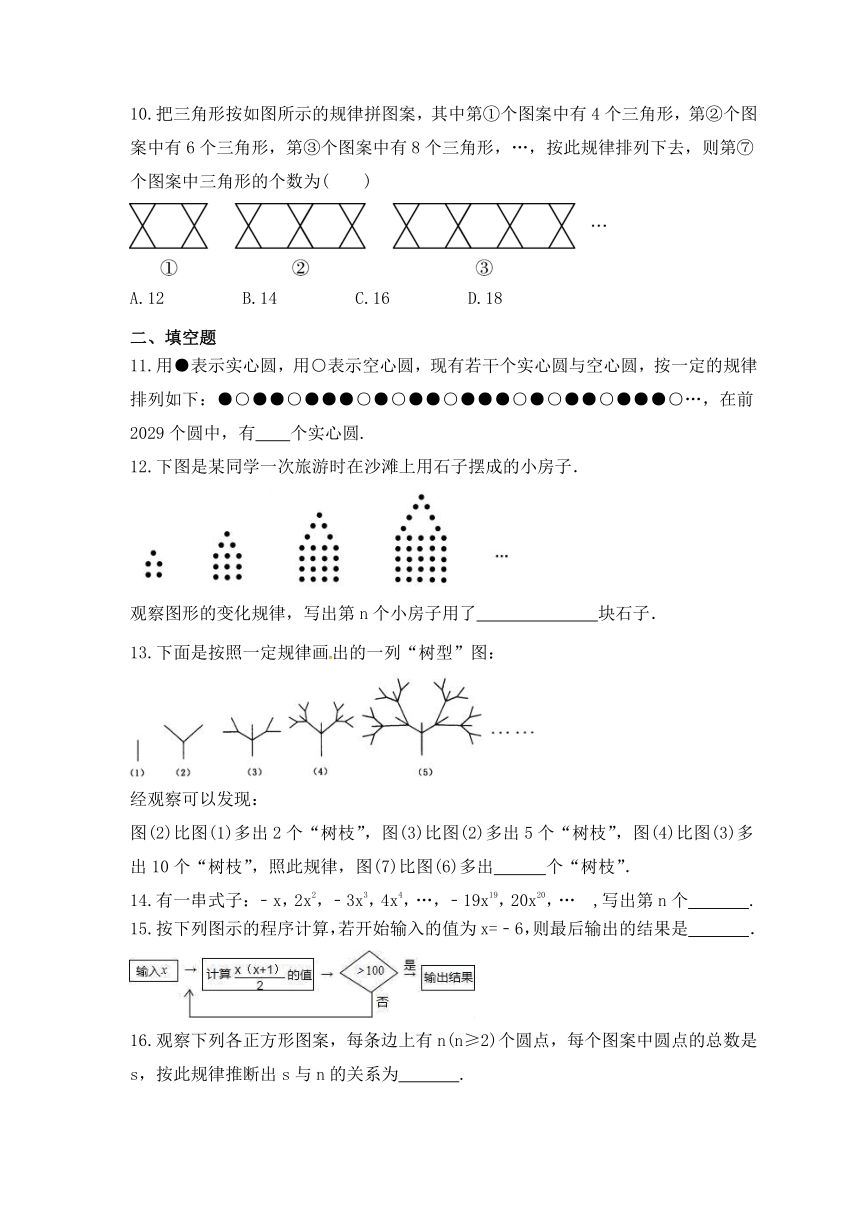
6.观察下列算式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…根据上述算式中的规律,你认为22024的末位数字是( )
A.2 B.4 C.6 D.8
7.如图所示,图①中的多边形(边数为12)是由等边三角形“扩展”而来的,图②中的多边形是由正方形“扩展”而来的,…,依此类推,则由正n边形“扩展”而来的多边形的边数为( )
A.n(n﹣1) B.n(n+1) C.(n+1)(n﹣1) D.n2+2
8.观察等式:2+22=23-2;2+22+23=24-2;2+22+23+24=25-2…已知按一定规律排列的一组数:250,251,252,…,299,2100.若250=a,用含a的式子表示这组数的和是( )
A.2a2-2a B.2a2-2a-2 C.2a2-a D.2a2+a
9.已知一组数a1,a2,a3,…,an,…,其中a1=1,对于任意的正整数n,满足an+1an+an+1﹣an=0,通过计算a2,a3,a4的值,猜想an可能是( )
A. B.n C.n2 D.1
10.把三角形按如图所示的规律拼图案,其中第①个图案中有4个三角形,第②个图案中有6个三角形,第③个图案中有8个三角形,…,按此规律排列下去,则第⑦个图案中三角形的个数为( )
A.12 B.14 C.16 D.18
二 、填空题
11.用●表示实心圆,用○表示空心圆,现有若干个实心圆与空心圆,按一定的规律排列如下:●○●●○●●●○●○●●○●●●○●○●●○●●●○…,在前2029个圆中,有 个实心圆.
12.下图是某同学一次旅游时在沙滩上用石子摆成的小房子.
观察图形的变化规律,写出第n个小房子用了 块石子.
13.下面是按照一定规律画出的一列“树型”图:
经观察可以发现:
图(2)比图(1)多出2个“树枝”,图(3)比图(2)多出5个“树枝”,图(4)比图(3)多出10个“树枝”,照此规律,图(7)比图(6)多出 个“树枝”.
14.有一串式子:﹣x,2x2,﹣3x3,4x4,…,﹣19x19,20x20,… ,写出第n个 .
15.按下列图示的程序计算,若开始输入的值为x=﹣6,则最后输出的结果是 .
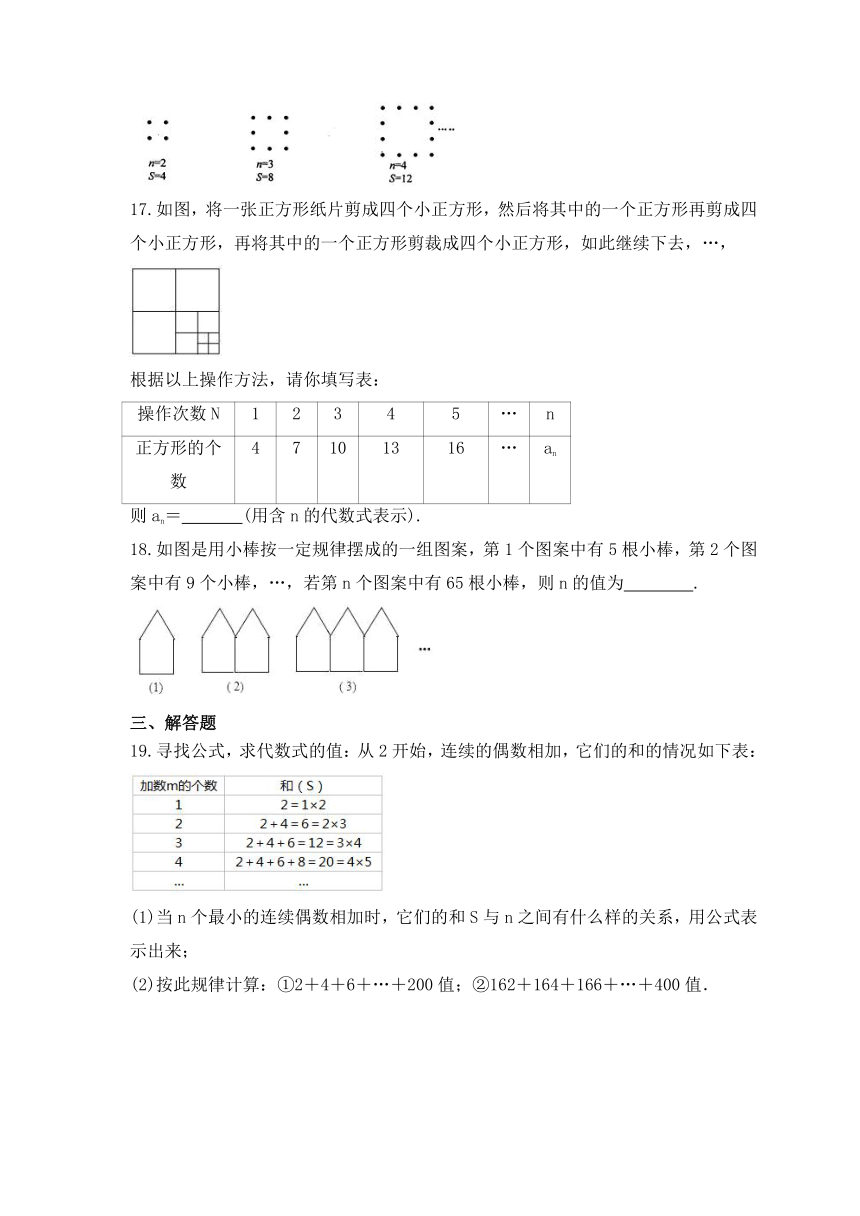
16.观察下列各正方形图案,每条边上有n(n≥2)个圆点,每个图案中圆点的总数是s,按此规律推断出s与n的关系为 .
17.如图,将一张正方形纸片剪成四个小正方形,然后将其中的一个正方形再剪成四个小正方形,再将其中的一个正方形剪裁成四个小正方形,如此继续下去,…,
根据以上操作方法,请你填写表:
操作次数N 1 2 3 4 5 … n
正方形的个数 4 7 10 13 16 … an
则an= (用含n的代数式表示).
18.如图是用小棒按一定规律摆成的一组图案,第1个图案中有5根小棒,第2个图案中有9个小棒,…,若第n个图案中有65根小棒,则n的值为 .
三 、解答题
19.寻找公式,求代数式的值:从2开始,连续的偶数相加,它们的和的情况如下表:
(1)当n个最小的连续偶数相加时,它们的和S与n之间有什么样的关系,用公式表示出来;
(2)按此规律计算:①2+4+6+…+200值;②162+164+166+…+400值.
20.下面的图形是由边长为l的正方形按照某种规律排列而组成的.
(1)观察图形,填写下表:
图形 ① ② ③
正方形的个数 8
图形的周长 18
(2)推测第n个图形中,正方形的个数为 ,周长为 (都用含n的代数式表示).
(3)这些图形中,任意一个图形的周长y与它所含正方形个数x之间的关系可表示为y= .
21.用火柴棒摆出下列一组图形:
(1)填写下表:
图形编号 1 2 3
图形中的火柴棒数
(2)照这样的方式摆下去,写出摆第n个图形中的火柴棒数;(用含n的代数式表示)
(3)如果某一图形共有2027根火柴棒,你知道它是第几个图形吗?
22.观察下列等式:
13=12
13+23=32
13+23+33=62
13+23+33+43=102…
(1)根据观察得到规律写出:13+23+33+43+53= .
(2)根据观察得到规律写出13+23+33+43+…+1003= .
(3)13+23+33+43+53+…+n3= .
23.阅读材料:求1+2+22+23+24+…+22023的值.
解:设S=1+2+22+23+24+…+22022+22023,将等式两边同时乘以2得:
2S=2+22+23+24+25+…+22023+22024
将下式减去上式得2S﹣S=22024﹣1
即S=22024﹣1
即1+2+22+23+24+…+22023=22024﹣1
请你仿照此法计算:
(1)1+2+22+23+24+…+210
(2)1+3+32+33+34+…+3n(其中n为正整数).
答案
1.C
2.C.
3.D.
4.D.
5.B.
6.C.
7.B.
8.C
9.A
10.C
11.答案为:1353.
12.答案为:(n2+4n).
13.答案为:80.
14.答案为:(﹣1)nnxn .
15.答案为:120.
16.答案为:S=4(n﹣1).
17.答案为:1+3n.
18.答案为:16.
19.解:(1))∵1个最小的连续偶数相加时,S=1×(1+1),
2个最小的连续偶数相加时,S=2×(2+1),
3个最小的连续偶数相加时,S=3×(3+1),
…
∴n个最小的连续偶数相加时,S=n(n+1);
(2)①根据(1)得:
2+4+6+…+200=100×(100+1)=10100;
②162+164+166+…+400,
=(2+4+6+…+400)﹣(2+4+6+…+160),
=200×201﹣80×81,
=40200﹣6480,
=33720.
20.解:(1)∵n=1时,正方形有8个,即8=5×1+3,周长是18,即18=10×1+8;
n=2时,正方形有13个,即13=5×2+3,周长是28,即28=10×2+8;
n=3时,正方形有18个,即18=5×3+3,周长是38,即38=10×3+8;
(2)由(1)可知,n=n时,正方形有5n+3个,周长是10n+8.
(3)∵y=10n+8,x=5n+3,
∴y=2x+2.
21.解:(1)第一个图形中火柴棒数=2+5=7,
第二个图形中火柴棒数=2+5+5=12,
第三个图形中火柴棒数=2+5+5+5=17;
故答案为:7;12;17;
(2)由(1)的规律可知第n个图形的火柴棒根数=2+5n;
(3)由题意可知2027=2+5n,解得n=407,
∴是第402个图形.
22.解:(1)依题意,得13+23+33+43+53=(1+2+3+4+5)2=152=225;
(2)依题意,得13+23+33+…+1003=(1+2+3+…+100)2=50502;
(3)一般规律为:13+23+33+…+n3=(1+2+3+…+n)2=[]2.
故答案为225;50502;[]2.
23.解:(1)设S=1+2+22+23+24+…+210,
将等式两边同时乘以2得:2S=2+22+23+24+…+210+211,
将下式减去上式得:2S﹣S=211﹣1,即S=211﹣1,
则1+2+22+23+24+…+210=211﹣1;
(2)设S=1+3+32+33+34+…+3n①,
两边同时乘以3得:3S=3+32+33+34+…+3n+3n+1②,
②﹣①得:3S﹣S=3n+1﹣1,即S=(3n+1﹣1),
则1+3+32+33+34+…+3n=(3n+1﹣1).
《探索规律问题》专项练习
一 、选择题
1.小王利用计算机设计了一个计算程序,输入和输出的数据如表:
输入 … 1 2 3 4 5 …
输出 … …
那么,当输入数据为8时,输出的数据为( )
A. B. C. D.
2.找出以如图形变化的规律,则第20个图形中黑色正方形的数量是( )
A.28 B.29 C.30 D.31
3.下列图形都是由同样大小的⊙按一定规律所组成的,其中第1个图形中一共有5个⊙,第2个图形中一共有8个⊙,第3个图形中一共有11个⊙,第4个图形中一共有14个⊙,…,按此规律排列,第1001个图形中基本图形的个数为( )
A.2998 B.3001 C.3002 D.3005
4.观察图并寻找规律,x处填上的数字是( )
A.﹣136 B.﹣150 C.﹣158 D.﹣162
5.将一个边长为1的正方形按如图所示的方法进行分割:部分①是整个正方形面积的一半,部分②是部分①面积的一半,部分③是部分②面积的一半,…,依此类推,通过计算此图形中部分①、部分②、部分③…的面积之和,可得到式子+++…的近似值为( )
A.0.5 B.1 C.2 D.4
6.观察下列算式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…根据上述算式中的规律,你认为22024的末位数字是( )
A.2 B.4 C.6 D.8
7.如图所示,图①中的多边形(边数为12)是由等边三角形“扩展”而来的,图②中的多边形是由正方形“扩展”而来的,…,依此类推,则由正n边形“扩展”而来的多边形的边数为( )
A.n(n﹣1) B.n(n+1) C.(n+1)(n﹣1) D.n2+2
8.观察等式:2+22=23-2;2+22+23=24-2;2+22+23+24=25-2…已知按一定规律排列的一组数:250,251,252,…,299,2100.若250=a,用含a的式子表示这组数的和是( )
A.2a2-2a B.2a2-2a-2 C.2a2-a D.2a2+a
9.已知一组数a1,a2,a3,…,an,…,其中a1=1,对于任意的正整数n,满足an+1an+an+1﹣an=0,通过计算a2,a3,a4的值,猜想an可能是( )
A. B.n C.n2 D.1
10.把三角形按如图所示的规律拼图案,其中第①个图案中有4个三角形,第②个图案中有6个三角形,第③个图案中有8个三角形,…,按此规律排列下去,则第⑦个图案中三角形的个数为( )
A.12 B.14 C.16 D.18
二 、填空题
11.用●表示实心圆,用○表示空心圆,现有若干个实心圆与空心圆,按一定的规律排列如下:●○●●○●●●○●○●●○●●●○●○●●○●●●○…,在前2029个圆中,有 个实心圆.
12.下图是某同学一次旅游时在沙滩上用石子摆成的小房子.
观察图形的变化规律,写出第n个小房子用了 块石子.
13.下面是按照一定规律画出的一列“树型”图:
经观察可以发现:
图(2)比图(1)多出2个“树枝”,图(3)比图(2)多出5个“树枝”,图(4)比图(3)多出10个“树枝”,照此规律,图(7)比图(6)多出 个“树枝”.
14.有一串式子:﹣x,2x2,﹣3x3,4x4,…,﹣19x19,20x20,… ,写出第n个 .
15.按下列图示的程序计算,若开始输入的值为x=﹣6,则最后输出的结果是 .
16.观察下列各正方形图案,每条边上有n(n≥2)个圆点,每个图案中圆点的总数是s,按此规律推断出s与n的关系为 .
17.如图,将一张正方形纸片剪成四个小正方形,然后将其中的一个正方形再剪成四个小正方形,再将其中的一个正方形剪裁成四个小正方形,如此继续下去,…,
根据以上操作方法,请你填写表:
操作次数N 1 2 3 4 5 … n
正方形的个数 4 7 10 13 16 … an
则an= (用含n的代数式表示).
18.如图是用小棒按一定规律摆成的一组图案,第1个图案中有5根小棒,第2个图案中有9个小棒,…,若第n个图案中有65根小棒,则n的值为 .
三 、解答题
19.寻找公式,求代数式的值:从2开始,连续的偶数相加,它们的和的情况如下表:
(1)当n个最小的连续偶数相加时,它们的和S与n之间有什么样的关系,用公式表示出来;
(2)按此规律计算:①2+4+6+…+200值;②162+164+166+…+400值.
20.下面的图形是由边长为l的正方形按照某种规律排列而组成的.
(1)观察图形,填写下表:
图形 ① ② ③
正方形的个数 8
图形的周长 18
(2)推测第n个图形中,正方形的个数为 ,周长为 (都用含n的代数式表示).
(3)这些图形中,任意一个图形的周长y与它所含正方形个数x之间的关系可表示为y= .
21.用火柴棒摆出下列一组图形:
(1)填写下表:
图形编号 1 2 3
图形中的火柴棒数
(2)照这样的方式摆下去,写出摆第n个图形中的火柴棒数;(用含n的代数式表示)
(3)如果某一图形共有2027根火柴棒,你知道它是第几个图形吗?
22.观察下列等式:
13=12
13+23=32
13+23+33=62
13+23+33+43=102…
(1)根据观察得到规律写出:13+23+33+43+53= .
(2)根据观察得到规律写出13+23+33+43+…+1003= .
(3)13+23+33+43+53+…+n3= .
23.阅读材料:求1+2+22+23+24+…+22023的值.
解:设S=1+2+22+23+24+…+22022+22023,将等式两边同时乘以2得:
2S=2+22+23+24+25+…+22023+22024
将下式减去上式得2S﹣S=22024﹣1
即S=22024﹣1
即1+2+22+23+24+…+22023=22024﹣1
请你仿照此法计算:
(1)1+2+22+23+24+…+210
(2)1+3+32+33+34+…+3n(其中n为正整数).
答案
1.C
2.C.
3.D.
4.D.
5.B.
6.C.
7.B.
8.C
9.A
10.C
11.答案为:1353.
12.答案为:(n2+4n).
13.答案为:80.
14.答案为:(﹣1)nnxn .
15.答案为:120.
16.答案为:S=4(n﹣1).
17.答案为:1+3n.
18.答案为:16.
19.解:(1))∵1个最小的连续偶数相加时,S=1×(1+1),
2个最小的连续偶数相加时,S=2×(2+1),
3个最小的连续偶数相加时,S=3×(3+1),
…
∴n个最小的连续偶数相加时,S=n(n+1);
(2)①根据(1)得:
2+4+6+…+200=100×(100+1)=10100;
②162+164+166+…+400,
=(2+4+6+…+400)﹣(2+4+6+…+160),
=200×201﹣80×81,
=40200﹣6480,
=33720.
20.解:(1)∵n=1时,正方形有8个,即8=5×1+3,周长是18,即18=10×1+8;
n=2时,正方形有13个,即13=5×2+3,周长是28,即28=10×2+8;
n=3时,正方形有18个,即18=5×3+3,周长是38,即38=10×3+8;
(2)由(1)可知,n=n时,正方形有5n+3个,周长是10n+8.
(3)∵y=10n+8,x=5n+3,
∴y=2x+2.
21.解:(1)第一个图形中火柴棒数=2+5=7,
第二个图形中火柴棒数=2+5+5=12,
第三个图形中火柴棒数=2+5+5+5=17;
故答案为:7;12;17;
(2)由(1)的规律可知第n个图形的火柴棒根数=2+5n;
(3)由题意可知2027=2+5n,解得n=407,
∴是第402个图形.
22.解:(1)依题意,得13+23+33+43+53=(1+2+3+4+5)2=152=225;
(2)依题意,得13+23+33+…+1003=(1+2+3+…+100)2=50502;
(3)一般规律为:13+23+33+…+n3=(1+2+3+…+n)2=[]2.
故答案为225;50502;[]2.
23.解:(1)设S=1+2+22+23+24+…+210,
将等式两边同时乘以2得:2S=2+22+23+24+…+210+211,
将下式减去上式得:2S﹣S=211﹣1,即S=211﹣1,
则1+2+22+23+24+…+210=211﹣1;
(2)设S=1+3+32+33+34+…+3n①,
两边同时乘以3得:3S=3+32+33+34+…+3n+3n+1②,
②﹣①得:3S﹣S=3n+1﹣1,即S=(3n+1﹣1),
则1+3+32+33+34+…+3n=(3n+1﹣1).
