1.2 集合间的基本关系 课件(共21张PPT)
文档属性
| 名称 | 1.2 集合间的基本关系 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-18 14:51:14 | ||
图片预览








文档简介
1.2 集合间的基本关系
第一章 集合与常用逻辑用语
问题引入
我们知道,两个实数之间有相等关系、大小关系,如5=5,5<7,5>3,等等.两个集合之间是否也有类似的关系呢?
?
问题1:观察下面几个例子,类比实数之间的相等关系、大小关系,你能发现下面两个集合之间的关系吗?
(1)????={1,2,3},????={1,2,3,4,5};
(2)C为立德中学高一(2)班全体女生组成的集合,D为这个班全体学生组成的集合;
(3)????={????|????是两条边相等的三角形},????={????|????是等腰三角形}.
?
????中的元素都在????中.
?
????中的元素都在????中.
?
????=????,元素一样.
?
1,2,3包含在1,2,3,4,5中
?
女生包含在这个班的学生中
两条边相等的三角形就是等腰三角形
新知探索
可以发现,在(1)中,集合????的任何一个元素都是集合????的元素.这时我们说集合????包含于集合????,或集合????包含集合????.(2)中的集合C与集合D也有这种关系.
?
在数学中,我们经常用平面上封闭曲线的内部代表集合,这种图形称为????????????????图.这样,上述集合????与集合????的包含关系,可以用右图表示.
?
一般地,对于两个集合????,????,如果集合????中任意一个元素都是集合????中的元素,就称集合????为集合????的子集,记作?????????(或?????????),读作“????包含于????”(或“????包含于????”).
?
新知探索
在(3)中,由于“两条边相等的三角形”是等腰三角形,因此,集合????,集合????都是由所有等腰三角形组成的集合.因此,集合????,????都是由所有等腰三角形组成的集合.即集合????中任何一个元素都是集合????中的元素,同时,集合????中任意一个元素也都是集合????中的元素,这样集合????的元素与集合????的元素是一样的.
?
一般的如果集合????中的任何一个元素都是集合????的元素,同时集合????的任意一个元素都是集合????的元素,那么集合????与集合????相等,记作????=????.
也就是说,若?????????,且?????????,则????=????.
?
思考1:请你举出几个具有包含关系、相等关系的集合实例.
新知探索
如果集合?????????,但存在元素????∈????,且?????????,就称集合????是集合????的真子集,记作?????????(或?????????).
?
例如,在(1)中,????={1,2,3},????={1,2,3,4,5}.
?????????,但4∈????,且4???,所以集合????是集合????的真子集,
即?????????(或?????????).
?
又如,在(2)中,C为立德中学高一(2)班全体女生组成的集合,D为这个班全体学生组成的集合.?????????,但男生∈????,且男生?????,所以集合????是集合????的真子集,
即?????????(或?????????).
?
新知探索
我们知道,方程????2+1=0没有实数根,所以方程????2+1=0的实数根组成的集合中没有元素.此时,我们说方程????2+1=0的实数根组成的集合为空集?.
?
一般地,我们把不含任何元素的集合叫做空集,记为?,并规定:空集是任何集合的子集.
?
思考2:你能举出几个空集的例子吗?
新知探索
思考3:包含关系{????}?????与属于关系????∈????有什么区别?试结合实例作出解释.
注:包含关系刻画的是集合与集合间的关系;而属于关系刻画的是元素与集合间的关系.
?
由上述集合之间的基本关系,可以得到下列结论:
(1)任何一个集合是它本身的子集,即?????????;
(2)对于集合????,????,????,如果?????????,且?????????,那么?????????.
?
例如,在(1)中,????={1,2,3},????={1,2,3,4,5}.
我们有4∈????,4?????;我们还有?????????(或?????????).
?
新知探索
辨析1:判断正误:
(1)任何集合都有子集和真子集. ( )
(2)集合{????|????2+1=0,????∈????}=?. ( )
?
答案:×,√.
辨析2:下列四个集合中,是空集的是( ). A.{????|????+3=3} B.{(????,????)|????2=?????2,????,????∈????}
C.{????|????2≤0} D.{????|????2?????+1=0,????∈????}
?
答案:D.
例析
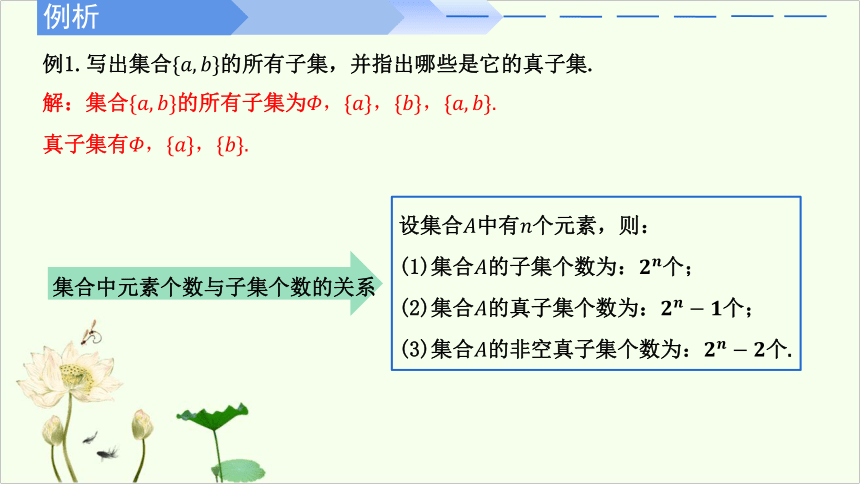
例1.写出集合{????,????}的所有子集,并指出哪些是它的真子集.
?
解:集合{????,????}的所有子集为????,{????},{????},{????,????}.
真子集有????,{????},{????}.
?
设集合????中有????个元素,则:
(1)集合????的子集个数为:????????个;
(2)集合????的真子集个数为:?????????????个;
(3)集合????的非空真子集个数为:?????????????个.
?
集合中元素个数与子集个数的关系
例析
例2.判断下列各题中集合????是否为集合????的子集,并说明理由:
(1)????={1,2,3},????={????|????是8的约数};
(2)????={????|????是长方形},????={????|????是两条对角线相等的平行四边形}.
?
解:(1)因为3不是8的约数,所以集合????不是集合????的子集.
(2)因为若????是长方形,则????一定是两条对角线相等的平行四边形,
所以集合????是集合????的子集.
?
练习
题型一:确定集合的子集、真子集
例1.已知集合????满足{1,2}??????{1,2,3,4,5},则所有满足条件????的集合的个数是( ).
A.6 B.7 C.8 D.9
?
答案:????.
解:由题意可以确定集合????必含有元素1,2,且至少含有元素3,4,5中的一个,因此依据集合????的元素个数分类如下:
含有3个元素:{1,2,3},{1,2,4},{1,2,5}.
含有4个元素:{1,2,3,4},{1,2,3,5},{1,2,4,5}.
含有5个元素:{1,2,3,4,5}.
故满足条件的集合????为{1,2,3},{1,2,4},{1,2,5},{1,2,3,4},{1,2,3,5},{1,2,4,5},{1,2,3,4,5}.
?
练习
变1.集合{????|????=?????2+6,????,????∈????}的真子集个数是( ).
A.9 B.8 C.7 D.6
?
答案:C.
解:当????=0时,????=6;当????=1时,????=5;
当????=2时,????=4;当????=3时,????=?3;
∵函数????=?????2+6,????∈????,在[0,+∞)上是减函数;
∴????≥3时,????<0;
∴{????∈????|????=?????2+6,????∈????}={2,5,6};
∴该集合的所有真子集为:?,{2},{5},{6},{2,5},{2,6},{5,6}.
∴该集合的真子集个数为7.
?
练习
方法技巧:
求集合子集、真子集个数的3个步骤
判断
分类
列举
根据子集、真子集的概念判断出集合中含有元素的可能情况
根据集合中元素的多少进行分类
采用列举法逐一写出每种情况的子集
练习
题型二:集合间关系的判断
例2.指出下列各组集合之间的关系:
(1)????={?1,1},????={(?1,?1),(?1,1),(1,?1),(1,1)};
(2)????={????|????是等边三角形},????={????|????是等腰三角形};
(3)????={????|????=2?????1,????∈?????},????={????|????=2????+1,????∈?????}.
?
答案:(1)????与????无包含关系;(2)?????????;(3)?????????.
解:(1)????中的元素为数,而????中的元素为点,因此????、????无包含关系.
(2)∵等边三角形一定是等腰三角形,∴?????????.
(3)∵????={1,3,5,7,9…},????={3,5,7,9,11…}
∴?????????.
?
练习
变2.已知集合????={????|????2?3????+2=0},????={1,2},????={????|????<8,????∈????},用适当的符号填空:
(1)A______B;(2)A______C;(3){2}______C;(4)2______C.
?
答案:(1)=;(2)?;(3)?;(4)∈.
解:∵集合????={????|????2?3????+2=0}={1,2},????={1,2},
????={????|????<8,????∈????}={0,1,2,3,4,5,6,7},
∴????=????,?????????,{2}?????,2∈????.
?
练习
方法技巧:
判断集合间关系的常用方法
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}列举观察法
当集合中元素较少时,可列出集合中的全部元素,通过定义得出集合之间的关系
集合元素特征法
首先确定集合的代表元素是什么,弄清集合元素的特征,再利用集合元素的特征判断关系
数形结
合法
利用数轴或?????????????????图,不等式的解集之间的关系,适用于数轴法
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}列举观察法
当集合中元素较少时,可列出集合中的全部元素,通过定义得出集合之间的关系
集合元素特征法
首先确定集合的代表元素是什么,弄清集合元素的特征,再利用集合元素的特征判断关系
数形结
合法
练习
题型三:由集合间的关系求参数
例3.已知集合????={?2≤????≤5},????={????|????+1≤????≤2?????1},若?????????,求实数????的取值范围.
?
解:∵????={?2≤????≤5},????={????|????+1≤????≤2?????1},若?????????,
∴分两种情况:
①当????=?时,则????+1>2?????1,即????<2;
②当????≠?时,则????+1≤2????+1????+1≥?22????+1≤5,即????≥2????≥?3????≤3.
解得:2≤????≤3.
综上可得,实数????的取值范围是:(?∞,3].
?
·
·
?2
?
5
?
????+1
?
2?????1
?
·
·
练习
解:据题意得:????≠?.
????+1≤?22?????1≥5,
解得,????≤?3????≥3, 即????无解.
?
变3.已知集合????={?2≤????≤5},????={????|????+1≤????≤2?????1},若?????????,求实数????的取值范围.
?
·
·
?2
?
5
?
????+1
?
2?????1
?
·
·
练习
方法技巧:
已知集合间的关系求参数问题的解题策略
(1)若已知集合是有限集,求解时,一般根据对应关系直接到方程.
(2)若已知集合是无限集,求解时,通常借助数轴,利用数轴分析法,将各个集合在数轴上表示出来,以形定数,还要注意验证端点值,做到准确无误.一般含“=”用实心圆点表示,不含“=”用空心圆圈表示.
(3)此类问题还要注意是否存在空集的情况,因为空集是任何集合的子集.
?
课堂小结&作业
课堂小结:
(1)集合间的基本关系;
(2)子集、真子集的关系及求解方法.
作业:
(1)整理本节课的题型;
(2)课本P8的练习1~3题;
(3)课本P9的习题1.2的1、2、3、4、5.
?
谢谢学习
Thank you for learning
第一章 集合与常用逻辑用语
问题引入
我们知道,两个实数之间有相等关系、大小关系,如5=5,5<7,5>3,等等.两个集合之间是否也有类似的关系呢?
?
问题1:观察下面几个例子,类比实数之间的相等关系、大小关系,你能发现下面两个集合之间的关系吗?
(1)????={1,2,3},????={1,2,3,4,5};
(2)C为立德中学高一(2)班全体女生组成的集合,D为这个班全体学生组成的集合;
(3)????={????|????是两条边相等的三角形},????={????|????是等腰三角形}.
?
????中的元素都在????中.
?
????中的元素都在????中.
?
????=????,元素一样.
?
1,2,3包含在1,2,3,4,5中
?
女生包含在这个班的学生中
两条边相等的三角形就是等腰三角形
新知探索
可以发现,在(1)中,集合????的任何一个元素都是集合????的元素.这时我们说集合????包含于集合????,或集合????包含集合????.(2)中的集合C与集合D也有这种关系.
?
在数学中,我们经常用平面上封闭曲线的内部代表集合,这种图形称为????????????????图.这样,上述集合????与集合????的包含关系,可以用右图表示.
?
一般地,对于两个集合????,????,如果集合????中任意一个元素都是集合????中的元素,就称集合????为集合????的子集,记作?????????(或?????????),读作“????包含于????”(或“????包含于????”).
?
新知探索
在(3)中,由于“两条边相等的三角形”是等腰三角形,因此,集合????,集合????都是由所有等腰三角形组成的集合.因此,集合????,????都是由所有等腰三角形组成的集合.即集合????中任何一个元素都是集合????中的元素,同时,集合????中任意一个元素也都是集合????中的元素,这样集合????的元素与集合????的元素是一样的.
?
一般的如果集合????中的任何一个元素都是集合????的元素,同时集合????的任意一个元素都是集合????的元素,那么集合????与集合????相等,记作????=????.
也就是说,若?????????,且?????????,则????=????.
?
思考1:请你举出几个具有包含关系、相等关系的集合实例.
新知探索
如果集合?????????,但存在元素????∈????,且?????????,就称集合????是集合????的真子集,记作?????????(或?????????).
?
例如,在(1)中,????={1,2,3},????={1,2,3,4,5}.
?????????,但4∈????,且4???,所以集合????是集合????的真子集,
即?????????(或?????????).
?
又如,在(2)中,C为立德中学高一(2)班全体女生组成的集合,D为这个班全体学生组成的集合.?????????,但男生∈????,且男生?????,所以集合????是集合????的真子集,
即?????????(或?????????).
?
新知探索
我们知道,方程????2+1=0没有实数根,所以方程????2+1=0的实数根组成的集合中没有元素.此时,我们说方程????2+1=0的实数根组成的集合为空集?.
?
一般地,我们把不含任何元素的集合叫做空集,记为?,并规定:空集是任何集合的子集.
?
思考2:你能举出几个空集的例子吗?
新知探索
思考3:包含关系{????}?????与属于关系????∈????有什么区别?试结合实例作出解释.
注:包含关系刻画的是集合与集合间的关系;而属于关系刻画的是元素与集合间的关系.
?
由上述集合之间的基本关系,可以得到下列结论:
(1)任何一个集合是它本身的子集,即?????????;
(2)对于集合????,????,????,如果?????????,且?????????,那么?????????.
?
例如,在(1)中,????={1,2,3},????={1,2,3,4,5}.
我们有4∈????,4?????;我们还有?????????(或?????????).
?
新知探索
辨析1:判断正误:
(1)任何集合都有子集和真子集. ( )
(2)集合{????|????2+1=0,????∈????}=?. ( )
?
答案:×,√.
辨析2:下列四个集合中,是空集的是( ). A.{????|????+3=3} B.{(????,????)|????2=?????2,????,????∈????}
C.{????|????2≤0} D.{????|????2?????+1=0,????∈????}
?
答案:D.
例析
例1.写出集合{????,????}的所有子集,并指出哪些是它的真子集.
?
解:集合{????,????}的所有子集为????,{????},{????},{????,????}.
真子集有????,{????},{????}.
?
设集合????中有????个元素,则:
(1)集合????的子集个数为:????????个;
(2)集合????的真子集个数为:?????????????个;
(3)集合????的非空真子集个数为:?????????????个.
?
集合中元素个数与子集个数的关系
例析
例2.判断下列各题中集合????是否为集合????的子集,并说明理由:
(1)????={1,2,3},????={????|????是8的约数};
(2)????={????|????是长方形},????={????|????是两条对角线相等的平行四边形}.
?
解:(1)因为3不是8的约数,所以集合????不是集合????的子集.
(2)因为若????是长方形,则????一定是两条对角线相等的平行四边形,
所以集合????是集合????的子集.
?
练习
题型一:确定集合的子集、真子集
例1.已知集合????满足{1,2}??????{1,2,3,4,5},则所有满足条件????的集合的个数是( ).
A.6 B.7 C.8 D.9
?
答案:????.
解:由题意可以确定集合????必含有元素1,2,且至少含有元素3,4,5中的一个,因此依据集合????的元素个数分类如下:
含有3个元素:{1,2,3},{1,2,4},{1,2,5}.
含有4个元素:{1,2,3,4},{1,2,3,5},{1,2,4,5}.
含有5个元素:{1,2,3,4,5}.
故满足条件的集合????为{1,2,3},{1,2,4},{1,2,5},{1,2,3,4},{1,2,3,5},{1,2,4,5},{1,2,3,4,5}.
?
练习
变1.集合{????|????=?????2+6,????,????∈????}的真子集个数是( ).
A.9 B.8 C.7 D.6
?
答案:C.
解:当????=0时,????=6;当????=1时,????=5;
当????=2时,????=4;当????=3时,????=?3;
∵函数????=?????2+6,????∈????,在[0,+∞)上是减函数;
∴????≥3时,????<0;
∴{????∈????|????=?????2+6,????∈????}={2,5,6};
∴该集合的所有真子集为:?,{2},{5},{6},{2,5},{2,6},{5,6}.
∴该集合的真子集个数为7.
?
练习
方法技巧:
求集合子集、真子集个数的3个步骤
判断
分类
列举
根据子集、真子集的概念判断出集合中含有元素的可能情况
根据集合中元素的多少进行分类
采用列举法逐一写出每种情况的子集
练习
题型二:集合间关系的判断
例2.指出下列各组集合之间的关系:
(1)????={?1,1},????={(?1,?1),(?1,1),(1,?1),(1,1)};
(2)????={????|????是等边三角形},????={????|????是等腰三角形};
(3)????={????|????=2?????1,????∈?????},????={????|????=2????+1,????∈?????}.
?
答案:(1)????与????无包含关系;(2)?????????;(3)?????????.
解:(1)????中的元素为数,而????中的元素为点,因此????、????无包含关系.
(2)∵等边三角形一定是等腰三角形,∴?????????.
(3)∵????={1,3,5,7,9…},????={3,5,7,9,11…}
∴?????????.
?
练习
变2.已知集合????={????|????2?3????+2=0},????={1,2},????={????|????<8,????∈????},用适当的符号填空:
(1)A______B;(2)A______C;(3){2}______C;(4)2______C.
?
答案:(1)=;(2)?;(3)?;(4)∈.
解:∵集合????={????|????2?3????+2=0}={1,2},????={1,2},
????={????|????<8,????∈????}={0,1,2,3,4,5,6,7},
∴????=????,?????????,{2}?????,2∈????.
?
练习
方法技巧:
判断集合间关系的常用方法
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}列举观察法
当集合中元素较少时,可列出集合中的全部元素,通过定义得出集合之间的关系
集合元素特征法
首先确定集合的代表元素是什么,弄清集合元素的特征,再利用集合元素的特征判断关系
数形结
合法
利用数轴或?????????????????图,不等式的解集之间的关系,适用于数轴法
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}列举观察法
当集合中元素较少时,可列出集合中的全部元素,通过定义得出集合之间的关系
集合元素特征法
首先确定集合的代表元素是什么,弄清集合元素的特征,再利用集合元素的特征判断关系
数形结
合法
练习
题型三:由集合间的关系求参数
例3.已知集合????={?2≤????≤5},????={????|????+1≤????≤2?????1},若?????????,求实数????的取值范围.
?
解:∵????={?2≤????≤5},????={????|????+1≤????≤2?????1},若?????????,
∴分两种情况:
①当????=?时,则????+1>2?????1,即????<2;
②当????≠?时,则????+1≤2????+1????+1≥?22????+1≤5,即????≥2????≥?3????≤3.
解得:2≤????≤3.
综上可得,实数????的取值范围是:(?∞,3].
?
·
·
?2
?
5
?
????+1
?
2?????1
?
·
·
练习
解:据题意得:????≠?.
????+1≤?22?????1≥5,
解得,????≤?3????≥3, 即????无解.
?
变3.已知集合????={?2≤????≤5},????={????|????+1≤????≤2?????1},若?????????,求实数????的取值范围.
?
·
·
?2
?
5
?
????+1
?
2?????1
?
·
·
练习
方法技巧:
已知集合间的关系求参数问题的解题策略
(1)若已知集合是有限集,求解时,一般根据对应关系直接到方程.
(2)若已知集合是无限集,求解时,通常借助数轴,利用数轴分析法,将各个集合在数轴上表示出来,以形定数,还要注意验证端点值,做到准确无误.一般含“=”用实心圆点表示,不含“=”用空心圆圈表示.
(3)此类问题还要注意是否存在空集的情况,因为空集是任何集合的子集.
?
课堂小结&作业
课堂小结:
(1)集合间的基本关系;
(2)子集、真子集的关系及求解方法.
作业:
(1)整理本节课的题型;
(2)课本P8的练习1~3题;
(3)课本P9的习题1.2的1、2、3、4、5.
?
谢谢学习
Thank you for learning
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
