生活中的旋转
图片预览


文档简介
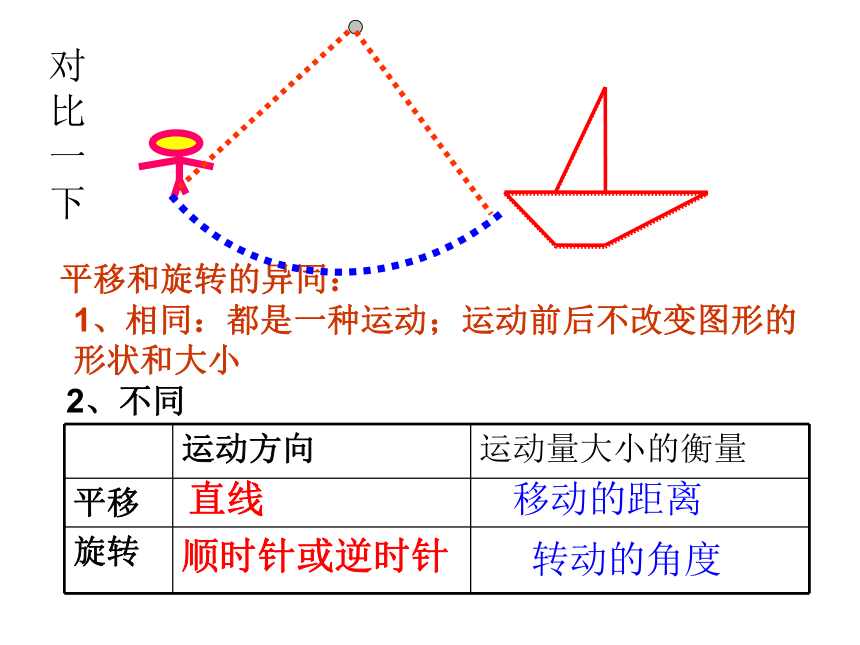
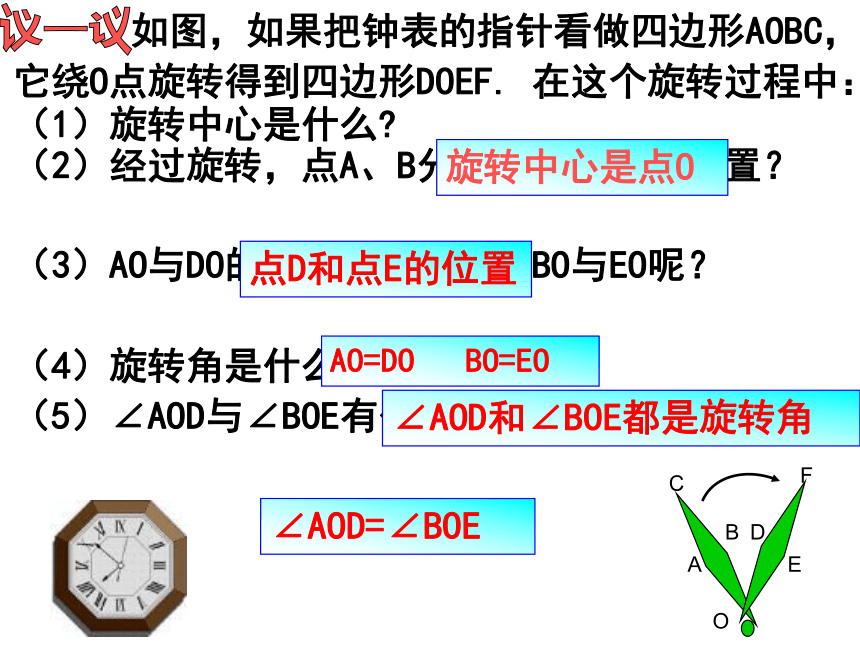
课件26张PPT。生活中的旋转平移和旋转的异同:2、不同直线顺时针或逆时针移动的距离转动的角度1、相同:都是一种运动;运动前后不改变图形的形状和大小对比一下 如图,如果把钟表的指针看做四边形AOBC,它绕O点旋转得到四边形DOEF. 在这个旋转过程中:
(1)旋转中心是什么?
(2)经过旋转,点A、B分别移动到什么位置?
(3)AO与DO的长有什么关系?BO与EO呢?
(4)旋转角是什么?
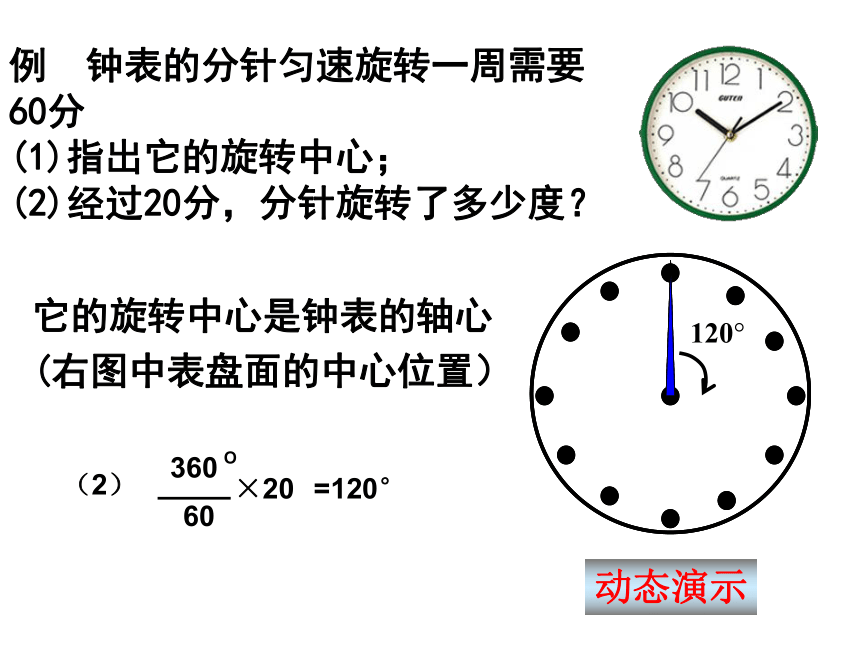
(5)∠AOD与∠BOE有什么大小关系?旋转中心是点O点D和点E的位置AO=DO BO=EO∠AOD=∠BOE∠AOD和∠BOE都是旋转角议一议●旋转前后,两图形的大小不变、形状不变;● 旋转前后,两图形任意一对对应点与旋转中心的连线所成的角都是旋转角,旋转角相等;对应点到旋转中心的距离相等.旋转的性质: 例 钟表的分针匀速旋转一周需要60分
(1)指出它的旋转中心;
(2)经过20分,分针旋转了多少度?它的旋转中心是钟表的轴心
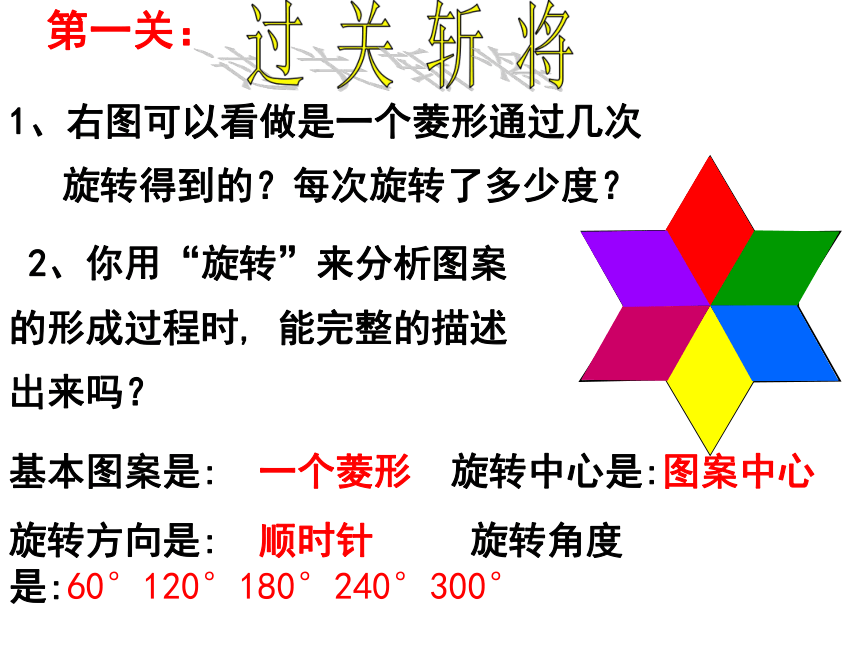
(右图中表盘面的中心位置)动态演示 2、你用“旋转”来分析图案的形成过程时, 能完整的描述出来吗?1、右图可以看做是一个菱形通过几次
旋转得到的?每次旋转了多少度?第一关:过 关 斩 将基本图案是: 一个菱形 旋转中心是:图案中心
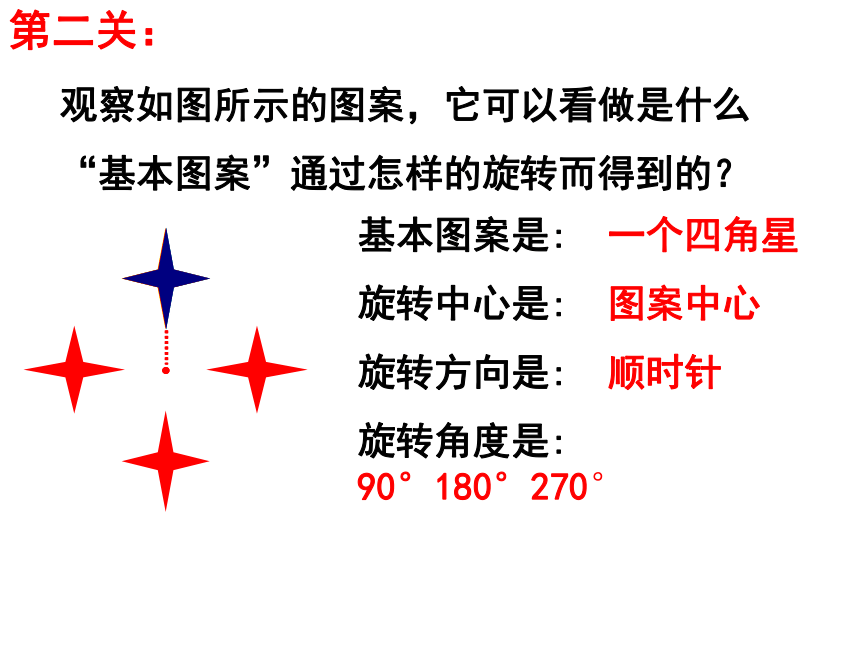
旋转方向是: 顺时针 旋转角度是:60°120°180°240°300°第二关:观察如图所示的图案,它可以看做是什么“基本图案”通过怎样的旋转而得到的?基本图案是: 一个四角星
旋转中心是: 图案中心
旋转方向是: 顺时针
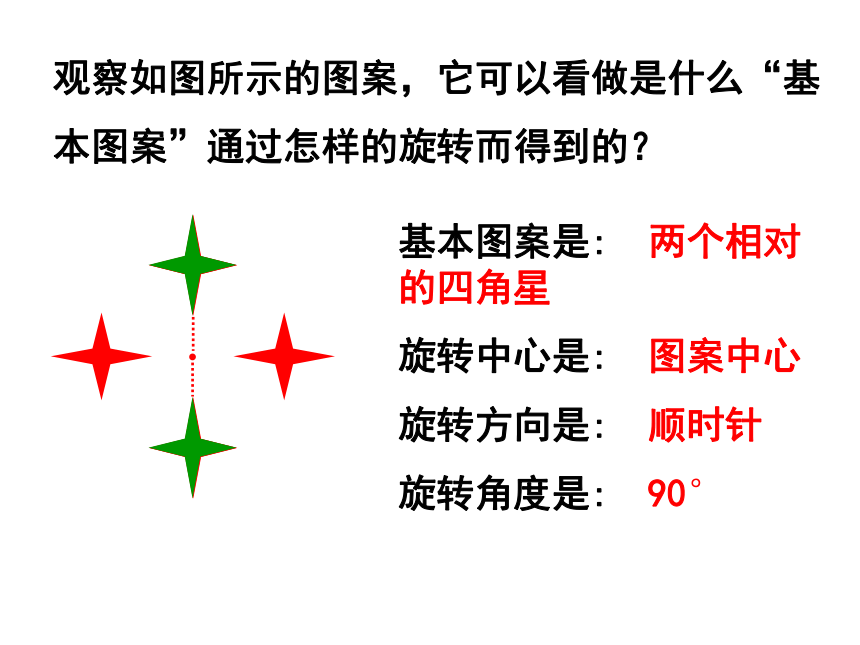
旋转角度是: 90°180°270°观察如图所示的图案,它可以看做是什么“基本图案”通过怎样的旋转而得到的?基本图案是: 两个相对的四角星
旋转中心是: 图案中心
旋转方向是: 顺时针
旋转角度是: 90°观察如图所示的图案,它可以看做是什么“基本图案”通过怎样的旋转而得到的?基本图案是: 两个相邻的四角星
旋转中心是: 图案中心
旋转方向是: 顺时针
旋转角度是: 180°第三关:如图:香港特别行政区区徽是由五个同样的花瓣组成的,它可以看做是什么“基本图案”通过怎样的旋转而得到的?基本图案是: 一个花瓣
旋转中心是: 图案中心
旋转方向是: 顺时针
旋转角度是: 72°144°216°288°第四关:如图:正方形ABCD与正方形EFGH边长相等,这个图案可以看做是哪个“基本图案”通过怎样的旋转得到的?如图:正方形ABCD与正方形EFGH边长相等,这个图案可以看做是哪个“基本图案”通过怎样的旋转得到的?如图:正方形ABCD与正方形EFGH边长相等,这个图案可以看做是哪个“基本图案”通过怎样的旋转得到的?第五关:如图,O是六个正三角形的公共顶点,正六边形ABCDEF能否看做是某条线段绕O点旋转若干次所形成的图形? 简单的旋转作图AO点的旋转作法例1 将A点绕O点沿顺时针方向旋转60?.作法:
1. 以点O为圆心,OA长为半径画圆;
2. 连接OA, 用量角器或三角板(限特殊角)作出∠AOB=60°,与圆周交于B点;
3. B点即为所求作.B 简单的旋转作图AO线段的旋转作法例2 将线段AB绕O点沿顺时针方向旋转60?.作法:
将点A绕点O顺时针旋转60?,得点C;
2. 将点B绕点O顺时针旋转60 ?,得点D ;
3. 连接CD, 则线段CD即为所求作.CBD简单的旋转作图图形的旋转作法例3 如图,△ABC绕C点旋转后,顶点A得对应点为点D. 试确定顶点B对应点的位置以及旋转后的三角形.作法一:
1. 连接CD;
2. 以CB为一边,作∠BCE,使得∠BCE=∠ACD ;
3. 在射线CB上截取CE,使得CE=CB;
4. 连接DE,则△DEC即为所求作.CABDE 已知线段AB和点O,请画出线段AB绕点O按逆时针旋转1000后的图形.例题ABO ⑴如图,画出△ABC绕点A按逆时针方向旋转900后的对应三角形;例题⑵如果点D是AC的中点,那么经过上述旋转后,点D旋转到什么位置?请在图中将点D的对应点
D′表示出来.(3).如果AD=1cm,那么点D旋转过的路径是多少?ABCDEF 2、如图,ΔDEF是由△ABC绕某一中心旋转一定的角度得到,请你找出这旋转中心.找旋转中心旋转中心在对应点连线的垂直平分线上。2.在等腰直角△ABC中,∠C=900,BC=2cm,如果以AC的中点O为旋转中心,将这个三角形旋转1800,点B落在点B′处,求BB′的长度.A/B/C/3.已知:如图,在△ABC中,∠BAC=1200,以BC为边向形外作等边三角形△BCD,把△ABD绕着点D按顺时针方向旋转600后得到△ECD,若AB=3,AC=2,求∠BAD的度数与AD的长. 简单的旋转作图练习1
将下图中大写字母N绕它右下侧的顶点按顺时针方向旋转90?,作出旋转后的图案.回顾与小结旋转的定义:在平面内,将一个图形绕一个定点沿着某个方向转动一定的角度,这样的图形运动称为旋转. 这个定点称为旋转中心,转动的角称为旋转角.
旋转的性质:
旋转不改变图形的大小与形状;
旋转前后两图形任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.
旋转的判定方法:利用旋转的性质判定旋转的存在.
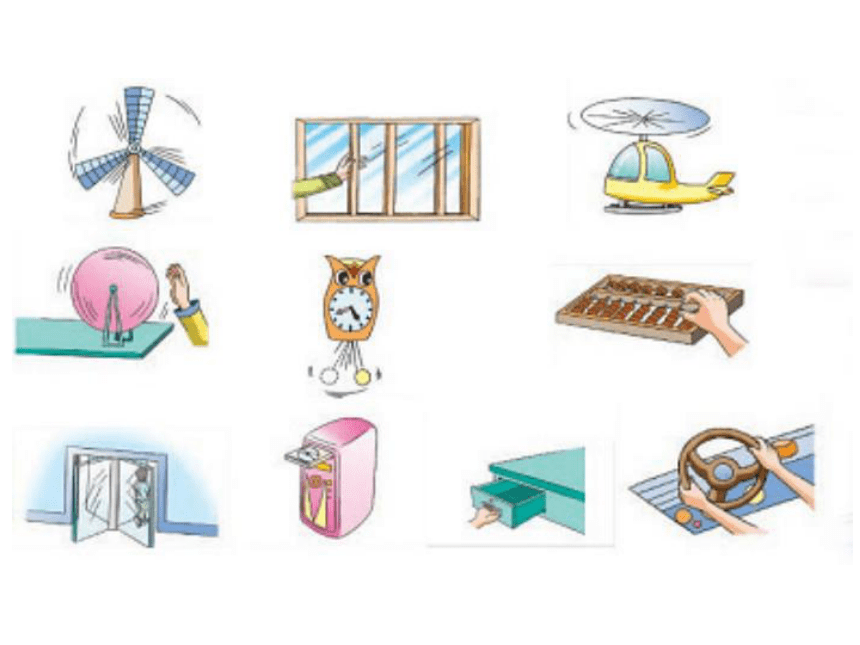
旋转的普遍性:旋转广泛存在于我们的生活中.
简单性与复杂性:简单图形旋转的复合可以产生复杂且美妙的图案,可见复杂性蕴藏于简单性之中. 研究旋转的规律可以帮助我们化繁为简,化难为易.谢谢大家
(1)旋转中心是什么?
(2)经过旋转,点A、B分别移动到什么位置?
(3)AO与DO的长有什么关系?BO与EO呢?
(4)旋转角是什么?
(5)∠AOD与∠BOE有什么大小关系?旋转中心是点O点D和点E的位置AO=DO BO=EO∠AOD=∠BOE∠AOD和∠BOE都是旋转角议一议●旋转前后,两图形的大小不变、形状不变;● 旋转前后,两图形任意一对对应点与旋转中心的连线所成的角都是旋转角,旋转角相等;对应点到旋转中心的距离相等.旋转的性质: 例 钟表的分针匀速旋转一周需要60分
(1)指出它的旋转中心;
(2)经过20分,分针旋转了多少度?它的旋转中心是钟表的轴心
(右图中表盘面的中心位置)动态演示 2、你用“旋转”来分析图案的形成过程时, 能完整的描述出来吗?1、右图可以看做是一个菱形通过几次
旋转得到的?每次旋转了多少度?第一关:过 关 斩 将基本图案是: 一个菱形 旋转中心是:图案中心
旋转方向是: 顺时针 旋转角度是:60°120°180°240°300°第二关:观察如图所示的图案,它可以看做是什么“基本图案”通过怎样的旋转而得到的?基本图案是: 一个四角星
旋转中心是: 图案中心
旋转方向是: 顺时针
旋转角度是: 90°180°270°观察如图所示的图案,它可以看做是什么“基本图案”通过怎样的旋转而得到的?基本图案是: 两个相对的四角星
旋转中心是: 图案中心
旋转方向是: 顺时针
旋转角度是: 90°观察如图所示的图案,它可以看做是什么“基本图案”通过怎样的旋转而得到的?基本图案是: 两个相邻的四角星
旋转中心是: 图案中心
旋转方向是: 顺时针
旋转角度是: 180°第三关:如图:香港特别行政区区徽是由五个同样的花瓣组成的,它可以看做是什么“基本图案”通过怎样的旋转而得到的?基本图案是: 一个花瓣
旋转中心是: 图案中心
旋转方向是: 顺时针
旋转角度是: 72°144°216°288°第四关:如图:正方形ABCD与正方形EFGH边长相等,这个图案可以看做是哪个“基本图案”通过怎样的旋转得到的?如图:正方形ABCD与正方形EFGH边长相等,这个图案可以看做是哪个“基本图案”通过怎样的旋转得到的?如图:正方形ABCD与正方形EFGH边长相等,这个图案可以看做是哪个“基本图案”通过怎样的旋转得到的?第五关:如图,O是六个正三角形的公共顶点,正六边形ABCDEF能否看做是某条线段绕O点旋转若干次所形成的图形? 简单的旋转作图AO点的旋转作法例1 将A点绕O点沿顺时针方向旋转60?.作法:
1. 以点O为圆心,OA长为半径画圆;
2. 连接OA, 用量角器或三角板(限特殊角)作出∠AOB=60°,与圆周交于B点;
3. B点即为所求作.B 简单的旋转作图AO线段的旋转作法例2 将线段AB绕O点沿顺时针方向旋转60?.作法:
将点A绕点O顺时针旋转60?,得点C;
2. 将点B绕点O顺时针旋转60 ?,得点D ;
3. 连接CD, 则线段CD即为所求作.CBD简单的旋转作图图形的旋转作法例3 如图,△ABC绕C点旋转后,顶点A得对应点为点D. 试确定顶点B对应点的位置以及旋转后的三角形.作法一:
1. 连接CD;
2. 以CB为一边,作∠BCE,使得∠BCE=∠ACD ;
3. 在射线CB上截取CE,使得CE=CB;
4. 连接DE,则△DEC即为所求作.CABDE 已知线段AB和点O,请画出线段AB绕点O按逆时针旋转1000后的图形.例题ABO ⑴如图,画出△ABC绕点A按逆时针方向旋转900后的对应三角形;例题⑵如果点D是AC的中点,那么经过上述旋转后,点D旋转到什么位置?请在图中将点D的对应点
D′表示出来.(3).如果AD=1cm,那么点D旋转过的路径是多少?ABCDEF 2、如图,ΔDEF是由△ABC绕某一中心旋转一定的角度得到,请你找出这旋转中心.找旋转中心旋转中心在对应点连线的垂直平分线上。2.在等腰直角△ABC中,∠C=900,BC=2cm,如果以AC的中点O为旋转中心,将这个三角形旋转1800,点B落在点B′处,求BB′的长度.A/B/C/3.已知:如图,在△ABC中,∠BAC=1200,以BC为边向形外作等边三角形△BCD,把△ABD绕着点D按顺时针方向旋转600后得到△ECD,若AB=3,AC=2,求∠BAD的度数与AD的长. 简单的旋转作图练习1
将下图中大写字母N绕它右下侧的顶点按顺时针方向旋转90?,作出旋转后的图案.回顾与小结旋转的定义:在平面内,将一个图形绕一个定点沿着某个方向转动一定的角度,这样的图形运动称为旋转. 这个定点称为旋转中心,转动的角称为旋转角.
旋转的性质:
旋转不改变图形的大小与形状;
旋转前后两图形任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.
旋转的判定方法:利用旋转的性质判定旋转的存在.
旋转的普遍性:旋转广泛存在于我们的生活中.
简单性与复杂性:简单图形旋转的复合可以产生复杂且美妙的图案,可见复杂性蕴藏于简单性之中. 研究旋转的规律可以帮助我们化繁为简,化难为易.谢谢大家
同课章节目录
