4.3 实数(2) 课件(共25张PPT)苏科版数学八年级上册
文档属性
| 名称 | 4.3 实数(2) 课件(共25张PPT)苏科版数学八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 312.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-18 20:56:47 | ||
图片预览







文档简介
(共25张PPT)
实数
第二课时
1.什么叫有理数?
2.什么叫无理数?
复习
3.什么叫实数?
整数和分数统称为有理数。
无限不循环小数称为无理数.
有理数和无理数统称为实数.
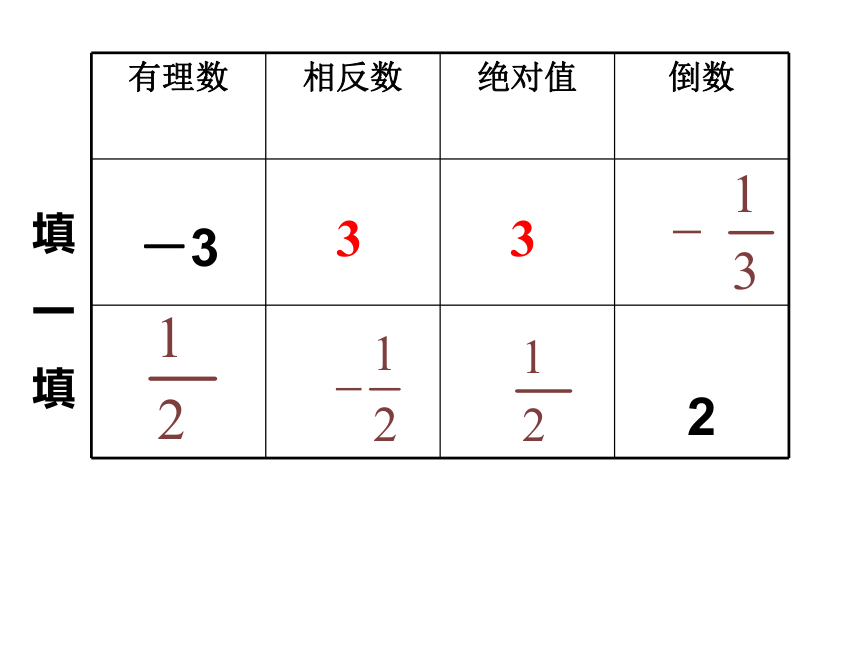
填
一
填
有理数 相反数 绝对值 倒数
-3
2
3
3
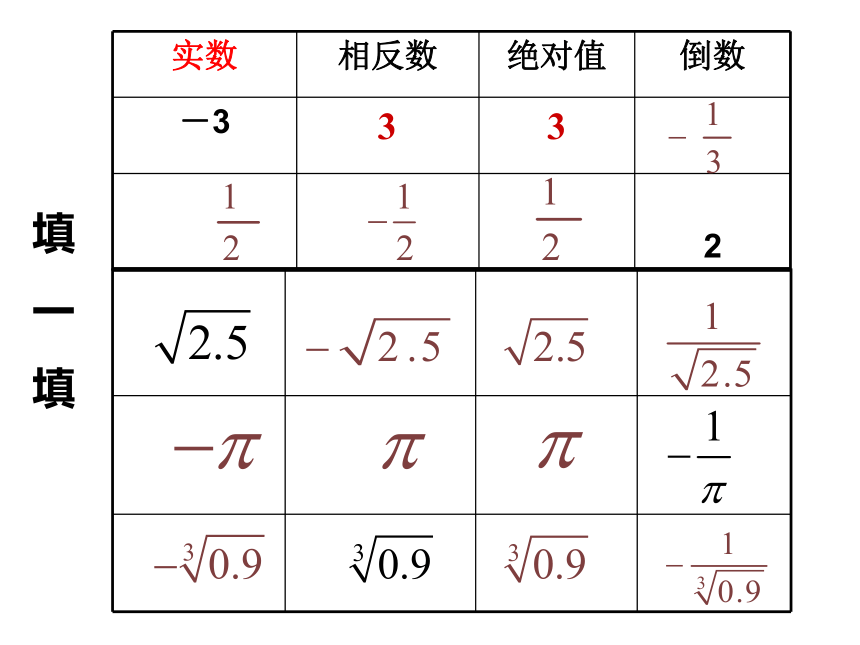
填
一
填
实数 相反数 绝对值 倒数
-3
2
3
3
小结:
在实数范围内,相反数,倒数;绝对值的意义和有理数范围内的相反数,倒数,绝对值的意义完全一样。
实数的四个相关概念:
⑴ 相反数:
a是一个实数:
0的相反数是0
两个互为相反数的数之和为0
的相反数为
a-b的相反数是-(a-b)或b-a
a+b的相反数是-(a+b)或-a-b
实数的四个相关概念:
⑵ 倒数:
两个互为倒数的数之积为1
若
,则
的倒数为
实数的四个相关概念:
⑶ 绝对值:
0
> 0 )
(
(
= 0 )
(
< 0 )
2. 的相反数是______,绝对值是_____.
3. 的相反数是______,绝对值是______.
1.a是一个实数,它的相反数为____;
如果,a≠0那么它的倒数为______.
练习:
4. 的绝对值是__________.
5.已知一个数的绝对值是 ,则这个数是____.
4
练习:
实数的绝对值、相反数、倒数与有理数范围内的意义完全相同,
并且有理数的大小比较的方法、运算性质及运算律在实数范围内仍然适用 .
你能回忆起有理数的大小比较法则吗?
(1)正数都大于零;负数都小于零
正数大于一切负数。
(2)两个正数比较,绝对值大的数大。
(3)两个负数比较,绝对值大的数
反而小
(4)数轴上,右边的点表示的数总比
左边的大。
(4)运算律:
实数满足已经学过的运算律,如:
加法交换律 :a+b=b+a
加法结合律: (a+b)+c=a+(b+c)
乘法交换律: ab=ba
乘法结合律: (ab)c=a(bc)
分配律 : a(b+c)=ab+ac
实数的四个相关概念:
判断题:
(1)任何实数的偶次幂是正实数.
(4)0是绝对值最小的实数.
(3)0是最小的实数.
(2)实数范围内若|x|=|y|,则x=y.
(5)一个实数的平方根有两个.
(6)无理数就是带根号的数.
(7) 是无理数,所以它是无限不循环小数.
√
×
×
×
×
×
√
(1)比较大小:
3 7
<
(2)比较大小:
1.通过估算,比较大小:
﹤
﹥2,所以
﹤2,
因为
2.若a>0,b>0,且a2>b2,则a>b
即因为( )2=3,
( )2=7,所以
﹤
3.利用数轴比较大小.
<
例2
如何估算无理数的大小?
例3
试一试:比较下列各组数的大小:
>
<
=
>
1.怎样比较 与 的大小
(两个负数绝对值大的反而小)
2.怎样比较 0.5 与 的大小
可用平方法,把两个正数都化成带根号或不带根号的式子,从而比较出它们的大小
练习:
②
④
⑤
3.比较下列各组实数的大小
5.绝对值小于 的整数有_____________,
这些整数的和是_______.
0
4.
2或3
6.设m是 的整数部分,n是
的小数部分,
试求m-n的值
1.实数和数轴上的点一一对应的
2.相关概念: 相反数、倒数、绝对值
3.有理数的运算扩充到实数范围内时仍然适用.
4.通过用不同的方法比较两个无理数的大小,如估算法、平方法、作差法、求近似值法等.
★ 0.5即( )与 的分母相同,
所以只要比较1与 的大小.
所以只要比较
与1的大小.
★作差比较
知识延伸
怎样比较 与 的大小
试比较 的大小.
实数
第二课时
1.什么叫有理数?
2.什么叫无理数?
复习
3.什么叫实数?
整数和分数统称为有理数。
无限不循环小数称为无理数.
有理数和无理数统称为实数.
填
一
填
有理数 相反数 绝对值 倒数
-3
2
3
3
填
一
填
实数 相反数 绝对值 倒数
-3
2
3
3
小结:
在实数范围内,相反数,倒数;绝对值的意义和有理数范围内的相反数,倒数,绝对值的意义完全一样。
实数的四个相关概念:
⑴ 相反数:
a是一个实数:
0的相反数是0
两个互为相反数的数之和为0
的相反数为
a-b的相反数是-(a-b)或b-a
a+b的相反数是-(a+b)或-a-b
实数的四个相关概念:
⑵ 倒数:
两个互为倒数的数之积为1
若
,则
的倒数为
实数的四个相关概念:
⑶ 绝对值:
0
> 0 )
(
(
= 0 )
(
< 0 )
2. 的相反数是______,绝对值是_____.
3. 的相反数是______,绝对值是______.
1.a是一个实数,它的相反数为____;
如果,a≠0那么它的倒数为______.
练习:
4. 的绝对值是__________.
5.已知一个数的绝对值是 ,则这个数是____.
4
练习:
实数的绝对值、相反数、倒数与有理数范围内的意义完全相同,
并且有理数的大小比较的方法、运算性质及运算律在实数范围内仍然适用 .
你能回忆起有理数的大小比较法则吗?
(1)正数都大于零;负数都小于零
正数大于一切负数。
(2)两个正数比较,绝对值大的数大。
(3)两个负数比较,绝对值大的数
反而小
(4)数轴上,右边的点表示的数总比
左边的大。
(4)运算律:
实数满足已经学过的运算律,如:
加法交换律 :a+b=b+a
加法结合律: (a+b)+c=a+(b+c)
乘法交换律: ab=ba
乘法结合律: (ab)c=a(bc)
分配律 : a(b+c)=ab+ac
实数的四个相关概念:
判断题:
(1)任何实数的偶次幂是正实数.
(4)0是绝对值最小的实数.
(3)0是最小的实数.
(2)实数范围内若|x|=|y|,则x=y.
(5)一个实数的平方根有两个.
(6)无理数就是带根号的数.
(7) 是无理数,所以它是无限不循环小数.
√
×
×
×
×
×
√
(1)比较大小:
3 7
<
(2)比较大小:
1.通过估算,比较大小:
﹤
﹥2,所以
﹤2,
因为
2.若a>0,b>0,且a2>b2,则a>b
即因为( )2=3,
( )2=7,所以
﹤
3.利用数轴比较大小.
<
例2
如何估算无理数的大小?
例3
试一试:比较下列各组数的大小:
>
<
=
>
1.怎样比较 与 的大小
(两个负数绝对值大的反而小)
2.怎样比较 0.5 与 的大小
可用平方法,把两个正数都化成带根号或不带根号的式子,从而比较出它们的大小
练习:
②
④
⑤
3.比较下列各组实数的大小
5.绝对值小于 的整数有_____________,
这些整数的和是_______.
0
4.
2或3
6.设m是 的整数部分,n是
的小数部分,
试求m-n的值
1.实数和数轴上的点一一对应的
2.相关概念: 相反数、倒数、绝对值
3.有理数的运算扩充到实数范围内时仍然适用.
4.通过用不同的方法比较两个无理数的大小,如估算法、平方法、作差法、求近似值法等.
★ 0.5即( )与 的分母相同,
所以只要比较1与 的大小.
所以只要比较
与1的大小.
★作差比较
知识延伸
怎样比较 与 的大小
试比较 的大小.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
