4.2 立方根 课件(共17张PPT)苏科版数学八年级上册
文档属性
| 名称 | 4.2 立方根 课件(共17张PPT)苏科版数学八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 431.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-18 20:58:36 | ||
图片预览






文档简介
(共17张PPT)
立方根
一、温故而知新
(1) 什么叫一个数a的平方根 如何用符号表示数a(a≥0)
的平方根
(3) 正数有几个平方根 它们之间的关系是什么
负数有没有平方根 0平方根是什么
口答
±
(2) 什么叫一个数a的算术平方根 如何用符号表示数a(a≥0)的算术平方根
情境引入
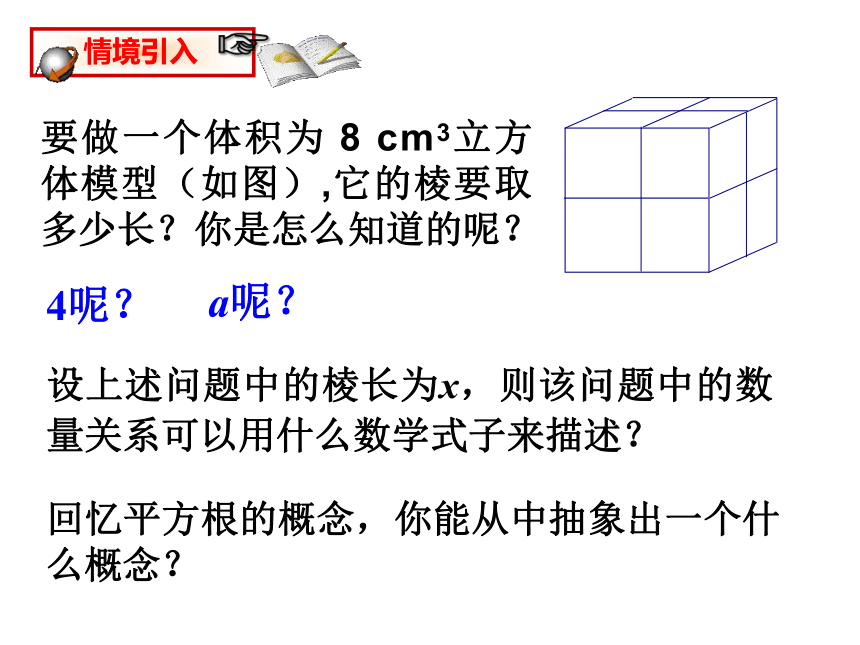
要做一个体积为 8 cm3立方体模型(如图),它的棱要取多少长?你是怎么知道的呢?
4呢?
设上述问题中的棱长为x,则该问题中的数量关系可以用什么数学式子来描述?
a呢?
回忆平方根的概念,你能从中抽象出一个什么概念?
立方根的定义:
如果x3=a,那么x叫做a的立方根,也称为三次方根。
立方根的表示方法:
读作“三次根号a”
a是被开方数,3是根指数(不可省略)
例如:
(1)4的立方是 ,所以4是 的立方根,记作 ;
(2)若53=125,则 称为 的立方根,记作 ;
(3)若x3=2,则 称为 的立方根,记作 。
开立方:求一个数的立方根的运算,叫做开立方。
开平方:求一个数的平方根的运算,叫做
开平方。
例1 求下列各数的立方根:
(1) -27
(2)27
(3)
(4)-0.064
(5) 0
-
练习:求下列各数的立方根:
(1) 1
观察以上算式,想一想:什么数有立方根?
一个正数有几个立方根,负数、0呢?
立方根的性质:
1、正数有一个正的立方根
2、负数有一个负的立方根
3、0的立方根是0
总结:所有实数都有立方根,且一个数的立方根是唯一的,且正负性是一致的.
立方根的性质与平方根性质有何不同
例2 求下例各式的值:
(1)
(2)
(3)
解:
(1)
(2)
(3)
练习:
1.计算:
=-0.1
=-0.1
观察上述式子,你发现了什么?
2.计算:
观察上述式子,你发现了什么?
3.计算:
观察上述式子,你发现了什么?
=
例3 解方程
当堂检测
1. 判断正误:
(1) 的立方根是 ;
(2)互为相反数的立方根互为相反数;
(3)任何数的立方根只有一个;
(4)如果一个数的平方根与其立方根相同,则 这个数是1;
(5)如果一个数的立方根是这个数的本身,那么这个数一定是零;
(6)一个数的立方根不是正数就是负数.
(×)
(×)
(×)
(×)
( √ )
( √ )
4
-7
2.填空:
(1) 64的平方根是________, 算术平方根是 ,
64的立方根是________.
(2) 的立方根是________, 的平方根是________.
(3) 是_______的立方根.
(4) 的立方根是________, 的平方根是________.
±8
8
±2
2
小结:
1、平方根的定义:如果一个数的平方等于a,那么这个数就叫做a是平方根
a的平方根用±
2、平方根的性质
(1)一个正数有两个平方根,它们互为相反数
(2)0的平方根还是0
(3)负数没有平方根
3、平方根的求法:
如求4的平方根:
∵ (±2)2 = 4
∴4的平方根是±2
即
1、立方根的定义:如果一个数的立方等于a,那么这个数叫做a的立方根
a的立方根用 表示
2、立方根的性质
(1)正数的立方根还是正数
(2)0的立方根还是0
(3)负数的立方根还是负数
3、立方根的求法:
如求8的立方根:
∵ 23 = 8
∴8的立方根是2
即
立方根
一、温故而知新
(1) 什么叫一个数a的平方根 如何用符号表示数a(a≥0)
的平方根
(3) 正数有几个平方根 它们之间的关系是什么
负数有没有平方根 0平方根是什么
口答
±
(2) 什么叫一个数a的算术平方根 如何用符号表示数a(a≥0)的算术平方根
情境引入
要做一个体积为 8 cm3立方体模型(如图),它的棱要取多少长?你是怎么知道的呢?
4呢?
设上述问题中的棱长为x,则该问题中的数量关系可以用什么数学式子来描述?
a呢?
回忆平方根的概念,你能从中抽象出一个什么概念?
立方根的定义:
如果x3=a,那么x叫做a的立方根,也称为三次方根。
立方根的表示方法:
读作“三次根号a”
a是被开方数,3是根指数(不可省略)
例如:
(1)4的立方是 ,所以4是 的立方根,记作 ;
(2)若53=125,则 称为 的立方根,记作 ;
(3)若x3=2,则 称为 的立方根,记作 。
开立方:求一个数的立方根的运算,叫做开立方。
开平方:求一个数的平方根的运算,叫做
开平方。
例1 求下列各数的立方根:
(1) -27
(2)27
(3)
(4)-0.064
(5) 0
-
练习:求下列各数的立方根:
(1) 1
观察以上算式,想一想:什么数有立方根?
一个正数有几个立方根,负数、0呢?
立方根的性质:
1、正数有一个正的立方根
2、负数有一个负的立方根
3、0的立方根是0
总结:所有实数都有立方根,且一个数的立方根是唯一的,且正负性是一致的.
立方根的性质与平方根性质有何不同
例2 求下例各式的值:
(1)
(2)
(3)
解:
(1)
(2)
(3)
练习:
1.计算:
=-0.1
=-0.1
观察上述式子,你发现了什么?
2.计算:
观察上述式子,你发现了什么?
3.计算:
观察上述式子,你发现了什么?
=
例3 解方程
当堂检测
1. 判断正误:
(1) 的立方根是 ;
(2)互为相反数的立方根互为相反数;
(3)任何数的立方根只有一个;
(4)如果一个数的平方根与其立方根相同,则 这个数是1;
(5)如果一个数的立方根是这个数的本身,那么这个数一定是零;
(6)一个数的立方根不是正数就是负数.
(×)
(×)
(×)
(×)
( √ )
( √ )
4
-7
2.填空:
(1) 64的平方根是________, 算术平方根是 ,
64的立方根是________.
(2) 的立方根是________, 的平方根是________.
(3) 是_______的立方根.
(4) 的立方根是________, 的平方根是________.
±8
8
±2
2
小结:
1、平方根的定义:如果一个数的平方等于a,那么这个数就叫做a是平方根
a的平方根用±
2、平方根的性质
(1)一个正数有两个平方根,它们互为相反数
(2)0的平方根还是0
(3)负数没有平方根
3、平方根的求法:
如求4的平方根:
∵ (±2)2 = 4
∴4的平方根是±2
即
1、立方根的定义:如果一个数的立方等于a,那么这个数叫做a的立方根
a的立方根用 表示
2、立方根的性质
(1)正数的立方根还是正数
(2)0的立方根还是0
(3)负数的立方根还是负数
3、立方根的求法:
如求8的立方根:
∵ 23 = 8
∴8的立方根是2
即
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
