第一单元圆必考题检测卷(单元测试)数学六年级上册北师大版(含答案)
文档属性
| 名称 | 第一单元圆必考题检测卷(单元测试)数学六年级上册北师大版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-18 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第一单元圆必考题检测卷(单元测试)数学六年级上册北师大版
一、选择题
1.用一条长12.56厘米的铁丝围成下面四种图形,面积最大的是( )。
A.圆 B.正方形 C.长方形 D.三角形
2.一个边长是4cm的正方形画一个最大的圆,周长是( )cm。
A.12.56 B.16 C.25.12
3.经过1小时,钟面上分针转过的角度与时针转过的角度相差( )。
A.150° B.300° C.330° D.100°
4.如图中阴影部分的周长相比( )。
A.甲的周长>乙的周长 B.甲的周长<乙的周长
C.甲、乙周长相等 D.无法比较
5.一根铁丝正好围成一个直径是8cm的圆,如果围成正方形,它的边长是( )。
A.3.14 B.6.28 C.12.56 D.25.12
6.圆的半径由4cm增加到12cm,圆的周长增加了( )cm。
A.π B.8π C.12π D.16π
二、填空题
7.圆的半径是3厘米,直径是( )厘米,周长是( )厘米,面积是( )平方厘米。
8.在一个边长为10cm的正方形中画一个最大的圆,这个图形有( )条对称轴。正方形中这个最大圆的周长是( )cm。
9.如图,把一个半径是6厘米的圆分成若干等份后剪开,再拼成一个近似的长方形,拼成的图形的宽约是( )厘米,长约是( )厘米。
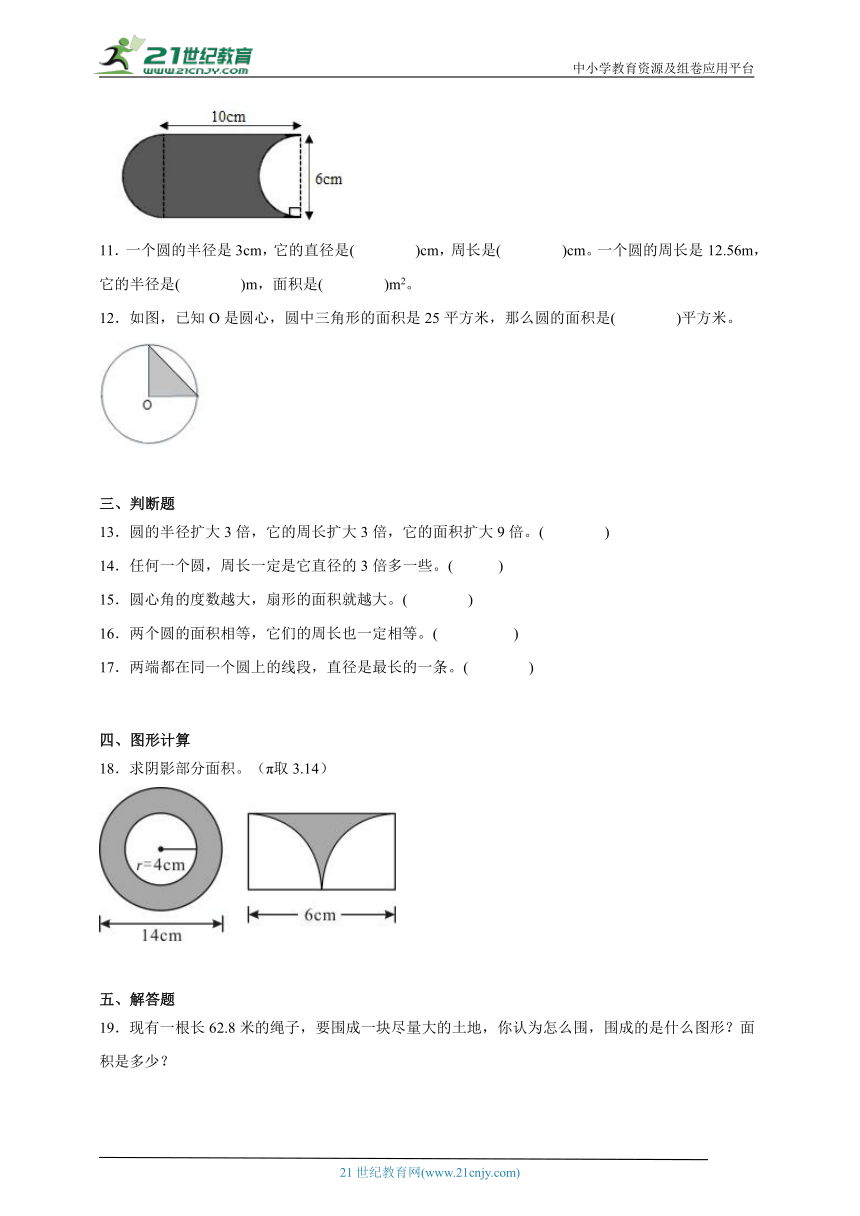
10.如图,阴影部分的面积是( )平方厘米,周长是( )厘米。
11.一个圆的半径是3cm,它的直径是( )cm,周长是( )cm。一个圆的周长是12.56m,它的半径是( )m,面积是( )m2。
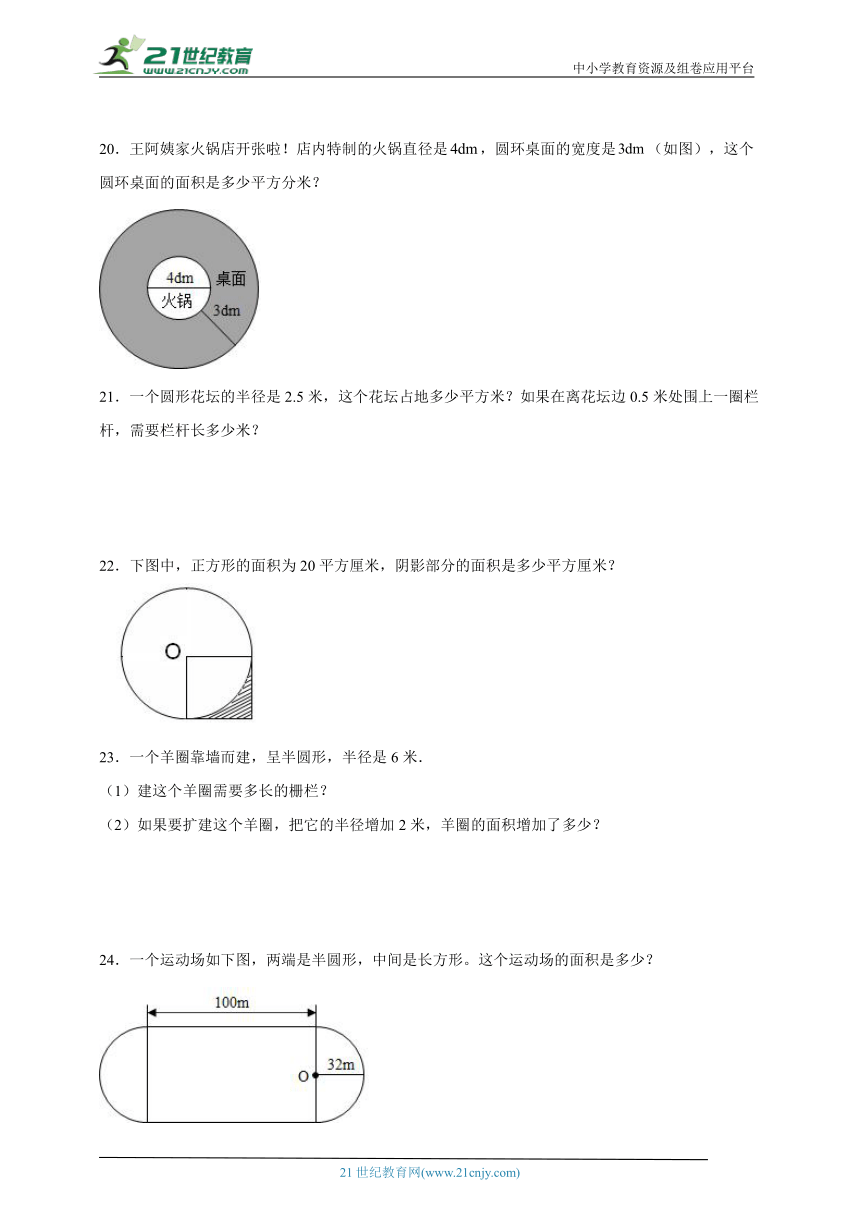
12.如图,已知O是圆心,圆中三角形的面积是25平方米,那么圆的面积是( )平方米。
三、判断题
13.圆的半径扩大3倍,它的周长扩大3倍,它的面积扩大9倍。( )
14.任何一个圆,周长一定是它直径的3倍多一些。( )
15.圆心角的度数越大,扇形的面积就越大。( )
16.两个圆的面积相等,它们的周长也一定相等。( )
17.两端都在同一个圆上的线段,直径是最长的一条。( )
四、图形计算
18.求阴影部分面积。(π取3.14)
五、解答题
19.现有一根长62.8米的绳子,要围成一块尽量大的土地,你认为怎么围,围成的是什么图形?面积是多少?
20.王阿姨家火锅店开张啦!店内特制的火锅直径是,圆环桌面的宽度是(如图),这个圆环桌面的面积是多少平方分米?
21.一个圆形花坛的半径是2.5米,这个花坛占地多少平方米?如果在离花坛边0.5米处围上一圈栏杆,需要栏杆长多少米?
22.下图中,正方形的面积为20平方厘米,阴影部分的面积是多少平方厘米?
23.一个羊圈靠墙而建,呈半圆形,半径是6米.
(1)建这个羊圈需要多长的栅栏?
(2)如果要扩建这个羊圈,把它的半径增加2米,羊圈的面积增加了多少?
24.一个运动场如下图,两端是半圆形,中间是长方形。这个运动场的面积是多少?
参考答案:
1.A
【分析】根据题意,可利用正方形、长方形、三角形、圆的周长公式,分别计算出它们的边长或半径,然后再依据面积公式计算出这些图形的面积,然后比较大小即可得到答案。
【详解】正方形的边长是:12.56÷4=3.14(厘米)
正方形的面积是:3.14×3.14=9.8596(平方厘米);
长方形的长和宽的和是:12.56÷2=6.28(厘米)
长和宽越接近面积越大,长可为3.15厘米,宽为3.13厘米,
长方形的面积是:3.15×3.13=9.8595(平方厘米);
假设是正三角形,其边长是:12.56÷3=4.2(厘米)
三角形的高小于斜边,所以三角形的面积就小于4.2×4.2÷2=8.82(平方厘米);
圆的半径是:12.56÷2÷3.14=2(厘米)
圆的面积是:2×2×3.14=12.56(平方厘米);
8.82<9.8595<9.8596<12.56;
所以围成的圆的面积最大。
故答案为:A
【点睛】在周长一定的情况下,所围成的平面图形的面积从大到小依次是圆、正方形、长方形、三角形,即越接近圆面积越大。
2.A
【分析】正方形内画一个最大的圆,圆的直径=正方形边长,根据圆的周长=πd,列式计算即可。
【详解】3.14×4=12.56(cm)
故答案为:A
【点睛】关键是理解正方形和圆之间的关系,掌握圆的周长公式。
3.C
【分析】钟面上12个数字把钟面平均分成12大格,每大格所对应的圆心角是360°÷12=30°,每两个相邻数字间的夹角是30°。经过1小时,时针转过了30°,分针转过了一圈,即360°,据此即可计算出经过1小时,钟面上分针转过的角度与时针转过的角度相差多少度。
【详解】360°-30°=330°
故答案为:C
【点睛】解答题的关键是弄清1小时时针、分针旋转的度数。
4.A
【分析】甲中的半圆和乙中的四分之一的圆的半径相同,假设正方形的边长为2厘米,甲图阴影部分的周长:两个半圆的周长+两条正方形的边长;乙图阴影部分的周长=4个四分之一的圆的周长,分别算出两个阴影部分的周长,再比较即可。
【详解】正方形的边长为2厘米
甲图阴影部分的周长:2+2+2=(2+4)厘米
乙图阴影部分的周长:2厘米
所以甲的周长>乙的周长。
故答案为:A
【点睛】圆的周长=直径×,据此解答即可。
5.B
【分析】根据圆的周长公式:C=πd,把数据代入公式求出这根铁丝的长度,再根据正方形的周长公式:C=4a,那么a=C÷4,把数据代入公式解答。
【详解】3.14×8÷4
=25.12÷4
=6.28(厘米)
故答案为:B
【点睛】此题主要考查圆的周长公式、正方形的周长公式的灵活运用,关键是熟记公式。
6.D
【分析】根据圆的周长公式:C=2πr,把数据代入公式求出两个圆的周长差即可。
【详解】2×π×12-2×π×4
=24π-8π
=16π(厘米)
圆的周长增加了16π厘米。
故答案为:D
【点睛】此题主要考查圆的周长公式的灵活运用,关键是熟记公式。
7. 6 18.84 28.26
【分析】在同一个圆中直径是半径的2倍,利用求出圆的周长,利用求出圆的面积,据此解答。
【详解】直径:3×2=6(厘米)
周长:6×3.14=18.84(厘米)
面积:3.14×3×3
=9.42×3
=28.26(平方厘米)
【点睛】掌握圆的周长和面积计算公式是解答题目的关键。
8. 4 31.4
【分析】轴对称图形定义为平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形,直线叫做对称轴。
正方形中这个最大圆的直径=正方形边长,根据圆的周长=πd,求出圆的周长。
【详解】
3.14×10=31.4(厘米)
这个图形有4条对称轴。正方形中这个最大圆的周长是31.4cm。
【点睛】关键是熟悉轴对称图形的特点,掌握圆的周长公式。
9. 6 18.84
【分析】把圆平均分的份数越多,拼成的图形就会越接近于一个长方形,把一个半径是6厘米的圆分成若干等份后剪开,再拼成一个近似的长方形,宽近似于圆的半径,长近似于圆的周长的一半,可据此解答。
【详解】近似于长方形的宽约:6厘米;
近似于长方形的长约:
3.14×6×2÷2
=3.14×6×(2÷2)
=3.14×6
=18.84(厘米)
【点睛】理解圆的面积推导过程是解此题的关键。
10. 60 38.84
【分析】把这个不规则的图形用分割法沿着半圆的直径分开,把这个半圆平移到不规则图形的右边,组成一个长为10㎝、宽为6㎝的长方形,这个长方形的面积等于阴影部分的面积;阴影部分的周长是由长方形两条长为10厘米和一个直径为6厘米的圆的周长组成的,可据此解答。
【详解】阴影部分的面积:
10×6=60(平方厘米)
阴影部分的周长:
10×2+3.14×6
=20+18.84
=38.84(厘米)
【点睛】求不规则图形的面积或周长时要善于观察,利用分割、补全、平移的方法化繁为简,是解决此类问题的关键。
11. 6 18.84 2 12.56
【分析】(1)在同一个圆中,直径是半径的2倍,利用圆的周长公式:,求出圆的周长;
(2)利用圆的周长公式求出圆的半径,再利用圆的面积公式:,即可求得。
【详解】(1)直径:3×2=6(厘米)
周长:3.14×6=18.84(厘米)
(2)半径:12.56÷3.14÷2
=4÷2
=2(米)
面积:3.14×22=12.56(平方米)
【点睛】灵活运用圆的周长和面积计算公式是解答题目的关键。
12.157
【分析】根据图意可知,三角形的面积等于圆的半径2÷2,所以圆的半径2=25×2=50,再将这一数据代入圆的面积公式计算即可解答。
【详解】3.14×(25×2)
=3.14×50
=157(平方米)
【点睛】本题主要考查圆的面积公式与三角形的面积公式,熟练掌握两个公式是解答本题的关键。
13.√
【分析】假设出原来圆的半径,计算出扩大之后圆的半径,表示出圆的周长和半径,最后分析周长和面积的变化情况。
【详解】假设原来圆的半径为1厘米
半径:1×3=3(厘米)
周长:(2××3)÷(2××1)
=6÷2
=3
面积:(×32)÷(×12)
=9÷
=9
所以,圆的半径扩大3倍,它的周长扩大3倍,它的面积扩大9倍。
故答案为:√
【点睛】圆的半径扩大到原来的倍,圆的周长扩大到原来的倍,圆的面积扩大到原来的倍。
14.√
【分析】根据圆的周长与直径的关系解答即可。
【详解】任何一个圆,周长一定是它直径的3倍多一些,说法正确。
故答案为:√。
【点睛】本题考查圆的周长,解答本题的关键是掌握圆的周长概念。
15.×
【分析】在同圆或等圆中,圆心角越大所对应的弧线越长,得到的扇形的面积越大,圆心角越小所对应的弧线越短,扇形的面积越小,据此判断即可。
【详解】在同圆或等圆中,圆心角的度数越大,扇形的面积就越大,原题说法错误;
故答案为:×。
【点睛】熟练掌握有关圆心角的基础知识是解答本题的关键。
16.√
【分析】圆的面积与半径有关,当两个圆的面积相等时,它们的半径和直径都相等,所以周长也相等,据此解答即可。
【详解】两个圆的面积相等,它们的周长也一定相等,原题说法正确;
故答案为:√
【点睛】熟练掌握圆的周长和面积公式是解答本题的关键。
17.√
【分析】通过圆心并且两端都在圆上的线段叫做圆的直径,直径是圆中最长的线段,在同一个圆内有无数条直径,据此解答。
【详解】
由图可知,两端都在同一个圆上的线段,直径是最长的一条。
故答案为:√
【点睛】掌握圆的特征是解答题目的关键。
18.103.62cm2;3.87cm2
【分析】(1)根据圆环的面积S=π(R2-r2),代入相应的数据进行计算即可。
(2)阴影部分面积=长方形的面积-半圆的面积,代入相应的数据进行计算即可。
【详解】(1)
=
=
=103.62(cm2)
(2)
=
=
=3.87(cm2)
19.把绳子围成圆形面积最大;314平方米
【分析】根据在所有的平面图形中,周长一定围成了圆的面积最大,所以可以把这根绳子围成一个圆形,然后再根据圆的周长公式C=2πr,得出圆的半径r=C÷π÷2,最后再根据圆的面积公式:S=πr2进行计算即可得到答案。
【详解】围成圆的半径为:62.8÷3.14÷2=10(米)
围成圆的面积为:3.14×102=314(平方米)
答:把绳子围成圆形面积最大,面积是314平方米。
【点睛】此题主要考查的是在所有的平面图形中,周长一定围成的圆的面积最大,然后再灵活利用圆的周长公式和圆的面积公式进行计算即可。
20.65.94平方分米
【分析】由图可知,大圆半径为(4÷2+3)分米,小圆半径为(4÷2)分米,利用圆环的面积公式: ,即可求得。
【详解】大圆半径:4÷2+3
=2+3
=5(分米)
小圆半径:4÷2=2(分米)
3.14×(52-22)
=3.14×21
=65.94(平方分米)
答:这个圆环桌面的面积是65.94平方分米。
【点睛】掌握环形的面积计算公式是解答题目的关键。
21.19.625平方米;18.84米
【分析】求占地面积就是求圆的面积,圆的面积=πr ;围成的栏杆长度相当于求圆的周长,半径=2.5+0.5=3米,圆的周长=2πr,代入数据计算即可求解。
【详解】3.14×2.5
=3.14×6.25
=19.625(平方米)
3.14×(2.5+0.5)×2
=3.14×3×2
=18.84(米)
答:花坛的占地面积是19.625平方米,栏杆的长度是18.84米。
【点睛】此题考查圆的周长公式和面积公式。
22.20-3.14×20×=4.3cm2
【详解】略
23.(1)18.84米
(2)43.96平方米
【详解】(1)2×3.14×6÷2=18.84(米)
答:建这个羊圈需要18.84米长的栅栏.
(2)6+2=8(米)
3.14×(82﹣62)÷2
=3.14(64﹣36)÷2
=3.14×28÷2
=43.96(平方米)
答:羊圈的面积增加了43.96平方米
24.9615.36平方米
【分析】根据题图可知,运动场的面积包括圆的面积和长方形的面积,据此解答即可
【详解】100×(32×2)+3.14×32
=6400+3215.36
=9615.36(平方米);
答:这个运动场的面积是9615.36平方米。
【点睛】明确“组合图形的面积=圆的面积+长方形的面积”是解答本题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第一单元圆必考题检测卷(单元测试)数学六年级上册北师大版
一、选择题
1.用一条长12.56厘米的铁丝围成下面四种图形,面积最大的是( )。
A.圆 B.正方形 C.长方形 D.三角形
2.一个边长是4cm的正方形画一个最大的圆,周长是( )cm。
A.12.56 B.16 C.25.12
3.经过1小时,钟面上分针转过的角度与时针转过的角度相差( )。
A.150° B.300° C.330° D.100°
4.如图中阴影部分的周长相比( )。
A.甲的周长>乙的周长 B.甲的周长<乙的周长
C.甲、乙周长相等 D.无法比较
5.一根铁丝正好围成一个直径是8cm的圆,如果围成正方形,它的边长是( )。
A.3.14 B.6.28 C.12.56 D.25.12
6.圆的半径由4cm增加到12cm,圆的周长增加了( )cm。
A.π B.8π C.12π D.16π
二、填空题
7.圆的半径是3厘米,直径是( )厘米,周长是( )厘米,面积是( )平方厘米。
8.在一个边长为10cm的正方形中画一个最大的圆,这个图形有( )条对称轴。正方形中这个最大圆的周长是( )cm。
9.如图,把一个半径是6厘米的圆分成若干等份后剪开,再拼成一个近似的长方形,拼成的图形的宽约是( )厘米,长约是( )厘米。
10.如图,阴影部分的面积是( )平方厘米,周长是( )厘米。
11.一个圆的半径是3cm,它的直径是( )cm,周长是( )cm。一个圆的周长是12.56m,它的半径是( )m,面积是( )m2。
12.如图,已知O是圆心,圆中三角形的面积是25平方米,那么圆的面积是( )平方米。
三、判断题
13.圆的半径扩大3倍,它的周长扩大3倍,它的面积扩大9倍。( )
14.任何一个圆,周长一定是它直径的3倍多一些。( )
15.圆心角的度数越大,扇形的面积就越大。( )
16.两个圆的面积相等,它们的周长也一定相等。( )
17.两端都在同一个圆上的线段,直径是最长的一条。( )
四、图形计算
18.求阴影部分面积。(π取3.14)
五、解答题
19.现有一根长62.8米的绳子,要围成一块尽量大的土地,你认为怎么围,围成的是什么图形?面积是多少?
20.王阿姨家火锅店开张啦!店内特制的火锅直径是,圆环桌面的宽度是(如图),这个圆环桌面的面积是多少平方分米?
21.一个圆形花坛的半径是2.5米,这个花坛占地多少平方米?如果在离花坛边0.5米处围上一圈栏杆,需要栏杆长多少米?
22.下图中,正方形的面积为20平方厘米,阴影部分的面积是多少平方厘米?
23.一个羊圈靠墙而建,呈半圆形,半径是6米.
(1)建这个羊圈需要多长的栅栏?
(2)如果要扩建这个羊圈,把它的半径增加2米,羊圈的面积增加了多少?
24.一个运动场如下图,两端是半圆形,中间是长方形。这个运动场的面积是多少?
参考答案:
1.A
【分析】根据题意,可利用正方形、长方形、三角形、圆的周长公式,分别计算出它们的边长或半径,然后再依据面积公式计算出这些图形的面积,然后比较大小即可得到答案。
【详解】正方形的边长是:12.56÷4=3.14(厘米)
正方形的面积是:3.14×3.14=9.8596(平方厘米);
长方形的长和宽的和是:12.56÷2=6.28(厘米)
长和宽越接近面积越大,长可为3.15厘米,宽为3.13厘米,
长方形的面积是:3.15×3.13=9.8595(平方厘米);
假设是正三角形,其边长是:12.56÷3=4.2(厘米)
三角形的高小于斜边,所以三角形的面积就小于4.2×4.2÷2=8.82(平方厘米);
圆的半径是:12.56÷2÷3.14=2(厘米)
圆的面积是:2×2×3.14=12.56(平方厘米);
8.82<9.8595<9.8596<12.56;
所以围成的圆的面积最大。
故答案为:A
【点睛】在周长一定的情况下,所围成的平面图形的面积从大到小依次是圆、正方形、长方形、三角形,即越接近圆面积越大。
2.A
【分析】正方形内画一个最大的圆,圆的直径=正方形边长,根据圆的周长=πd,列式计算即可。
【详解】3.14×4=12.56(cm)
故答案为:A
【点睛】关键是理解正方形和圆之间的关系,掌握圆的周长公式。
3.C
【分析】钟面上12个数字把钟面平均分成12大格,每大格所对应的圆心角是360°÷12=30°,每两个相邻数字间的夹角是30°。经过1小时,时针转过了30°,分针转过了一圈,即360°,据此即可计算出经过1小时,钟面上分针转过的角度与时针转过的角度相差多少度。
【详解】360°-30°=330°
故答案为:C
【点睛】解答题的关键是弄清1小时时针、分针旋转的度数。
4.A
【分析】甲中的半圆和乙中的四分之一的圆的半径相同,假设正方形的边长为2厘米,甲图阴影部分的周长:两个半圆的周长+两条正方形的边长;乙图阴影部分的周长=4个四分之一的圆的周长,分别算出两个阴影部分的周长,再比较即可。
【详解】正方形的边长为2厘米
甲图阴影部分的周长:2+2+2=(2+4)厘米
乙图阴影部分的周长:2厘米
所以甲的周长>乙的周长。
故答案为:A
【点睛】圆的周长=直径×,据此解答即可。
5.B
【分析】根据圆的周长公式:C=πd,把数据代入公式求出这根铁丝的长度,再根据正方形的周长公式:C=4a,那么a=C÷4,把数据代入公式解答。
【详解】3.14×8÷4
=25.12÷4
=6.28(厘米)
故答案为:B
【点睛】此题主要考查圆的周长公式、正方形的周长公式的灵活运用,关键是熟记公式。
6.D
【分析】根据圆的周长公式:C=2πr,把数据代入公式求出两个圆的周长差即可。
【详解】2×π×12-2×π×4
=24π-8π
=16π(厘米)
圆的周长增加了16π厘米。
故答案为:D
【点睛】此题主要考查圆的周长公式的灵活运用,关键是熟记公式。
7. 6 18.84 28.26
【分析】在同一个圆中直径是半径的2倍,利用求出圆的周长,利用求出圆的面积,据此解答。
【详解】直径:3×2=6(厘米)
周长:6×3.14=18.84(厘米)
面积:3.14×3×3
=9.42×3
=28.26(平方厘米)
【点睛】掌握圆的周长和面积计算公式是解答题目的关键。
8. 4 31.4
【分析】轴对称图形定义为平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形,直线叫做对称轴。
正方形中这个最大圆的直径=正方形边长,根据圆的周长=πd,求出圆的周长。
【详解】
3.14×10=31.4(厘米)
这个图形有4条对称轴。正方形中这个最大圆的周长是31.4cm。
【点睛】关键是熟悉轴对称图形的特点,掌握圆的周长公式。
9. 6 18.84
【分析】把圆平均分的份数越多,拼成的图形就会越接近于一个长方形,把一个半径是6厘米的圆分成若干等份后剪开,再拼成一个近似的长方形,宽近似于圆的半径,长近似于圆的周长的一半,可据此解答。
【详解】近似于长方形的宽约:6厘米;
近似于长方形的长约:
3.14×6×2÷2
=3.14×6×(2÷2)
=3.14×6
=18.84(厘米)
【点睛】理解圆的面积推导过程是解此题的关键。
10. 60 38.84
【分析】把这个不规则的图形用分割法沿着半圆的直径分开,把这个半圆平移到不规则图形的右边,组成一个长为10㎝、宽为6㎝的长方形,这个长方形的面积等于阴影部分的面积;阴影部分的周长是由长方形两条长为10厘米和一个直径为6厘米的圆的周长组成的,可据此解答。
【详解】阴影部分的面积:
10×6=60(平方厘米)
阴影部分的周长:
10×2+3.14×6
=20+18.84
=38.84(厘米)
【点睛】求不规则图形的面积或周长时要善于观察,利用分割、补全、平移的方法化繁为简,是解决此类问题的关键。
11. 6 18.84 2 12.56
【分析】(1)在同一个圆中,直径是半径的2倍,利用圆的周长公式:,求出圆的周长;
(2)利用圆的周长公式求出圆的半径,再利用圆的面积公式:,即可求得。
【详解】(1)直径:3×2=6(厘米)
周长:3.14×6=18.84(厘米)
(2)半径:12.56÷3.14÷2
=4÷2
=2(米)
面积:3.14×22=12.56(平方米)
【点睛】灵活运用圆的周长和面积计算公式是解答题目的关键。
12.157
【分析】根据图意可知,三角形的面积等于圆的半径2÷2,所以圆的半径2=25×2=50,再将这一数据代入圆的面积公式计算即可解答。
【详解】3.14×(25×2)
=3.14×50
=157(平方米)
【点睛】本题主要考查圆的面积公式与三角形的面积公式,熟练掌握两个公式是解答本题的关键。
13.√
【分析】假设出原来圆的半径,计算出扩大之后圆的半径,表示出圆的周长和半径,最后分析周长和面积的变化情况。
【详解】假设原来圆的半径为1厘米
半径:1×3=3(厘米)
周长:(2××3)÷(2××1)
=6÷2
=3
面积:(×32)÷(×12)
=9÷
=9
所以,圆的半径扩大3倍,它的周长扩大3倍,它的面积扩大9倍。
故答案为:√
【点睛】圆的半径扩大到原来的倍,圆的周长扩大到原来的倍,圆的面积扩大到原来的倍。
14.√
【分析】根据圆的周长与直径的关系解答即可。
【详解】任何一个圆,周长一定是它直径的3倍多一些,说法正确。
故答案为:√。
【点睛】本题考查圆的周长,解答本题的关键是掌握圆的周长概念。
15.×
【分析】在同圆或等圆中,圆心角越大所对应的弧线越长,得到的扇形的面积越大,圆心角越小所对应的弧线越短,扇形的面积越小,据此判断即可。
【详解】在同圆或等圆中,圆心角的度数越大,扇形的面积就越大,原题说法错误;
故答案为:×。
【点睛】熟练掌握有关圆心角的基础知识是解答本题的关键。
16.√
【分析】圆的面积与半径有关,当两个圆的面积相等时,它们的半径和直径都相等,所以周长也相等,据此解答即可。
【详解】两个圆的面积相等,它们的周长也一定相等,原题说法正确;
故答案为:√
【点睛】熟练掌握圆的周长和面积公式是解答本题的关键。
17.√
【分析】通过圆心并且两端都在圆上的线段叫做圆的直径,直径是圆中最长的线段,在同一个圆内有无数条直径,据此解答。
【详解】
由图可知,两端都在同一个圆上的线段,直径是最长的一条。
故答案为:√
【点睛】掌握圆的特征是解答题目的关键。
18.103.62cm2;3.87cm2
【分析】(1)根据圆环的面积S=π(R2-r2),代入相应的数据进行计算即可。
(2)阴影部分面积=长方形的面积-半圆的面积,代入相应的数据进行计算即可。
【详解】(1)
=
=
=103.62(cm2)
(2)
=
=
=3.87(cm2)
19.把绳子围成圆形面积最大;314平方米
【分析】根据在所有的平面图形中,周长一定围成了圆的面积最大,所以可以把这根绳子围成一个圆形,然后再根据圆的周长公式C=2πr,得出圆的半径r=C÷π÷2,最后再根据圆的面积公式:S=πr2进行计算即可得到答案。
【详解】围成圆的半径为:62.8÷3.14÷2=10(米)
围成圆的面积为:3.14×102=314(平方米)
答:把绳子围成圆形面积最大,面积是314平方米。
【点睛】此题主要考查的是在所有的平面图形中,周长一定围成的圆的面积最大,然后再灵活利用圆的周长公式和圆的面积公式进行计算即可。
20.65.94平方分米
【分析】由图可知,大圆半径为(4÷2+3)分米,小圆半径为(4÷2)分米,利用圆环的面积公式: ,即可求得。
【详解】大圆半径:4÷2+3
=2+3
=5(分米)
小圆半径:4÷2=2(分米)
3.14×(52-22)
=3.14×21
=65.94(平方分米)
答:这个圆环桌面的面积是65.94平方分米。
【点睛】掌握环形的面积计算公式是解答题目的关键。
21.19.625平方米;18.84米
【分析】求占地面积就是求圆的面积,圆的面积=πr ;围成的栏杆长度相当于求圆的周长,半径=2.5+0.5=3米,圆的周长=2πr,代入数据计算即可求解。
【详解】3.14×2.5
=3.14×6.25
=19.625(平方米)
3.14×(2.5+0.5)×2
=3.14×3×2
=18.84(米)
答:花坛的占地面积是19.625平方米,栏杆的长度是18.84米。
【点睛】此题考查圆的周长公式和面积公式。
22.20-3.14×20×=4.3cm2
【详解】略
23.(1)18.84米
(2)43.96平方米
【详解】(1)2×3.14×6÷2=18.84(米)
答:建这个羊圈需要18.84米长的栅栏.
(2)6+2=8(米)
3.14×(82﹣62)÷2
=3.14(64﹣36)÷2
=3.14×28÷2
=43.96(平方米)
答:羊圈的面积增加了43.96平方米
24.9615.36平方米
【分析】根据题图可知,运动场的面积包括圆的面积和长方形的面积,据此解答即可
【详解】100×(32×2)+3.14×32
=6400+3215.36
=9615.36(平方米);
答:这个运动场的面积是9615.36平方米。
【点睛】明确“组合图形的面积=圆的面积+长方形的面积”是解答本题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
