2023-2024学年沪科版九年级数学上册第21章二次函数与反比例函数 解答题专题训练(含答案)
文档属性
| 名称 | 2023-2024学年沪科版九年级数学上册第21章二次函数与反比例函数 解答题专题训练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 731.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-19 16:36:24 | ||
图片预览



文档简介
2023-2024学年沪科版九年级数学上册《第21章二次函数与反比例函数》
解答题专题训练(附答案)
1.如图,已知一次函数y1=k1x+b的图象与反比例函数y2=,分别交于点A和点B,且A、B两点的坐标分别是A(﹣1,﹣2)和B(2.m),连接OA、OB.
(1)求一次函数y1=k1x+b与反比例函数y2=的函数表达式;
(2)求△AOB的面积.
2.如图,在平面直角坐标系中,抛物线C1:y=(x+m)(x﹣m﹣2)与x轴交于点A和点B,顶点为C.
(1)求抛物线C1的对称轴;
(2)若抛物线C1经过点(0,﹣8),求m的值;
(3)在(2)的条件下,将抛物线C1向上平移至抛物线C2,此时抛物线C2的顶点D恰好是△ABC的重心,求抛物线C2的函数表达式.
3.如图,Rt△OAB的直角顶点B在x轴的正半轴上,点A在第一象限内,已知反比例函数(x>0)的图象经过线段OA的中点D,交直线AB于点C.若△OAB的面积为6.
(1)求k的值;
(2)若AC=OB,求点A的坐标.
4.某工厂生产一种产品,经市场调查发现,该产品每月的销售量y(件)与售价x(万元/件)之间满足一次函数关系,部分数据如表:
每件售价x/万元 … 24 26 28 30 32 …
月销售量y/件 … 52 48 44 40 36 …
(1)求y与x的函数关系式(不写自变量的取值范围).
(2)该产品今年三月份的售价为35万元/件,利润为450万元.
①求:三月份每件产品的成本是多少万元?
②四月份工厂为了降低成本,提高产品质量,投资了450万元改进设备和革新技术,使每件产品的成本比三月份下降了14万元.若四月份每件产品的售价至少为25万元,且不高于30万元,求这个月获得的利润w(万元)关于售价x(万元/件)的函数关系式,并求最少利润是多少万元.
5.如图,直线y=2x与双曲线y=(x>0,k>0)相交于点A,AB⊥x轴于点B,以AB为边在右侧作正方形ABCD,CD与双曲线相交于点E,连接AE、OE.
(1)当BC=4时,求点E的坐标;
(2)当S△AOE=24时,求k的值;
(3)是否存在实数k,满足AE⊥OA,若存在,求出k的值;若不存在,请说明理由.
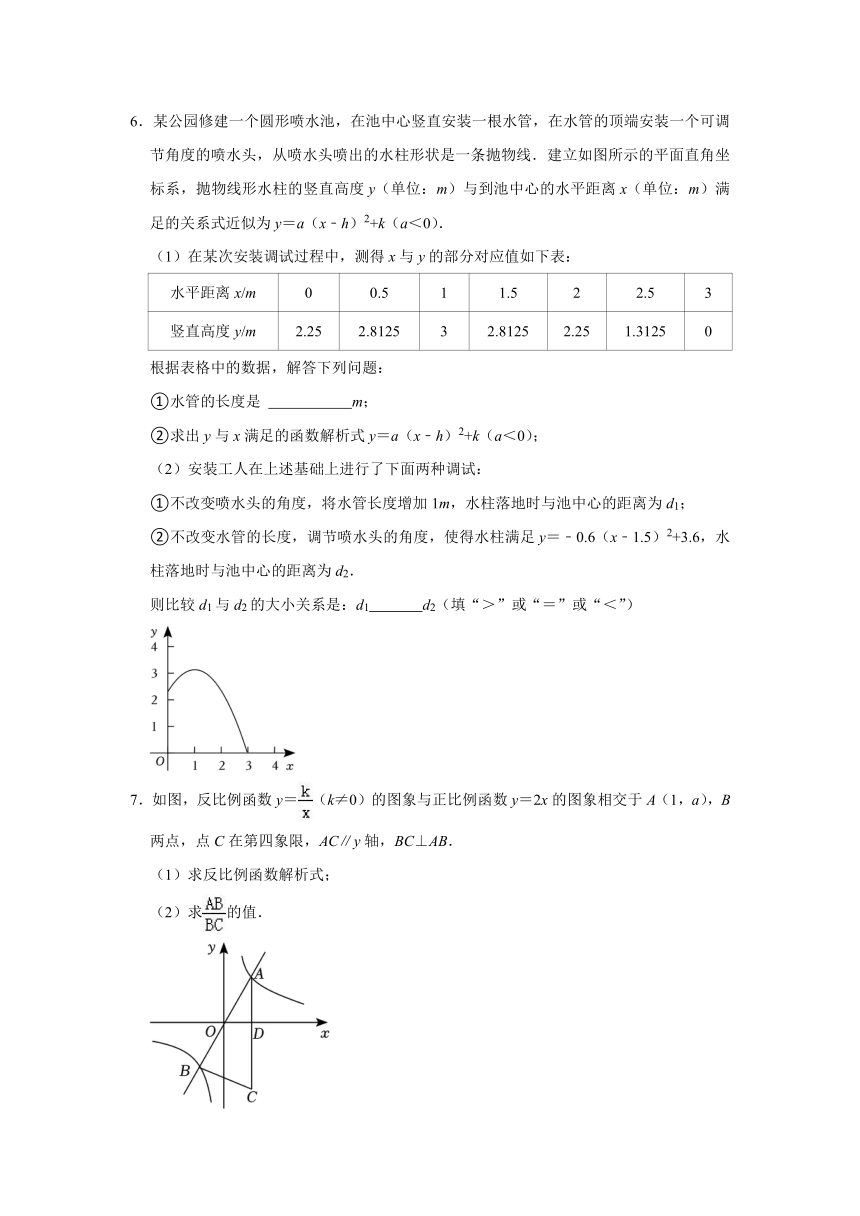
6.某公园修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安装一个可调节角度的喷水头,从喷水头喷出的水柱形状是一条抛物线.建立如图所示的平面直角坐标系,抛物线形水柱的竖直高度y(单位:m)与到池中心的水平距离x(单位:m)满足的关系式近似为y=a(x﹣h)2+k(a<0).
(1)在某次安装调试过程中,测得x与y的部分对应值如下表:
水平距离x/m 0 0.5 1 1.5 2 2.5 3
竖直高度y/m 2.25 2.8125 3 2.8125 2.25 1.3125 0
根据表格中的数据,解答下列问题:
①水管的长度是 m;
②求出y与x满足的函数解析式y=a(x﹣h)2+k(a<0);
(2)安装工人在上述基础上进行了下面两种调试:
①不改变喷水头的角度,将水管长度增加1m,水柱落地时与池中心的距离为d1;
②不改变水管的长度,调节喷水头的角度,使得水柱满足y=﹣0.6(x﹣1.5)2+3.6,水柱落地时与池中心的距离为d2.
则比较d1与d2的大小关系是:d1 d2(填“>”或“=”或“<”)
7.如图,反比例函数y=(k≠0)的图象与正比例函数y=2x的图象相交于A(1,a),B两点,点C在第四象限,AC∥y轴,BC⊥AB.
(1)求反比例函数解析式;
(2)求的值.
8.在同一平面直角坐标系中,一次函数y=kx+1和反比例函数y=的图象如图所示.
(1)求一次函数的解析式;
(2)当x>0时,直接写出不等式kx+1>的解集.
9.农户销售某农产品,经市场调查发现:若售价为6元/千克,日销售量为40千克,若售价每提高1元/千克,日销售量就减少2千克.现设售价为x元/千克(x≥6且为正整数).
(1)若某日销售量为24千克,求该日产品的单价;
(2)若政府将销售价格定为不超过18元/千克.设每日销售额为w元,求w关于x的函数表达式,并求w的最大值和最小值;
(3)市政府每日给农户补贴a元后(a为正整数),发现最大日收入(日收入=销售额+政府补贴)还是不超过450元,并且只有5种不同的单价使日收入不少于440元,请直接写出所有符合题意的a的值.
10.如图,抛物线y=ax2+bx+c经过原点,且对称轴是直线,点A(1,4)在抛物线上,点C(0,2)在y轴上,直线AC交抛物线于点A、D,点B在抛物线上,且AB∥x轴.
(1)求抛物线的解析式和点D坐标;
(2)求∠BOD的度数;
(3)设点F是线段BD的中点,点P是线段OB上一动点,将△DFP 沿FP折叠,得到△D′FP,若△D′FP与△BDP重叠部分的面积是△BDP面积的,求PB的长.
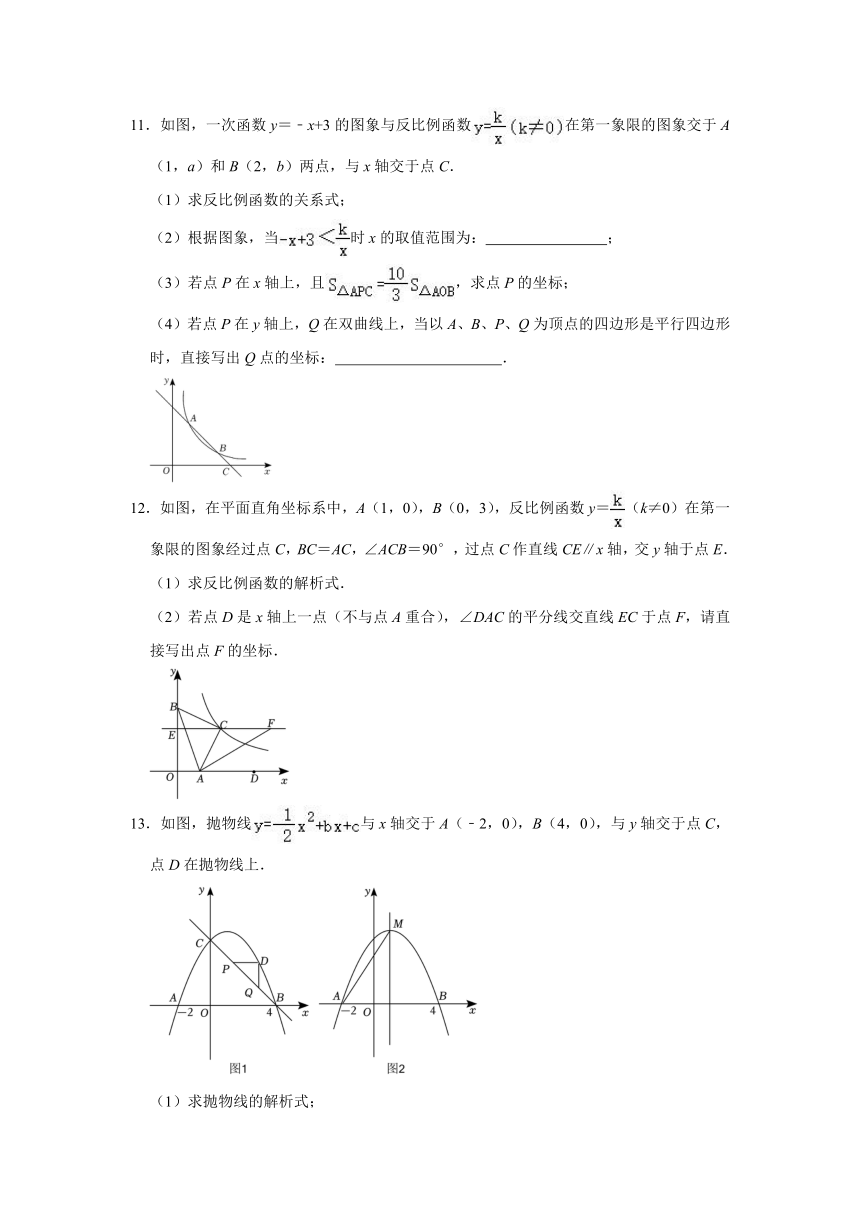
11.如图,一次函数y=﹣x+3的图象与反比例函数在第一象限的图象交于A(1,a)和B(2,b)两点,与x轴交于点C.
(1)求反比例函数的关系式;
(2)根据图象,当时x的取值范围为: ;
(3)若点P在x轴上,且,求点P的坐标;
(4)若点P在y轴上,Q在双曲线上,当以A、B、P、Q为顶点的四边形是平行四边形时,直接写出Q点的坐标: .
12.如图,在平面直角坐标系中,A(1,0),B(0,3),反比例函数y=(k≠0)在第一象限的图象经过点C,BC=AC,∠ACB=90°,过点C作直线CE∥x轴,交y轴于点E.
(1)求反比例函数的解析式.
(2)若点D是x轴上一点(不与点A重合),∠DAC的平分线交直线EC于点F,请直接写出点F的坐标.
13.如图,抛物线与x轴交于A(﹣2,0),B(4,0),与y轴交于点C,点D在抛物线上.
(1)求抛物线的解析式;
(2)如图1,连接BC,若点D为直线BC上方抛物线上的点,过点D作DP∥x轴交BC于点P,作DQ∥y轴交BC于点Q,若△DPQ的面积为2,求D点坐标;
(3)如图2,点M为抛物线的顶点,当x>﹣2时,在抛物线上是否存在点D使△AMD是等腰三角形?若能,请直接写出点D的坐标;若不能,请说明理由.
14.【阅读理解】对于任意正实数a、b,∵,∴,∴,(只有当a=b时,).
【获得结论】在(a、b均为正实数)中,若ab为定值p,则,只有当a=b时,a+b有最小值.
【探索应用】根据上述内容,回答下列问题:
(1)若m>0,只有当m= 时,有最小值 ;
(2)已知点Q(﹣4,﹣5)是双曲线上点,过Q作QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.
15.某果园有100棵橙子树,平均每棵树结600个橙子.现准备多种一些橙子树以提高果园产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子.
(1)假设果园增种x棵橙子树,那么果园共有 棵橙子树;这时平均每棵树结 个橙子.
(2)在(1)的条件下,求增种多少棵橙子树,可以使果园橙子总产量最大?最大产量是多少?
16.如图,一次函数y=k1x+b的图象与反比例函数y=的图象相交于A、B两点,其中点A的坐标为(﹣1,4),点B的坐标为(4,n).
(1)求反比例函数和一次函数的表达式.
(2)根据图象,直接写出满足k1x+b>的x的取值范围.
(3)若点P在y轴上,使得S△ABP=15,请直接写出点P的坐标.
17.已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与轴交于C点,点P是抛物线上在第一象限内的一个动点,且点P的横坐标为t.
(1)求抛物线的表达式;
(2)如图1,连接BC,PB,PC,设△PBC的面积为S.
①求S关于t的函数表达式;
②求P点到直线BC的距离的最大值,并求出此时点P的坐标.
(3)如图2,设抛物线的对称轴为l,l与x轴的交点为D,在直线l上是否存在点M,使得四边形CDPM是平行四边形?若存在,直接写出点M的坐标;若不存在,请说明理由.
18.要修建一个圆形喷水池,在池中心竖直安装一根水管,水管的顶端安一个喷水头,喷水头距池底的高度为1.88m,喷出的水柱是一条抛物线,距池中心的水平距离是1m时,水柱的高度是3.18m;距池中心的水平距离是2m时,水柱的高度是3.48m.
(1)水柱达到最高点时与池中心的水平距离是多少?
(2)水柱距地面1.5m处与池中心的水平距离是多少?
(3)为了使水柱落地点与池中心的距离是4.3m,如果只调整水管的高度,其他条件不变,出水口应升高或降低多少米?
19.如图,是8个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作Tm(m为1 8的整数).函数的图象为曲线L.
(1)若L过点T1,则k= ;
(2)若L过点T4,则它必定还过另一点Tm,则m= ;
(3)若曲线L使得T1 T8这些点分布在它的两侧,每侧各4个点,则k的整数值有 个.
20.2022年11月,“中国传统制茶技艺及其相关习俗”申遗成功,弘扬茶文化,倡导“和美雅静”的生活方式已成时尚.某茶商经销某品牌茶,成本为50元/千克,经市场调查发现,每周的销量y(千克)与销售单价x(元/千克)满足一次函数关系,部分数据列表如下:
销售单价x(元/千克) 56 65 75 …
销量y(千克) 128 110 90 …
(1)求y与x的一次函数关系式;
(2)求该茶商这一周销售该品牌茶叶所获利润w(元)的最大值.
参考答案
1.解:(1)∵点A(﹣1,﹣2)在反比例函数图象上,
∴k=2,反比例函数解析式为:y=;
∵B(2.m)在反比例函数图象上,
∴m=1,即B(2,1),
∵点AB在一次函数y1=k1x+b的图象上,
∴,解得:,
一次函数解析式为:y=x﹣1,
(2)设直线AB交x轴于点M,当y=0,x=1,M(1,0),OM=1.
所以S△AOB=S△BMO+S△AMO=+=.
2.解:(1)由抛物线的表达式知,其和x轴的交点坐标为:(﹣m,0)、(m+2,0),
则抛物线的对称轴为x=(m+2﹣m)=1;
(2)将点(0,﹣8)代入抛物线表达式得:﹣8=m(m﹣2),
解得:m=2或﹣4;
(3)由(2)知,点A、B的坐标分别为:(﹣2,0)、(4,0),
则抛物线的表达式为:y=(x+2)(x﹣4)=x2﹣2x﹣8,
当x=1时,y=x2﹣2x﹣8=﹣9,即点C(1,﹣9),
设点BC的中点为E(,﹣),
由点A、E的坐标得,直线AE的表达式为:y=﹣x﹣2,
∵D恰好是△ABC的重心,则点D为抛物线对称轴和直线AE的交点,
当x=1时,y=﹣x﹣2=﹣3,
即点D(1,﹣3),
则抛物线C2的表达式为:y=(x﹣1)2﹣3=x2﹣2x﹣2.
3.解:(1)设点D的坐标为(m,),
∵点D是OA的中点,
∴点A的坐标为(2m,),即OB=2m,AB=.
∵△OAB的面积为6,
∴×2m×=6,
∴k=3;
(2)由(1)可知,双曲线的解析式为:,
∵点C是AB和双曲线的交点,
∴点C的纵坐标为,
∴AC==,
由AC=OB,得:,
解得:或(舍去),
∴点A的坐标为(3,4).
4.解:(1)在表格取点(30,40)、(32,36),
设一次函数的表达式为:y=kx+b,
则,解得:,
则一次函数的表达式为:y=﹣2x+100;
(2)①设三月的成本为m万元,
当x=35时,y=﹣2x+100=30,
由题意得:450=30(35﹣m),
解得:m=20,
即三月份每件产品的成本是20万元;
②四月份每件产品的成本比三月份下降了14万元,则此时的成本为20﹣14=6,
由题意得:w=y(x﹣6)=(﹣2x+100)(x﹣6)=﹣2x2+112x﹣600(25≤x≤30),
则抛物线的对称轴为x=28,
则x=25时,w取得最小值,
此时,w=950,
即四月份最少利润是950万元.
5.解:(1)在正方形ABCD中,AB=BC=4,
∴A(2,4),
∵A(2,4)在y=的图象上,
∴k=2×4=8,
∵OC=OB+BC=6,
∴xE=6,
将xE=6代入y=中,得:yE=,
∴点E的坐标为(6,);
(2)设A(a,2a)(a>0),则点E(2a,),
∵S△ABO=S△CEO=×8=4,
∴S△AHO=S梯形BCEH,
∵S梯形ABCE=S△AEH+S梯形BCEH,
S△AEH+S△AHO=S△AOE=24,
∴(2a+)×2a=24,
解得a2=9,
∴k=2a2=18;
(3)答:不存在,
理由:∵AE⊥OA,
∴∠OAB+∠BAE=90°,
∵∠BAD=∠BAE+∠DAE=90°,
∴∠OAB=∠DAE,
∵∠ABO=∠D=90°,AB=AD,
∴△OAB≌△EAD(ASA),
∴OB=DE,
由①可知,A(a,2a)(a>0),则点E(2a,),
∴OB=a,ED=2a﹣=,
∴a=0,
∴k=0,
∵k>0,
∴不符合题意,不存在.
6.解:(1)①当x=0时,y=2.25,
∴水管的长度是2.25m;
故答案为:2.25;
②把x=0,y=2.25;x=1,y=3;x=3,y=0,分别代入 y=a(x﹣h)2+k,得:
,
解得:,
∴y=﹣0.75(x﹣1)2+3;
(2)①∵不改变喷水头的角度,将水管长度增加1m,
∴y=﹣0.75(x﹣1)2+3 向上平移1个单位,
∴平移后的解析式为y=﹣0.75(x﹣1)2+3+1,即 y=﹣0.75(x﹣1)2+4,
当y=0时,﹣0.75(x﹣1)2+4=0,
解得x1=+1,x2=﹣+1(不合题意,舍去),
∴d1=+1≈3.31;
对于y=﹣0.6(x﹣1.5)2+3.6,
当y=0时,﹣0.6(x﹣1.5)2+3.6=0,
解得:x1=+1.5,x2=﹣+1.5(不合题意,舍去),
∴d2=+1.5≈3.95,
∴d1<d2,
故答案为:<.
7.解:(1)∵点A(1,a)在y=2x上,
∴a=2,
∴A(1,2),
把A(1,2)代入反比例函数表达式得:k=2×1=2,
∴反比例函数的解析式为:y=;
(2)∵A、B两点关于原点成中心对称,
∴B(﹣1,﹣2);
如图所示,作BH⊥AC于H,设AC交x轴于点D,
∵∠ABC=90°,∠BHC=90°
∴∠C=∠ABH
∵CA∥y轴,BH∥x轴
∴∠AOD=∠ABH=∠C,
∴=2.
8.解:(1)由图象知,
一次函数与反比例函数的一个交点的横坐标为1,且反比例函数表达式为,
则交点的纵坐标为2.
将(1,2)代入y=kx+1得,k=1.
所以一次函数的解析式为:y=x+1.
(2)当x>0,即图象在y轴的右侧,
观察图象发现:当图象在直线x=1的右侧时,一次函数的图象在反比例函数图象的上方,
所以不等式kx+1>的解集为:x>1.
9.解(1)售价为x元/千克(x≥6且为正整数),则提价(x﹣6)元,
故销售量为[40﹣2(x﹣6)]=(52﹣2x)千克,
根据题意,得52﹣2x=24,
解得x=14,
故该日产品的单价为14元/千克.
(2)设售价为x元/千克(x≥6且为正整数),销售额为w元,则提价(x﹣6)元,
故销售量为[40﹣2(x﹣6)]=(52﹣2x)千克,
∴w=x(52﹣2x)=﹣2x2+52x,
∴w=﹣2(x﹣13)2+338,
∵6≤x≤18,且对称轴右侧,y随x的增大而减小,到对称轴距离越大,函数值越小,且13﹣6=7,18﹣13=5,
∴x=13时,w取得最大值,且最大值为338元,
∴x=6时,w取得最小值,且最小值为240元,
w=﹣2x2+52x,w的最大338元,w的最小240元.
(3)由题意得:440≤﹣2x2+52x+a≤450,由二次函数的对称性可知x的取值为11,12,13,14,15,
∴x=13时,w=338元
∴x=11或15时,w=330元,
∴x=12或14时,w=336元,
且:440≤﹣2x2+52x+a≤450,
∴110≤a≤112,
∵a是正整数,
∴a的值为110或111或112.
10.解:(1)∵抛物线经过原点,
∴c=0,
∵对称轴是直线,
∴﹣=﹣,
∴b=3a,
∴y=ax2+3ax,
将点A(1,4)代入y=ax2+3ax,
∴a+3a=4,
解得a=1,
∴抛物线的解析式为y=x2+3x,
设直线AC的解析式为y=kx+2,
∴k+2=4,
解得k=2,
∴直线AC的解析式为y=2x+2,
当2x+2=x2+3x时,解得x=﹣2或x=1,
∴D(﹣2,﹣2);
(2)∵AB∥x轴,
∴B(﹣4,4),
∴BO=4,BD=2,DO=2,
∴BD2=BO2+DO2,
∴△BDO是直角三角形,
∴∠BOD=90°;
(3)当D'在BO上方时,设FD'与BO交于点H,
∵F是BD的中点,
∴S△BPF=S△PDF,
∵S△HPF=S△BDP,
∴S△HPF=S△BFP,
∴S△HPF=S△BFH,
∴H是BP的中点,
由折叠可知,△PD'F≌△PDF,
∴S△PFD'=S△PFD,
∴S△PFH=S△PHD',
∴H是FD'的中点,
∴四边形BFPD'是平行四边形,
∴BF=D'P=PD=DF=BD=,
设P(t,﹣t),
∴=,
解得t=﹣1或t=1(舍),
∴P(﹣1,1),
∴PB=3;
当D'在BO下方时,同理可得四边形BPFD'是平行四边形,
∴BP=D'F=DF=BD=;
综上所述:PB的长为3或.
11.解:(1)把点A(1,a)代入y=﹣x+3,得a=2,
∴A(1,2),
把A(1,2)代入反比例函数,
∴k=1×2=2;
∴反比例函数的表达式为;
(2)把B(2,b)代入,得b=1,
∴B(2,1)
由(1)知A(1,2),B(2,1),
根据图象可知,当时,0<x<1或x>2,
∴当时,x的取值范围为0<x<1或x>2;
(3)解:连接OA,OB,设直线AB与x轴交于点C,如图,
∵,
又∵,
∴
设P(t,0),则OC=|t﹣3|,
∴
解得:t=8或t=﹣2,
∴P(8,0)或(﹣2,0).
(4)解:设,
当 APQB时,如图,
∵ APQB,
∴AP∥QB,PQ=AB,
∵A(1,2),B(2,1),
∴,
∴PQ2=x2+1,AB2=(1﹣2)2+(2﹣1)2=2,
∴x2+1=2,
解得:x1=1,x2=﹣1(不符合题意,舍去)
∴P(1,2),此时与点A重合,不是平行四边形,故舍去;
当 APBQ时,连接PQ交AB于D,如图,
∵ APBQ
∴点D是AB与PQ的中点,
∴
解得:x=3,
∴,
当 AQPB时,过Q作QN⊥y于N,过点B作BD⊥y于D,过点A作AS⊥BD于S,如图,
∵ AQPB
∴PQ=AB,PQ∥AB
∴∠QPN=∠BMD
∵BD⊥y
∴∠BMD+∠ABS=90°,
∵QN⊥y
∴∠PNQ=90°
∴∠PQN+∠QPN=90°
∴∠PQN=∠ABS
∵∠PNQ=∠ASB=90°
∴△PQN≌△ABS
∴PN=AS=2﹣1=1
∴PQ2=x2+1,
∵AB2=2
∴x2+1=2
解得:x1=﹣1,x2=1(不符合题意,舍去)
∴Q(﹣1,﹣2)
综上,当以A、B、P、Q为顶点的四边形是平行四边形时,Q点的坐标为或(﹣1,﹣2).
12.解:(1)过C点作MN⊥x轴于M点,过B作BN⊥CM于N点,如图所示:
∴∠AMC=∠BNC=90°,
设C(m,),
∵B(0,3),A(1,0)
则CM=,M(m,0),N(m,3),
∵AN=m﹣1,CN=3﹣,BN=m,
∵∠ACB=90°,
∴∠BCN+∠ACM=90°,
∵∠ACM+∠MAC=90°,
∴∠BCN=∠MAC,
又∵AC=BC,
∠BCN=∠MAC,
∠AMC=∠BNC=90°
∴△ACM≌△CBN(AAS),
∴CN=AM,BN=CM,
∴3﹣=m﹣1,m=,
∴k=m2,
∴3﹣m=m﹣1,
m=2,
∴k=4,
∴反比例函数的解析式:y=;
(2)由(1)可得C(2,2),
∵A(1,0),
∴AC==,
∵CE∥x轴,∠DAC的平分线交直线EC于点F,
∴F点纵坐标为2,∠CAF=DAF=∠CFA,
∴CF=AC=,
∴F点横坐标为2+,
∴F(2+,2).
13.解:(1)把A(﹣2,0),B(4,0)抛物线得:
,
解得:,
∴该抛物线的解析式为;
(2)∵点D为直线BC上方抛物线上的点,过点D作DP∥x轴交BC于点P,作DQ∥y轴交BC于点Q,△DPQ的面积为2,
把x=0代入,得:y=4,
∴C(0,4),
∵∠COB=90°,
∴∠OCB=∠OBC=45°
∵DP∥x轴,作DQ∥y轴,
∴∠DQP=45°,∠DPQ=45°,
∴∠DQP=∠DPQ=45°,
∴DP=DQ,∠PDQ=90°,
∴,
∴DQ=2,
设直线BC的解析式为y=kx+b,设直线BC的解析式为y=kx+b,把B(4,0),C(0,4)代入得:
,
解得,
∴直线BC的解析式为:y=﹣x+4,
设点,则Q(m,﹣m+4),
∴,
解得:m1=m2=2,
∴,
∴D(2,4);
(3)解:当x>﹣2时,在抛物线上存在点D使△AMD是等腰三角形,点D的坐标为:D1(4,0),,.理由如下:
∵=,
∴,
①当MA=MD时,则D与B点重合,则D1(4,0),
②当DA=DM时,如图所示,连接AM,作AM的垂直平分线交x轴于点F,AM的中点为G,
∵A(﹣2,0),,
∴,
∴,,
设x=1与x轴交于点H,则AH=3,
则,
∴,
∴,
设直线GF的解析式为y=kx+b,
∴,
解得:,
∴直线GF的解析式为,
联立,
解得:或,
∴,,
综上所述,D1(4,0),,.
14.解:(1)根据题意得当时,m=2,此时.
故答案为:2,4;
(2)连接PQ,
∵点Q(﹣4,﹣5)是双曲线上的点,
∴k=﹣4×(﹣5)=20,即,
设,
∴
=.
∴四边形AQBP的面积最小值为40.
15.解:(1)由题意得,假设果园增种x棵橙子树,那么果园共有(100+x)棵橙子树,
∴这时平均每棵树结(600﹣5x)个橙子,
故答案为:(100+x),(600﹣5x);
(2)设增种m棵橙子树时果园橙子的总产量为y个,
根据题意,得y=(100+m)(600﹣5m)=﹣5m2+100m+60000=﹣5(m﹣10)2+60500,
∵a=﹣5<0,
∴抛物线开口向下,y有最大值.
∴当m=10时,y有最大值是60500.
答:增种10棵橙子树,可以使果园橙子总产量最大,最大产量是60500个.
16.解:(1)把点A(﹣1,4)代入反比例函数y=得,4=,
∴k2=﹣4,
∴反比例函数的解析式为y=﹣,
将点B(4,n)代入y=﹣得,n=﹣=﹣1,
∴B(4,﹣1),
将A、B的坐标代入y=k1x+b得,
解得,
∴一次函数的解析式为y=﹣x+3;
(2)由图象可知:k1x+b>的x的取值范围是0<x<4或x<﹣1.
(3)在y=﹣x+3中,令x=0,则y=3,
∴直线AB与y轴的交点C为(0,3),
设P(0,n),
∴PC=|n﹣3|,
∵S△ABP=15,
∴S△ABP=S△APC+S△BPC=|n﹣3|×(4+1)=15,
∴|n﹣3|=6,
∴n=9或n=﹣3,
∴P(0,9)或(0,﹣3).
17.解:(1)(1)将A(﹣1,0),B(3,0)代入y=﹣x2+bx+c,
得,
解得:,
∴抛物线的表达式为y=﹣x2+2x+3;
(2)①在图1中,过点P作PF∥y轴,交BC于点F.
设直线BC的解析式为y=mx+n(m≠0),
将B(3,0)、C(0,3)代入y=mx+n,
,
解得:,
∴直线BC的解析式为y=﹣x+3.
∵点P的坐标为(t,﹣t2+2t+3),
∴点F的坐标为(t,﹣t+3),
∴PF=﹣t2+2t+3﹣(﹣t+3)=﹣t2+3t,
∴S=PF OB=;
②S=PF OB=,
∵<0,
∴当t=时,S取最大值,最大值为.
∵B(3,0)、C(0,3),
∴线段BC==,
∴点P到直线BC的距离的最大值为,
当时,,则此时点P的坐标为;
(3)在直线l上存在点M,使得四边形CDPM是平行四边形,理由如下:
如图2,连接PC,交抛物线对称轴l于点E,
∵抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,
∴抛物线的对称轴为直线x=1,
∵xD﹣xC=1,
∴xP﹣xM=1,
∴xP=2,
∴P(2,3),
在y=﹣x2+2x+3中,当x=0时,y=3,
∴C(0,3),
∴yC﹣yD=3,
∴yM﹣yP=3,
∴yM=6,
∴点M的坐标为(1,6);
当xP≠2时,不存在,理由如下,
若四边形CDPM是平行四边形,则CE=PE,
∵点C的横坐标为0,点E的横坐标为1,
∴点P的横坐标t=1×2﹣0=2,
又∵xP≠2,
∴不存在,
综上所述,在直线l上存在点M,使得四边形CDPM是平行四边形,点M的坐标为M(1,6).
18.解:(1)如图,建立以池中心为原点,竖直安装的水管为y轴,与水管垂直的为x轴建立直角坐标系,
设抛物线解析式为y=ax2+bx+c,
把(0,1.88),(1,3.18),(2,3.48)代入解析式得:
,
解得,
∴y=﹣0.5x2+1.8x+1.88=﹣0.5(x﹣1.8)2+3.5,
∴当x=1.8时,y有最大值为3.5,
∴水柱达到最高点时与池中心的水平距离是1.8米;
(2)当y=1.5时,则﹣0.5(x﹣1.8)2+3.5=1.5,
解得x1=3.8,x2=﹣0.2(舍去),
∴x=3.8,
∴水柱距地面1.5m处与池中心的水平距离是3.8m;
(3)根据题意,设y=﹣0.5(x﹣1.8)2+3.5+m,
把(4.3,0)代入,得﹣0.5(4.3﹣1.8)2+3.5+m=0,
解得m=0.375,
∴出水口应升高0.375m.
19.解:(1)由图象可知T1(﹣16,1)
又∵函数y=(x<0)的图象经过T1,
∴1=,即k=﹣16,
故答案为:﹣16;
(2)由图象可知T1(﹣16,1)、T2(﹣14,2)、T3(﹣12,3)、T4(﹣10,4)、T5(﹣8,5)、T6(﹣6,6)、T7(﹣4,7)、T8(﹣2,8),
∵L过点T4,
∴k=﹣10×4=40,
观察T1~T8发现T5符合题意,即m=5,
故答案为:5;
(3)∵T1~T8横纵坐标积分别为:﹣16,﹣28,﹣36,﹣40,﹣40,﹣36,﹣28,﹣16,
∴要使这8个点为于L的两侧,每次各四个点,k必须满足﹣36<k<﹣28,
∴k可取共7个整数值,为﹣35、﹣34、﹣33、﹣32、﹣31、﹣30、﹣29.
故答案为:7.
20.解:(1)设y与x的一次函数关系式为y=kx+b(k≠0),
由题意得:,
解得:,
则y与x的一次函数关系式为y=﹣2x+240.
(2)由题意得:w=(x﹣50)y=(x﹣50)(﹣2x+240)
=﹣2x2+340x﹣12000
=﹣2(x﹣85)2+2450,
∵这个抛物线的对称轴为直线x=85,且开口向下,
∴当x=85时,w取得最大值,最大值为2450,
答:该茶商这一周销售该品牌茶叶所获利润w(元)的最大值为2450元.
解答题专题训练(附答案)
1.如图,已知一次函数y1=k1x+b的图象与反比例函数y2=,分别交于点A和点B,且A、B两点的坐标分别是A(﹣1,﹣2)和B(2.m),连接OA、OB.
(1)求一次函数y1=k1x+b与反比例函数y2=的函数表达式;
(2)求△AOB的面积.
2.如图,在平面直角坐标系中,抛物线C1:y=(x+m)(x﹣m﹣2)与x轴交于点A和点B,顶点为C.
(1)求抛物线C1的对称轴;
(2)若抛物线C1经过点(0,﹣8),求m的值;
(3)在(2)的条件下,将抛物线C1向上平移至抛物线C2,此时抛物线C2的顶点D恰好是△ABC的重心,求抛物线C2的函数表达式.
3.如图,Rt△OAB的直角顶点B在x轴的正半轴上,点A在第一象限内,已知反比例函数(x>0)的图象经过线段OA的中点D,交直线AB于点C.若△OAB的面积为6.
(1)求k的值;
(2)若AC=OB,求点A的坐标.
4.某工厂生产一种产品,经市场调查发现,该产品每月的销售量y(件)与售价x(万元/件)之间满足一次函数关系,部分数据如表:
每件售价x/万元 … 24 26 28 30 32 …
月销售量y/件 … 52 48 44 40 36 …
(1)求y与x的函数关系式(不写自变量的取值范围).
(2)该产品今年三月份的售价为35万元/件,利润为450万元.
①求:三月份每件产品的成本是多少万元?
②四月份工厂为了降低成本,提高产品质量,投资了450万元改进设备和革新技术,使每件产品的成本比三月份下降了14万元.若四月份每件产品的售价至少为25万元,且不高于30万元,求这个月获得的利润w(万元)关于售价x(万元/件)的函数关系式,并求最少利润是多少万元.
5.如图,直线y=2x与双曲线y=(x>0,k>0)相交于点A,AB⊥x轴于点B,以AB为边在右侧作正方形ABCD,CD与双曲线相交于点E,连接AE、OE.
(1)当BC=4时,求点E的坐标;
(2)当S△AOE=24时,求k的值;
(3)是否存在实数k,满足AE⊥OA,若存在,求出k的值;若不存在,请说明理由.
6.某公园修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安装一个可调节角度的喷水头,从喷水头喷出的水柱形状是一条抛物线.建立如图所示的平面直角坐标系,抛物线形水柱的竖直高度y(单位:m)与到池中心的水平距离x(单位:m)满足的关系式近似为y=a(x﹣h)2+k(a<0).
(1)在某次安装调试过程中,测得x与y的部分对应值如下表:
水平距离x/m 0 0.5 1 1.5 2 2.5 3
竖直高度y/m 2.25 2.8125 3 2.8125 2.25 1.3125 0
根据表格中的数据,解答下列问题:
①水管的长度是 m;
②求出y与x满足的函数解析式y=a(x﹣h)2+k(a<0);
(2)安装工人在上述基础上进行了下面两种调试:
①不改变喷水头的角度,将水管长度增加1m,水柱落地时与池中心的距离为d1;
②不改变水管的长度,调节喷水头的角度,使得水柱满足y=﹣0.6(x﹣1.5)2+3.6,水柱落地时与池中心的距离为d2.
则比较d1与d2的大小关系是:d1 d2(填“>”或“=”或“<”)
7.如图,反比例函数y=(k≠0)的图象与正比例函数y=2x的图象相交于A(1,a),B两点,点C在第四象限,AC∥y轴,BC⊥AB.
(1)求反比例函数解析式;
(2)求的值.
8.在同一平面直角坐标系中,一次函数y=kx+1和反比例函数y=的图象如图所示.
(1)求一次函数的解析式;
(2)当x>0时,直接写出不等式kx+1>的解集.
9.农户销售某农产品,经市场调查发现:若售价为6元/千克,日销售量为40千克,若售价每提高1元/千克,日销售量就减少2千克.现设售价为x元/千克(x≥6且为正整数).
(1)若某日销售量为24千克,求该日产品的单价;
(2)若政府将销售价格定为不超过18元/千克.设每日销售额为w元,求w关于x的函数表达式,并求w的最大值和最小值;
(3)市政府每日给农户补贴a元后(a为正整数),发现最大日收入(日收入=销售额+政府补贴)还是不超过450元,并且只有5种不同的单价使日收入不少于440元,请直接写出所有符合题意的a的值.
10.如图,抛物线y=ax2+bx+c经过原点,且对称轴是直线,点A(1,4)在抛物线上,点C(0,2)在y轴上,直线AC交抛物线于点A、D,点B在抛物线上,且AB∥x轴.
(1)求抛物线的解析式和点D坐标;
(2)求∠BOD的度数;
(3)设点F是线段BD的中点,点P是线段OB上一动点,将△DFP 沿FP折叠,得到△D′FP,若△D′FP与△BDP重叠部分的面积是△BDP面积的,求PB的长.
11.如图,一次函数y=﹣x+3的图象与反比例函数在第一象限的图象交于A(1,a)和B(2,b)两点,与x轴交于点C.
(1)求反比例函数的关系式;
(2)根据图象,当时x的取值范围为: ;
(3)若点P在x轴上,且,求点P的坐标;
(4)若点P在y轴上,Q在双曲线上,当以A、B、P、Q为顶点的四边形是平行四边形时,直接写出Q点的坐标: .
12.如图,在平面直角坐标系中,A(1,0),B(0,3),反比例函数y=(k≠0)在第一象限的图象经过点C,BC=AC,∠ACB=90°,过点C作直线CE∥x轴,交y轴于点E.
(1)求反比例函数的解析式.
(2)若点D是x轴上一点(不与点A重合),∠DAC的平分线交直线EC于点F,请直接写出点F的坐标.
13.如图,抛物线与x轴交于A(﹣2,0),B(4,0),与y轴交于点C,点D在抛物线上.
(1)求抛物线的解析式;
(2)如图1,连接BC,若点D为直线BC上方抛物线上的点,过点D作DP∥x轴交BC于点P,作DQ∥y轴交BC于点Q,若△DPQ的面积为2,求D点坐标;
(3)如图2,点M为抛物线的顶点,当x>﹣2时,在抛物线上是否存在点D使△AMD是等腰三角形?若能,请直接写出点D的坐标;若不能,请说明理由.
14.【阅读理解】对于任意正实数a、b,∵,∴,∴,(只有当a=b时,).
【获得结论】在(a、b均为正实数)中,若ab为定值p,则,只有当a=b时,a+b有最小值.
【探索应用】根据上述内容,回答下列问题:
(1)若m>0,只有当m= 时,有最小值 ;
(2)已知点Q(﹣4,﹣5)是双曲线上点,过Q作QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.
15.某果园有100棵橙子树,平均每棵树结600个橙子.现准备多种一些橙子树以提高果园产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子.
(1)假设果园增种x棵橙子树,那么果园共有 棵橙子树;这时平均每棵树结 个橙子.
(2)在(1)的条件下,求增种多少棵橙子树,可以使果园橙子总产量最大?最大产量是多少?
16.如图,一次函数y=k1x+b的图象与反比例函数y=的图象相交于A、B两点,其中点A的坐标为(﹣1,4),点B的坐标为(4,n).
(1)求反比例函数和一次函数的表达式.
(2)根据图象,直接写出满足k1x+b>的x的取值范围.
(3)若点P在y轴上,使得S△ABP=15,请直接写出点P的坐标.
17.已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与轴交于C点,点P是抛物线上在第一象限内的一个动点,且点P的横坐标为t.
(1)求抛物线的表达式;
(2)如图1,连接BC,PB,PC,设△PBC的面积为S.
①求S关于t的函数表达式;
②求P点到直线BC的距离的最大值,并求出此时点P的坐标.
(3)如图2,设抛物线的对称轴为l,l与x轴的交点为D,在直线l上是否存在点M,使得四边形CDPM是平行四边形?若存在,直接写出点M的坐标;若不存在,请说明理由.
18.要修建一个圆形喷水池,在池中心竖直安装一根水管,水管的顶端安一个喷水头,喷水头距池底的高度为1.88m,喷出的水柱是一条抛物线,距池中心的水平距离是1m时,水柱的高度是3.18m;距池中心的水平距离是2m时,水柱的高度是3.48m.
(1)水柱达到最高点时与池中心的水平距离是多少?
(2)水柱距地面1.5m处与池中心的水平距离是多少?
(3)为了使水柱落地点与池中心的距离是4.3m,如果只调整水管的高度,其他条件不变,出水口应升高或降低多少米?
19.如图,是8个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作Tm(m为1 8的整数).函数的图象为曲线L.
(1)若L过点T1,则k= ;
(2)若L过点T4,则它必定还过另一点Tm,则m= ;
(3)若曲线L使得T1 T8这些点分布在它的两侧,每侧各4个点,则k的整数值有 个.
20.2022年11月,“中国传统制茶技艺及其相关习俗”申遗成功,弘扬茶文化,倡导“和美雅静”的生活方式已成时尚.某茶商经销某品牌茶,成本为50元/千克,经市场调查发现,每周的销量y(千克)与销售单价x(元/千克)满足一次函数关系,部分数据列表如下:
销售单价x(元/千克) 56 65 75 …
销量y(千克) 128 110 90 …
(1)求y与x的一次函数关系式;
(2)求该茶商这一周销售该品牌茶叶所获利润w(元)的最大值.
参考答案
1.解:(1)∵点A(﹣1,﹣2)在反比例函数图象上,
∴k=2,反比例函数解析式为:y=;
∵B(2.m)在反比例函数图象上,
∴m=1,即B(2,1),
∵点AB在一次函数y1=k1x+b的图象上,
∴,解得:,
一次函数解析式为:y=x﹣1,
(2)设直线AB交x轴于点M,当y=0,x=1,M(1,0),OM=1.
所以S△AOB=S△BMO+S△AMO=+=.
2.解:(1)由抛物线的表达式知,其和x轴的交点坐标为:(﹣m,0)、(m+2,0),
则抛物线的对称轴为x=(m+2﹣m)=1;
(2)将点(0,﹣8)代入抛物线表达式得:﹣8=m(m﹣2),
解得:m=2或﹣4;
(3)由(2)知,点A、B的坐标分别为:(﹣2,0)、(4,0),
则抛物线的表达式为:y=(x+2)(x﹣4)=x2﹣2x﹣8,
当x=1时,y=x2﹣2x﹣8=﹣9,即点C(1,﹣9),
设点BC的中点为E(,﹣),
由点A、E的坐标得,直线AE的表达式为:y=﹣x﹣2,
∵D恰好是△ABC的重心,则点D为抛物线对称轴和直线AE的交点,
当x=1时,y=﹣x﹣2=﹣3,
即点D(1,﹣3),
则抛物线C2的表达式为:y=(x﹣1)2﹣3=x2﹣2x﹣2.
3.解:(1)设点D的坐标为(m,),
∵点D是OA的中点,
∴点A的坐标为(2m,),即OB=2m,AB=.
∵△OAB的面积为6,
∴×2m×=6,
∴k=3;
(2)由(1)可知,双曲线的解析式为:,
∵点C是AB和双曲线的交点,
∴点C的纵坐标为,
∴AC==,
由AC=OB,得:,
解得:或(舍去),
∴点A的坐标为(3,4).
4.解:(1)在表格取点(30,40)、(32,36),
设一次函数的表达式为:y=kx+b,
则,解得:,
则一次函数的表达式为:y=﹣2x+100;
(2)①设三月的成本为m万元,
当x=35时,y=﹣2x+100=30,
由题意得:450=30(35﹣m),
解得:m=20,
即三月份每件产品的成本是20万元;
②四月份每件产品的成本比三月份下降了14万元,则此时的成本为20﹣14=6,
由题意得:w=y(x﹣6)=(﹣2x+100)(x﹣6)=﹣2x2+112x﹣600(25≤x≤30),
则抛物线的对称轴为x=28,
则x=25时,w取得最小值,
此时,w=950,
即四月份最少利润是950万元.
5.解:(1)在正方形ABCD中,AB=BC=4,
∴A(2,4),
∵A(2,4)在y=的图象上,
∴k=2×4=8,
∵OC=OB+BC=6,
∴xE=6,
将xE=6代入y=中,得:yE=,
∴点E的坐标为(6,);
(2)设A(a,2a)(a>0),则点E(2a,),
∵S△ABO=S△CEO=×8=4,
∴S△AHO=S梯形BCEH,
∵S梯形ABCE=S△AEH+S梯形BCEH,
S△AEH+S△AHO=S△AOE=24,
∴(2a+)×2a=24,
解得a2=9,
∴k=2a2=18;
(3)答:不存在,
理由:∵AE⊥OA,
∴∠OAB+∠BAE=90°,
∵∠BAD=∠BAE+∠DAE=90°,
∴∠OAB=∠DAE,
∵∠ABO=∠D=90°,AB=AD,
∴△OAB≌△EAD(ASA),
∴OB=DE,
由①可知,A(a,2a)(a>0),则点E(2a,),
∴OB=a,ED=2a﹣=,
∴a=0,
∴k=0,
∵k>0,
∴不符合题意,不存在.
6.解:(1)①当x=0时,y=2.25,
∴水管的长度是2.25m;
故答案为:2.25;
②把x=0,y=2.25;x=1,y=3;x=3,y=0,分别代入 y=a(x﹣h)2+k,得:
,
解得:,
∴y=﹣0.75(x﹣1)2+3;
(2)①∵不改变喷水头的角度,将水管长度增加1m,
∴y=﹣0.75(x﹣1)2+3 向上平移1个单位,
∴平移后的解析式为y=﹣0.75(x﹣1)2+3+1,即 y=﹣0.75(x﹣1)2+4,
当y=0时,﹣0.75(x﹣1)2+4=0,
解得x1=+1,x2=﹣+1(不合题意,舍去),
∴d1=+1≈3.31;
对于y=﹣0.6(x﹣1.5)2+3.6,
当y=0时,﹣0.6(x﹣1.5)2+3.6=0,
解得:x1=+1.5,x2=﹣+1.5(不合题意,舍去),
∴d2=+1.5≈3.95,
∴d1<d2,
故答案为:<.
7.解:(1)∵点A(1,a)在y=2x上,
∴a=2,
∴A(1,2),
把A(1,2)代入反比例函数表达式得:k=2×1=2,
∴反比例函数的解析式为:y=;
(2)∵A、B两点关于原点成中心对称,
∴B(﹣1,﹣2);
如图所示,作BH⊥AC于H,设AC交x轴于点D,
∵∠ABC=90°,∠BHC=90°
∴∠C=∠ABH
∵CA∥y轴,BH∥x轴
∴∠AOD=∠ABH=∠C,
∴=2.
8.解:(1)由图象知,
一次函数与反比例函数的一个交点的横坐标为1,且反比例函数表达式为,
则交点的纵坐标为2.
将(1,2)代入y=kx+1得,k=1.
所以一次函数的解析式为:y=x+1.
(2)当x>0,即图象在y轴的右侧,
观察图象发现:当图象在直线x=1的右侧时,一次函数的图象在反比例函数图象的上方,
所以不等式kx+1>的解集为:x>1.
9.解(1)售价为x元/千克(x≥6且为正整数),则提价(x﹣6)元,
故销售量为[40﹣2(x﹣6)]=(52﹣2x)千克,
根据题意,得52﹣2x=24,
解得x=14,
故该日产品的单价为14元/千克.
(2)设售价为x元/千克(x≥6且为正整数),销售额为w元,则提价(x﹣6)元,
故销售量为[40﹣2(x﹣6)]=(52﹣2x)千克,
∴w=x(52﹣2x)=﹣2x2+52x,
∴w=﹣2(x﹣13)2+338,
∵6≤x≤18,且对称轴右侧,y随x的增大而减小,到对称轴距离越大,函数值越小,且13﹣6=7,18﹣13=5,
∴x=13时,w取得最大值,且最大值为338元,
∴x=6时,w取得最小值,且最小值为240元,
w=﹣2x2+52x,w的最大338元,w的最小240元.
(3)由题意得:440≤﹣2x2+52x+a≤450,由二次函数的对称性可知x的取值为11,12,13,14,15,
∴x=13时,w=338元
∴x=11或15时,w=330元,
∴x=12或14时,w=336元,
且:440≤﹣2x2+52x+a≤450,
∴110≤a≤112,
∵a是正整数,
∴a的值为110或111或112.
10.解:(1)∵抛物线经过原点,
∴c=0,
∵对称轴是直线,
∴﹣=﹣,
∴b=3a,
∴y=ax2+3ax,
将点A(1,4)代入y=ax2+3ax,
∴a+3a=4,
解得a=1,
∴抛物线的解析式为y=x2+3x,
设直线AC的解析式为y=kx+2,
∴k+2=4,
解得k=2,
∴直线AC的解析式为y=2x+2,
当2x+2=x2+3x时,解得x=﹣2或x=1,
∴D(﹣2,﹣2);
(2)∵AB∥x轴,
∴B(﹣4,4),
∴BO=4,BD=2,DO=2,
∴BD2=BO2+DO2,
∴△BDO是直角三角形,
∴∠BOD=90°;
(3)当D'在BO上方时,设FD'与BO交于点H,
∵F是BD的中点,
∴S△BPF=S△PDF,
∵S△HPF=S△BDP,
∴S△HPF=S△BFP,
∴S△HPF=S△BFH,
∴H是BP的中点,
由折叠可知,△PD'F≌△PDF,
∴S△PFD'=S△PFD,
∴S△PFH=S△PHD',
∴H是FD'的中点,
∴四边形BFPD'是平行四边形,
∴BF=D'P=PD=DF=BD=,
设P(t,﹣t),
∴=,
解得t=﹣1或t=1(舍),
∴P(﹣1,1),
∴PB=3;
当D'在BO下方时,同理可得四边形BPFD'是平行四边形,
∴BP=D'F=DF=BD=;
综上所述:PB的长为3或.
11.解:(1)把点A(1,a)代入y=﹣x+3,得a=2,
∴A(1,2),
把A(1,2)代入反比例函数,
∴k=1×2=2;
∴反比例函数的表达式为;
(2)把B(2,b)代入,得b=1,
∴B(2,1)
由(1)知A(1,2),B(2,1),
根据图象可知,当时,0<x<1或x>2,
∴当时,x的取值范围为0<x<1或x>2;
(3)解:连接OA,OB,设直线AB与x轴交于点C,如图,
∵,
又∵,
∴
设P(t,0),则OC=|t﹣3|,
∴
解得:t=8或t=﹣2,
∴P(8,0)或(﹣2,0).
(4)解:设,
当 APQB时,如图,
∵ APQB,
∴AP∥QB,PQ=AB,
∵A(1,2),B(2,1),
∴,
∴PQ2=x2+1,AB2=(1﹣2)2+(2﹣1)2=2,
∴x2+1=2,
解得:x1=1,x2=﹣1(不符合题意,舍去)
∴P(1,2),此时与点A重合,不是平行四边形,故舍去;
当 APBQ时,连接PQ交AB于D,如图,
∵ APBQ
∴点D是AB与PQ的中点,
∴
解得:x=3,
∴,
当 AQPB时,过Q作QN⊥y于N,过点B作BD⊥y于D,过点A作AS⊥BD于S,如图,
∵ AQPB
∴PQ=AB,PQ∥AB
∴∠QPN=∠BMD
∵BD⊥y
∴∠BMD+∠ABS=90°,
∵QN⊥y
∴∠PNQ=90°
∴∠PQN+∠QPN=90°
∴∠PQN=∠ABS
∵∠PNQ=∠ASB=90°
∴△PQN≌△ABS
∴PN=AS=2﹣1=1
∴PQ2=x2+1,
∵AB2=2
∴x2+1=2
解得:x1=﹣1,x2=1(不符合题意,舍去)
∴Q(﹣1,﹣2)
综上,当以A、B、P、Q为顶点的四边形是平行四边形时,Q点的坐标为或(﹣1,﹣2).
12.解:(1)过C点作MN⊥x轴于M点,过B作BN⊥CM于N点,如图所示:
∴∠AMC=∠BNC=90°,
设C(m,),
∵B(0,3),A(1,0)
则CM=,M(m,0),N(m,3),
∵AN=m﹣1,CN=3﹣,BN=m,
∵∠ACB=90°,
∴∠BCN+∠ACM=90°,
∵∠ACM+∠MAC=90°,
∴∠BCN=∠MAC,
又∵AC=BC,
∠BCN=∠MAC,
∠AMC=∠BNC=90°
∴△ACM≌△CBN(AAS),
∴CN=AM,BN=CM,
∴3﹣=m﹣1,m=,
∴k=m2,
∴3﹣m=m﹣1,
m=2,
∴k=4,
∴反比例函数的解析式:y=;
(2)由(1)可得C(2,2),
∵A(1,0),
∴AC==,
∵CE∥x轴,∠DAC的平分线交直线EC于点F,
∴F点纵坐标为2,∠CAF=DAF=∠CFA,
∴CF=AC=,
∴F点横坐标为2+,
∴F(2+,2).
13.解:(1)把A(﹣2,0),B(4,0)抛物线得:
,
解得:,
∴该抛物线的解析式为;
(2)∵点D为直线BC上方抛物线上的点,过点D作DP∥x轴交BC于点P,作DQ∥y轴交BC于点Q,△DPQ的面积为2,
把x=0代入,得:y=4,
∴C(0,4),
∵∠COB=90°,
∴∠OCB=∠OBC=45°
∵DP∥x轴,作DQ∥y轴,
∴∠DQP=45°,∠DPQ=45°,
∴∠DQP=∠DPQ=45°,
∴DP=DQ,∠PDQ=90°,
∴,
∴DQ=2,
设直线BC的解析式为y=kx+b,设直线BC的解析式为y=kx+b,把B(4,0),C(0,4)代入得:
,
解得,
∴直线BC的解析式为:y=﹣x+4,
设点,则Q(m,﹣m+4),
∴,
解得:m1=m2=2,
∴,
∴D(2,4);
(3)解:当x>﹣2时,在抛物线上存在点D使△AMD是等腰三角形,点D的坐标为:D1(4,0),,.理由如下:
∵=,
∴,
①当MA=MD时,则D与B点重合,则D1(4,0),
②当DA=DM时,如图所示,连接AM,作AM的垂直平分线交x轴于点F,AM的中点为G,
∵A(﹣2,0),,
∴,
∴,,
设x=1与x轴交于点H,则AH=3,
则,
∴,
∴,
设直线GF的解析式为y=kx+b,
∴,
解得:,
∴直线GF的解析式为,
联立,
解得:或,
∴,,
综上所述,D1(4,0),,.
14.解:(1)根据题意得当时,m=2,此时.
故答案为:2,4;
(2)连接PQ,
∵点Q(﹣4,﹣5)是双曲线上的点,
∴k=﹣4×(﹣5)=20,即,
设,
∴
=.
∴四边形AQBP的面积最小值为40.
15.解:(1)由题意得,假设果园增种x棵橙子树,那么果园共有(100+x)棵橙子树,
∴这时平均每棵树结(600﹣5x)个橙子,
故答案为:(100+x),(600﹣5x);
(2)设增种m棵橙子树时果园橙子的总产量为y个,
根据题意,得y=(100+m)(600﹣5m)=﹣5m2+100m+60000=﹣5(m﹣10)2+60500,
∵a=﹣5<0,
∴抛物线开口向下,y有最大值.
∴当m=10时,y有最大值是60500.
答:增种10棵橙子树,可以使果园橙子总产量最大,最大产量是60500个.
16.解:(1)把点A(﹣1,4)代入反比例函数y=得,4=,
∴k2=﹣4,
∴反比例函数的解析式为y=﹣,
将点B(4,n)代入y=﹣得,n=﹣=﹣1,
∴B(4,﹣1),
将A、B的坐标代入y=k1x+b得,
解得,
∴一次函数的解析式为y=﹣x+3;
(2)由图象可知:k1x+b>的x的取值范围是0<x<4或x<﹣1.
(3)在y=﹣x+3中,令x=0,则y=3,
∴直线AB与y轴的交点C为(0,3),
设P(0,n),
∴PC=|n﹣3|,
∵S△ABP=15,
∴S△ABP=S△APC+S△BPC=|n﹣3|×(4+1)=15,
∴|n﹣3|=6,
∴n=9或n=﹣3,
∴P(0,9)或(0,﹣3).
17.解:(1)(1)将A(﹣1,0),B(3,0)代入y=﹣x2+bx+c,
得,
解得:,
∴抛物线的表达式为y=﹣x2+2x+3;
(2)①在图1中,过点P作PF∥y轴,交BC于点F.
设直线BC的解析式为y=mx+n(m≠0),
将B(3,0)、C(0,3)代入y=mx+n,
,
解得:,
∴直线BC的解析式为y=﹣x+3.
∵点P的坐标为(t,﹣t2+2t+3),
∴点F的坐标为(t,﹣t+3),
∴PF=﹣t2+2t+3﹣(﹣t+3)=﹣t2+3t,
∴S=PF OB=;
②S=PF OB=,
∵<0,
∴当t=时,S取最大值,最大值为.
∵B(3,0)、C(0,3),
∴线段BC==,
∴点P到直线BC的距离的最大值为,
当时,,则此时点P的坐标为;
(3)在直线l上存在点M,使得四边形CDPM是平行四边形,理由如下:
如图2,连接PC,交抛物线对称轴l于点E,
∵抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,
∴抛物线的对称轴为直线x=1,
∵xD﹣xC=1,
∴xP﹣xM=1,
∴xP=2,
∴P(2,3),
在y=﹣x2+2x+3中,当x=0时,y=3,
∴C(0,3),
∴yC﹣yD=3,
∴yM﹣yP=3,
∴yM=6,
∴点M的坐标为(1,6);
当xP≠2时,不存在,理由如下,
若四边形CDPM是平行四边形,则CE=PE,
∵点C的横坐标为0,点E的横坐标为1,
∴点P的横坐标t=1×2﹣0=2,
又∵xP≠2,
∴不存在,
综上所述,在直线l上存在点M,使得四边形CDPM是平行四边形,点M的坐标为M(1,6).
18.解:(1)如图,建立以池中心为原点,竖直安装的水管为y轴,与水管垂直的为x轴建立直角坐标系,
设抛物线解析式为y=ax2+bx+c,
把(0,1.88),(1,3.18),(2,3.48)代入解析式得:
,
解得,
∴y=﹣0.5x2+1.8x+1.88=﹣0.5(x﹣1.8)2+3.5,
∴当x=1.8时,y有最大值为3.5,
∴水柱达到最高点时与池中心的水平距离是1.8米;
(2)当y=1.5时,则﹣0.5(x﹣1.8)2+3.5=1.5,
解得x1=3.8,x2=﹣0.2(舍去),
∴x=3.8,
∴水柱距地面1.5m处与池中心的水平距离是3.8m;
(3)根据题意,设y=﹣0.5(x﹣1.8)2+3.5+m,
把(4.3,0)代入,得﹣0.5(4.3﹣1.8)2+3.5+m=0,
解得m=0.375,
∴出水口应升高0.375m.
19.解:(1)由图象可知T1(﹣16,1)
又∵函数y=(x<0)的图象经过T1,
∴1=,即k=﹣16,
故答案为:﹣16;
(2)由图象可知T1(﹣16,1)、T2(﹣14,2)、T3(﹣12,3)、T4(﹣10,4)、T5(﹣8,5)、T6(﹣6,6)、T7(﹣4,7)、T8(﹣2,8),
∵L过点T4,
∴k=﹣10×4=40,
观察T1~T8发现T5符合题意,即m=5,
故答案为:5;
(3)∵T1~T8横纵坐标积分别为:﹣16,﹣28,﹣36,﹣40,﹣40,﹣36,﹣28,﹣16,
∴要使这8个点为于L的两侧,每次各四个点,k必须满足﹣36<k<﹣28,
∴k可取共7个整数值,为﹣35、﹣34、﹣33、﹣32、﹣31、﹣30、﹣29.
故答案为:7.
20.解:(1)设y与x的一次函数关系式为y=kx+b(k≠0),
由题意得:,
解得:,
则y与x的一次函数关系式为y=﹣2x+240.
(2)由题意得:w=(x﹣50)y=(x﹣50)(﹣2x+240)
=﹣2x2+340x﹣12000
=﹣2(x﹣85)2+2450,
∵这个抛物线的对称轴为直线x=85,且开口向下,
∴当x=85时,w取得最大值,最大值为2450,
答:该茶商这一周销售该品牌茶叶所获利润w(元)的最大值为2450元.
