1.4.1 有理数的乘法 第1课时 有理数的乘法法则(含倒数) 课件 (共28张PPT)【2023秋人教七上数学高效实用备课】
文档属性
| 名称 | 1.4.1 有理数的乘法 第1课时 有理数的乘法法则(含倒数) 课件 (共28张PPT)【2023秋人教七上数学高效实用备课】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-19 20:29:29 | ||
图片预览








文档简介
(共28张PPT)
人教七上数学同步精品课件
人教版七年级上册
第一章 有理数
第1课时 有理数的乘法法则(含倒数)
1_4_1有理数的乘法
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1.掌握有理数的乘法法则,并能熟练地进行两个数的乘法运算.
2.会求一个数的倒数.
学习目标
重点
重点
我们已经熟悉正数及0的乘法运算.
与加法类似,引入负数后,将出现 3×(-3),(-3)×3,(-3)×(-3)这样的乘法.
该怎样进行这一类的运算呢?
新课引入
一、有理数的乘法法则
3 × 3 = 9,
3 × 2 = 6,
3 × 1 = 3,
3 × 0 = 0.
思考
随着第二个乘数逐次递减1,积逐次递减3.
观察下面的乘法算式,你能发现什么规律吗
新知学习
3×(-1)=-3,
3×(-2)=_______.
3×(-3)=_______.
-6
-9
随着第二个乘数逐次递减1,积逐次递减3.
要使这个规律在引入负数后仍然成立,那么应有:
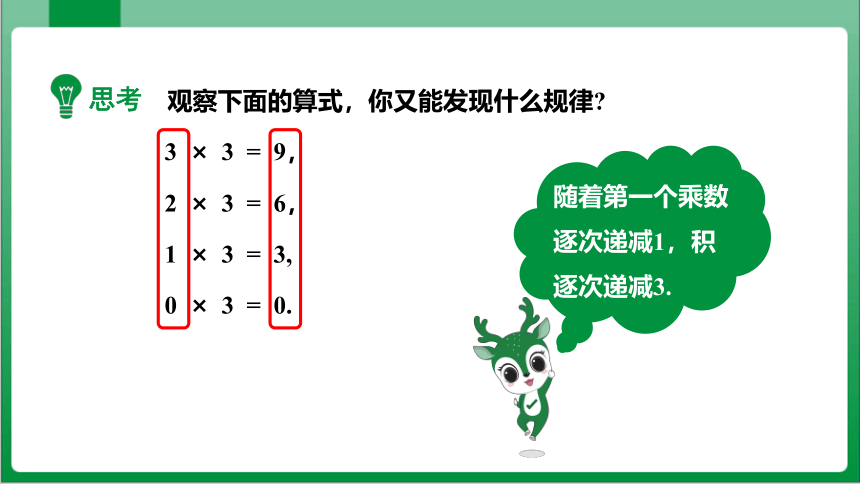
3 × 3 = 9,
2 × 3 = 6,
1 × 3 = 3,
0 × 3 = 0.
思考
随着第一个乘数逐次递减1,积逐次递减3.
观察下面的算式,你又能发现什么规律
要使这个规律在引入负数后仍然成立,那么应有:
(-1)×3=-3,
(-2)×3=_______.
(-3)×3=_______.
-6
-9
随着第一个乘数逐次递减1,积逐次递减3.
从符号和绝对值两个角度观察上述4个算式,你能发现什么规律
正数×正数 =正数
3 × 3 = 9,
3 × 2 = 6,
3 × 1 = 3,
3 × 0 = 0.
3× (-1)= -3,
3× (-2)= -6.
3× (-3)= -9.
3 × 3 = 9,
2 × 3 = 6,
1 × 3 = 3,
0 × 3 = 0.
(-1) ×3= -3,
(-2) ×3= -6.
(-3) ×3= -9.
正数×负数 =负数
正数×正数 =正数
负数×正数 =负数
积的绝对值=各乘数绝对值的积.
正数乘正数,积为正数;
正数乘负数,积为负数;
负数乘正数,积为负数;
积的绝对值等于各乘数绝对值的积.
归纳
(-3) × 3 =_______.
(-3) × 2 =_______.
(-3) × 1 =_______.
(-3) × 0 =_______.
思考
随着第二个乘数逐次递减1,积逐次增加3.
利用上面归纳的结论计算下面的算式,你发现有什么规律
-9
-6
-3
0
按照上述规律,填空.你发现了什么规律
3
6
9
随着第二个乘数逐次递减1,积逐次增加3.
(-3)× (-1) =_______.
(-3)× (-2) =_______.
(-3)× (-3) =_______.
从符号和绝对值两个角度观察下面的算式,你能发现什么规律
(-3) × (-1) = 3.
(-3) × (-2) = 6.
(-3) × (-3) = 9.
负数乘负数,积为正数;
乘积的绝对值等于各乘数绝对值的积.
归纳
归纳
有理数乘法法则:
两数相乘,同号得正、异号得负,并把绝对值相乘.
任何数与0相乘,都得0.
例1 计算
解:(-5)×(-3)...................同号两数相乘
(-5)×(-3)=+( ).......................得正
5×3=15.....................把绝对值相乘
所以(-5)×(-3)=15 .
(1)(-5)×(-3)
(2)(-7)×4
解:(-7)×4........... 异号两数相乘
(-7)×4=-( ).....................得负
7×4=28..........把绝对值相乘
所以(-7)×4=-28.
例2 计算:
(1) (-3)×9; (2) 8×(-1);
要得到一个数的相反数,只要将它乘 -1.
解: (1) (-3)×9=-27;
(2) 8×(-1) =-8;
计算并观察下列式子有何特点?
1
1
1
二、倒数
归纳
有理数中,乘积是1的两个数互为倒数.
如果两个数的乘积是1,那么我们称其中一个数是另一个数的倒数,并称这两个数互为倒数.
思考:0的倒数是什么呢?
乘积是1的两个数互为倒数.所以0没有倒数.
例如,我们说 与2互为倒数.2是 的倒数,
是2的倒数.
(1)数a(a≠0)的倒数是什么
(a≠0时,a的倒数是 )
(2)分数-(m≠0,n≠0)的倒数是什么?
把这个分数的分子和分母交换位置,即-的倒数为 -
思考
例3 求下列各数的倒数:
(1)- ;(2)0.125;(3)-1 ;(4)1;(5) 3 .
解:(1) 的倒数是
(2) 0.125= 0.125的倒数是8.
(3) -1的倒数是1.
(4)1的倒数是-1.
(5) 的倒数是 .
1.求小数的倒数,要先把小数化成分数,再求其倒数,
2.倒数等于它本身的数是±1.
3.求带分数的倒数,先把带分数化成假分数,再交换分子和分母的位置.
4.正数的倒数是正数,负数的倒数是负数,0没有倒数.
温馨提示
1.计算:
(1) (-3)×(-4); (2) 3; (3)
解:(1) (-3)×(-4)
=3×4
=12.
(2) 3
=-(3)
=-()
=-12.
(3)=0.
随堂练习
2,说出下列各数的倒数:
1,-1, ,- , (a,b≠0),-5,0.25,
解:(1) 1的倒数是-1.
(2) -1的倒数是1.
(3) - 的倒数是-3.
(4) 的倒数是
(5) -5的倒数是 .
(6) 0.25= .0.25的倒数是4.
乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数同0相乘,都得0.
倒数:乘积是1的两个数互为倒数.
0没有倒数.
有理数
乘法法则
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教七上数学同步精品课件
人教版七年级上册
第一章 有理数
第1课时 有理数的乘法法则(含倒数)
1_4_1有理数的乘法
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1.掌握有理数的乘法法则,并能熟练地进行两个数的乘法运算.
2.会求一个数的倒数.
学习目标
重点
重点
我们已经熟悉正数及0的乘法运算.
与加法类似,引入负数后,将出现 3×(-3),(-3)×3,(-3)×(-3)这样的乘法.
该怎样进行这一类的运算呢?
新课引入
一、有理数的乘法法则
3 × 3 = 9,
3 × 2 = 6,
3 × 1 = 3,
3 × 0 = 0.
思考
随着第二个乘数逐次递减1,积逐次递减3.
观察下面的乘法算式,你能发现什么规律吗
新知学习
3×(-1)=-3,
3×(-2)=_______.
3×(-3)=_______.
-6
-9
随着第二个乘数逐次递减1,积逐次递减3.
要使这个规律在引入负数后仍然成立,那么应有:
3 × 3 = 9,
2 × 3 = 6,
1 × 3 = 3,
0 × 3 = 0.
思考
随着第一个乘数逐次递减1,积逐次递减3.
观察下面的算式,你又能发现什么规律
要使这个规律在引入负数后仍然成立,那么应有:
(-1)×3=-3,
(-2)×3=_______.
(-3)×3=_______.
-6
-9
随着第一个乘数逐次递减1,积逐次递减3.
从符号和绝对值两个角度观察上述4个算式,你能发现什么规律
正数×正数 =正数
3 × 3 = 9,
3 × 2 = 6,
3 × 1 = 3,
3 × 0 = 0.
3× (-1)= -3,
3× (-2)= -6.
3× (-3)= -9.
3 × 3 = 9,
2 × 3 = 6,
1 × 3 = 3,
0 × 3 = 0.
(-1) ×3= -3,
(-2) ×3= -6.
(-3) ×3= -9.
正数×负数 =负数
正数×正数 =正数
负数×正数 =负数
积的绝对值=各乘数绝对值的积.
正数乘正数,积为正数;
正数乘负数,积为负数;
负数乘正数,积为负数;
积的绝对值等于各乘数绝对值的积.
归纳
(-3) × 3 =_______.
(-3) × 2 =_______.
(-3) × 1 =_______.
(-3) × 0 =_______.
思考
随着第二个乘数逐次递减1,积逐次增加3.
利用上面归纳的结论计算下面的算式,你发现有什么规律
-9
-6
-3
0
按照上述规律,填空.你发现了什么规律
3
6
9
随着第二个乘数逐次递减1,积逐次增加3.
(-3)× (-1) =_______.
(-3)× (-2) =_______.
(-3)× (-3) =_______.
从符号和绝对值两个角度观察下面的算式,你能发现什么规律
(-3) × (-1) = 3.
(-3) × (-2) = 6.
(-3) × (-3) = 9.
负数乘负数,积为正数;
乘积的绝对值等于各乘数绝对值的积.
归纳
归纳
有理数乘法法则:
两数相乘,同号得正、异号得负,并把绝对值相乘.
任何数与0相乘,都得0.
例1 计算
解:(-5)×(-3)...................同号两数相乘
(-5)×(-3)=+( ).......................得正
5×3=15.....................把绝对值相乘
所以(-5)×(-3)=15 .
(1)(-5)×(-3)
(2)(-7)×4
解:(-7)×4........... 异号两数相乘
(-7)×4=-( ).....................得负
7×4=28..........把绝对值相乘
所以(-7)×4=-28.
例2 计算:
(1) (-3)×9; (2) 8×(-1);
要得到一个数的相反数,只要将它乘 -1.
解: (1) (-3)×9=-27;
(2) 8×(-1) =-8;
计算并观察下列式子有何特点?
1
1
1
二、倒数
归纳
有理数中,乘积是1的两个数互为倒数.
如果两个数的乘积是1,那么我们称其中一个数是另一个数的倒数,并称这两个数互为倒数.
思考:0的倒数是什么呢?
乘积是1的两个数互为倒数.所以0没有倒数.
例如,我们说 与2互为倒数.2是 的倒数,
是2的倒数.
(1)数a(a≠0)的倒数是什么
(a≠0时,a的倒数是 )
(2)分数-(m≠0,n≠0)的倒数是什么?
把这个分数的分子和分母交换位置,即-的倒数为 -
思考
例3 求下列各数的倒数:
(1)- ;(2)0.125;(3)-1 ;(4)1;(5) 3 .
解:(1) 的倒数是
(2) 0.125= 0.125的倒数是8.
(3) -1的倒数是1.
(4)1的倒数是-1.
(5) 的倒数是 .
1.求小数的倒数,要先把小数化成分数,再求其倒数,
2.倒数等于它本身的数是±1.
3.求带分数的倒数,先把带分数化成假分数,再交换分子和分母的位置.
4.正数的倒数是正数,负数的倒数是负数,0没有倒数.
温馨提示
1.计算:
(1) (-3)×(-4); (2) 3; (3)
解:(1) (-3)×(-4)
=3×4
=12.
(2) 3
=-(3)
=-()
=-12.
(3)=0.
随堂练习
2,说出下列各数的倒数:
1,-1, ,- , (a,b≠0),-5,0.25,
解:(1) 1的倒数是-1.
(2) -1的倒数是1.
(3) - 的倒数是-3.
(4) 的倒数是
(5) -5的倒数是 .
(6) 0.25= .0.25的倒数是4.
乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数同0相乘,都得0.
倒数:乘积是1的两个数互为倒数.
0没有倒数.
有理数
乘法法则
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
