2014-2015学年度九年级下学期数学期末考试检测题
文档属性
| 名称 | 2014-2015学年度九年级下学期数学期末考试检测题 |
|
|
| 格式 | zip | ||
| 文件大小 | 483.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-28 00:00:00 | ||
图片预览




文档简介
期末检测题
(本检测题满分:120分,时间:120分钟)
一、选择题(每小题3分,共36分)
1.若抛物线经过点(3,-8)和(-5,-8),则此抛物线的对称轴是( )
A.x=5 B.x=3 C.x=4 D.x=-l
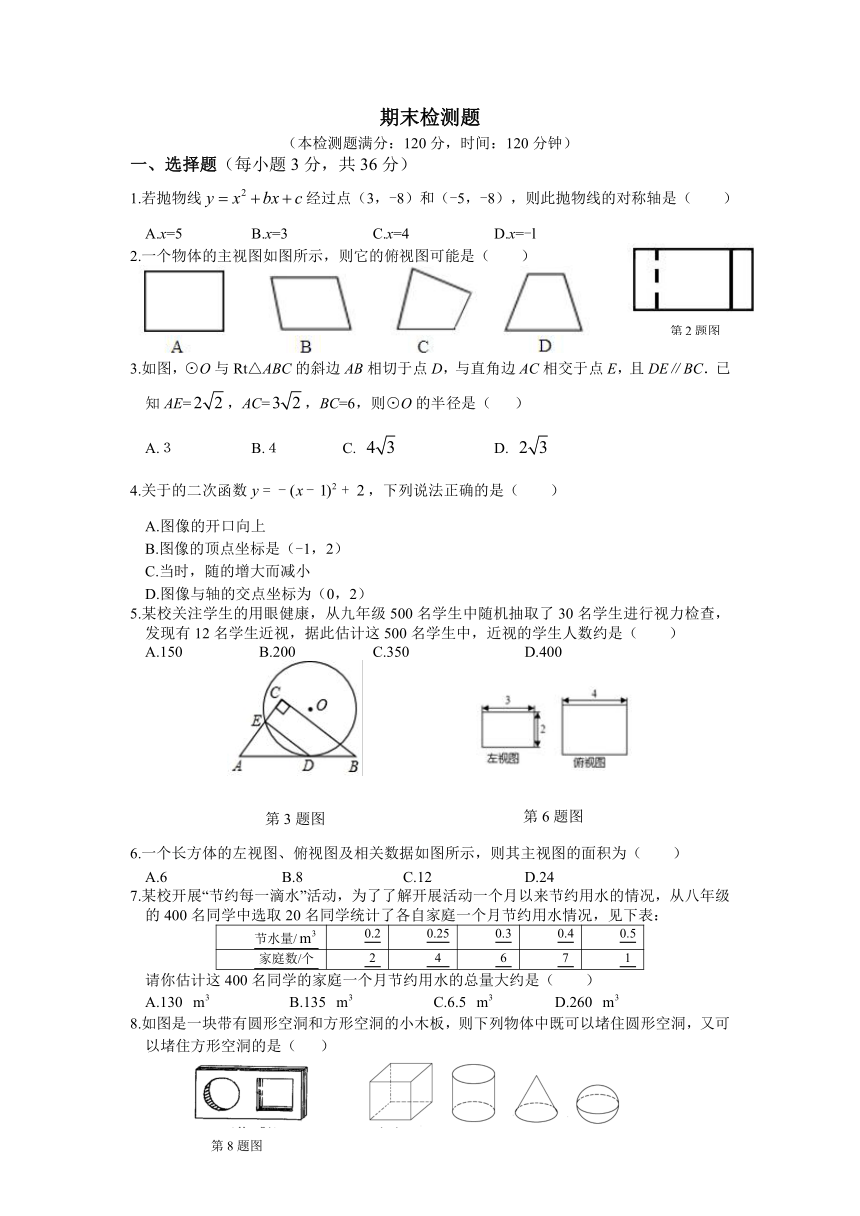
2.一个物体的主视图如图所示,则它的俯视图可能是( )
3.如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于点E,且DE∥BC.已知AE=,AC=,BC=6,则⊙O的半径是( )
A.3 B.4 C. D.
4.关于的二次函数,下列说法正确的是( )
A.图像的开口向上
B.图像的顶点坐标是(-1,2)
C.当时,随的增大而减小
D.图像与轴的交点坐标为(0,2)
5.某校关注学生的用眼健康,从九年级500名学生中随机抽取了30名学生进行视力检查,发现有12名学生近视,据此估计这500名学生中,近视的学生人数约是( )
A.150 B.200 C.350 D.400
6.一个长方体的左视图、俯视图及相关数据如图所示,则其主视图的面积为( )
A.6 B.8 C.12 D.24
7.某校开展“节约每一滴水”活动,为了了解开展活动一个月以来节约用水的情况,从八年级的400名同学中选取20名同学统计了各自家庭一个月节约用水情况,见下表:
节水量/ 0.2 0.25 0.3 0.4 0.5
家庭数/个 2 4 6 7 1
请你估计这400名同学的家庭一个月节约用水的总量大约是( )
A.130 B.135 C.6.5 D.260
8.如图是一块带有圆形空洞和方形空洞的小木板,则下列物体中既可以堵住圆形空洞,又可
以堵住方形空洞的是( )
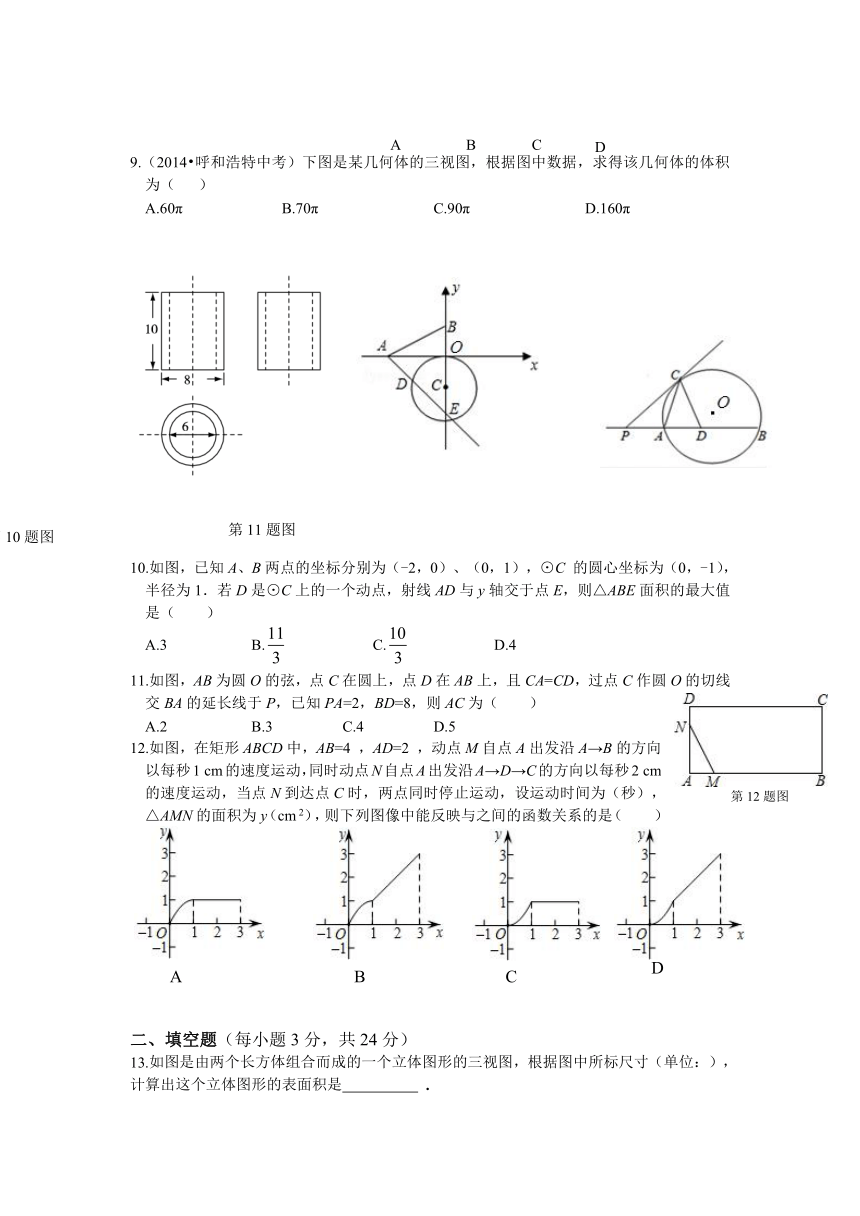
9.(2014 呼和浩特中考)下图是某几何体的三视图,根据图中数据,求得该几何体的体积为( )
A.60π B.70π C.90π D.160π
10.如图,已知A、B两点的坐标分别为(-2,0)、(0,1),⊙C 的圆心坐标为(0,-1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是( )
A.3 B. C. D.4
11.如图,AB为圆O的弦,点C在圆上,点D在AB上,且CA=CD,过点C作圆O的切线交BA的延长线于P,已知PA=2,BD=8,则AC为( )
A.2 B.3 C.4 D.5
12.如图,在矩形ABCD中,AB=4 ,AD=2 ,动点M自点A出发沿A→B的方向以每秒1 cm的速度运动,同时动点N自点A出发沿A→D→C的方向以每秒2 cm的速度运动,当点N到达点C时,两点同时停止运动,设运动时间为(秒),△AMN的面积为y(cm 2),则下列图像中能反映与之间的函数关系的是( )
二、填空题(每小题3分,共24分)
13.如图是由两个长方体组合而成的一个立体图形的三视图,根据图中所标尺寸(单位:),计算出这个立体图形的表面积是 .
14.从某玉米种子中抽取6批,在同一条件下进行发芽实验,有关数据如下:
种子粒数 100 400 800 1 000 2 000 5 000
发芽种子粒数 85 318 652 793 1 604 4 005
发芽频率 0.850 0.795 0.815 0.793 0.802 0.801
根据以上数据可以估计,该玉米种子发芽的概率约为_________(精确到0.1).
15.抛物线=与直线=1,=2,=1,=2组成的正方形有公共点,则的取值范围是 .
16.把抛物线向下平移2个单位,得到的抛物线与轴的交点坐标为 .
17.一个口袋里有25个球,其中红球、黑球、黄球若干个,从口袋中随机摸出一球记下其颜色,再把它放回口袋中摇匀,重复上述过程,共实验200次,其中有120次摸到黄球,由此估计袋中的黄球约有_____个.
18.如图,一根直立于水平地面上的木杆AB在灯光下形成影子,当木杆绕点A按逆时针方向旋转直至到达地面时,影子的长度发生变化.设AB垂直于地面时的影长为AC﹙假定AC>AB﹚,影长的最大值为m,最小值为n,那么下列结论:①m>AC;②m=AC;③n=AB;④影子的长度先增大后减小.其中,正确结论的序号是________.
19.如图,过⊙O上一点C作⊙O的切线,交⊙O直径AB的延长线于点D.若∠D=40°,则∠A的度数为_________.
20.如图,在Rt△AOB中,OA=OB=,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线PQ的最小值为________.
三、解答题(共60分)
21.(8分)已知:如图,是⊙的弦,∠,是优弧上的一点,,交延长线于点,连接
(1)求证:是⊙的切线;
(2)若,∠,求⊙的半径
22.(8分)如图是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)根据所示数据计算这个几何体的表面积;
(3)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你求出这个线路的最短路程.
23.(8分)如图,⊙O的直径AB为10 cm,弦BC为5cm,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.
(1)求AC、AD的长;
(2)试判断直线PC与⊙O的位置关系,并说明理由.
24.(8分)一只不透明的袋子中装有2个白球和1个红球,这些球除颜色外都相同.
(1)搅匀后从中一把摸出两个球,请通过列表或画树状图求两个球都是白球的概率;
(2)搅匀后从中任意摸出一个球,要使摸出红球的概率为,应如何添加红球?
25.(8分)在一个不透明的布袋里装有4个标有1,2,3,4的小球,它们的形状、大小完全相同,小明从布袋里随机取出一个小球,记下数字为x,小红在剩下的3个小球中随机取出一个小球,记下数字为y.
(1)计算由x、y确定的点(x,y)在函数y=-x+5的图象上的概率.
(2)小明和小红约定做一个游戏,其规则为:若x、y满足xy>6则小明胜,若x、y满足xy<6则小红胜,这个游戏公平吗?说明理由.若不公平,请写出公平的游戏规则.
26.(10分)如图,某隧道横截面的上下轮廓线分别由抛物线对称的一部分和矩形的一部分构成,最大高度为6米,底部宽度为12米.现以O点为原点,OM所在直线为轴建立直角坐标系.
(1)直接写出点M及抛物线顶点P的坐标;
(2)求出这条抛物线的函数解析式;
(3)若要搭建一个矩形“支撑架”ADCB,使C、D点在抛物线上,A、B点在地面OM上,这个“支撑架”总长的最大值是多少?
27.(10分)如图所示,抛物线经过原点O,与轴交于另一点N,直线与两坐标轴分别交于A、D两点,与抛物线交于B(1,3)、C(2,2)两点.
(1)求直线与抛物线的解析式.
(2)若抛物线在轴上方的部分有一动点P(,),求△PON面积的最大值.
(3)若动点P保持(2)中的运动路线,问是否存在点P,使得△POA的面积等于△POD 面积的?若存在,请求出点P的坐标;若不存在,请说明理由.
期末检测题参考答案
1.D 解析:∵ 抛物线经过点(3,-8)和(-5,-8),
∴ 此两点关于抛物线的对称轴对称,∴ .故选D.
2.C 解析:从主视图可以看出中间两条线,左边是虚线,右边是实线.只有C满足条件,故选C.
3.D 解析:如图,延长EC交⊙O于点F,连接DF.则根据90°的圆周角所对的弦是直径,得DF是直径.因为DE∥BC,所以△ADE∽△ABC,所以,则DE=4. 在Rt△ADF中,有,根据勾股定理,得,则⊙O的半径是,故选D.
4.C 解析:这个函数图像的顶点是(1,2),
开口向下,对称轴是直线,
在对称轴的左侧随的增大而增大,在对称轴的右侧随的增大而减小.
故选C.
5.B 解析:(人),即近视的学生人数约为200.故选B.
6.B 解析:主视图反映物体的长和高,左视图反映物体的宽和高,俯视图反映物体的长和宽.结合三者之间的关系,从而确定主视图的长和宽分别为4,2,所以面积为8,故选B.
7.A 解析:20名同学各自家庭一个月平均节约用水是(0.2×2+0.25×4+0.3×6+0.4×7+0.5× 1)÷20=0.325(),因此这400名同学的家庭一个月节约用水的总量大约是400×0.325= 130(),故选A.
8.B 解析:根据题意可知该物体的三种视图中有圆和正方形,故由选项可知只有圆柱符合题意.
9.B 解析:由三视图可得该几何体为圆筒,且其底面外径为8,内径为6,该圆筒的高为10,故其体积为
10.B 解析:当射线AD与⊙C相切时,△ABE的面积最大.
连接AC,CD,∵ ∠AOC=∠ADC=90°,AC=AC,OC=CD,
∴ Rt△AOC≌Rt△ADC,∴ AD=AO=2.
设EF=x,∴ .
∵ CF=1,∴ ,∴ △CDE∽△AOE,
∴ ,即,解得x=,
EMBED Equation.DSMT4 \* MERGEFORMAT .故选B.
11.C 解析:如图,连接BC,∵ CA=CD,∴ ∠1=∠2,∴ ∠PAC=∠CDB.∵ PC是⊙O的切线,∴ ∠PCA=∠B,∴ △PAC∽△CDB,∴ .∵ PA=2,BD=8,∴,
∴ AC2=16,∴ AC=4.故选C.
12. D 解析:在矩形ABCD中,AB=4 ,AD=2 cm,
AD+DC=AB+AD=4+2=6 cm.
∵ 点M以每秒1 cm的速度运动,∴ 4÷1=4(秒).
∵ 点N以每秒2 cm的速度运动,∴ 6÷2=3(秒),
∴ 点N先到达终点,运动时间为3秒.
①点N在AD上运动时,(0≤≤1);
②点N在DC上运动时,(1≤3),
∴ 能反映与之间的函数关系的是选项D.
13.200 解析:根据三视图可得:上面的长方体长4 mm,高4 mm,宽2 mm,下面的长方体底面两边长分别为6 mm、8 mm,高2 mm,∴ 立体图形的表面积是:4×4×2+4×2×2+4×2+6×2×2+8×2×2+6×8×2-4×2=200(mm 2).
14. 解析:由表知,种子发芽的频率在0.8左右摆动,并且随着统计量的增加这种规律逐渐明显,所以可以把0.8作为该玉米种子发芽概率的估计值.
15. 解析:如图,四条直线=1,=2,=1,=2围成正方形ABCD,
因为抛物线与正方形有公共点,所以可得>0,而且值越大,抛物线开口越小,
因此当抛物线分别过点A(1,2),C(2,1)时,
分别取得最大值与最小值,代入计算得出:=2,=.由此得出的取值范围是.
16.(0,-1) 解析:由题意得原抛物线的顶点坐标为(2,-3),∴ 新抛物线的顶点坐标为(2,-5),
∴ 新抛物线的解析式为,
∴ 抛物线与轴的交点坐标为(0,-1).
17.15 解析:因为口袋里有25个球,实验200次,其中有120次摸到黄球,所以摸到黄球的频率为,所以袋中的黄球有(个).
18.①③④ 解析:当木杆绕点A按逆时针方向旋转时,如图所示,当AB与光线BC垂直时,m最大,则m>AC,①成立;①成立,那么②不成立;最小值为AB与AC重合,故n=AB,故③成立;由上可知,影子的长度先增大后减小,④成立.
19.25° 解析:如图,连接OC,∵ CD切⊙O于C,∴ OC⊥CD,∴ ∠OCD=90°.
∵ ∠D=40°,∴ ∠COD=180°-90°-40°=50°.∵ OA=OC,∴ ∠A=∠OCA.
∵ ∠A+∠OCA=∠COD=50°,∴ ∠A=25°.
20. 解析:如图,连接OP、OQ.∵ PQ是⊙O的切线,∴ OQ⊥PQ.
根据勾股定理知,∴ 当PO⊥AB时,线段PQ最短.
∵ 在Rt△AOB中,OA=OB=,∴ AB=OA=6,
∴ ,∴ .
21.(1)证明:连接则∠∠.
因为∥,所以∠∠,
所以∠,所以是⊙O的切线
(2)解:因为∠,∠,所以∠
延长交于点连接∠
在Rt△,∠,所以所以⊙O的半径为
22.解:(1)根据三视图的知识,主视图以及左视图都是三角形,俯视图为圆形,故可判断出该几何体是圆锥.
(2)表面积(平方厘米),即该几何体的表面积为16π平方厘米.
(3)如图,将圆锥侧面展开,得到扇形ABB′,则线段BD为所求的最短路程.
设∠BAB′=n°.∵ ,∴ n=120,即∠BAB′=120°.
∵ C为弧BB′中点,∴ ∠ADB=90°,∠BAD=60°,
∴,
∴ 路线的最短路程为cm.
23.解:(1)如图,连接BD,∵ AB是直径,∴ ∠ACB=∠ADB=90°.
在Rt△ABC中,AC===8.
∵ CD平分∠ACB,∴ AD=BD,∴ Rt△ABD是直角等腰三角形,
∴ AD=AB=×10=5cm.
(2)直线PC与⊙O相切,理由:连接OC,
∵ OC=OA,∴ ∠CAO=∠OCA.
∵ PC=PE,∴ ∠PCE=∠PEC.
∵ ∠PCE=∠PCB+∠ECB,∠PEC=∠CAE+∠ACE,
∠ACE=∠ECB,∴ ∠PCB=∠CAE =∠ACO.
∵ ∠ACB=90°,∴ ∠OCP=∠OCB+∠PCB=∠ACO+∠OCB=∠ACB=90°,
∴ OC⊥PC,∴ 直线PC与⊙O相切.
24.解:(1)树状图如图:
P(两个球都是白球).
(2)(方法一)设应添加x个红球,由题意得,
解得x=3.经检验,x=3是原方程的解.
答:应添加3个红球.
(方法二)添加后P(摸出红球)
添加后P(摸出白球)
添加后球的总个数.
应添加6-3=3个红球.
25.解:(1)画树状图得:
∵ 共有12种等可能的结果,在函数y=-x+5的图像上的有:(1,4),(2,3),(3,2),(4,1),∴ 点(x,y)在函数y=-x+5的图像上的概率为:.
(2)∵ x、y满足xy>6有:(2,4),(3,4),(4,2),(4,3)共4种情况,x、y满足xy<6有(1,2),(1,3),(1,4),(2,1),(3,1),(4,1)共6种情况,
∴,,
∴ P(小明胜)≠P(小红胜),∴ 不公平.
公平的游戏规则为:若x、y满足xy≥6则小明胜,若x、y满足xy<6则小红胜.
26. 解:(1) M(12,0),P(6,6).
(2) 设此函数解析式为.
∵ 函数的图像经过点(0,3),
∴ ,即.
∴ 此函数解析式为.
(3) 设A(,0),则B(12-,0),
C,D.
∴“支撑架”总长AD+DC+CB=
=.
∵ 此二次函数的图像开口向下,
∴ 当 时,AD+DC+CB有最大值为18.
27. 分析:(1)把点B、C的坐标代入直线解析式解方程组即可得解,把点B、C、O的坐标代入抛物线的解析式,解方程组求出的值,即可得到抛物线的解析式.
(2)先根据抛物线的解析式求出点N的坐标,再根据三角形的面积公式可知,点P为抛物线的顶点时△PON底边ON上的高最大,面积最大,求出点P的纵坐标,代入面积公式即可得解.
(3)先求出点A、D的坐标,再设点P的坐标为(,),根据三角形的面积公式列式得到关于的一元二次方程,然后求出方程的解,再根据点P在轴的上方进行 判断.
解:(1)根据题意,得解得
∴ 直线的解析式是.
根据图像,抛物线经过点B(1,3)、C(2,2)、O(0,0),
∴解得
∴ 抛物线的解析式是.
(2)当时,,解得,,∴ 点N的坐标是(2.5 ,0).
∵ 点P的纵坐标越大,△PON的面积越大,
当点P是抛物线的顶点时,△PON的面积最大,
此时,
.
(3)由(1)知直线的解析式是当=0时,=4,
当=0时,-+4=0,解得=4,∴ 点A、D的坐标是A(0,4)、D(4,0).
设点P的坐标是(,),则
,
整理得,解得=0,=-2,
此时点P不在轴的上方,不符合题意,
∴ 不存在点P,使得△POA的面积等于△POD面积的.
第2题图
第6题图
第3题图
第8题图
A
B
C
D
第11题图
第10题图
第9题图
第12题图
D
C
B
A
第14题图
第20题图
第19题图
第18题图
第21题图
第22题图
第23题图
第27题图
第26题图
第3题答图
第10题答图
第11题答图
第15题答图
第19题答图
第18题答图
第20题答图
第22题答图
第23题答图
第24题答图
第25题答图
(本检测题满分:120分,时间:120分钟)
一、选择题(每小题3分,共36分)
1.若抛物线经过点(3,-8)和(-5,-8),则此抛物线的对称轴是( )
A.x=5 B.x=3 C.x=4 D.x=-l
2.一个物体的主视图如图所示,则它的俯视图可能是( )
3.如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于点E,且DE∥BC.已知AE=,AC=,BC=6,则⊙O的半径是( )
A.3 B.4 C. D.
4.关于的二次函数,下列说法正确的是( )
A.图像的开口向上
B.图像的顶点坐标是(-1,2)
C.当时,随的增大而减小
D.图像与轴的交点坐标为(0,2)
5.某校关注学生的用眼健康,从九年级500名学生中随机抽取了30名学生进行视力检查,发现有12名学生近视,据此估计这500名学生中,近视的学生人数约是( )
A.150 B.200 C.350 D.400
6.一个长方体的左视图、俯视图及相关数据如图所示,则其主视图的面积为( )
A.6 B.8 C.12 D.24
7.某校开展“节约每一滴水”活动,为了了解开展活动一个月以来节约用水的情况,从八年级的400名同学中选取20名同学统计了各自家庭一个月节约用水情况,见下表:
节水量/ 0.2 0.25 0.3 0.4 0.5
家庭数/个 2 4 6 7 1
请你估计这400名同学的家庭一个月节约用水的总量大约是( )
A.130 B.135 C.6.5 D.260
8.如图是一块带有圆形空洞和方形空洞的小木板,则下列物体中既可以堵住圆形空洞,又可
以堵住方形空洞的是( )
9.(2014 呼和浩特中考)下图是某几何体的三视图,根据图中数据,求得该几何体的体积为( )
A.60π B.70π C.90π D.160π
10.如图,已知A、B两点的坐标分别为(-2,0)、(0,1),⊙C 的圆心坐标为(0,-1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是( )
A.3 B. C. D.4
11.如图,AB为圆O的弦,点C在圆上,点D在AB上,且CA=CD,过点C作圆O的切线交BA的延长线于P,已知PA=2,BD=8,则AC为( )
A.2 B.3 C.4 D.5
12.如图,在矩形ABCD中,AB=4 ,AD=2 ,动点M自点A出发沿A→B的方向以每秒1 cm的速度运动,同时动点N自点A出发沿A→D→C的方向以每秒2 cm的速度运动,当点N到达点C时,两点同时停止运动,设运动时间为(秒),△AMN的面积为y(cm 2),则下列图像中能反映与之间的函数关系的是( )
二、填空题(每小题3分,共24分)
13.如图是由两个长方体组合而成的一个立体图形的三视图,根据图中所标尺寸(单位:),计算出这个立体图形的表面积是 .
14.从某玉米种子中抽取6批,在同一条件下进行发芽实验,有关数据如下:
种子粒数 100 400 800 1 000 2 000 5 000
发芽种子粒数 85 318 652 793 1 604 4 005
发芽频率 0.850 0.795 0.815 0.793 0.802 0.801
根据以上数据可以估计,该玉米种子发芽的概率约为_________(精确到0.1).
15.抛物线=与直线=1,=2,=1,=2组成的正方形有公共点,则的取值范围是 .
16.把抛物线向下平移2个单位,得到的抛物线与轴的交点坐标为 .
17.一个口袋里有25个球,其中红球、黑球、黄球若干个,从口袋中随机摸出一球记下其颜色,再把它放回口袋中摇匀,重复上述过程,共实验200次,其中有120次摸到黄球,由此估计袋中的黄球约有_____个.
18.如图,一根直立于水平地面上的木杆AB在灯光下形成影子,当木杆绕点A按逆时针方向旋转直至到达地面时,影子的长度发生变化.设AB垂直于地面时的影长为AC﹙假定AC>AB﹚,影长的最大值为m,最小值为n,那么下列结论:①m>AC;②m=AC;③n=AB;④影子的长度先增大后减小.其中,正确结论的序号是________.
19.如图,过⊙O上一点C作⊙O的切线,交⊙O直径AB的延长线于点D.若∠D=40°,则∠A的度数为_________.
20.如图,在Rt△AOB中,OA=OB=,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线PQ的最小值为________.
三、解答题(共60分)
21.(8分)已知:如图,是⊙的弦,∠,是优弧上的一点,,交延长线于点,连接
(1)求证:是⊙的切线;
(2)若,∠,求⊙的半径
22.(8分)如图是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)根据所示数据计算这个几何体的表面积;
(3)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你求出这个线路的最短路程.
23.(8分)如图,⊙O的直径AB为10 cm,弦BC为5cm,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.
(1)求AC、AD的长;
(2)试判断直线PC与⊙O的位置关系,并说明理由.
24.(8分)一只不透明的袋子中装有2个白球和1个红球,这些球除颜色外都相同.
(1)搅匀后从中一把摸出两个球,请通过列表或画树状图求两个球都是白球的概率;
(2)搅匀后从中任意摸出一个球,要使摸出红球的概率为,应如何添加红球?
25.(8分)在一个不透明的布袋里装有4个标有1,2,3,4的小球,它们的形状、大小完全相同,小明从布袋里随机取出一个小球,记下数字为x,小红在剩下的3个小球中随机取出一个小球,记下数字为y.
(1)计算由x、y确定的点(x,y)在函数y=-x+5的图象上的概率.
(2)小明和小红约定做一个游戏,其规则为:若x、y满足xy>6则小明胜,若x、y满足xy<6则小红胜,这个游戏公平吗?说明理由.若不公平,请写出公平的游戏规则.
26.(10分)如图,某隧道横截面的上下轮廓线分别由抛物线对称的一部分和矩形的一部分构成,最大高度为6米,底部宽度为12米.现以O点为原点,OM所在直线为轴建立直角坐标系.
(1)直接写出点M及抛物线顶点P的坐标;
(2)求出这条抛物线的函数解析式;
(3)若要搭建一个矩形“支撑架”ADCB,使C、D点在抛物线上,A、B点在地面OM上,这个“支撑架”总长的最大值是多少?
27.(10分)如图所示,抛物线经过原点O,与轴交于另一点N,直线与两坐标轴分别交于A、D两点,与抛物线交于B(1,3)、C(2,2)两点.
(1)求直线与抛物线的解析式.
(2)若抛物线在轴上方的部分有一动点P(,),求△PON面积的最大值.
(3)若动点P保持(2)中的运动路线,问是否存在点P,使得△POA的面积等于△POD 面积的?若存在,请求出点P的坐标;若不存在,请说明理由.
期末检测题参考答案
1.D 解析:∵ 抛物线经过点(3,-8)和(-5,-8),
∴ 此两点关于抛物线的对称轴对称,∴ .故选D.
2.C 解析:从主视图可以看出中间两条线,左边是虚线,右边是实线.只有C满足条件,故选C.
3.D 解析:如图,延长EC交⊙O于点F,连接DF.则根据90°的圆周角所对的弦是直径,得DF是直径.因为DE∥BC,所以△ADE∽△ABC,所以,则DE=4. 在Rt△ADF中,有,根据勾股定理,得,则⊙O的半径是,故选D.
4.C 解析:这个函数图像的顶点是(1,2),
开口向下,对称轴是直线,
在对称轴的左侧随的增大而增大,在对称轴的右侧随的增大而减小.
故选C.
5.B 解析:(人),即近视的学生人数约为200.故选B.
6.B 解析:主视图反映物体的长和高,左视图反映物体的宽和高,俯视图反映物体的长和宽.结合三者之间的关系,从而确定主视图的长和宽分别为4,2,所以面积为8,故选B.
7.A 解析:20名同学各自家庭一个月平均节约用水是(0.2×2+0.25×4+0.3×6+0.4×7+0.5× 1)÷20=0.325(),因此这400名同学的家庭一个月节约用水的总量大约是400×0.325= 130(),故选A.
8.B 解析:根据题意可知该物体的三种视图中有圆和正方形,故由选项可知只有圆柱符合题意.
9.B 解析:由三视图可得该几何体为圆筒,且其底面外径为8,内径为6,该圆筒的高为10,故其体积为
10.B 解析:当射线AD与⊙C相切时,△ABE的面积最大.
连接AC,CD,∵ ∠AOC=∠ADC=90°,AC=AC,OC=CD,
∴ Rt△AOC≌Rt△ADC,∴ AD=AO=2.
设EF=x,∴ .
∵ CF=1,∴ ,∴ △CDE∽△AOE,
∴ ,即,解得x=,
EMBED Equation.DSMT4 \* MERGEFORMAT .故选B.
11.C 解析:如图,连接BC,∵ CA=CD,∴ ∠1=∠2,∴ ∠PAC=∠CDB.∵ PC是⊙O的切线,∴ ∠PCA=∠B,∴ △PAC∽△CDB,∴ .∵ PA=2,BD=8,∴,
∴ AC2=16,∴ AC=4.故选C.
12. D 解析:在矩形ABCD中,AB=4 ,AD=2 cm,
AD+DC=AB+AD=4+2=6 cm.
∵ 点M以每秒1 cm的速度运动,∴ 4÷1=4(秒).
∵ 点N以每秒2 cm的速度运动,∴ 6÷2=3(秒),
∴ 点N先到达终点,运动时间为3秒.
①点N在AD上运动时,(0≤≤1);
②点N在DC上运动时,(1≤3),
∴ 能反映与之间的函数关系的是选项D.
13.200 解析:根据三视图可得:上面的长方体长4 mm,高4 mm,宽2 mm,下面的长方体底面两边长分别为6 mm、8 mm,高2 mm,∴ 立体图形的表面积是:4×4×2+4×2×2+4×2+6×2×2+8×2×2+6×8×2-4×2=200(mm 2).
14. 解析:由表知,种子发芽的频率在0.8左右摆动,并且随着统计量的增加这种规律逐渐明显,所以可以把0.8作为该玉米种子发芽概率的估计值.
15. 解析:如图,四条直线=1,=2,=1,=2围成正方形ABCD,
因为抛物线与正方形有公共点,所以可得>0,而且值越大,抛物线开口越小,
因此当抛物线分别过点A(1,2),C(2,1)时,
分别取得最大值与最小值,代入计算得出:=2,=.由此得出的取值范围是.
16.(0,-1) 解析:由题意得原抛物线的顶点坐标为(2,-3),∴ 新抛物线的顶点坐标为(2,-5),
∴ 新抛物线的解析式为,
∴ 抛物线与轴的交点坐标为(0,-1).
17.15 解析:因为口袋里有25个球,实验200次,其中有120次摸到黄球,所以摸到黄球的频率为,所以袋中的黄球有(个).
18.①③④ 解析:当木杆绕点A按逆时针方向旋转时,如图所示,当AB与光线BC垂直时,m最大,则m>AC,①成立;①成立,那么②不成立;最小值为AB与AC重合,故n=AB,故③成立;由上可知,影子的长度先增大后减小,④成立.
19.25° 解析:如图,连接OC,∵ CD切⊙O于C,∴ OC⊥CD,∴ ∠OCD=90°.
∵ ∠D=40°,∴ ∠COD=180°-90°-40°=50°.∵ OA=OC,∴ ∠A=∠OCA.
∵ ∠A+∠OCA=∠COD=50°,∴ ∠A=25°.
20. 解析:如图,连接OP、OQ.∵ PQ是⊙O的切线,∴ OQ⊥PQ.
根据勾股定理知,∴ 当PO⊥AB时,线段PQ最短.
∵ 在Rt△AOB中,OA=OB=,∴ AB=OA=6,
∴ ,∴ .
21.(1)证明:连接则∠∠.
因为∥,所以∠∠,
所以∠,所以是⊙O的切线
(2)解:因为∠,∠,所以∠
延长交于点连接∠
在Rt△,∠,所以所以⊙O的半径为
22.解:(1)根据三视图的知识,主视图以及左视图都是三角形,俯视图为圆形,故可判断出该几何体是圆锥.
(2)表面积(平方厘米),即该几何体的表面积为16π平方厘米.
(3)如图,将圆锥侧面展开,得到扇形ABB′,则线段BD为所求的最短路程.
设∠BAB′=n°.∵ ,∴ n=120,即∠BAB′=120°.
∵ C为弧BB′中点,∴ ∠ADB=90°,∠BAD=60°,
∴,
∴ 路线的最短路程为cm.
23.解:(1)如图,连接BD,∵ AB是直径,∴ ∠ACB=∠ADB=90°.
在Rt△ABC中,AC===8.
∵ CD平分∠ACB,∴ AD=BD,∴ Rt△ABD是直角等腰三角形,
∴ AD=AB=×10=5cm.
(2)直线PC与⊙O相切,理由:连接OC,
∵ OC=OA,∴ ∠CAO=∠OCA.
∵ PC=PE,∴ ∠PCE=∠PEC.
∵ ∠PCE=∠PCB+∠ECB,∠PEC=∠CAE+∠ACE,
∠ACE=∠ECB,∴ ∠PCB=∠CAE =∠ACO.
∵ ∠ACB=90°,∴ ∠OCP=∠OCB+∠PCB=∠ACO+∠OCB=∠ACB=90°,
∴ OC⊥PC,∴ 直线PC与⊙O相切.
24.解:(1)树状图如图:
P(两个球都是白球).
(2)(方法一)设应添加x个红球,由题意得,
解得x=3.经检验,x=3是原方程的解.
答:应添加3个红球.
(方法二)添加后P(摸出红球)
添加后P(摸出白球)
添加后球的总个数.
应添加6-3=3个红球.
25.解:(1)画树状图得:
∵ 共有12种等可能的结果,在函数y=-x+5的图像上的有:(1,4),(2,3),(3,2),(4,1),∴ 点(x,y)在函数y=-x+5的图像上的概率为:.
(2)∵ x、y满足xy>6有:(2,4),(3,4),(4,2),(4,3)共4种情况,x、y满足xy<6有(1,2),(1,3),(1,4),(2,1),(3,1),(4,1)共6种情况,
∴,,
∴ P(小明胜)≠P(小红胜),∴ 不公平.
公平的游戏规则为:若x、y满足xy≥6则小明胜,若x、y满足xy<6则小红胜.
26. 解:(1) M(12,0),P(6,6).
(2) 设此函数解析式为.
∵ 函数的图像经过点(0,3),
∴ ,即.
∴ 此函数解析式为.
(3) 设A(,0),则B(12-,0),
C,D.
∴“支撑架”总长AD+DC+CB=
=.
∵ 此二次函数的图像开口向下,
∴ 当 时,AD+DC+CB有最大值为18.
27. 分析:(1)把点B、C的坐标代入直线解析式解方程组即可得解,把点B、C、O的坐标代入抛物线的解析式,解方程组求出的值,即可得到抛物线的解析式.
(2)先根据抛物线的解析式求出点N的坐标,再根据三角形的面积公式可知,点P为抛物线的顶点时△PON底边ON上的高最大,面积最大,求出点P的纵坐标,代入面积公式即可得解.
(3)先求出点A、D的坐标,再设点P的坐标为(,),根据三角形的面积公式列式得到关于的一元二次方程,然后求出方程的解,再根据点P在轴的上方进行 判断.
解:(1)根据题意,得解得
∴ 直线的解析式是.
根据图像,抛物线经过点B(1,3)、C(2,2)、O(0,0),
∴解得
∴ 抛物线的解析式是.
(2)当时,,解得,,∴ 点N的坐标是(2.5 ,0).
∵ 点P的纵坐标越大,△PON的面积越大,
当点P是抛物线的顶点时,△PON的面积最大,
此时,
.
(3)由(1)知直线的解析式是当=0时,=4,
当=0时,-+4=0,解得=4,∴ 点A、D的坐标是A(0,4)、D(4,0).
设点P的坐标是(,),则
,
整理得,解得=0,=-2,
此时点P不在轴的上方,不符合题意,
∴ 不存在点P,使得△POA的面积等于△POD面积的.
第2题图
第6题图
第3题图
第8题图
A
B
C
D
第11题图
第10题图
第9题图
第12题图
D
C
B
A
第14题图
第20题图
第19题图
第18题图
第21题图
第22题图
第23题图
第27题图
第26题图
第3题答图
第10题答图
第11题答图
第15题答图
第19题答图
第18题答图
第20题答图
第22题答图
第23题答图
第24题答图
第25题答图
同课章节目录
