2023-2024学年人教版数学九年级上册第二十三章旋转单元练习题 (含答案)
文档属性
| 名称 | 2023-2024学年人教版数学九年级上册第二十三章旋转单元练习题 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 291.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-19 18:14:50 | ||
图片预览

文档简介
第二十三章旋转 单元练习题 2023-2024学年人教版数学九年级上册
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
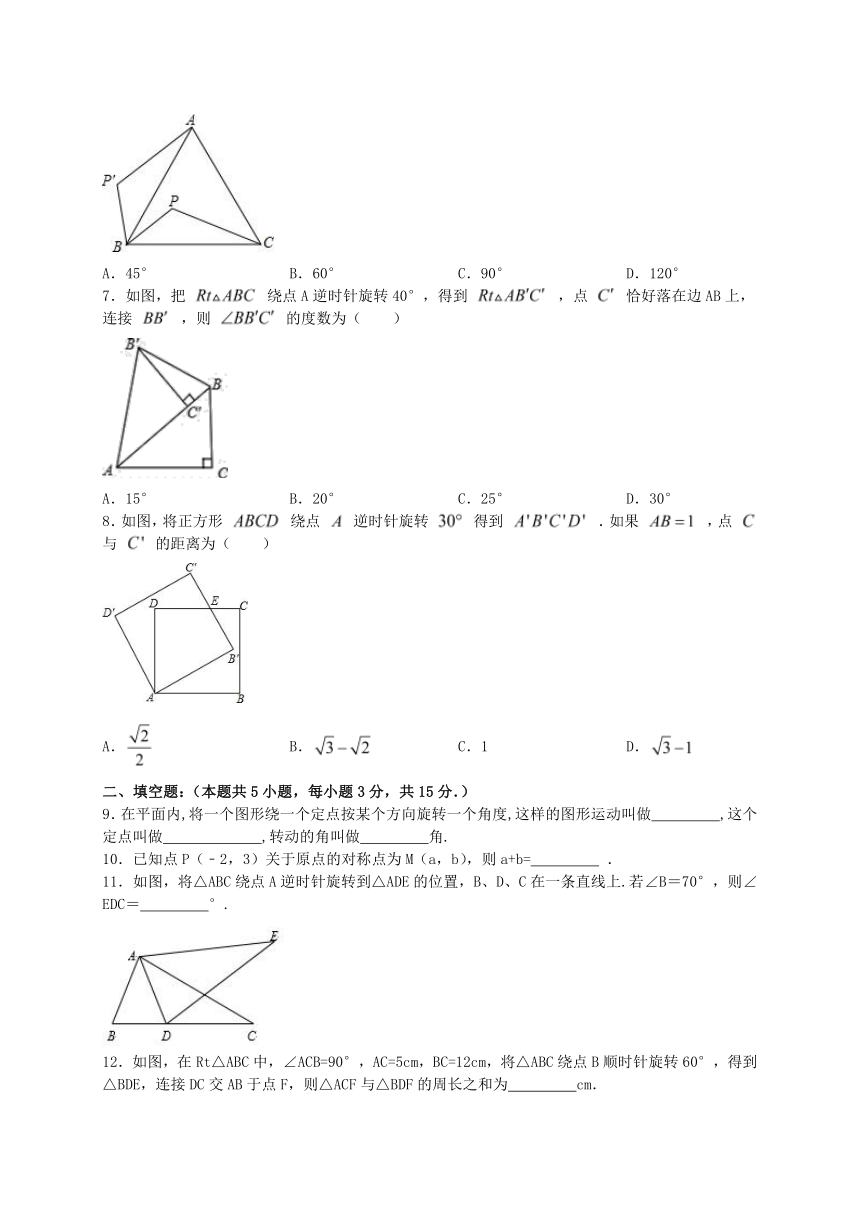
1.下列各图中,不是中心对称图形的是( )
A.①③ B.②④ C.②③ D.①④
2.在平面直角坐标系中,点P(1,2)关于原点对称的点的坐标是( )
A.(﹣1,﹣2) B.(﹣1,2)
C.(1,﹣2) D.(2,1)
3.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有()
A.2种 B.3种 C.4种 D.5种
4.如图,将△ABC绕着点C按顺时针方向旋转20°,B点落在B'位置,A点落在A'位置,若AC⊥A'B',则的度数是( )
A.50° B.60° C.70° D.40°
5.线段MN在直角坐标系中的位置如图所示,将MN绕点M逆时针旋转90°得到线段M1N1,则点N的对应点N1的坐标为( )
A.(0,0) B.(﹣5,﹣4)
C.(﹣3,1) D.(﹣1,﹣3)
6.如图所示,P是等边三角形ABC内的一点,若将三角形PBC绕点B旋转到三角形P′BA,则∠P′BP的度数为( )
A.45° B.60° C.90° D.120°
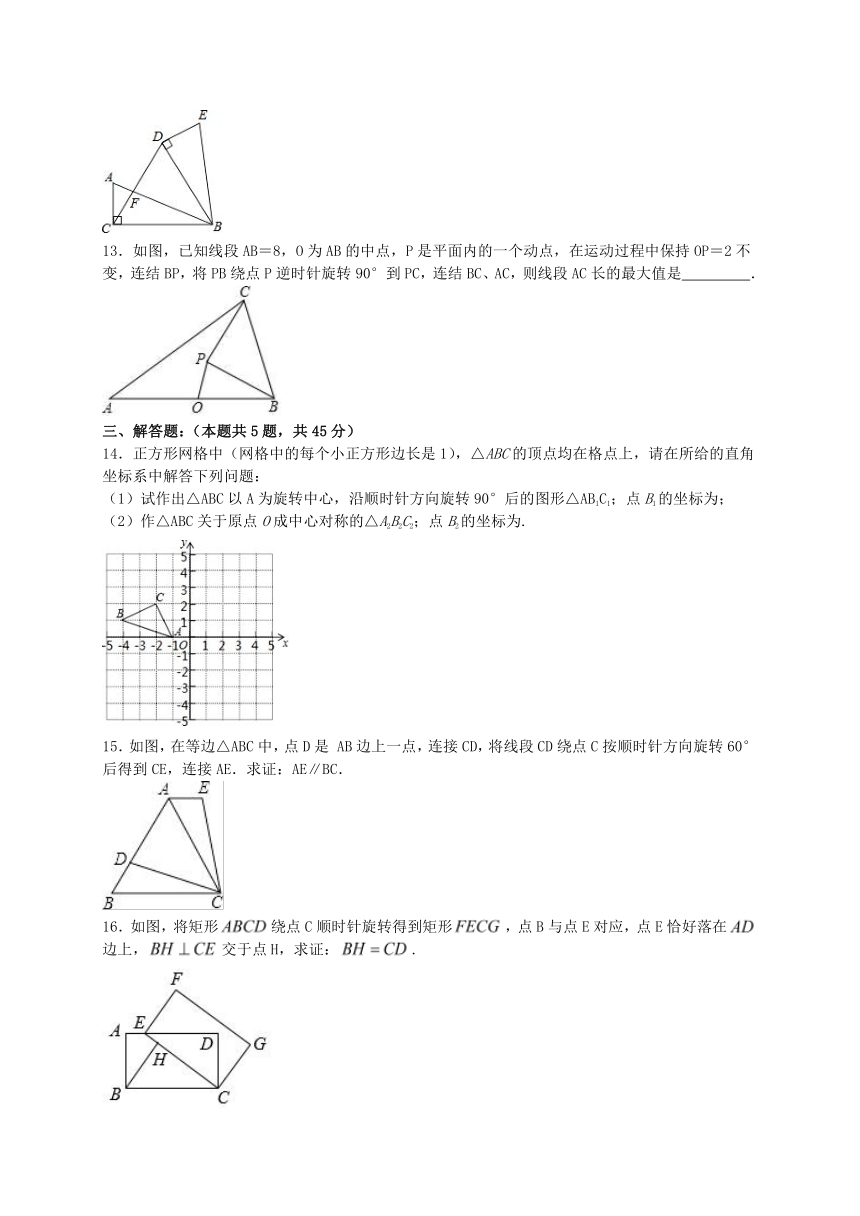
7.如图,把 绕点A逆时针旋转40°,得到 ,点 恰好落在边AB上,连接 ,则 的度数为( )
A.15° B.20° C.25° D.30°
8.如图,将正方形 绕点 逆时针旋转 得到 .如果 ,点 与 的距离为( )
A. B. C.1 D.
二、填空题:(本题共5小题,每小题3分,共15分.)
9.在平面内,将一个图形绕一个定点按某个方向旋转一个角度,这样的图形运动叫做 ,这个定点叫做 ,转动的角叫做 角.
10.已知点P(﹣2,3)关于原点的对称点为M(a,b),则a+b= .
11.如图,将△ABC绕点A逆时针旋转到△ADE的位置,B、D、C在一条直线上.若∠B=70°,则∠EDC= °.
12.如图,在Rt△ABC中,∠ACB=90°,AC=5cm,BC=12cm,将△ABC绕点B顺时针旋转60°,得到△BDE,连接DC交AB于点F,则△ACF与△BDF的周长之和为 cm.
13.如图,已知线段AB=8,O为AB的中点,P是平面内的一个动点,在运动过程中保持OP=2不变,连结BP,将PB绕点P逆时针旋转90°到PC,连结BC、AC,则线段AC长的最大值是 .
三、解答题:(本题共5题,共45分)
14.正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
(1)试作出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;点B1的坐标为;
(2)作△ABC关于原点O成中心对称的△A2B2C2;点B2的坐标为.
15.如图,在等边△ABC中,点D是 AB边上一点,连接CD,将线段CD绕点C按顺时针方向旋转60°后得到CE,连接AE.求证:AE∥BC.
16.如图,将矩形绕点C顺时针旋转得到矩形,点B与点E对应,点E恰好落在边上,交于点H,求证:.
17.如图,在中,,点、分别在、上,,连接,将线段绕点按顺时针方向旋转后得,连接.
(1)求证:;
(2)若,求的度数.
18.正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM
(2)当AE=1时,求EF的长.
参考答案:
1.D 2.A 3.C 4.C 5.C 6.B 7.B 8.D
9.旋转;旋转中心;旋转
10.-1
11.40
12.42
13.
14.(1)解:如下图所示,△AB1C1为所求三角形,点B1的坐标为(0,3);
(2)解:如下图所示,△A2B2C2为所求三角形,点B2的坐标为(4,-1).
15.解:∵△ABC是等边三角形,
∴AC=BC,∠B=∠ACB=60°.
∵线段CD绕点C顺时针旋转60°得到CE,
∴CD=CE,∠DCE=60°,
∴∠DCE=∠ACB,
即∠BCD+∠DCA=∠DCA+∠ACE,
∴∠BCD=∠ACE,
在△BCD与△ACE中,
∴△BCD≌△ACE,
∴∠EAC=∠B=60°,
∴∠EAC=∠ACB,
∴AE∥BC.
16.证明:∵四边形是矩形,
∴,
∴,
∵,
∴,
由旋转得,,
在和中,
,
∴ ,
∴.
17.(1)证明:∵将线段绕点按顺时针方向旋转后得,
∴,,
∵,
∴,
在和中,
,
∴.
(2)解:由(1)可知,
∴,,
∴,
∵,
∴,
∴.
18.(1)证明:∵△DAE逆时针旋转90°得到△DCM,
∴DE=DM ,∠EDM=90°,
∴∠EDF + ∠FDM=90°,
∵∠EDF=45°,
∴∠FDM =∠EDM=45°,
∵DF= DF,
∴△DEF≌△DMF,
∴ EF=MF
(2)解:设EF=x,
∵AE=CM=1 ,
∴ BF=BM-MF=BM-EF=4-x,
∵ EB=2,
在Rt△EBF中,由勾股定理得,
即,
解得,
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.下列各图中,不是中心对称图形的是( )
A.①③ B.②④ C.②③ D.①④
2.在平面直角坐标系中,点P(1,2)关于原点对称的点的坐标是( )
A.(﹣1,﹣2) B.(﹣1,2)
C.(1,﹣2) D.(2,1)
3.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有()
A.2种 B.3种 C.4种 D.5种
4.如图,将△ABC绕着点C按顺时针方向旋转20°,B点落在B'位置,A点落在A'位置,若AC⊥A'B',则的度数是( )
A.50° B.60° C.70° D.40°
5.线段MN在直角坐标系中的位置如图所示,将MN绕点M逆时针旋转90°得到线段M1N1,则点N的对应点N1的坐标为( )
A.(0,0) B.(﹣5,﹣4)
C.(﹣3,1) D.(﹣1,﹣3)
6.如图所示,P是等边三角形ABC内的一点,若将三角形PBC绕点B旋转到三角形P′BA,则∠P′BP的度数为( )
A.45° B.60° C.90° D.120°
7.如图,把 绕点A逆时针旋转40°,得到 ,点 恰好落在边AB上,连接 ,则 的度数为( )
A.15° B.20° C.25° D.30°
8.如图,将正方形 绕点 逆时针旋转 得到 .如果 ,点 与 的距离为( )
A. B. C.1 D.
二、填空题:(本题共5小题,每小题3分,共15分.)
9.在平面内,将一个图形绕一个定点按某个方向旋转一个角度,这样的图形运动叫做 ,这个定点叫做 ,转动的角叫做 角.
10.已知点P(﹣2,3)关于原点的对称点为M(a,b),则a+b= .
11.如图,将△ABC绕点A逆时针旋转到△ADE的位置,B、D、C在一条直线上.若∠B=70°,则∠EDC= °.
12.如图,在Rt△ABC中,∠ACB=90°,AC=5cm,BC=12cm,将△ABC绕点B顺时针旋转60°,得到△BDE,连接DC交AB于点F,则△ACF与△BDF的周长之和为 cm.
13.如图,已知线段AB=8,O为AB的中点,P是平面内的一个动点,在运动过程中保持OP=2不变,连结BP,将PB绕点P逆时针旋转90°到PC,连结BC、AC,则线段AC长的最大值是 .
三、解答题:(本题共5题,共45分)
14.正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
(1)试作出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;点B1的坐标为;
(2)作△ABC关于原点O成中心对称的△A2B2C2;点B2的坐标为.
15.如图,在等边△ABC中,点D是 AB边上一点,连接CD,将线段CD绕点C按顺时针方向旋转60°后得到CE,连接AE.求证:AE∥BC.
16.如图,将矩形绕点C顺时针旋转得到矩形,点B与点E对应,点E恰好落在边上,交于点H,求证:.
17.如图,在中,,点、分别在、上,,连接,将线段绕点按顺时针方向旋转后得,连接.
(1)求证:;
(2)若,求的度数.
18.正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM
(2)当AE=1时,求EF的长.
参考答案:
1.D 2.A 3.C 4.C 5.C 6.B 7.B 8.D
9.旋转;旋转中心;旋转
10.-1
11.40
12.42
13.
14.(1)解:如下图所示,△AB1C1为所求三角形,点B1的坐标为(0,3);
(2)解:如下图所示,△A2B2C2为所求三角形,点B2的坐标为(4,-1).
15.解:∵△ABC是等边三角形,
∴AC=BC,∠B=∠ACB=60°.
∵线段CD绕点C顺时针旋转60°得到CE,
∴CD=CE,∠DCE=60°,
∴∠DCE=∠ACB,
即∠BCD+∠DCA=∠DCA+∠ACE,
∴∠BCD=∠ACE,
在△BCD与△ACE中,
∴△BCD≌△ACE,
∴∠EAC=∠B=60°,
∴∠EAC=∠ACB,
∴AE∥BC.
16.证明:∵四边形是矩形,
∴,
∴,
∵,
∴,
由旋转得,,
在和中,
,
∴ ,
∴.
17.(1)证明:∵将线段绕点按顺时针方向旋转后得,
∴,,
∵,
∴,
在和中,
,
∴.
(2)解:由(1)可知,
∴,,
∴,
∵,
∴,
∴.
18.(1)证明:∵△DAE逆时针旋转90°得到△DCM,
∴DE=DM ,∠EDM=90°,
∴∠EDF + ∠FDM=90°,
∵∠EDF=45°,
∴∠FDM =∠EDM=45°,
∵DF= DF,
∴△DEF≌△DMF,
∴ EF=MF
(2)解:设EF=x,
∵AE=CM=1 ,
∴ BF=BM-MF=BM-EF=4-x,
∵ EB=2,
在Rt△EBF中,由勾股定理得,
即,
解得,
同课章节目录
