2023-2024学年人教版数学八年级上册 13.1轴对称 同步练习题(含答案)
文档属性
| 名称 | 2023-2024学年人教版数学八年级上册 13.1轴对称 同步练习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 339.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-19 20:14:49 | ||
图片预览

文档简介
13.1轴对称 同步练习题 2023-2024学年人教版数学八年级上册
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.下列四个图分别是第24届冬奥会图标中的一部分,其中是轴对称图形的是( )
A. B. C. D.
2.在△ABC中,AB=AC,∠A=36°,AB的中垂线DE交AC于点D,交AB于点E,连接BD,下列论述错误的是( )
A.BD平分∠ABC B.△BDC的周长等于AB+BC
C.AD=BD=BC D.D是AC的中点
3.如图,△ABC和△AB′C′关于直线l对称,下列结论中:①△ABC≌△AB′C′;②∠BAC′=∠B′AC;③直线l垂直平分CC′;④直线BC和B′C′的交点不一定在l上.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
4.如图,在中,AB的垂直平分线交AB于E,交BC于D,连接AD.若,的周长为11cm,则BC的长等于( )
A.5cm B.6cm C.7cm D.8cm
5.如图,在△ABC中,分别以点A和点B为圆心,大于AB长为半径画弧,两弧相交于点M、N,连接MN,交BC于点D,交AB于点E,连接AD.若△ABC的周长等于16,△ADC的周长为9,那么线段AE的长等于( )
A.3 B.3.5 C.5 D.7
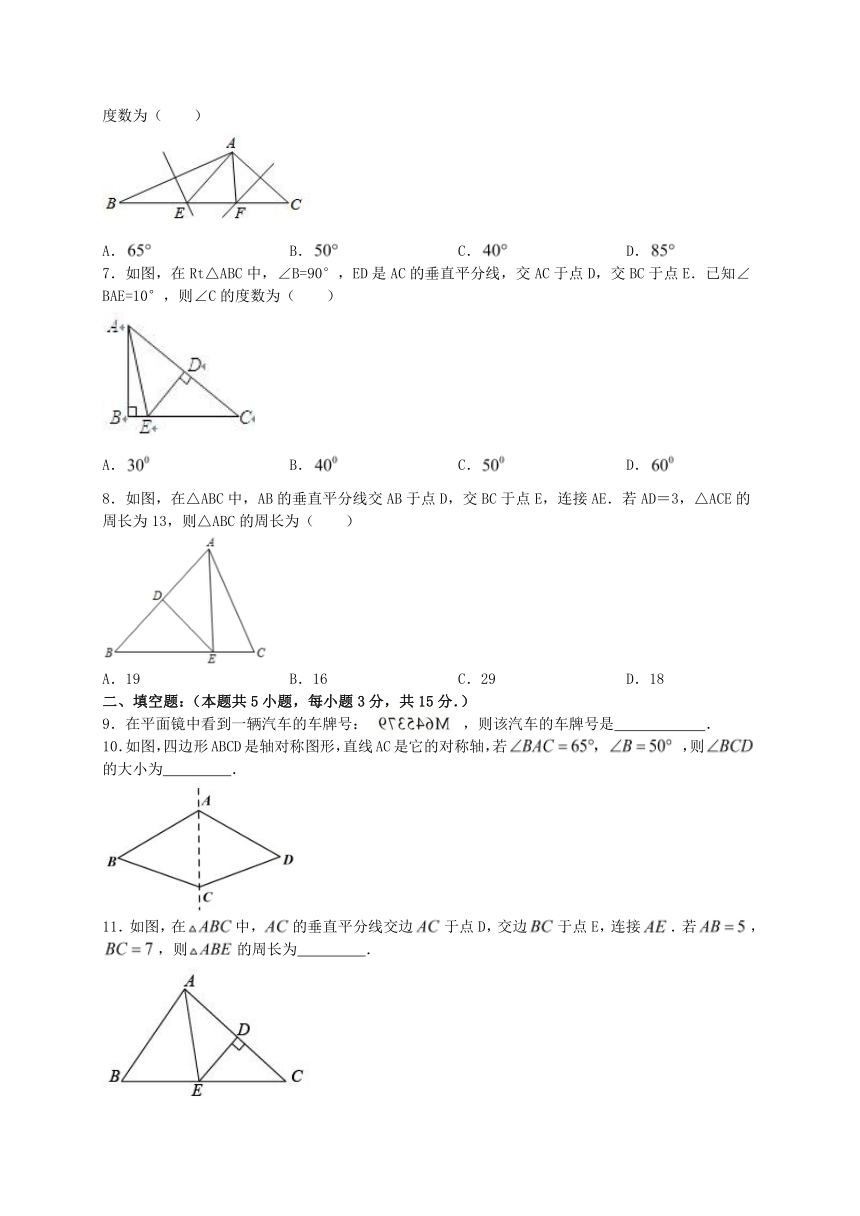
6.如图,中,的垂直平分线分别交于点,则的度数为( )
A. B. C. D.
7.如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠BAE=10°,则∠C的度数为( )
A. B. C. D.
8.如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,连接AE.若AD=3,△ACE的周长为13,则△ABC的周长为( )
A.19 B.16 C.29 D.18
二、填空题:(本题共5小题,每小题3分,共15分.)
9.在平面镜中看到一辆汽车的车牌号: ,则该汽车的车牌号是 .
10.如图,四边形ABCD是轴对称图形,直线AC是它的对称轴,若,则的大小为 .
11.如图,在中,的垂直平分线交边于点D,交边于点E,连接.若,,则的周长为 .
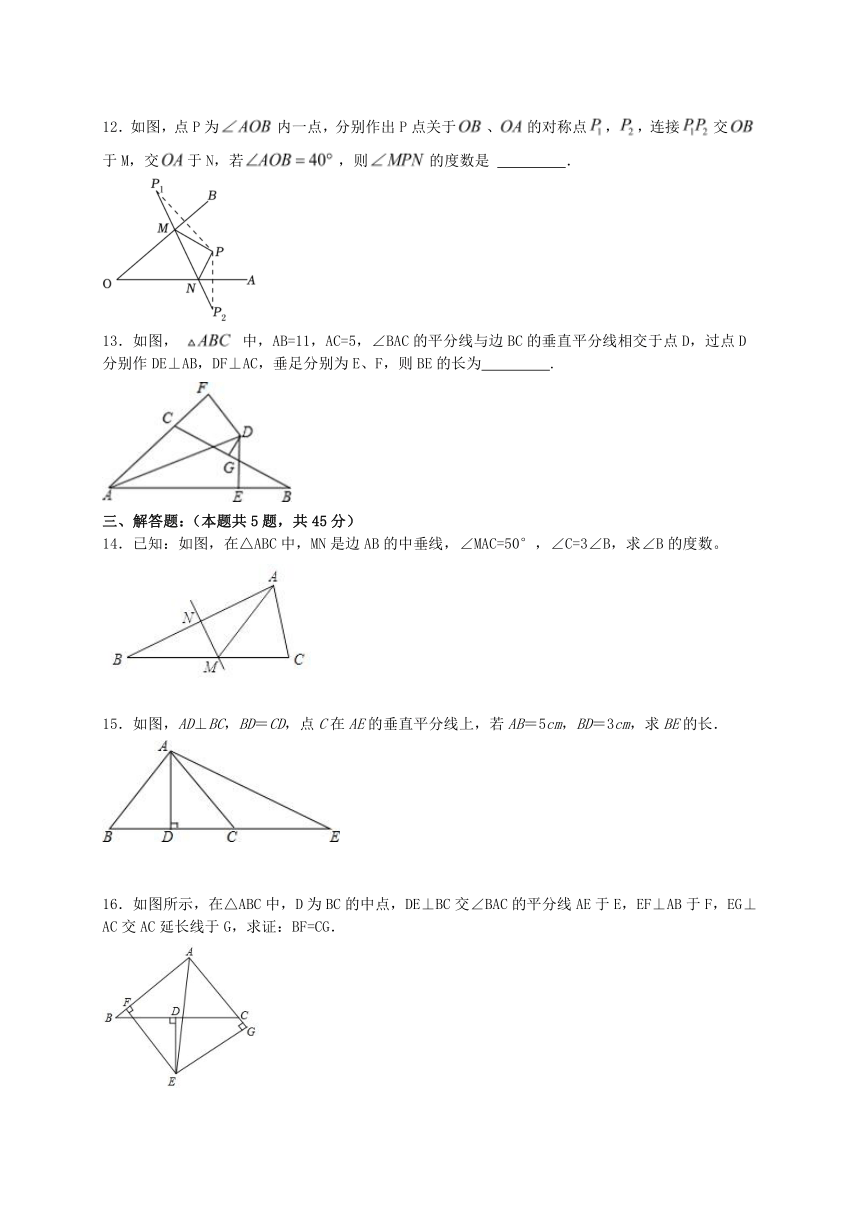
12.如图,点P为内一点,分别作出P点关于、的对称点,,连接交于M,交于N,若,则的度数是 .
13.如图, 中,AB=11,AC=5,∠BAC的平分线与边BC的垂直平分线相交于点D,过点D分别作DE⊥AB,DF⊥AC,垂足分别为E、F,则BE的长为 .
三、解答题:(本题共5题,共45分)
14.已知:如图,在△ABC中,MN是边AB的中垂线,∠MAC=50°,∠C=3∠B,求∠B的度数。
15.如图,AD⊥BC,BD=CD,点C在AE的垂直平分线上,若AB=5cm,BD=3cm,求BE的长.
16.如图所示,在△ABC中,D为BC的中点,DE⊥BC交∠BAC的平分线AE于E,EF⊥AB于F,EG⊥AC交AC延长线于G,求证:BF=CG.
17.如图,在中,,垂足为D,,垂足为E,,与相交于点F.
(1)请说明的理由.
(2)如果,说明的理由.
18.如图,在四边形ABCD中,,E为CD的中点,连接AE、BE,,延长AE交BC的延长线于点F.
(1)请判断FC与AD的数量关系,并说明理由;
(2)若AB=6,AD=2,求BC的长度.
参考答案:
1.A 2.D 3.B 4.C 5.B 6.B 7.B 8.A
9.
10.130°
11.12
12.100°
13.3
14.解:∵MN是边AB的中垂线,
∴AM=BM,
∴∠BAM=∠B.
设∠B=x,则∠BAM=x,
∵∠C=3∠B,∴∠C=3x,
在△ABC中,由三角形内角和定理,得x+x+3x+50°=180°,
∴x=26°,
即∠B=26°.
15.解:∵AD⊥BC,BD=DC,
∴AB=AC;
又∵点C在AE的垂直平分线上,
∴AC=EC,
∴AB=AC=CE=5;
∵BD=CD=3,
∴BE=BD+CD+CE=3+3+5=11cm.
16.解:如图,连接BE、EC,
∵ED⊥BC,
D为BC中点,
∴BE=EC,
∵EF⊥AB EG⊥AG,且AE平分∠FAG,
∴FE=EG,
在Rt△BFE和Rt△CGE中,
,
∴Rt△BFE≌Rt△CGE(HL),
∴BF=CG.
17.(1)证明:∵,,
∴,
又,,
∴;
(2)解:∵,
∴,
∵,
∴,
∴,
又,
∴垂直平分,
∴.
18.(1)解:FC=AD,理由如下:
∵AD∥BC(已知),
∴∠ADC=∠ECF(两直线平行,内错角相等),
∵E是CD的中点(已知),
∴DE=EC(中点的定义).
在△ADE与△FCE中,
,
∴△ADE≌△FCE(ASA),
∴FC=AD(全等三角形的性质);
(2)解:∵△ADE≌△FCE,
∴AE=EF,AD=CF(全等三角形的对应边相等),
∵BE⊥AE,
∴BE是线段AF的垂直平分线,
∴AB=BF=BC+CF,
∴AB=BC+AD,
∵AB=6,AD=2,
∴BC=4
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.下列四个图分别是第24届冬奥会图标中的一部分,其中是轴对称图形的是( )
A. B. C. D.
2.在△ABC中,AB=AC,∠A=36°,AB的中垂线DE交AC于点D,交AB于点E,连接BD,下列论述错误的是( )
A.BD平分∠ABC B.△BDC的周长等于AB+BC
C.AD=BD=BC D.D是AC的中点
3.如图,△ABC和△AB′C′关于直线l对称,下列结论中:①△ABC≌△AB′C′;②∠BAC′=∠B′AC;③直线l垂直平分CC′;④直线BC和B′C′的交点不一定在l上.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
4.如图,在中,AB的垂直平分线交AB于E,交BC于D,连接AD.若,的周长为11cm,则BC的长等于( )
A.5cm B.6cm C.7cm D.8cm
5.如图,在△ABC中,分别以点A和点B为圆心,大于AB长为半径画弧,两弧相交于点M、N,连接MN,交BC于点D,交AB于点E,连接AD.若△ABC的周长等于16,△ADC的周长为9,那么线段AE的长等于( )
A.3 B.3.5 C.5 D.7
6.如图,中,的垂直平分线分别交于点,则的度数为( )
A. B. C. D.
7.如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠BAE=10°,则∠C的度数为( )
A. B. C. D.
8.如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,连接AE.若AD=3,△ACE的周长为13,则△ABC的周长为( )
A.19 B.16 C.29 D.18
二、填空题:(本题共5小题,每小题3分,共15分.)
9.在平面镜中看到一辆汽车的车牌号: ,则该汽车的车牌号是 .
10.如图,四边形ABCD是轴对称图形,直线AC是它的对称轴,若,则的大小为 .
11.如图,在中,的垂直平分线交边于点D,交边于点E,连接.若,,则的周长为 .
12.如图,点P为内一点,分别作出P点关于、的对称点,,连接交于M,交于N,若,则的度数是 .
13.如图, 中,AB=11,AC=5,∠BAC的平分线与边BC的垂直平分线相交于点D,过点D分别作DE⊥AB,DF⊥AC,垂足分别为E、F,则BE的长为 .
三、解答题:(本题共5题,共45分)
14.已知:如图,在△ABC中,MN是边AB的中垂线,∠MAC=50°,∠C=3∠B,求∠B的度数。
15.如图,AD⊥BC,BD=CD,点C在AE的垂直平分线上,若AB=5cm,BD=3cm,求BE的长.
16.如图所示,在△ABC中,D为BC的中点,DE⊥BC交∠BAC的平分线AE于E,EF⊥AB于F,EG⊥AC交AC延长线于G,求证:BF=CG.
17.如图,在中,,垂足为D,,垂足为E,,与相交于点F.
(1)请说明的理由.
(2)如果,说明的理由.
18.如图,在四边形ABCD中,,E为CD的中点,连接AE、BE,,延长AE交BC的延长线于点F.
(1)请判断FC与AD的数量关系,并说明理由;
(2)若AB=6,AD=2,求BC的长度.
参考答案:
1.A 2.D 3.B 4.C 5.B 6.B 7.B 8.A
9.
10.130°
11.12
12.100°
13.3
14.解:∵MN是边AB的中垂线,
∴AM=BM,
∴∠BAM=∠B.
设∠B=x,则∠BAM=x,
∵∠C=3∠B,∴∠C=3x,
在△ABC中,由三角形内角和定理,得x+x+3x+50°=180°,
∴x=26°,
即∠B=26°.
15.解:∵AD⊥BC,BD=DC,
∴AB=AC;
又∵点C在AE的垂直平分线上,
∴AC=EC,
∴AB=AC=CE=5;
∵BD=CD=3,
∴BE=BD+CD+CE=3+3+5=11cm.
16.解:如图,连接BE、EC,
∵ED⊥BC,
D为BC中点,
∴BE=EC,
∵EF⊥AB EG⊥AG,且AE平分∠FAG,
∴FE=EG,
在Rt△BFE和Rt△CGE中,
,
∴Rt△BFE≌Rt△CGE(HL),
∴BF=CG.
17.(1)证明:∵,,
∴,
又,,
∴;
(2)解:∵,
∴,
∵,
∴,
∴,
又,
∴垂直平分,
∴.
18.(1)解:FC=AD,理由如下:
∵AD∥BC(已知),
∴∠ADC=∠ECF(两直线平行,内错角相等),
∵E是CD的中点(已知),
∴DE=EC(中点的定义).
在△ADE与△FCE中,
,
∴△ADE≌△FCE(ASA),
∴FC=AD(全等三角形的性质);
(2)解:∵△ADE≌△FCE,
∴AE=EF,AD=CF(全等三角形的对应边相等),
∵BE⊥AE,
∴BE是线段AF的垂直平分线,
∴AB=BF=BC+CF,
∴AB=BC+AD,
∵AB=6,AD=2,
∴BC=4
