2023-2024学年九年级数学上册(北师大版)4.3相似多边形(课件)(共19张PPT)
文档属性
| 名称 | 2023-2024学年九年级数学上册(北师大版)4.3相似多边形(课件)(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 607.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-19 20:23:34 | ||
图片预览






文档简介
(共19张PPT)
4.3 相似多边形
第四章 图形的相似
学习目标
1)了解相似图形和相似多边形的概念.
2)会根据条件判断两个多边形是否为相似多边形.
3)掌握相似多边形的性质,能根据相似比进行相关的计算.
重点
会根据条件判断两个多边形是否为相似多边形.
难点
掌握相似多边形的性质,能根据相似比进行相关的计算.
观察这两组实例,你发现它们有什么相同点和不同点?
形状相同,大小不同
【提问1】全等图形和相似图形有什么关系呢?
生活中我们会碰到许多这样形状相同,大小不一定相同的图形,在数学上,我们把具有相同形状的图形称为相似形.
相似图形
全等形
全等图形是相似图形的一种特殊形式
【提问2】如果两个图形相似,这两个图形有什么关系呢?
两个图形相似,其中一个图形可以看作由另一个图形_____________得到.
放大或缩小
例1 下列说法中,正确的是( )
A.所有的等腰三角形都相似 B.所有的菱形都相似
C.所有的矩形都相似 D.所有的等腰直角三角形都相似
1. 如图,将图形用放大镜放大,应该属于( ).
A.平移变换 B.相似变换 C.旋转变换 D.对称变换
2. 下列结论中,正确的有:( )
①所有的菱形都相似; ②放大镜下的图形与原图形不一定相似;
③等边三角形都相似; ④有一个角为110度的两个等腰三角形相似;
⑤所有的矩形不一定相似.
A.1个 B.2个 C.3个 D.4个
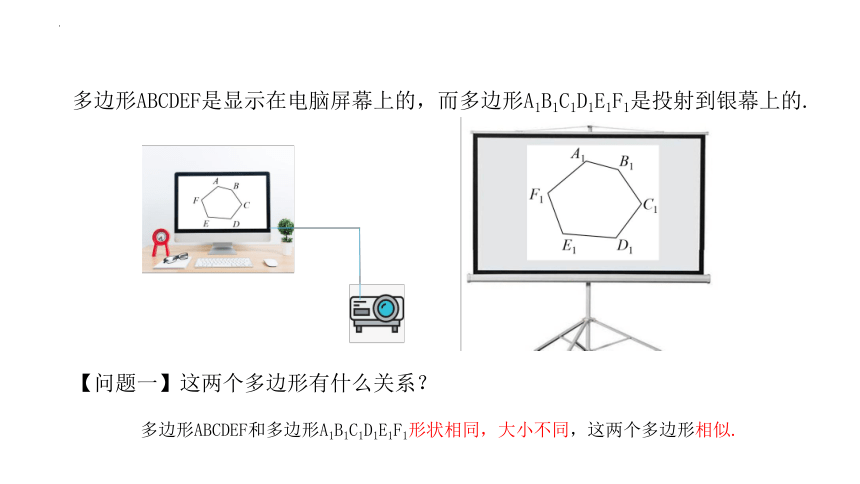
多边形ABCDEF是显示在电脑屏幕上的,而多边形A1B1C1D1E1F1是投射到银幕上的.
【问题一】这两个多边形有什么关系?
多边形ABCDEF和多边形A1B1C1D1E1F1形状相同,大小不同,这两个多边形相似.
多边形ABCDEF是显示在电脑屏幕上的,而多边形A1B1C1D1E1F1是投射到银幕上的.
【问题二】这两个多边形中,是否有对应相等的内角?
∠A与∠A1,∠B与∠B1,∠C与∠C1,∠D与∠D1,∠E与∠E1,∠F与∠F1分别相等
多边形ABCDEF是显示在电脑屏幕上的,而多边形A1B1C1D1E1F1是投射到银幕上的.
【问题三】这两个多边形中,夹相等内角的两边否成比例?
= = = = =
相似多边形概念:
相似多边形的特征:
如果两个边数相同的多边形对应角相等、对应边成比例的两个多边形叫做相似多边形.
相似多边形的对应角相等、对应边成比例.
相似比概念:
相似多边形对应边的比叫做相似比.
相似多边形的表示:
相似多边形用符号“∽”表示,读作“相似于”.
【注意】在记两个相似多边形时,要把表示对应顶点的字母写在对应的位置上.
【问题四】如图,五边形ABCDE∽五边形A’B’C’D’E’ ,它们的角和边有什么关系?
【问题五】若两个相似多边形的相似比为1时,则这两个多边形有什么关系?
∠A=∠A’, ∠B=∠B’, ∠C=∠C’, ∠D=∠D’, ∠E=∠E’
= = = =
这两个多边形是全等多边形
【问题六】根据相似多边形的定义,你知道如何判断相似多边形吗?
1)边数相同;
2)对应角相等;
3)对应边成比例.
以上这三个条件是判定相似多边形必备的条件,缺一不可.
【问题六】任意两个等边三角形相似吗?
∵等边三角形的每个角都为60°且三边都相等
∴两个等边三角形相似(满足边数相等,对应角相等,以及对应边的比相等).
【问题七】任意两个正方形相似吗?
【问题八】任意两个正n边形相似吗?
【问题九】任意两个菱形相似吗?矩形呢?
【问题十】你发现了什么?
相似
相似
不相似,不相似
任意两个边数相等的正多边形都相似.
例2 如图矩形草坪长20m,宽10m,沿草坪四周有1m宽的环形小路,小路内外边缘所构成的矩形EFGH和矩形ABCD是否相似
A
F
E
H
G
D
C
B
解:由题意得,EF=10 ,EH=20,AB=12,AD=22
∴小路内外边缘所构成的矩形EFGH和矩形ABCD不相似
2. 如图所示的两个四边形相似,则α的度数是( )
A.60° B.75° C.87° D.120°
3. 一个多边形的边长为2,3,4,5,6,另一个和它相似的多边形的最长边为24,则这个多边形的最短边长为( )
A.6 B.8 C.12 D.10
4. 一个四边形的边长分别是3,4,5,6,另一个与它形状相同的四边形最短边长为6,则另一个四边形的周长是________.
36
4. 如图,在长为8cm,宽为4cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下矩形的面积是( )
A.2 cm2 B.4 cm2 C.8 cm2 D.16 cm2
【解析】
设留下矩形的宽为xcm,
∵留下的矩形(图中阴影部分)与原矩形相似,
∴,解得
则留下矩形的面积为 .故选C.
5.如图,一个矩形广场的长为90m,宽为60m,广场内有两横,两纵四条小路,且小路内外边缘所围成的两个矩形相似,如果两条横向小路的宽均为1.2m,那么每条纵向小路的宽为__m.
【详解】解:设每条纵向小路的宽为xm,则小路内缘所围成的矩形的长为(90-2x)m,宽为(60-2.4)m,
∵小路内外边缘所围成的两个矩形相似,
∴,
解得,x=1.8
故答案为:1.8
6.已知:如图,梯形ABCD与梯形A′B′C′D′相似,AD∥BC,A′D′∥B′C′,∠A=∠A′.AD=4,A′D′=6,AB=6,B′C′=12.求:
1)梯形ABCD与梯形A′B′C′D′的相似比k;
2)A′B′和BC的长;
3)D′C′∶DC.
【详解】
1)∵梯形ABCD∽梯形A′B′C′D′相似,∴AD:A′D′=4:6=2:3;
2)由(1)知AB: A′B′= AD:A′D′=2:3,
∵AB=6,∴A′B′=9;同理BC=8;
3)∵梯形ABCD∽梯形A′B′C′D′相似,
∴D′C′∶DC= A′D′:AD=3:2.
7.已知矩形ABCD中,AD=3,AB=1.若EF把矩形分成两个小的矩形,如图所示,其中矩形ABEF与矩形ABCD相似,求AF∶AD的值.
【详解】设AF=x,
∵矩形ABEF与矩形ABCD相似,且AD=3,AB=1,
∴对应边成比例,即=,即=,解得x=,
∴AF∶AD=∶3=1∶9.
4.3 相似多边形
第四章 图形的相似
学习目标
1)了解相似图形和相似多边形的概念.
2)会根据条件判断两个多边形是否为相似多边形.
3)掌握相似多边形的性质,能根据相似比进行相关的计算.
重点
会根据条件判断两个多边形是否为相似多边形.
难点
掌握相似多边形的性质,能根据相似比进行相关的计算.
观察这两组实例,你发现它们有什么相同点和不同点?
形状相同,大小不同
【提问1】全等图形和相似图形有什么关系呢?
生活中我们会碰到许多这样形状相同,大小不一定相同的图形,在数学上,我们把具有相同形状的图形称为相似形.
相似图形
全等形
全等图形是相似图形的一种特殊形式
【提问2】如果两个图形相似,这两个图形有什么关系呢?
两个图形相似,其中一个图形可以看作由另一个图形_____________得到.
放大或缩小
例1 下列说法中,正确的是( )
A.所有的等腰三角形都相似 B.所有的菱形都相似
C.所有的矩形都相似 D.所有的等腰直角三角形都相似
1. 如图,将图形用放大镜放大,应该属于( ).
A.平移变换 B.相似变换 C.旋转变换 D.对称变换
2. 下列结论中,正确的有:( )
①所有的菱形都相似; ②放大镜下的图形与原图形不一定相似;
③等边三角形都相似; ④有一个角为110度的两个等腰三角形相似;
⑤所有的矩形不一定相似.
A.1个 B.2个 C.3个 D.4个
多边形ABCDEF是显示在电脑屏幕上的,而多边形A1B1C1D1E1F1是投射到银幕上的.
【问题一】这两个多边形有什么关系?
多边形ABCDEF和多边形A1B1C1D1E1F1形状相同,大小不同,这两个多边形相似.
多边形ABCDEF是显示在电脑屏幕上的,而多边形A1B1C1D1E1F1是投射到银幕上的.
【问题二】这两个多边形中,是否有对应相等的内角?
∠A与∠A1,∠B与∠B1,∠C与∠C1,∠D与∠D1,∠E与∠E1,∠F与∠F1分别相等
多边形ABCDEF是显示在电脑屏幕上的,而多边形A1B1C1D1E1F1是投射到银幕上的.
【问题三】这两个多边形中,夹相等内角的两边否成比例?
= = = = =
相似多边形概念:
相似多边形的特征:
如果两个边数相同的多边形对应角相等、对应边成比例的两个多边形叫做相似多边形.
相似多边形的对应角相等、对应边成比例.
相似比概念:
相似多边形对应边的比叫做相似比.
相似多边形的表示:
相似多边形用符号“∽”表示,读作“相似于”.
【注意】在记两个相似多边形时,要把表示对应顶点的字母写在对应的位置上.
【问题四】如图,五边形ABCDE∽五边形A’B’C’D’E’ ,它们的角和边有什么关系?
【问题五】若两个相似多边形的相似比为1时,则这两个多边形有什么关系?
∠A=∠A’, ∠B=∠B’, ∠C=∠C’, ∠D=∠D’, ∠E=∠E’
= = = =
这两个多边形是全等多边形
【问题六】根据相似多边形的定义,你知道如何判断相似多边形吗?
1)边数相同;
2)对应角相等;
3)对应边成比例.
以上这三个条件是判定相似多边形必备的条件,缺一不可.
【问题六】任意两个等边三角形相似吗?
∵等边三角形的每个角都为60°且三边都相等
∴两个等边三角形相似(满足边数相等,对应角相等,以及对应边的比相等).
【问题七】任意两个正方形相似吗?
【问题八】任意两个正n边形相似吗?
【问题九】任意两个菱形相似吗?矩形呢?
【问题十】你发现了什么?
相似
相似
不相似,不相似
任意两个边数相等的正多边形都相似.
例2 如图矩形草坪长20m,宽10m,沿草坪四周有1m宽的环形小路,小路内外边缘所构成的矩形EFGH和矩形ABCD是否相似
A
F
E
H
G
D
C
B
解:由题意得,EF=10 ,EH=20,AB=12,AD=22
∴小路内外边缘所构成的矩形EFGH和矩形ABCD不相似
2. 如图所示的两个四边形相似,则α的度数是( )
A.60° B.75° C.87° D.120°
3. 一个多边形的边长为2,3,4,5,6,另一个和它相似的多边形的最长边为24,则这个多边形的最短边长为( )
A.6 B.8 C.12 D.10
4. 一个四边形的边长分别是3,4,5,6,另一个与它形状相同的四边形最短边长为6,则另一个四边形的周长是________.
36
4. 如图,在长为8cm,宽为4cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下矩形的面积是( )
A.2 cm2 B.4 cm2 C.8 cm2 D.16 cm2
【解析】
设留下矩形的宽为xcm,
∵留下的矩形(图中阴影部分)与原矩形相似,
∴,解得
则留下矩形的面积为 .故选C.
5.如图,一个矩形广场的长为90m,宽为60m,广场内有两横,两纵四条小路,且小路内外边缘所围成的两个矩形相似,如果两条横向小路的宽均为1.2m,那么每条纵向小路的宽为__m.
【详解】解:设每条纵向小路的宽为xm,则小路内缘所围成的矩形的长为(90-2x)m,宽为(60-2.4)m,
∵小路内外边缘所围成的两个矩形相似,
∴,
解得,x=1.8
故答案为:1.8
6.已知:如图,梯形ABCD与梯形A′B′C′D′相似,AD∥BC,A′D′∥B′C′,∠A=∠A′.AD=4,A′D′=6,AB=6,B′C′=12.求:
1)梯形ABCD与梯形A′B′C′D′的相似比k;
2)A′B′和BC的长;
3)D′C′∶DC.
【详解】
1)∵梯形ABCD∽梯形A′B′C′D′相似,∴AD:A′D′=4:6=2:3;
2)由(1)知AB: A′B′= AD:A′D′=2:3,
∵AB=6,∴A′B′=9;同理BC=8;
3)∵梯形ABCD∽梯形A′B′C′D′相似,
∴D′C′∶DC= A′D′:AD=3:2.
7.已知矩形ABCD中,AD=3,AB=1.若EF把矩形分成两个小的矩形,如图所示,其中矩形ABEF与矩形ABCD相似,求AF∶AD的值.
【详解】设AF=x,
∵矩形ABEF与矩形ABCD相似,且AD=3,AB=1,
∴对应边成比例,即=,即=,解得x=,
∴AF∶AD=∶3=1∶9.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
