数学人教A版(2019)选择性必修第一册2.1.1倾斜角与斜率(共21张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.1.1倾斜角与斜率(共21张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-19 06:00:58 | ||
图片预览







文档简介
(共21张PPT)
高二数学 选择性必修 第一册
第二章 直线和圆的方程
2.1.1 倾斜角与斜率
1、在平面直角坐标系中,结合具体图形,探索确定直线位置的几何要素.(数学抽象)
2、理解直线的倾斜角和斜率的概念.(数学抽象)
3、掌握倾斜角和斜率之间的关系.(逻辑推理)
4、掌握过两点的直线斜率的计算公式.(数学运算)
【高考链接】本节单独命题频率不高,会结合其他知识点进行考查,主要掌握斜率的公式及其应用。
学习目标
下图是自行车“爬坡大师”挑战四川宣汉“山路十八弯”的比赛照片,请问比赛的难度和什么有关?
山路的坡度。
情景引入
1、以下两个楼梯有什么不同?
倾斜程度不同。
2、用什么来刻画呢?
倾斜角/高度与宽度的比值。
情景引入
问题一:在直角坐标系下,确定一条直线的几何要素是什么?
探究一:直线的倾斜角
y
x
.
o
y
x
o
1.一个点能确定一条直线吗?
2.一个方向能确定一条直线吗?
3.一个点和一个方向能确定一条直线吗?
x
y
O
l
A
B
×
×
√
探究小结:确定直线位置的要素除了点之外, 还有直线的方向, 也就是直线的倾斜程度.
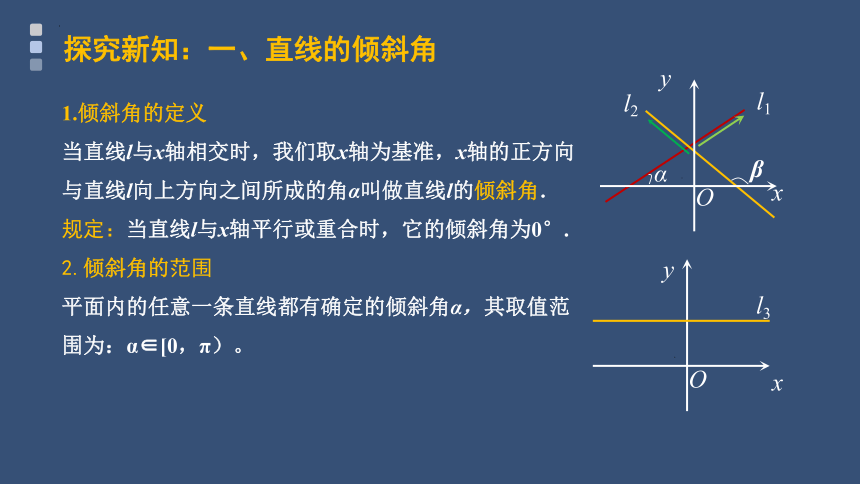
1.倾斜角的定义
当直线l与x轴相交时,我们取x轴为基准,x轴的正方向与直线l向上方向之间所成的角α叫做直线l的倾斜角.
规定:当直线l与x轴平行或重合时,它的倾斜角为0°.
2.倾斜角的范围
平面内的任意一条直线都有确定的倾斜角α,其取值范围为:α∈[0,π)。
探究新知:一、直线的倾斜角
x
y
O
l1
l2
α
β
x
y
O
l3
基础练习
√
×
×
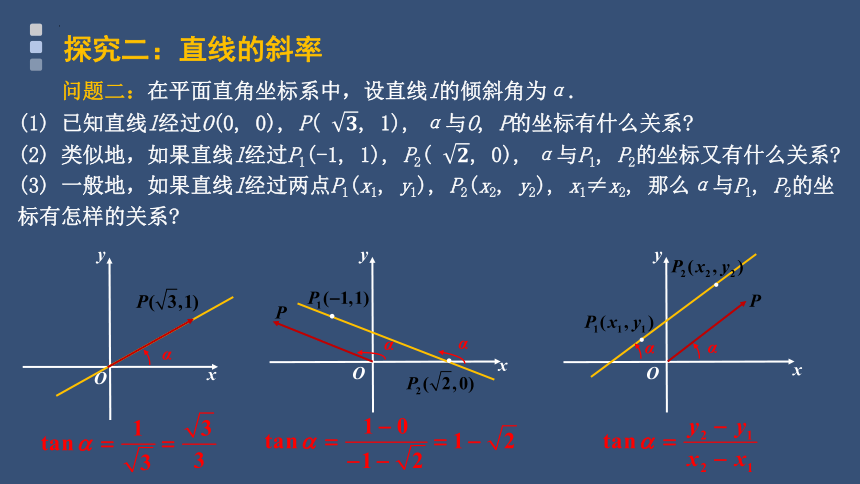
问题二:在平面直角坐标系中,设直线l的倾斜角为α.
(1) 已知直线l经过O(0, 0), P( , 1), α与O, P的坐标有什么关系
(2) 类似地,如果直线l经过P1(-1, 1), P2( , 0), α与P1, P2的坐标又有什么关系
(3) 一般地,如果直线l经过两点P1(x1, y1), P2(x2, y2), x1≠x2, 那么α与P1, P2的坐标有怎样的关系
探究二:直线的斜率
O
y
x
α
O
y
x
α
α
O
y
x
α
α
1.直线斜率的定义
我们把一条直线的的倾斜角α的正切值叫做这条直线的斜率(slope).斜率通常用小写字母k 表示,即:
k =tanα
注:倾斜角是90 °的直线没有斜率。
探究新知:二、直线的斜率
2.直线斜率的公式
综上所述,我们得到经过两点P1(x1,y1),P2(x2,y2)(x1≠x2)的直线斜率公式:
探究新知:二、直线的斜率
思考1:上述公式与P1,P2两点的顺序有关吗?
无关。
思考2:当直线P1P2与x轴平行或重合时,公式还成立吗?
成立。
思考3:当直线P1P2与y轴平行或重合时,公式还成立吗?
不成立。
探究新知:二、直线的斜率
探究新知:二、直线的斜率
【补充】
倾斜角α 0° 30° 45° 60° 120° 135° 150°
斜率k
3.倾斜角与斜率的变化关系
思考讨论:直线的倾斜角增大时,斜率如何变化
α∈[0°,90°)时,倾斜角越大,斜率越大;
α∈(90°,180°)时,倾斜角越大,斜率越大.
【提示】斜率范围:(-∞,+∞)
探究新知:二、直线的斜率
0°<α< 90°
α= 90°
90°< α <180°
α= 0°
k=0
k >0
k不存在
k<0
4.方向向量与斜率的关系
令P1P2=(x2-x1,y2-y1)
=(x,y)
则tanα = = =
探究新知:二、直线的斜率
【例1】如图2.1-6,已知A(3, 2),B(-4, 1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
教材例题
下列说法中,正确的是 ( )
A. 直线的倾斜角为α,则此直线的斜率为tanα
B. 直线的斜率为tanα,则此直线的倾斜角为α
C. 若直线的倾斜角为α,则sinα>0
D. 任意直线都有倾斜角α,且α ≠ 90°时,斜率为tanα
基础练习
D
一、直线的倾斜角
当堂小结
二、、斜率、坐标、方向向量间的关系
三、知识梳理
当堂小结
【题型一】已知经过A(m,2), B(-m,2m-1)的直线的倾斜角为α, 且45°<α<135°, 试求实数m的取值范围.
解:
思维拓展
【题型二】已知M,N坐标分别是(2,-3),(-3,-2),直线L经过点P(1,1)且与线段MN相交,求直线L的斜率k的范围.
思维拓展
O
x
y
P(1,1)
M(2,-3)
N(-3,-2)
高二数学 选择性必修 第一册
第二章 直线和圆的方程
2.1.1 倾斜角与斜率
1、在平面直角坐标系中,结合具体图形,探索确定直线位置的几何要素.(数学抽象)
2、理解直线的倾斜角和斜率的概念.(数学抽象)
3、掌握倾斜角和斜率之间的关系.(逻辑推理)
4、掌握过两点的直线斜率的计算公式.(数学运算)
【高考链接】本节单独命题频率不高,会结合其他知识点进行考查,主要掌握斜率的公式及其应用。
学习目标
下图是自行车“爬坡大师”挑战四川宣汉“山路十八弯”的比赛照片,请问比赛的难度和什么有关?
山路的坡度。
情景引入
1、以下两个楼梯有什么不同?
倾斜程度不同。
2、用什么来刻画呢?
倾斜角/高度与宽度的比值。
情景引入
问题一:在直角坐标系下,确定一条直线的几何要素是什么?
探究一:直线的倾斜角
y
x
.
o
y
x
o
1.一个点能确定一条直线吗?
2.一个方向能确定一条直线吗?
3.一个点和一个方向能确定一条直线吗?
x
y
O
l
A
B
×
×
√
探究小结:确定直线位置的要素除了点之外, 还有直线的方向, 也就是直线的倾斜程度.
1.倾斜角的定义
当直线l与x轴相交时,我们取x轴为基准,x轴的正方向与直线l向上方向之间所成的角α叫做直线l的倾斜角.
规定:当直线l与x轴平行或重合时,它的倾斜角为0°.
2.倾斜角的范围
平面内的任意一条直线都有确定的倾斜角α,其取值范围为:α∈[0,π)。
探究新知:一、直线的倾斜角
x
y
O
l1
l2
α
β
x
y
O
l3
基础练习
√
×
×
问题二:在平面直角坐标系中,设直线l的倾斜角为α.
(1) 已知直线l经过O(0, 0), P( , 1), α与O, P的坐标有什么关系
(2) 类似地,如果直线l经过P1(-1, 1), P2( , 0), α与P1, P2的坐标又有什么关系
(3) 一般地,如果直线l经过两点P1(x1, y1), P2(x2, y2), x1≠x2, 那么α与P1, P2的坐标有怎样的关系
探究二:直线的斜率
O
y
x
α
O
y
x
α
α
O
y
x
α
α
1.直线斜率的定义
我们把一条直线的的倾斜角α的正切值叫做这条直线的斜率(slope).斜率通常用小写字母k 表示,即:
k =tanα
注:倾斜角是90 °的直线没有斜率。
探究新知:二、直线的斜率
2.直线斜率的公式
综上所述,我们得到经过两点P1(x1,y1),P2(x2,y2)(x1≠x2)的直线斜率公式:
探究新知:二、直线的斜率
思考1:上述公式与P1,P2两点的顺序有关吗?
无关。
思考2:当直线P1P2与x轴平行或重合时,公式还成立吗?
成立。
思考3:当直线P1P2与y轴平行或重合时,公式还成立吗?
不成立。
探究新知:二、直线的斜率
探究新知:二、直线的斜率
【补充】
倾斜角α 0° 30° 45° 60° 120° 135° 150°
斜率k
3.倾斜角与斜率的变化关系
思考讨论:直线的倾斜角增大时,斜率如何变化
α∈[0°,90°)时,倾斜角越大,斜率越大;
α∈(90°,180°)时,倾斜角越大,斜率越大.
【提示】斜率范围:(-∞,+∞)
探究新知:二、直线的斜率
0°<α< 90°
α= 90°
90°< α <180°
α= 0°
k=0
k >0
k不存在
k<0
4.方向向量与斜率的关系
令P1P2=(x2-x1,y2-y1)
=(x,y)
则tanα = = =
探究新知:二、直线的斜率
【例1】如图2.1-6,已知A(3, 2),B(-4, 1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
教材例题
下列说法中,正确的是 ( )
A. 直线的倾斜角为α,则此直线的斜率为tanα
B. 直线的斜率为tanα,则此直线的倾斜角为α
C. 若直线的倾斜角为α,则sinα>0
D. 任意直线都有倾斜角α,且α ≠ 90°时,斜率为tanα
基础练习
D
一、直线的倾斜角
当堂小结
二、、斜率、坐标、方向向量间的关系
三、知识梳理
当堂小结
【题型一】已知经过A(m,2), B(-m,2m-1)的直线的倾斜角为α, 且45°<α<135°, 试求实数m的取值范围.
解:
思维拓展
【题型二】已知M,N坐标分别是(2,-3),(-3,-2),直线L经过点P(1,1)且与线段MN相交,求直线L的斜率k的范围.
思维拓展
O
x
y
P(1,1)
M(2,-3)
N(-3,-2)
