对2015年高考复习中的代数问题的几点思考
文档属性
| 名称 | 对2015年高考复习中的代数问题的几点思考 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-03 00:00:00 | ||
图片预览








文档简介
课件110张PPT。陕西师大附中 张锦川
mrzhang35@163.com
对2015年高考复习中的代数问题
的几点思考
?一、对2015年高考复习的总体认识
二、近年来代数部分试题特点
三、高考试题分析及规律探索
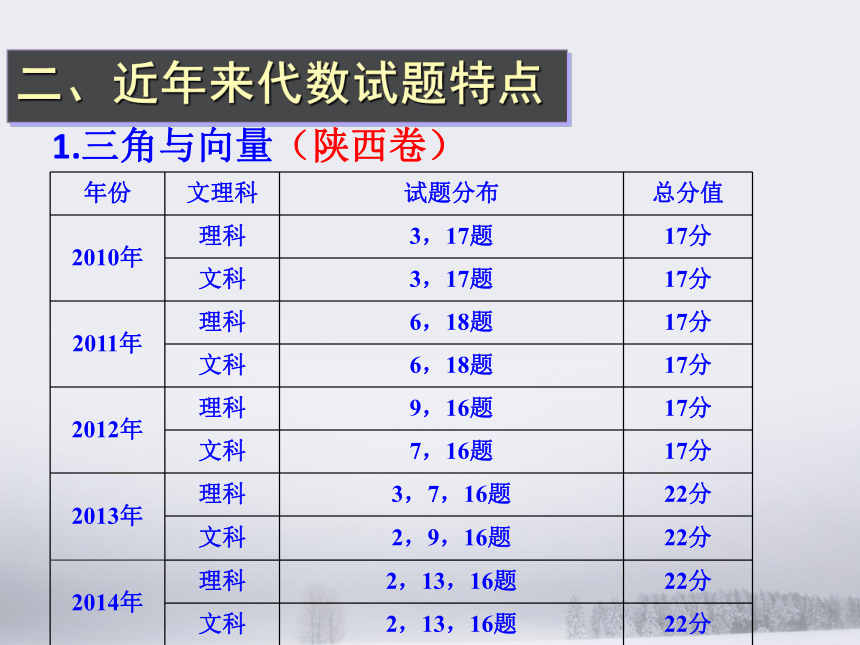
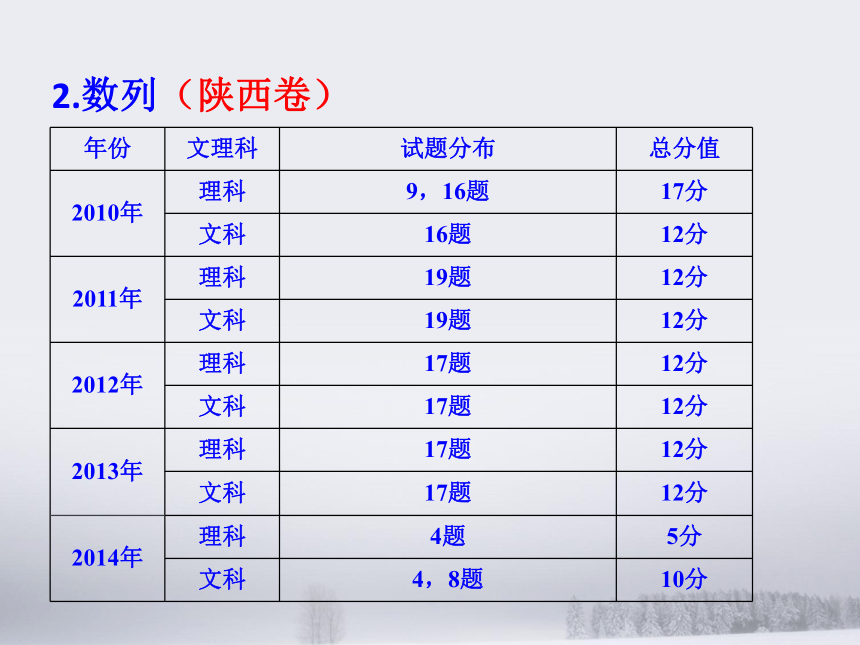
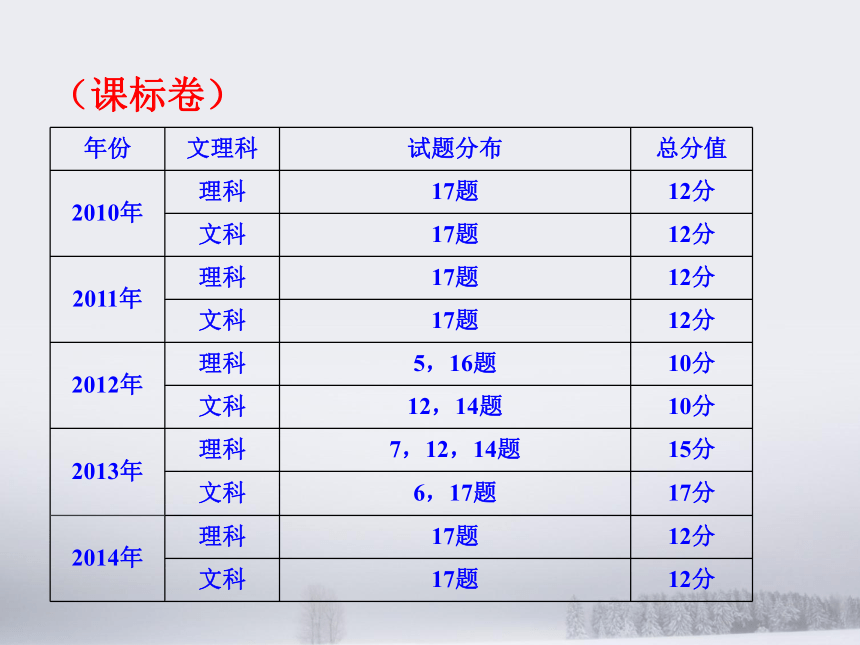
四、复习中的几点思考纲要: 自2006年陕西省高考数学自主命题以来,到今年刚好是第10年,自2010年进入新课标高考以来,到今年刚好是第6年.今年是陕西高考数学自主命题的最后一年,且要参照全国课标卷的命题框架.因此,我们既要立足于往年陕西卷的考查内容,考查重点,还要向全国课标卷的命题框架与难度靠拢.寻找差异,确定复习方向,以达到好的复习效果.一、对2015年高考复习的总体认识1.三角与向量(陕西卷)二、近年来代数试题特点(课标卷) 三角与向量在陕西卷中基本上稳定在两至三道试题,小题一至两道,大题一道,总分在17分至22分之间. 三角与向量在全国卷中有时出现三至四道小题,有时出现两道小题,一道大题,总分在15分至22分之间. 该部分内容考查三角函数的图像,三角恒等变形,解三角形,向量的基本概念,向量的夹角及模长,向量共线及垂直及向量的应用.难度不大.2.数列(陕西卷)(课标卷) 数列在陕西卷中基本上稳定在一至两道试题,小题最多一道,大题一道,总分在5分至17分之间. 数列在全国卷中有时出现两至三道小题,有时出现一道大题,总分在10分至17分之间. 该部分内容考查等差、等比数列,数列的通项公式,数列求和等内容,难度不大.
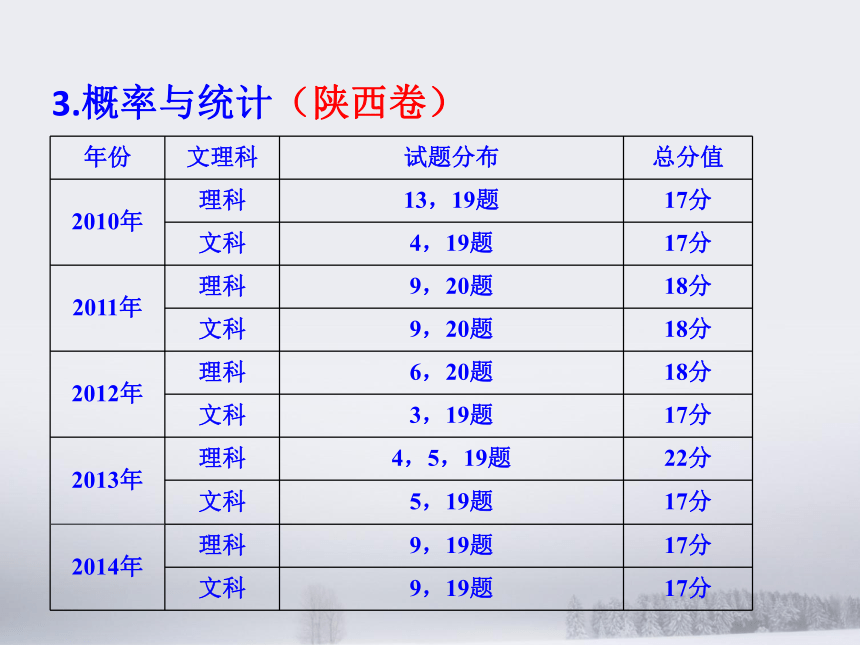
值得注意的是数列与算法框图,合情推理,充分必要条件,抽样方法等内容常常结合,这也是数列考题单独出现较少的一个原因.3.概率与统计(陕西卷)(课标卷)(此处2013,2014年为课标I卷) 概率与统计在陕西卷中基本上稳定在两道试题,一小一大,总分为17分. 数列在全国卷中也稳定在两道试题上,一小一大,总分为17分. 概率与统计部分考查抽样方法,样本中的数据特征,用样本估计总体的统计方法和思想,近年来回归方程和独立性检验也愈来愈受到重视.解答题往往以统计内容为切入点,在统计中设计概率问题,问题贴近生活,重视数学应用(文理要求有明显差异).4.函数与导数(陕西卷)(课标卷) 函数与导数在陕西卷中基本上稳定在三道至四道试题,小题两至三道,大题一道,总分在24分至29分之间. 函数与导数在全国卷中也稳定在三道至四道试题,小题两至三道,大题一道,总分在22分至27分之间. 这部分内容往往考查两个方面:1.基本初等函数的图像及性质;2.利用导数的方法研究函数的单调性、极值、最值,进而利用导数这一工具解决一些典型的数学问题. 在压轴题上,陕西卷往往一题三问,共14分;全国卷一题两问,12分.题目往往有一定的综合性和深刻的数学内涵.三、高考试题分析及规律探索板块1:三角与向量题型1:三角函数的图像和性质(三角恒等变形) 规律总结题型2:解三角形(应用题) 规律总结题型3:平面向量 规律总结板块2:数列题型1:等差数列与等比数列 规律总结题型2:数列的通项和求和 规律总结题型3:数列与不等式、函数的结合 规律总结题型3:数列与其他知识的结合 规律总结板块3:概率与统计题型1:抽样方法,统计图表及数字特征 规律总结题型2:古典概型 规律总结2011年陕西高考数学试题别解题型3:模拟方法(几何概型) 规律总结题型4:离散型随机变量的分布列、期望、方差 规律总结题型5:回归方程,独立性检验 规律总结板块4:函数与导数函
数
与
导
数基本初等函数(一)函数与导数函数与导数---构建体系基本
初等
函数
(一)函数的概念函数的性质二次函数幂、指、对函数的图像和性质函数与方程函数与导数---构建体系导
数导数的概念导数的运算导数的意义导数的应用物理意义几何意义函数与导数---构建体系导
数
的
应
用单调性极值与最值 与 图像间的关系定积分综合应用函数与导数---构建体系单
调
性证明或判断单调性求单调区间已知单调性求参数的值或取值范围函数与导数---构建体系极
值
与
最
值求极值求最值已知极值或最值求参数的值或取值范围函数与导数---构建体系综
合
应
用比较两实数的大小证明函数不等式函数不等式恒成立求参数的值或取值范围讨论方程的解的个数函数与导数---构建体系题型一:函数的概念与图像的应用题型二:函数性质的综合应用题型三:求导公式与求导法则的应用题型四:导数几何意义的应用题型五:利用导数研究函数的单调性题型六:利用导数研究函数的极值与最值题型七:利用导数研究方程的根(函数零点)题型八:利用导数证明函数不等式题型九:不等式恒成立求参数的值或取值范围函数与导数---明确题型题型1:函数的概念与图像的应用题型2:函数性质的综合应用题型3:求导公式与求导法则的应用题型4:导数几何意义的应用题型5:利用导数研究函数的单调性题型6:利用导数研究函数的极值与最值题型7:利用导数研究方程的根(函数零点)题型8:利用导数证明函数不等式题型9:不等式恒成立求参数的取值范围重视三大类解题方法二次函数分离参数构造函数函数与导数---掌握解法重视三大类解题技巧前为后用最小大于最大(复合最值)二次求导函数与导数---熟悉技巧四、复习中的几点思考1.研究考纲,分析试题 (1)把握知识的三个层次:了解(知道、模仿)、理解
(独立操作)、掌握(运用、迁移). (2)寻找考纲或者考试要求中有变化的部分,针对性地展开复习工作.不等式选讲2.发现问题,有效应对 (1)“三基”掌握不到位,认知结构不完善;
①基础知识不扎实,基本概念模糊不清;
②常用公式记忆不准确;
③基本技能和基本方法掌握不到位. (2)思维不严谨,解答不规范;
①思维不严谨,答题不规范;
②缺少主要解题过程. (3)能力不足,审题不清,会而不对,对而不全.
①运算能力差;
②算理不清,会而不对,对而不全.启示:
(1)重视表述,规范解题习惯;
(2)锻炼运算能力;
(3)养成画图习惯(画图可以帮助打开思路).3.回归教材,挖掘本质 新课程数学教材为了适应知识的螺旋上升的规律,同一知
识体系的内容会放在不同模块中去介绍.高三复习时应打破模
块顺序,按照学科内的知识体系,将分散在必修课程与选修课
程的同一知识体系的内容进行整合,建立条理化的知识结构.
特别要防止一些知识盲点的出现.例如,导数部分的内容经常
渗透函数与方程的思想,这一内容在必修一第四章学习过,在
复习中要有一个整体的函数眼光和思维.启示:
三抓:
(1)抓基本概念的准确和实质性的理解;
(2)抓公式、定理的熟练和初步应用;
(3)抓基本技能的正用、逆用、变用、连用、巧用.四过关:
(1)能准确理解书中的任一概念;
(2)能独立证明书中的每一定理;
(3)能熟练求解书中的所有例题;
(4)能历数书中各单元的作业类型.4.及时沟通,抓好落实(1)了解学生的真实状况
①学习状况;
②心理状况.
(2)抓好落实与反馈.
①抓好练习;
②抓好批改与反馈.
1.集合3.复数2.合情推理基础问题高频考点4.逻辑充要条件 含有一个量词的命题的否定四种命题 5.算法算法与分段函数综合 算法与数列求和、递推数列算法与统计结合(求样本的平均数、方差、标准差)基础问题高频考点6.平面向量向量共线与垂直 平面向量与三角函数的综合
平面向量与解析几何的综合向量的坐标表示 基础问题高频考点7.不等式基本不等式的应用 简单的线性规划一元二次不等式 基础问题高频考点8.(理科)排列组合与二项式定理排列与组合的应用 二项式定理(某一指定项、二项展开式的系数)基础问题高频考点9.三角函数三角函数的图像和性质(三角恒等变形) 解三角形(应用)基础问题高频考点10.数列等差、等比数列的基本运算 等差、等比数列的性质数列的函数属性数列求和(裂项相消、错位相减)累加法求通项基础问题高频考点11.立体几何三视图、面积与体积的计算 角的计算平行与垂直关系的判断与证明基础问题高频考点12.概率与统计统计图表 平均数、标准差、方差古典概型、互斥与独立事件的概率离散型随机变量的分布列、期望、方差几何概型(线性规划、定积分)基础问题高频考点13.解析几何直线与圆圆锥曲线的定义、标准方程、几何性质直线与椭圆、抛物线的位置关系(待定系数法求标准方程、最值、定值、定点、对称问题)基础问题高频考点14.函数与导数函数的概念(分段函数) 幂、指、对函数的图像和性质函数性质的综合应用函数与方程导数的应用(切线、单调性、极值与最值、函数不等式(参数范围、证明))基础问题高频考点15.选做题16.应用题线性规划 解三角形概率与统计17.创新题函数应用 数列应用 基础问题高频考点复杂问题题组设计2015届高三第一学期第2次模考试题研究2015届高三第一学期期中考试题研究2014年高考陕西卷理科压轴题的解法研究及赏析谢谢大家!
mrzhang35@163.com
对2015年高考复习中的代数问题
的几点思考
?一、对2015年高考复习的总体认识
二、近年来代数部分试题特点
三、高考试题分析及规律探索
四、复习中的几点思考纲要: 自2006年陕西省高考数学自主命题以来,到今年刚好是第10年,自2010年进入新课标高考以来,到今年刚好是第6年.今年是陕西高考数学自主命题的最后一年,且要参照全国课标卷的命题框架.因此,我们既要立足于往年陕西卷的考查内容,考查重点,还要向全国课标卷的命题框架与难度靠拢.寻找差异,确定复习方向,以达到好的复习效果.一、对2015年高考复习的总体认识1.三角与向量(陕西卷)二、近年来代数试题特点(课标卷) 三角与向量在陕西卷中基本上稳定在两至三道试题,小题一至两道,大题一道,总分在17分至22分之间. 三角与向量在全国卷中有时出现三至四道小题,有时出现两道小题,一道大题,总分在15分至22分之间. 该部分内容考查三角函数的图像,三角恒等变形,解三角形,向量的基本概念,向量的夹角及模长,向量共线及垂直及向量的应用.难度不大.2.数列(陕西卷)(课标卷) 数列在陕西卷中基本上稳定在一至两道试题,小题最多一道,大题一道,总分在5分至17分之间. 数列在全国卷中有时出现两至三道小题,有时出现一道大题,总分在10分至17分之间. 该部分内容考查等差、等比数列,数列的通项公式,数列求和等内容,难度不大.
值得注意的是数列与算法框图,合情推理,充分必要条件,抽样方法等内容常常结合,这也是数列考题单独出现较少的一个原因.3.概率与统计(陕西卷)(课标卷)(此处2013,2014年为课标I卷) 概率与统计在陕西卷中基本上稳定在两道试题,一小一大,总分为17分. 数列在全国卷中也稳定在两道试题上,一小一大,总分为17分. 概率与统计部分考查抽样方法,样本中的数据特征,用样本估计总体的统计方法和思想,近年来回归方程和独立性检验也愈来愈受到重视.解答题往往以统计内容为切入点,在统计中设计概率问题,问题贴近生活,重视数学应用(文理要求有明显差异).4.函数与导数(陕西卷)(课标卷) 函数与导数在陕西卷中基本上稳定在三道至四道试题,小题两至三道,大题一道,总分在24分至29分之间. 函数与导数在全国卷中也稳定在三道至四道试题,小题两至三道,大题一道,总分在22分至27分之间. 这部分内容往往考查两个方面:1.基本初等函数的图像及性质;2.利用导数的方法研究函数的单调性、极值、最值,进而利用导数这一工具解决一些典型的数学问题. 在压轴题上,陕西卷往往一题三问,共14分;全国卷一题两问,12分.题目往往有一定的综合性和深刻的数学内涵.三、高考试题分析及规律探索板块1:三角与向量题型1:三角函数的图像和性质(三角恒等变形) 规律总结题型2:解三角形(应用题) 规律总结题型3:平面向量 规律总结板块2:数列题型1:等差数列与等比数列 规律总结题型2:数列的通项和求和 规律总结题型3:数列与不等式、函数的结合 规律总结题型3:数列与其他知识的结合 规律总结板块3:概率与统计题型1:抽样方法,统计图表及数字特征 规律总结题型2:古典概型 规律总结2011年陕西高考数学试题别解题型3:模拟方法(几何概型) 规律总结题型4:离散型随机变量的分布列、期望、方差 规律总结题型5:回归方程,独立性检验 规律总结板块4:函数与导数函
数
与
导
数基本初等函数(一)函数与导数函数与导数---构建体系基本
初等
函数
(一)函数的概念函数的性质二次函数幂、指、对函数的图像和性质函数与方程函数与导数---构建体系导
数导数的概念导数的运算导数的意义导数的应用物理意义几何意义函数与导数---构建体系导
数
的
应
用单调性极值与最值 与 图像间的关系定积分综合应用函数与导数---构建体系单
调
性证明或判断单调性求单调区间已知单调性求参数的值或取值范围函数与导数---构建体系极
值
与
最
值求极值求最值已知极值或最值求参数的值或取值范围函数与导数---构建体系综
合
应
用比较两实数的大小证明函数不等式函数不等式恒成立求参数的值或取值范围讨论方程的解的个数函数与导数---构建体系题型一:函数的概念与图像的应用题型二:函数性质的综合应用题型三:求导公式与求导法则的应用题型四:导数几何意义的应用题型五:利用导数研究函数的单调性题型六:利用导数研究函数的极值与最值题型七:利用导数研究方程的根(函数零点)题型八:利用导数证明函数不等式题型九:不等式恒成立求参数的值或取值范围函数与导数---明确题型题型1:函数的概念与图像的应用题型2:函数性质的综合应用题型3:求导公式与求导法则的应用题型4:导数几何意义的应用题型5:利用导数研究函数的单调性题型6:利用导数研究函数的极值与最值题型7:利用导数研究方程的根(函数零点)题型8:利用导数证明函数不等式题型9:不等式恒成立求参数的取值范围重视三大类解题方法二次函数分离参数构造函数函数与导数---掌握解法重视三大类解题技巧前为后用最小大于最大(复合最值)二次求导函数与导数---熟悉技巧四、复习中的几点思考1.研究考纲,分析试题 (1)把握知识的三个层次:了解(知道、模仿)、理解
(独立操作)、掌握(运用、迁移). (2)寻找考纲或者考试要求中有变化的部分,针对性地展开复习工作.不等式选讲2.发现问题,有效应对 (1)“三基”掌握不到位,认知结构不完善;
①基础知识不扎实,基本概念模糊不清;
②常用公式记忆不准确;
③基本技能和基本方法掌握不到位. (2)思维不严谨,解答不规范;
①思维不严谨,答题不规范;
②缺少主要解题过程. (3)能力不足,审题不清,会而不对,对而不全.
①运算能力差;
②算理不清,会而不对,对而不全.启示:
(1)重视表述,规范解题习惯;
(2)锻炼运算能力;
(3)养成画图习惯(画图可以帮助打开思路).3.回归教材,挖掘本质 新课程数学教材为了适应知识的螺旋上升的规律,同一知
识体系的内容会放在不同模块中去介绍.高三复习时应打破模
块顺序,按照学科内的知识体系,将分散在必修课程与选修课
程的同一知识体系的内容进行整合,建立条理化的知识结构.
特别要防止一些知识盲点的出现.例如,导数部分的内容经常
渗透函数与方程的思想,这一内容在必修一第四章学习过,在
复习中要有一个整体的函数眼光和思维.启示:
三抓:
(1)抓基本概念的准确和实质性的理解;
(2)抓公式、定理的熟练和初步应用;
(3)抓基本技能的正用、逆用、变用、连用、巧用.四过关:
(1)能准确理解书中的任一概念;
(2)能独立证明书中的每一定理;
(3)能熟练求解书中的所有例题;
(4)能历数书中各单元的作业类型.4.及时沟通,抓好落实(1)了解学生的真实状况
①学习状况;
②心理状况.
(2)抓好落实与反馈.
①抓好练习;
②抓好批改与反馈.
1.集合3.复数2.合情推理基础问题高频考点4.逻辑充要条件 含有一个量词的命题的否定四种命题 5.算法算法与分段函数综合 算法与数列求和、递推数列算法与统计结合(求样本的平均数、方差、标准差)基础问题高频考点6.平面向量向量共线与垂直 平面向量与三角函数的综合
平面向量与解析几何的综合向量的坐标表示 基础问题高频考点7.不等式基本不等式的应用 简单的线性规划一元二次不等式 基础问题高频考点8.(理科)排列组合与二项式定理排列与组合的应用 二项式定理(某一指定项、二项展开式的系数)基础问题高频考点9.三角函数三角函数的图像和性质(三角恒等变形) 解三角形(应用)基础问题高频考点10.数列等差、等比数列的基本运算 等差、等比数列的性质数列的函数属性数列求和(裂项相消、错位相减)累加法求通项基础问题高频考点11.立体几何三视图、面积与体积的计算 角的计算平行与垂直关系的判断与证明基础问题高频考点12.概率与统计统计图表 平均数、标准差、方差古典概型、互斥与独立事件的概率离散型随机变量的分布列、期望、方差几何概型(线性规划、定积分)基础问题高频考点13.解析几何直线与圆圆锥曲线的定义、标准方程、几何性质直线与椭圆、抛物线的位置关系(待定系数法求标准方程、最值、定值、定点、对称问题)基础问题高频考点14.函数与导数函数的概念(分段函数) 幂、指、对函数的图像和性质函数性质的综合应用函数与方程导数的应用(切线、单调性、极值与最值、函数不等式(参数范围、证明))基础问题高频考点15.选做题16.应用题线性规划 解三角形概率与统计17.创新题函数应用 数列应用 基础问题高频考点复杂问题题组设计2015届高三第一学期第2次模考试题研究2015届高三第一学期期中考试题研究2014年高考陕西卷理科压轴题的解法研究及赏析谢谢大家!
同课章节目录
