北师大版数学九年级上册 4.7.1 相似三角形的性质 (1) 课件(共16张PPT)
文档属性
| 名称 | 北师大版数学九年级上册 4.7.1 相似三角形的性质 (1) 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 246.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-19 20:27:34 | ||
图片预览



文档简介
(共16张PPT)
4.7.1 相似三角形的性质(1)
第四章 相似的图形
1、什么是相似三角形
2、相似三角形的性质是什么?
回顾与反思
在两个相似三角形中是否只有对应角相等、对应边成比例这个性质呢?本节课我们将研究相似三角形的其他性质.
相似三角形的对应角相等,对应边成比例
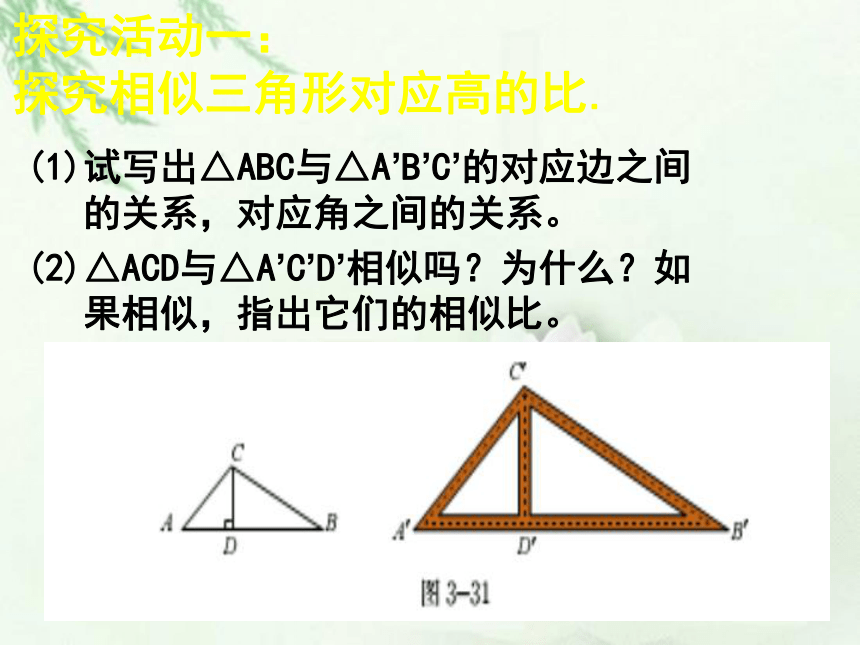
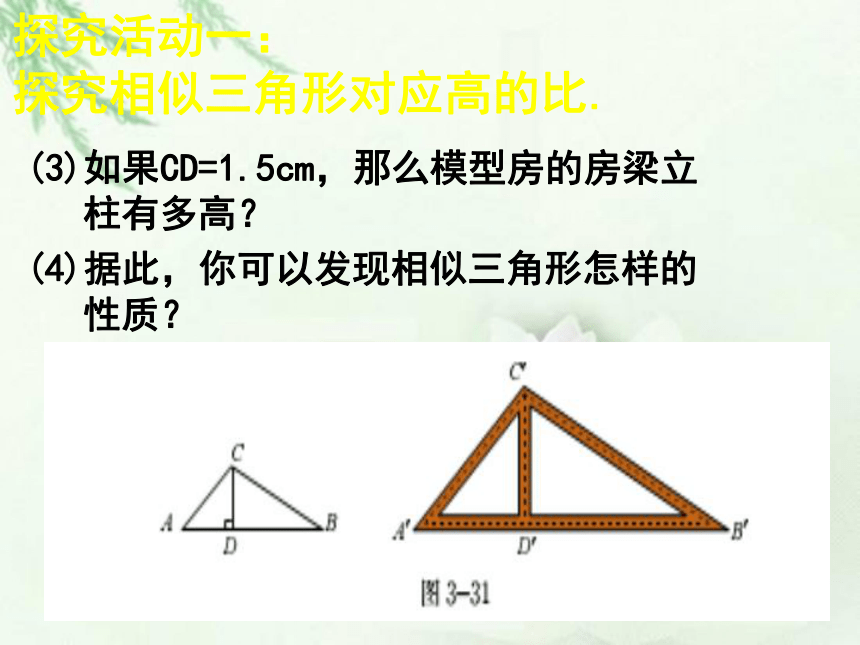
在生活中,我们经常利用相似的知识解决建筑类问题.如图,小王依据图纸上的△ABC,以1:2的比例建造了模型房梁△A’B’C’,CD和C’D’分别是它们的立柱。
探究活动一:
探究相似三角形对应高的比.
(1)试写出△ABC与△A’B’C’的对应边之间的关系,对应角之间的关系。
(2)△ACD与△A’C’D’相似吗?为什么?如果相似,指出它们的相似比。
探究活动一:
探究相似三角形对应高的比.
(3)如果CD=1.5cm,那么模型房的房梁立柱有多高?
(4)据此,你可以发现相似三角形怎样的性质?
探究活动一:
探究相似三角形对应高的比.
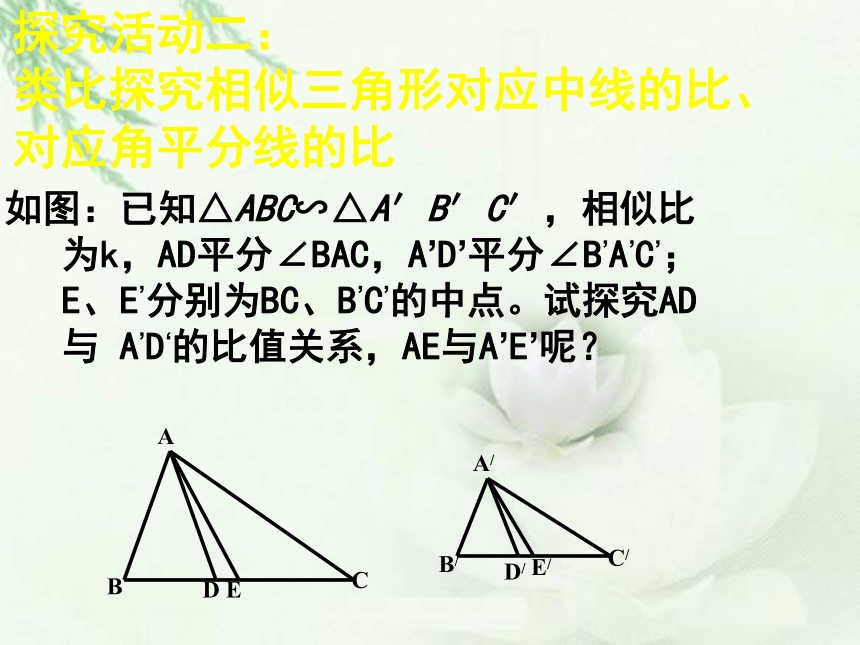
如图:已知△ABC∽△A′B′C′,相似比为k,AD平分∠BAC,A’D’平分∠B’A’C’;E、E’分别为BC、B’C’的中点。试探究AD与 A’D‘的比值关系,AE与A’E’呢?
探究活动二:
类比探究相似三角形对应中线的比、
对应角平分线的比
A
B
C
D
E
A/
B/
C/
D/
E/
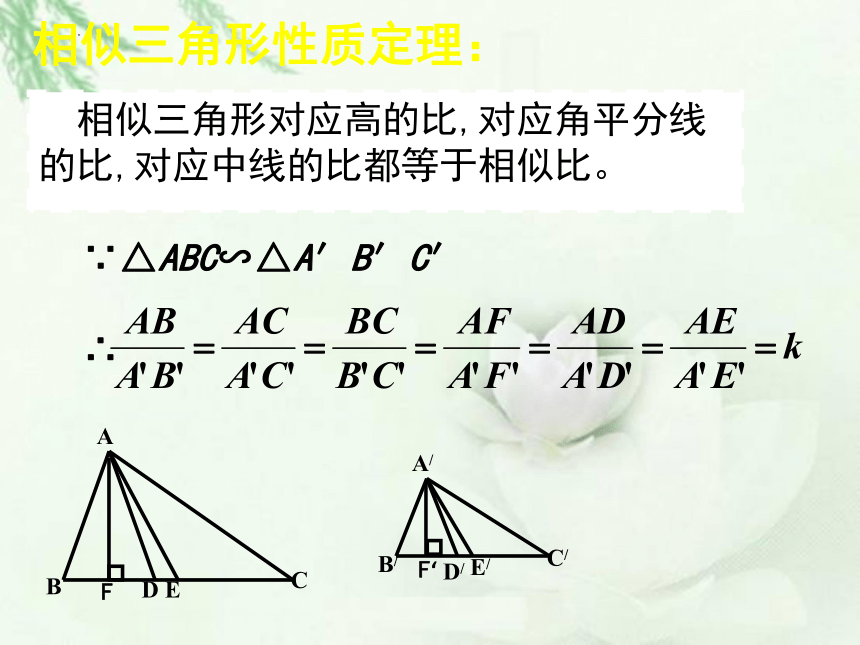
相似三角形性质定理:
相似三角形对应高的比,对应角平分线的比,对应中线的比都等于相似比。
∵△ABC∽△A′B′C′
∴
A
B
C
D
E
A/
B/
C/
D/
E/
F
F‘
变式拓展探究:
如果把角平分线、中线变为对应角的三等分线、四等分线、…n等分线,对应边的三等分线、四等分线、…n等分线,那么它们也具有特殊关系吗?
探究活动二:
类比探究相似三角形对应中线的比、
对应角平分线的比
探究活动二:(变式拓展)
探究活动二:(变式拓展)
(3)你能得到哪些结论?
相似三角形对应角的n等分线的比,对应边的n等分线的比都等于相似比。
三:学以致用
A
B
C
S
R
E
P
D
Q
(1)∵四边形PQRS是正方形
∴ RS∥BC
∴ ∠ASR=∠B,∠ARS=∠C
∴ △ASR∽△ABC.
(两角分别相等的两个三角形相似)
A
B
C
S
R
E
P
D
Q
三:学以致用
(2)∵ △ASR∽△ABC.
∴
设正方形PQRS的边长为xcm,
则AE=(40-x)cm,
解得,x=24.
所以正方形PQRS的边长为24cm.
(相似三角形对应高的比等于相似比)
A
B
C
S
R
E
P
D
Q
三:学以致用
三:学以致用
练习:(课本95页随堂练习2)
两个相似三角形中一组对应角平分线的长分别是2cm和5cm,求这两个三角形的相似比。在这两个三角形的一组对应中线中,如果较短的中线是3cm,那么较长的中线多长?
同学们:经历了这节课的探索学习,你在知识上和方法上什么收获呢?请说说看。
相似三角形的性质:
相似三角形对应高的比,对应角平分线的比,对应中线的比都等于相似比。
课堂小结
课本:
习题 1、2、3、4
五:布置作业
只要你能勇敢地不断地攀登,你就能更接近于知识的顶峰,祝愿善于探索、善于发现的你早日到达顶峰!
结束寄语
4.7.1 相似三角形的性质(1)
第四章 相似的图形
1、什么是相似三角形
2、相似三角形的性质是什么?
回顾与反思
在两个相似三角形中是否只有对应角相等、对应边成比例这个性质呢?本节课我们将研究相似三角形的其他性质.
相似三角形的对应角相等,对应边成比例
在生活中,我们经常利用相似的知识解决建筑类问题.如图,小王依据图纸上的△ABC,以1:2的比例建造了模型房梁△A’B’C’,CD和C’D’分别是它们的立柱。
探究活动一:
探究相似三角形对应高的比.
(1)试写出△ABC与△A’B’C’的对应边之间的关系,对应角之间的关系。
(2)△ACD与△A’C’D’相似吗?为什么?如果相似,指出它们的相似比。
探究活动一:
探究相似三角形对应高的比.
(3)如果CD=1.5cm,那么模型房的房梁立柱有多高?
(4)据此,你可以发现相似三角形怎样的性质?
探究活动一:
探究相似三角形对应高的比.
如图:已知△ABC∽△A′B′C′,相似比为k,AD平分∠BAC,A’D’平分∠B’A’C’;E、E’分别为BC、B’C’的中点。试探究AD与 A’D‘的比值关系,AE与A’E’呢?
探究活动二:
类比探究相似三角形对应中线的比、
对应角平分线的比
A
B
C
D
E
A/
B/
C/
D/
E/
相似三角形性质定理:
相似三角形对应高的比,对应角平分线的比,对应中线的比都等于相似比。
∵△ABC∽△A′B′C′
∴
A
B
C
D
E
A/
B/
C/
D/
E/
F
F‘
变式拓展探究:
如果把角平分线、中线变为对应角的三等分线、四等分线、…n等分线,对应边的三等分线、四等分线、…n等分线,那么它们也具有特殊关系吗?
探究活动二:
类比探究相似三角形对应中线的比、
对应角平分线的比
探究活动二:(变式拓展)
探究活动二:(变式拓展)
(3)你能得到哪些结论?
相似三角形对应角的n等分线的比,对应边的n等分线的比都等于相似比。
三:学以致用
A
B
C
S
R
E
P
D
Q
(1)∵四边形PQRS是正方形
∴ RS∥BC
∴ ∠ASR=∠B,∠ARS=∠C
∴ △ASR∽△ABC.
(两角分别相等的两个三角形相似)
A
B
C
S
R
E
P
D
Q
三:学以致用
(2)∵ △ASR∽△ABC.
∴
设正方形PQRS的边长为xcm,
则AE=(40-x)cm,
解得,x=24.
所以正方形PQRS的边长为24cm.
(相似三角形对应高的比等于相似比)
A
B
C
S
R
E
P
D
Q
三:学以致用
三:学以致用
练习:(课本95页随堂练习2)
两个相似三角形中一组对应角平分线的长分别是2cm和5cm,求这两个三角形的相似比。在这两个三角形的一组对应中线中,如果较短的中线是3cm,那么较长的中线多长?
同学们:经历了这节课的探索学习,你在知识上和方法上什么收获呢?请说说看。
相似三角形的性质:
相似三角形对应高的比,对应角平分线的比,对应中线的比都等于相似比。
课堂小结
课本:
习题 1、2、3、4
五:布置作业
只要你能勇敢地不断地攀登,你就能更接近于知识的顶峰,祝愿善于探索、善于发现的你早日到达顶峰!
结束寄语
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
