北师大版数学九年级上册 4.4.4 探索三角形相似的条件 (4)课件 (共16张PPT)
文档属性
| 名称 | 北师大版数学九年级上册 4.4.4 探索三角形相似的条件 (4)课件 (共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-19 20:33:00 | ||
图片预览




文档简介
(共16张PPT)
4.4.4 探索相似三角形的条件(4)
第四章 相似的图形
为什么翩翩起舞的芭蕾舞演员要掂起脚尖 为什么身材苗条的时装模特还要穿高跟鞋 为什么她们会给人感到和谐、平衡、舒适,美的感觉
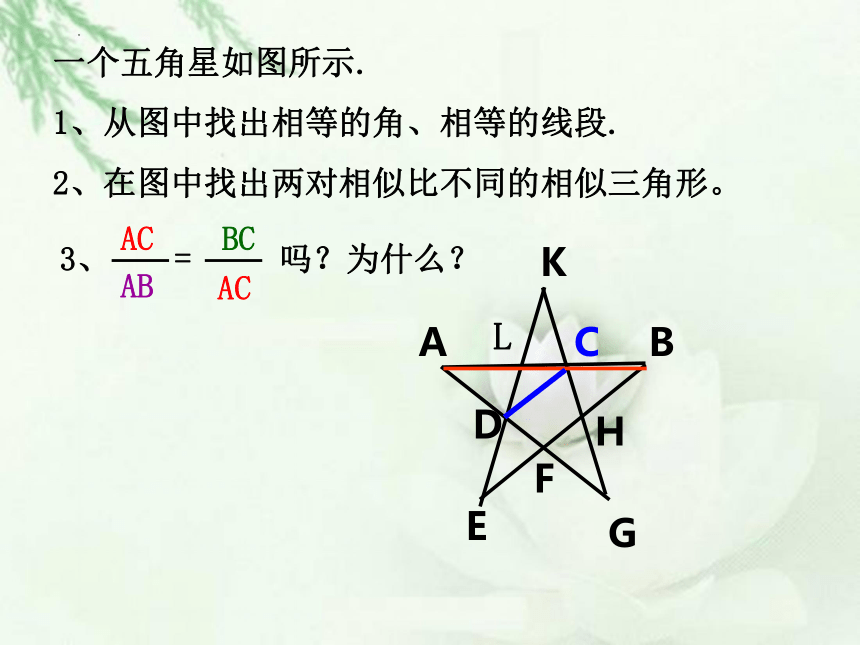
一个五角星如图所示.
1、从图中找出相等的角、相等的线段.
2、在图中找出两对相似比不同的相似三角形。
AC
AB
AC
BC
=
3、 吗?为什么?
A
C
B
D
K
E
G
F
H
L
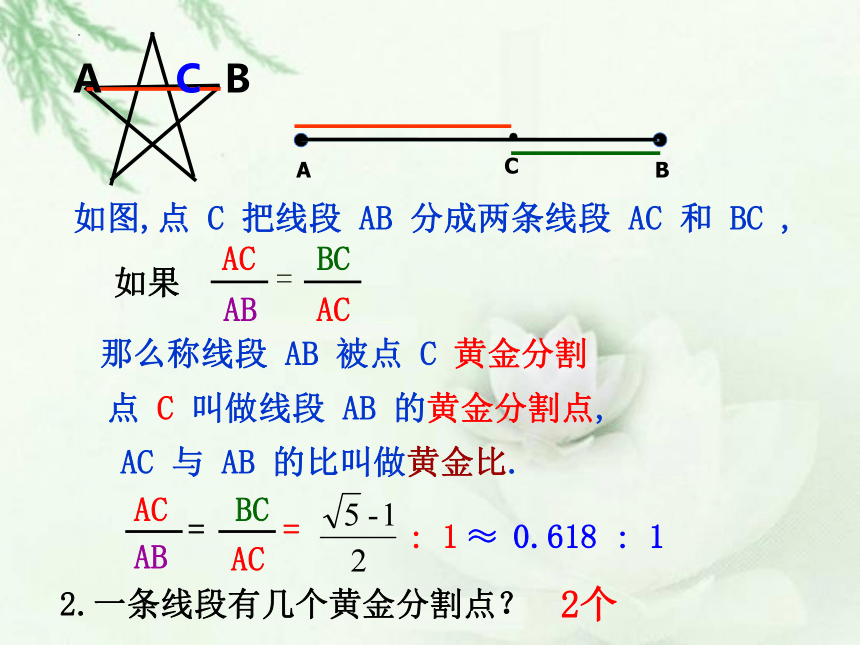
如图,点 C 把线段 AB 分成两条线段 AC 和 BC ,
如果
AC
AB
AC
BC
=
那么称线段 AB 被点 C 黄金分割
点 C 叫做线段 AB 的黄金分割点,
AC 与 AB 的比叫做黄金比.
C
A
B
A
C
B
: 1
≈
0.618 : 1
AC
AB
AC
BC
=
=
2个
2.一条线段有几个黄金分割点?
如图2-7,点C把线段AB分成两条线段AC和BC,如果 那么点C叫做线段AB的黄金分割点,AC与AB的比称为黄金比.
A
B
C
图2-7
由
得
则
∴
即
(舍去)
所以,黄金比
设
1
∴
x
例4 计算黄金比
解:
巴台农神庙
如果用图中的虚线表示的矩形画成如图所示的矩形ABCD,以矩形ABCD的宽为边在其内部作正方形AEFD,
那么我们可以惊奇的发现 ,点E是AB的
黄金分割点吗?矩形ABCD的宽与长的比是黄金比吗?
BC
BE
BC
AB
=
D
F
C
A
E
B
且BC=AE,
所以
因此点E是AB的黄金分割点,
矩形ABCD的宽与长的比是黄金比.
自己找出
黄金分割点
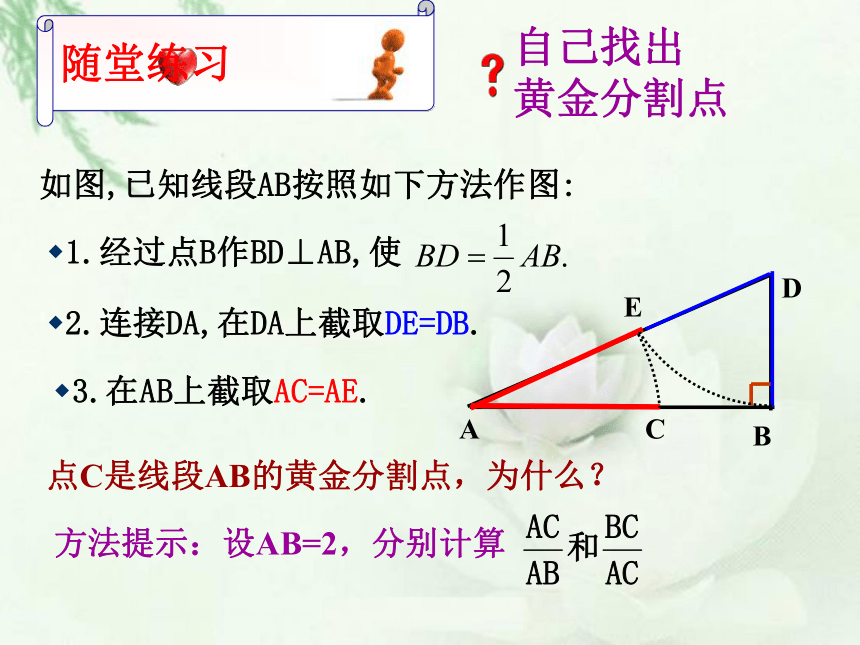
如图,已知线段AB按照如下方法作图:
1.经过点B作BD⊥AB,使
2.连接DA,在DA上截取DE=DB.
随堂练习
3.在AB上截取AC=AE.
A
B
D
E
C
点C是线段AB的黄金分割点,为什么?
方法提示:设AB=2,分别计算
如图,乐器上的一根弦AB=80cm,两个端点 A,B固定在乐器板面上,支撑点C是靠近点B的黄金分割点,点D是靠近点A的黄金分割点。试确定支撑点C到端点B的距离以及支撑点D到端点A的距离。
A
B
C
D
C
A
B
D
数学理解
当堂训练
1.设点C是长度为2cm的线段AB的黄金分割点,则AC的长为( )cm.
A. B.
C. D.
2.点P在线段AB上,且 ,若PB=1,则AB=( )
A. B. C. D.
3.电视台节目主持人在主持节目时,站在舞台的黄金分割点处最得体,若舞台AB的长为20m,试计算主持人应站在离A点为__________m处最佳
D
B
为什么翩翩起舞的芭蕾舞演员要掂起脚尖 为什么身材苗条的时装模特还要穿高跟鞋 为什么她们会给人感到和谐、平衡、舒适,美的感觉
黄金身材比例
人与黄金分割
人体肚脐不但是黄金点美化身型,有时还是医疗效果黄金点,许多民间名医在肚脐上贴药治好了某些疾病。人体最感舒适的温度是23℃(体温),也是正常人体温(37℃)的黄金点(23=37×0.618)。这说明医学与0.618有千丝万缕联系,尚待开拓研究。人体还有几个黄金点:肚脐上部分的黄金点在咽喉,肚脐以下部分的黄金点在膝盖,上肢的黄金点在肘关节。上肢与下肢长度之比均近似0.618.
4. 人体下半身(脚底到肚脐)的长度与身高的比例越接近0.618就越有美感,某女士身高160cm,下半身96cm,她应选择多高的高跟鞋会看起来更美呢?(精确到0.1厘米)
5.若一个矩形的宽与长之比等于黄金比,则称这个矩形为黄金矩形,试作出一个长为4cm的黄金矩形(保留作图痕迹)
A
B
解:设高跟鞋高x cm,则有
解得 x=7.5
所以应选择7.5cm高的高跟鞋
经检验x=7.5是原方程的根
1.作AB=4cm;
2.作AB的黄金分割点M(AM>BM);
作法:
3.作AD⊥AB,使AD=AM;
4.分别过B,D作AD和AB的平行线,两条平行
线相交于点C.
则四边形ABCD即为所作的黄金矩形.
M
D
C
A
B
5题 解:
异 曲 同 工
如图,设AB是已知线段,在AB上作正方形ABCD;取AD的中点E,连接EB;延长DA至F,使EF=EB;以线段AF为边作正方形AFGH。点H就是AB的黄金分割点。
如下方法也可以得到黄金分割点?
归 纳 小 结 :
1.通过建筑、雕塑、音乐等领域的实例了解黄金分割,感受了黄金分割的美。
2.进一步理解线段的比、成比例线段等相关内容。
3.通过作图找到一条线段的黄金分割点,并利用已学知识给予了说明。
谢 谢 大 家!
4.4.4 探索相似三角形的条件(4)
第四章 相似的图形
为什么翩翩起舞的芭蕾舞演员要掂起脚尖 为什么身材苗条的时装模特还要穿高跟鞋 为什么她们会给人感到和谐、平衡、舒适,美的感觉
一个五角星如图所示.
1、从图中找出相等的角、相等的线段.
2、在图中找出两对相似比不同的相似三角形。
AC
AB
AC
BC
=
3、 吗?为什么?
A
C
B
D
K
E
G
F
H
L
如图,点 C 把线段 AB 分成两条线段 AC 和 BC ,
如果
AC
AB
AC
BC
=
那么称线段 AB 被点 C 黄金分割
点 C 叫做线段 AB 的黄金分割点,
AC 与 AB 的比叫做黄金比.
C
A
B
A
C
B
: 1
≈
0.618 : 1
AC
AB
AC
BC
=
=
2个
2.一条线段有几个黄金分割点?
如图2-7,点C把线段AB分成两条线段AC和BC,如果 那么点C叫做线段AB的黄金分割点,AC与AB的比称为黄金比.
A
B
C
图2-7
由
得
则
∴
即
(舍去)
所以,黄金比
设
1
∴
x
例4 计算黄金比
解:
巴台农神庙
如果用图中的虚线表示的矩形画成如图所示的矩形ABCD,以矩形ABCD的宽为边在其内部作正方形AEFD,
那么我们可以惊奇的发现 ,点E是AB的
黄金分割点吗?矩形ABCD的宽与长的比是黄金比吗?
BC
BE
BC
AB
=
D
F
C
A
E
B
且BC=AE,
所以
因此点E是AB的黄金分割点,
矩形ABCD的宽与长的比是黄金比.
自己找出
黄金分割点
如图,已知线段AB按照如下方法作图:
1.经过点B作BD⊥AB,使
2.连接DA,在DA上截取DE=DB.
随堂练习
3.在AB上截取AC=AE.
A
B
D
E
C
点C是线段AB的黄金分割点,为什么?
方法提示:设AB=2,分别计算
如图,乐器上的一根弦AB=80cm,两个端点 A,B固定在乐器板面上,支撑点C是靠近点B的黄金分割点,点D是靠近点A的黄金分割点。试确定支撑点C到端点B的距离以及支撑点D到端点A的距离。
A
B
C
D
C
A
B
D
数学理解
当堂训练
1.设点C是长度为2cm的线段AB的黄金分割点,则AC的长为( )cm.
A. B.
C. D.
2.点P在线段AB上,且 ,若PB=1,则AB=( )
A. B. C. D.
3.电视台节目主持人在主持节目时,站在舞台的黄金分割点处最得体,若舞台AB的长为20m,试计算主持人应站在离A点为__________m处最佳
D
B
为什么翩翩起舞的芭蕾舞演员要掂起脚尖 为什么身材苗条的时装模特还要穿高跟鞋 为什么她们会给人感到和谐、平衡、舒适,美的感觉
黄金身材比例
人与黄金分割
人体肚脐不但是黄金点美化身型,有时还是医疗效果黄金点,许多民间名医在肚脐上贴药治好了某些疾病。人体最感舒适的温度是23℃(体温),也是正常人体温(37℃)的黄金点(23=37×0.618)。这说明医学与0.618有千丝万缕联系,尚待开拓研究。人体还有几个黄金点:肚脐上部分的黄金点在咽喉,肚脐以下部分的黄金点在膝盖,上肢的黄金点在肘关节。上肢与下肢长度之比均近似0.618.
4. 人体下半身(脚底到肚脐)的长度与身高的比例越接近0.618就越有美感,某女士身高160cm,下半身96cm,她应选择多高的高跟鞋会看起来更美呢?(精确到0.1厘米)
5.若一个矩形的宽与长之比等于黄金比,则称这个矩形为黄金矩形,试作出一个长为4cm的黄金矩形(保留作图痕迹)
A
B
解:设高跟鞋高x cm,则有
解得 x=7.5
所以应选择7.5cm高的高跟鞋
经检验x=7.5是原方程的根
1.作AB=4cm;
2.作AB的黄金分割点M(AM>BM);
作法:
3.作AD⊥AB,使AD=AM;
4.分别过B,D作AD和AB的平行线,两条平行
线相交于点C.
则四边形ABCD即为所作的黄金矩形.
M
D
C
A
B
5题 解:
异 曲 同 工
如图,设AB是已知线段,在AB上作正方形ABCD;取AD的中点E,连接EB;延长DA至F,使EF=EB;以线段AF为边作正方形AFGH。点H就是AB的黄金分割点。
如下方法也可以得到黄金分割点?
归 纳 小 结 :
1.通过建筑、雕塑、音乐等领域的实例了解黄金分割,感受了黄金分割的美。
2.进一步理解线段的比、成比例线段等相关内容。
3.通过作图找到一条线段的黄金分割点,并利用已学知识给予了说明。
谢 谢 大 家!
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
