人教版九年级数学上册 第23章 旋转 精讲精练 课件 (共36张PPT)
文档属性
| 名称 | 人教版九年级数学上册 第23章 旋转 精讲精练 课件 (共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 365.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-19 00:00:00 | ||
图片预览







文档简介
(共36张PPT)
课题
旋转专题
导入
1. 旋转:
旋转中心
A
P
P′
旋转角
B
O
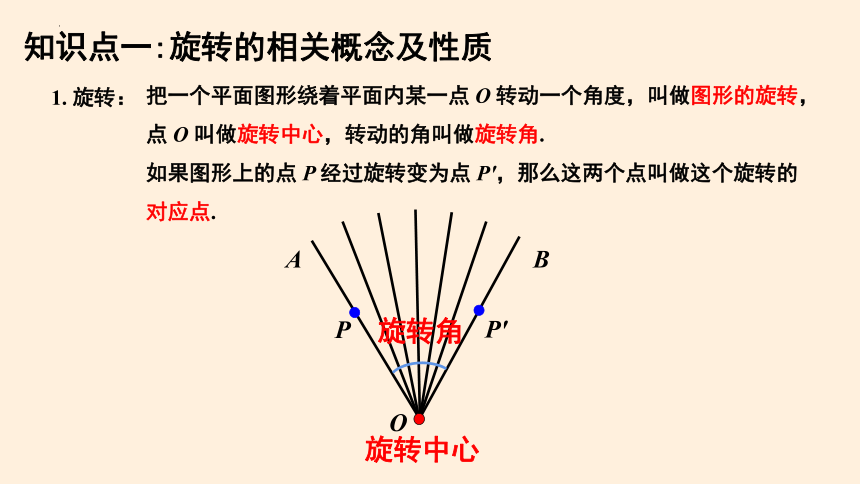
把一个平面图形绕着平面内某一点 O 转动一个角度,叫做图形的旋转, 点 O 叫做旋转中心,转动的角叫做旋转角.
如果图形上的点 P 经过旋转变为点 P′,那么这两个点叫做这个旋转的对应点.
知识点一:旋转的相关概念及性质
2. 旋转的三要素:旋转中心、旋转方向和旋转角.
在旋转过程中,始终保持不动的点是旋转中心,旋转中心可以在图形的内部,也可以在图形的外部,还可以是图形上的某点. 旋转方向有顺时针和逆时针两种.
3. 对应元素:一个图形绕旋转中心旋转一定角度后得到旋转后的图形.
如图:△ABC绕点O逆时针旋转90°得到△A′B′C′,
在这一旋转中,点O是旋转中心,
∠AOA′,∠BOB′,∠COC′都是旋转角,
点 A,B,C 分别与点 A′,B′,C′ 是对应点,
∠ABC,∠ACB,∠BAC分别与
∠A′B′C′,∠A′C′B′,∠B′A′C′是对应角,
线段AB,BC,CA分别与线段A′B′,B′C′,C′A′是对应边.
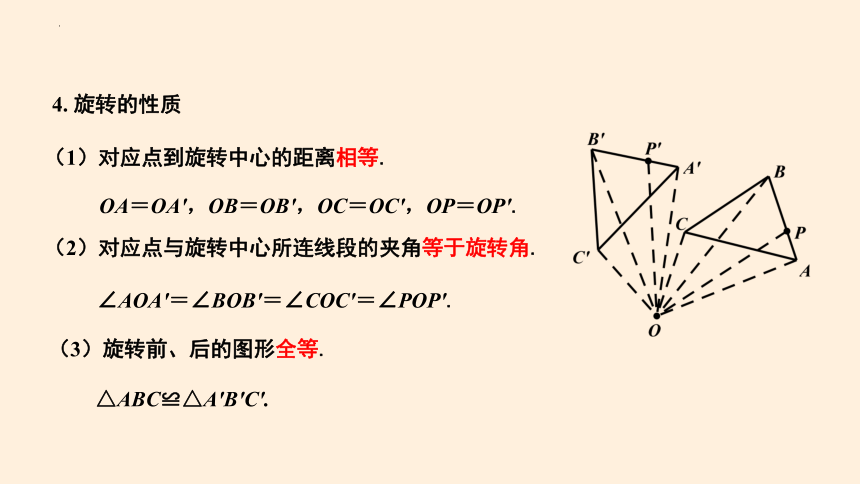
4. 旋转的性质
(1)对应点到旋转中心的距离相等.
OA=OA′,OB=OB′,OC=OC′,OP=OP′.
(2)对应点与旋转中心所连线段的夹角等于旋转角.
∠AOA′=∠BOB′=∠COC′=∠POP′.
(3)旋转前、后的图形全等.
△ABC≌△A′B′C′.
5. 旋转中心的确定
根据旋转的性质可知,对应点到旋转中心的距离相等,所以旋转中心位于对应点连线的垂直平分线上,即旋转中心是两对对应点所连线段的垂直平分线的交点.
例1
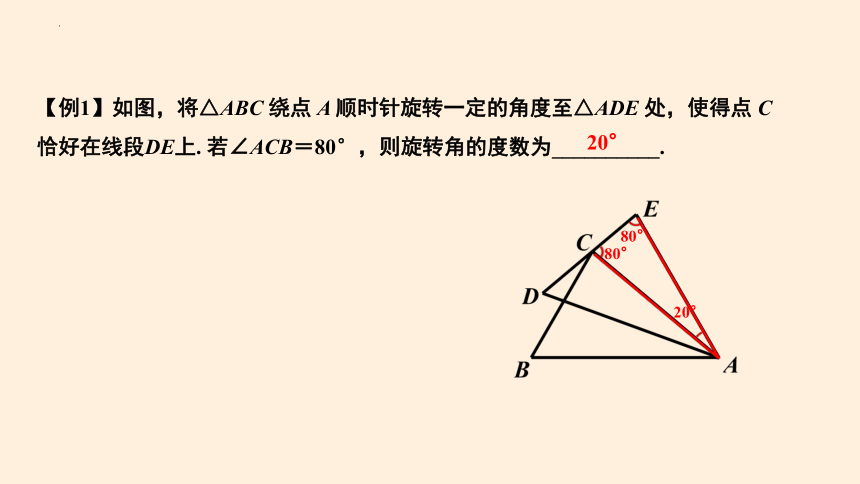
【例1】如图,将△ABC 绕点 A 顺时针旋转一定的角度至△ADE 处,使得点 C 恰好在线段DE上. 若∠ACB=80°,则旋转角的度数为__________.
80°
80°
20°
20°
巩固1
【巩固】
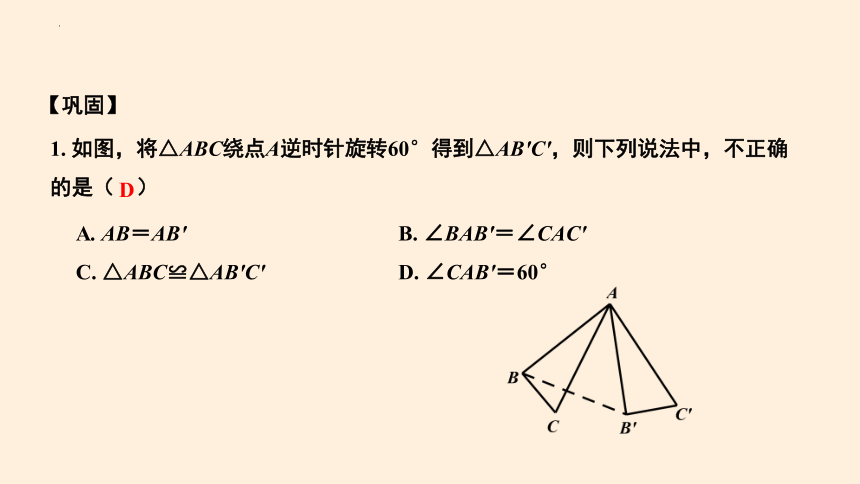
1. 如图,将△ABC绕点A逆时针旋转60°得到△AB′C′,则下列说法中,不正确的是( )
A. AB=AB′ B. ∠BAB′=∠CAC′
C. △ABC≌△AB′C′ D. ∠CAB′=60°
D
巩固2
2. 如图,在△ABC中,AB=4,AC=3,∠BAC=30°,将△ABC绕点 A 逆时针旋转60°得到△AB1C1,连接 BC1,则 BC1 的长为____________.
【巩固】
5
1. 作图依据
旋转的性质,即对应点到旋转中心的距离相等,每组对应点都旋转相同的角度.
2. 旋转作图的一般步骤
(1)确定旋转中心、旋转方向和旋转角.
(2)找出图形的关键点,一般是图形中的转折点.
(3)作旋转后的对应点: ①连;②转;③截.
(4)按原图形的顺序连接这些对应点,所得到的图形就是旋转后的图形.
(5)写出结论,说明作出的图形即为所求作的图形.
知识点二: 旋转作图
例2
【例2】如图.(1)请画出△ABC关于x轴的对称图形△A1B1C1,并写出点A1的坐标;
(2)请画出将△ABC绕点B逆时针旋转90°后得到的△A2BC2.
解:(1)如图所示,△A1B1C1即为所求,
点A1的坐标为(2,-4);
(2)如图所示,△A2B2C2即为所求.
巩固1
【巩固】
1. 如图,在平面直角坐标系中,点 A,C 在 x 轴上,点 C 的坐标为(-1,0),AC=2,将Rt△ABC先绕点 C 顺时针旋转 90°,再向右平移 3 个单位长度,则变换后点 A 的对应点的坐标是( )
A. (2,2) B. (1,2)
C. (-1,2) D. (2,-1)
A
巩固2
2. 如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
(1)将△ABC向下平移5个单位后得到△A1B1C1,
请画出△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,
请画出△A2B2C2.
【巩固】
知识点三
解:(1)如图所示,△A1B1C1即为所求;
(2)如图所示,△A2B2C2即为所求.
1. 中心对称的定义
把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心. 这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点.
知识点三:中心对称
2. 中心对称的性质
(1)中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分.
(2)中心对称的两个图形是全等图形.
3. 确定对称中心的方法
方法一:连接任意一对对称点,取这条线段的中点,则该点就是对称中心.
方法二:连接任意两对对称点,这两条线段的交点就是对称中心.
例3
【例 3】已知△ABC和△DEF关于点 O 对称,相应的对称点如图所示,则下列结论正确的是( )
A. AO=BO
B. BO=EO
C. 点A关于点O的对称点是点D
D. 点D在BO的延长线上
中心对称的两个图形,对称点所连线段都经过对称中心,
而且被对称中心所平分.
×
√
×
×
D
巩固1
【巩固】
1. 下列图形中,△A′B′C′与△ABC成中心对称的是( )
A. B.
C. D.
A
巩固2
【巩固】
2. 如图,△ABC与△DEF成中心对称,则下列关于对称中心的描述不正确的是( )
A. 对称中心是线段BE的中点 B. 对称中心是线段FC的中点
C. 对称中心是点C
D. 对称中心是线段AD与BE的交点
C
1. 中心对称图形
把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
知识点四:中心对称图形
2. 中心对称图形的性质
(1)中心对称图形上对称点的连线必经过对称中心,且被对称中心平分. 即过对称中心的直线与中心对称图形所交的两个对应交点是对称点.
(2)过对称中心的直线把中心对称图形分成全等的两部分(即周长和面积分别相等).
例4
【例4】下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
既是轴对称图形,又是中心对称图形
是中心对称图形,不是轴对称图形
是轴对称图形,
不是中心对称图形
是轴对称图形,
不是中心对称图形
A
巩固1
【巩固】
1. 下列图形:①平行四边形;②抛物线;③等边三角形;④矩形;⑤圆. 其中是中心对称图形的个数为( )
A. 1 B. 2 C. 3 D. 4
C
巩固2
2. 下列图形中是中心对称图形的是( )
【巩固】
A. B. C. D.
C
两个点关于原点对称时,它们的横、纵坐标分别互为相反数,
即点P(x,y)关于原点的对称点为P′(-x,-y).
关于原点对称的点的坐标
知识点五:关于原点对称的点的坐标
例5
【例5】已知 A(x,y-4)与点 B(1-y,2x)关于原点对称,求 的值.
点A与点B的横、纵坐标分别互为相反数
解:∵点A(x,y-4)与点B(1-y,2x)关于原点对称,
∴ ,
解得 ,
∴yx=21=2.
巩固1
【巩固】
1. 点 P(-2019,2020)关于原点的对称点 P′ 在( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
D
巩固2
2. 在平面直角坐标系中,已知点 P 关于 x 轴的对称点 P1 的坐标是(-5,6),则点 P 关于原点的对称点 P2 的坐标是____________.
【巩固】
(5,6)
巩固3
【巩固】
3. 如图所示,每个小正方形的边长为1个单位长度,作出△ABC关于原点对称的图形△A1B1C1,并写出A1,B1,C1的坐标.
解:如图所示,△A1B1C1即为所求;
A1,B1,C1的坐标为A1(2,-2),B1(3,0),C1(1,1).
课堂总结
课堂总结
1. 旋转的相关概念及性质
(1)旋转的三要素:旋转中心、旋转方向和旋转角.
(2)旋转的性质:①对应点到旋转中心的距离相等;②对应点与旋转中心所连线段的夹角等于旋转角;③旋转前、后的图形全等.
(3)旋转中心的确定:旋转中心是两对对应点所连线段的垂直平分线的交点.
2. 旋转作图
课堂总结
旋转作图的一般步骤
3. 中心对称
(1)中心对称的性质
①中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分.
②中心对称的两个图形是全等图形.
(2)确定对称中心的方法
课堂总结
方法一:连接任意一对对称点,取这条线段的中点,则该点就是对称中心.
方法二:连接任意两对对称点,这两条线段的交点就是对称中心.
课堂总结
4. 中心对称图形
中心对称图形的性质
(1)中心对称图形上对称点的连线必经过对称中心,且被对称中心平分. 即过对称中心的直线与中心对称图形所交的两个对应交点是对称点.
(2)过对称中心的直线把中心对称图形分成全等的两部分(即周长和面积分别相等).
5. 关于原点对称的点的坐标
课堂总结
两个点关于原点对称时,它们的横、纵坐标分别互为相反数,
即点P(x,y)关于原点的对称点为P′(-x,-y).
课题
旋转专题
导入
1. 旋转:
旋转中心
A
P
P′
旋转角
B
O
把一个平面图形绕着平面内某一点 O 转动一个角度,叫做图形的旋转, 点 O 叫做旋转中心,转动的角叫做旋转角.
如果图形上的点 P 经过旋转变为点 P′,那么这两个点叫做这个旋转的对应点.
知识点一:旋转的相关概念及性质
2. 旋转的三要素:旋转中心、旋转方向和旋转角.
在旋转过程中,始终保持不动的点是旋转中心,旋转中心可以在图形的内部,也可以在图形的外部,还可以是图形上的某点. 旋转方向有顺时针和逆时针两种.
3. 对应元素:一个图形绕旋转中心旋转一定角度后得到旋转后的图形.
如图:△ABC绕点O逆时针旋转90°得到△A′B′C′,
在这一旋转中,点O是旋转中心,
∠AOA′,∠BOB′,∠COC′都是旋转角,
点 A,B,C 分别与点 A′,B′,C′ 是对应点,
∠ABC,∠ACB,∠BAC分别与
∠A′B′C′,∠A′C′B′,∠B′A′C′是对应角,
线段AB,BC,CA分别与线段A′B′,B′C′,C′A′是对应边.
4. 旋转的性质
(1)对应点到旋转中心的距离相等.
OA=OA′,OB=OB′,OC=OC′,OP=OP′.
(2)对应点与旋转中心所连线段的夹角等于旋转角.
∠AOA′=∠BOB′=∠COC′=∠POP′.
(3)旋转前、后的图形全等.
△ABC≌△A′B′C′.
5. 旋转中心的确定
根据旋转的性质可知,对应点到旋转中心的距离相等,所以旋转中心位于对应点连线的垂直平分线上,即旋转中心是两对对应点所连线段的垂直平分线的交点.
例1
【例1】如图,将△ABC 绕点 A 顺时针旋转一定的角度至△ADE 处,使得点 C 恰好在线段DE上. 若∠ACB=80°,则旋转角的度数为__________.
80°
80°
20°
20°
巩固1
【巩固】
1. 如图,将△ABC绕点A逆时针旋转60°得到△AB′C′,则下列说法中,不正确的是( )
A. AB=AB′ B. ∠BAB′=∠CAC′
C. △ABC≌△AB′C′ D. ∠CAB′=60°
D
巩固2
2. 如图,在△ABC中,AB=4,AC=3,∠BAC=30°,将△ABC绕点 A 逆时针旋转60°得到△AB1C1,连接 BC1,则 BC1 的长为____________.
【巩固】
5
1. 作图依据
旋转的性质,即对应点到旋转中心的距离相等,每组对应点都旋转相同的角度.
2. 旋转作图的一般步骤
(1)确定旋转中心、旋转方向和旋转角.
(2)找出图形的关键点,一般是图形中的转折点.
(3)作旋转后的对应点: ①连;②转;③截.
(4)按原图形的顺序连接这些对应点,所得到的图形就是旋转后的图形.
(5)写出结论,说明作出的图形即为所求作的图形.
知识点二: 旋转作图
例2
【例2】如图.(1)请画出△ABC关于x轴的对称图形△A1B1C1,并写出点A1的坐标;
(2)请画出将△ABC绕点B逆时针旋转90°后得到的△A2BC2.
解:(1)如图所示,△A1B1C1即为所求,
点A1的坐标为(2,-4);
(2)如图所示,△A2B2C2即为所求.
巩固1
【巩固】
1. 如图,在平面直角坐标系中,点 A,C 在 x 轴上,点 C 的坐标为(-1,0),AC=2,将Rt△ABC先绕点 C 顺时针旋转 90°,再向右平移 3 个单位长度,则变换后点 A 的对应点的坐标是( )
A. (2,2) B. (1,2)
C. (-1,2) D. (2,-1)
A
巩固2
2. 如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
(1)将△ABC向下平移5个单位后得到△A1B1C1,
请画出△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,
请画出△A2B2C2.
【巩固】
知识点三
解:(1)如图所示,△A1B1C1即为所求;
(2)如图所示,△A2B2C2即为所求.
1. 中心对称的定义
把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心. 这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点.
知识点三:中心对称
2. 中心对称的性质
(1)中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分.
(2)中心对称的两个图形是全等图形.
3. 确定对称中心的方法
方法一:连接任意一对对称点,取这条线段的中点,则该点就是对称中心.
方法二:连接任意两对对称点,这两条线段的交点就是对称中心.
例3
【例 3】已知△ABC和△DEF关于点 O 对称,相应的对称点如图所示,则下列结论正确的是( )
A. AO=BO
B. BO=EO
C. 点A关于点O的对称点是点D
D. 点D在BO的延长线上
中心对称的两个图形,对称点所连线段都经过对称中心,
而且被对称中心所平分.
×
√
×
×
D
巩固1
【巩固】
1. 下列图形中,△A′B′C′与△ABC成中心对称的是( )
A. B.
C. D.
A
巩固2
【巩固】
2. 如图,△ABC与△DEF成中心对称,则下列关于对称中心的描述不正确的是( )
A. 对称中心是线段BE的中点 B. 对称中心是线段FC的中点
C. 对称中心是点C
D. 对称中心是线段AD与BE的交点
C
1. 中心对称图形
把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
知识点四:中心对称图形
2. 中心对称图形的性质
(1)中心对称图形上对称点的连线必经过对称中心,且被对称中心平分. 即过对称中心的直线与中心对称图形所交的两个对应交点是对称点.
(2)过对称中心的直线把中心对称图形分成全等的两部分(即周长和面积分别相等).
例4
【例4】下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
既是轴对称图形,又是中心对称图形
是中心对称图形,不是轴对称图形
是轴对称图形,
不是中心对称图形
是轴对称图形,
不是中心对称图形
A
巩固1
【巩固】
1. 下列图形:①平行四边形;②抛物线;③等边三角形;④矩形;⑤圆. 其中是中心对称图形的个数为( )
A. 1 B. 2 C. 3 D. 4
C
巩固2
2. 下列图形中是中心对称图形的是( )
【巩固】
A. B. C. D.
C
两个点关于原点对称时,它们的横、纵坐标分别互为相反数,
即点P(x,y)关于原点的对称点为P′(-x,-y).
关于原点对称的点的坐标
知识点五:关于原点对称的点的坐标
例5
【例5】已知 A(x,y-4)与点 B(1-y,2x)关于原点对称,求 的值.
点A与点B的横、纵坐标分别互为相反数
解:∵点A(x,y-4)与点B(1-y,2x)关于原点对称,
∴ ,
解得 ,
∴yx=21=2.
巩固1
【巩固】
1. 点 P(-2019,2020)关于原点的对称点 P′ 在( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
D
巩固2
2. 在平面直角坐标系中,已知点 P 关于 x 轴的对称点 P1 的坐标是(-5,6),则点 P 关于原点的对称点 P2 的坐标是____________.
【巩固】
(5,6)
巩固3
【巩固】
3. 如图所示,每个小正方形的边长为1个单位长度,作出△ABC关于原点对称的图形△A1B1C1,并写出A1,B1,C1的坐标.
解:如图所示,△A1B1C1即为所求;
A1,B1,C1的坐标为A1(2,-2),B1(3,0),C1(1,1).
课堂总结
课堂总结
1. 旋转的相关概念及性质
(1)旋转的三要素:旋转中心、旋转方向和旋转角.
(2)旋转的性质:①对应点到旋转中心的距离相等;②对应点与旋转中心所连线段的夹角等于旋转角;③旋转前、后的图形全等.
(3)旋转中心的确定:旋转中心是两对对应点所连线段的垂直平分线的交点.
2. 旋转作图
课堂总结
旋转作图的一般步骤
3. 中心对称
(1)中心对称的性质
①中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分.
②中心对称的两个图形是全等图形.
(2)确定对称中心的方法
课堂总结
方法一:连接任意一对对称点,取这条线段的中点,则该点就是对称中心.
方法二:连接任意两对对称点,这两条线段的交点就是对称中心.
课堂总结
4. 中心对称图形
中心对称图形的性质
(1)中心对称图形上对称点的连线必经过对称中心,且被对称中心平分. 即过对称中心的直线与中心对称图形所交的两个对应交点是对称点.
(2)过对称中心的直线把中心对称图形分成全等的两部分(即周长和面积分别相等).
5. 关于原点对称的点的坐标
课堂总结
两个点关于原点对称时,它们的横、纵坐标分别互为相反数,
即点P(x,y)关于原点的对称点为P′(-x,-y).
同课章节目录
