13.3.1等腰三角形的判定课件
文档属性
| 名称 | 13.3.1等腰三角形的判定课件 |  | |
| 格式 | zip | ||
| 文件大小 | 191.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-03 19:03:43 | ||
图片预览


文档简介
课件23张PPT。八年级数学 第十三章 轴对称等腰三角形的判定等腰三角形的两个底角有什么关系?等腰三角形的两底角相等.
(简写成 “ ”) ∵AC=AB(已知)
∴ ( )复习等边对等角反过来:如果∠B=∠C
那么AB=AC成立吗?大胆猜想:成立怎样进行验证?∠B=等边对等角∠C已知:D方法一:作BC边上的高AD方法二:作∠A的角平分线AD方法三:“作BC边上的中线AD”可行吗?在△ABC中,
∠B=∠C,求证:AB=AC 不行!这两个角所对的边也相等。已知等角对等边如果一个三角形有两个角相等,
那么 在△ABC中, ∵ ∠B=∠C ( ) ∴ AC= ( )AB那么这个三角形是等腰三角形简写成 “等角对等边”等腰三角形的性质与判定有区别吗?性质是:等边 等角判定是:等角 等边注意:使用这个两个定理的前提是-角和边要在同一个三角形中交换位置性质:等腰三角形的两底角相等.
(简写成 “等边对等角”) 判定: 有两角相等的三角形是等腰三角形
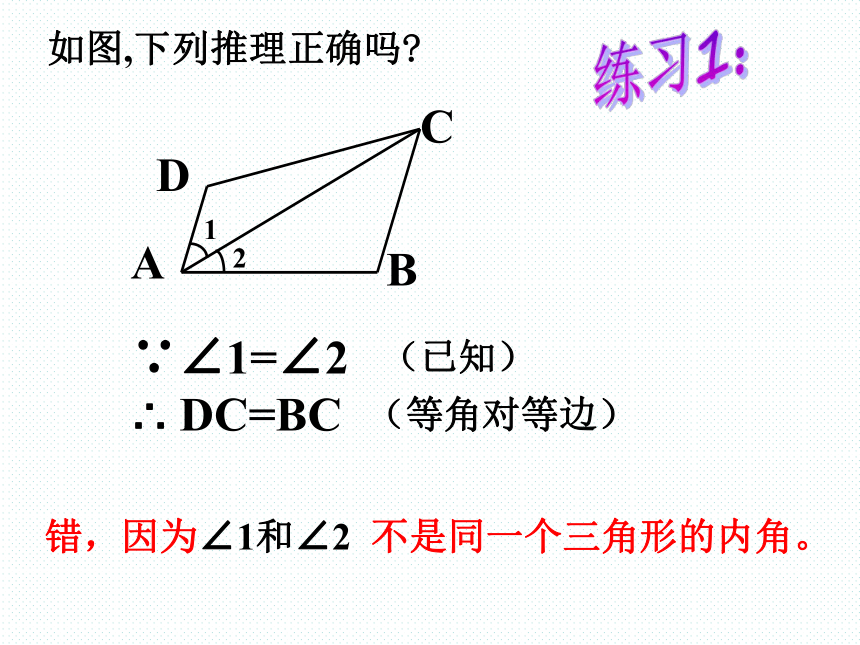
(简写成 “等角对等边”) 题设和结论 如图,下列推理正确吗? (等角对等边)错,因为∠1和∠2 不是同一个三角形的内角。练习1:(已知)例1:求证:如果三角形一个外角的平分线平行于
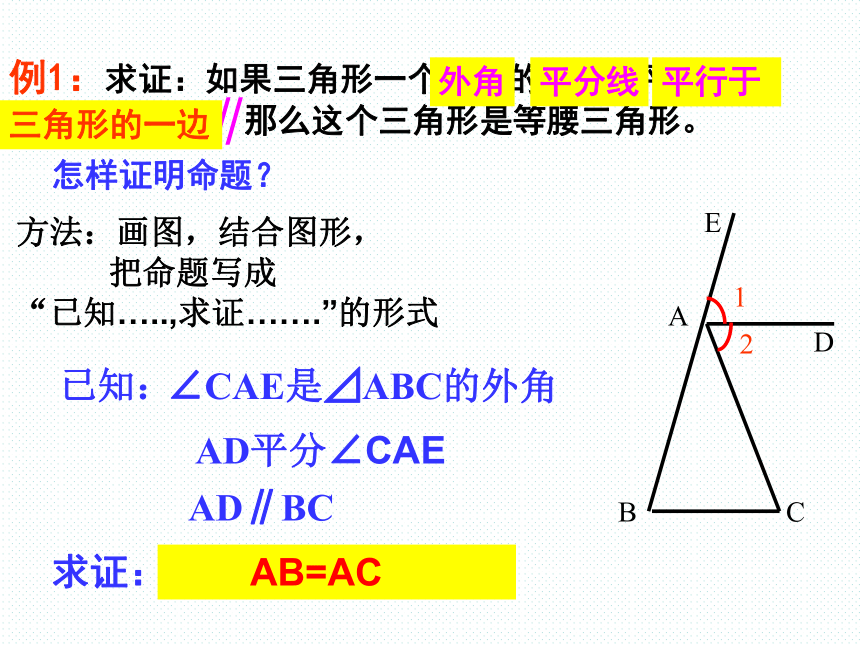
三角形的一边,那么这个三角形是等腰三角形。求证:∥外角平分线平行于已知:AD平分∠CAEAD∥BC∠CAE是⊿ABC的外角△ABC是等腰三角形怎样证明命题? AB=AC三角形的一边方法:画图,结合图形,
把命题写成
“已知…..,求证…….”的形式
例1 求证:如果三角形一个外角的平分线平行于
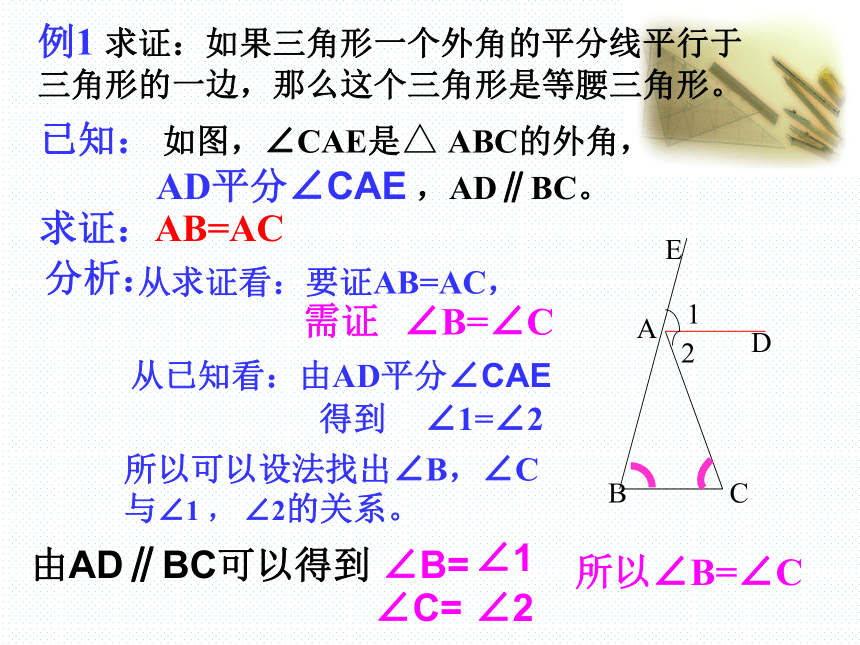
三角形的一边,那么这个三角形是等腰三角形。已知: 如图,∠CAE是△ ABC的外角, AD平分∠CAE ,AD∥BC。求证:AB=AC分析:从求证看:要证AB=AC,从已知看:由AD平分∠CAE 所以可以设法找出∠B,∠C与∠1 , ∠2的关系。∠B=∠C需证由AD∥BC可以得到∠B=∠1∠C=∠2所以∠B=∠C 得到 ∠1=∠2证明:∵AD∥BC∴∠1= ( )
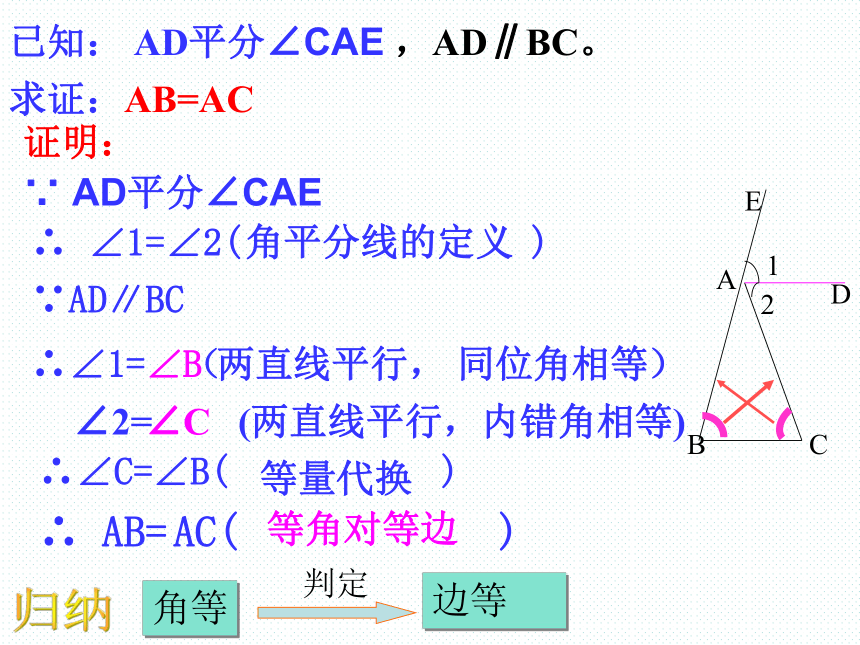
∴ ∠1=∠2( )∴∠C=∴ AB=两直线平行, 同位角相等(两直线平行,内错角相等)∠2= 等角对等边 归纳角等边等判定已知: AD平分∠CAE ,AD∥BC。∵ AD平分∠CAE求证:AB=AC角平分线的定义 等量代换 ∠B∠C∠B( )AC( ) 例题拓展
已知:∠CAE是△ABC的外角,
,且 AD∥BC.
求证: AD平分∠EAC AB=AC证明:
∵ AB=AC
∴ ∠B=∠C( )
∵ AD∥BC
∴ ∠1=∠B ( )
∠2=∠C ( )
∴∠1=∠2 ( )
即 AD平分∠CAE ( )等边对等角两直线平行, 同位角相等两直线平行,内错角相等 等量代换角平分线的定义如图,OA=OB, AB∥DC,
求证:OC=OD.分析: 练习2:(1)从求证看:
要证 OC=OD需证∠D=∠C(2)从已知看:
由OA=OB 得到∠B=∠A由AB∥DC得到∠D=∠B∠C=∠A所以:∠D=∠C∵OA=OB ∴∠A=∠B( )∵ AB∥DC ∴∠A= ∠B=
∴ ∠C=∠D ∴ OC=OD( ) 如图,OA=OB, AB∥DC,
求证:OC=OD.证明: ∠C∠D(两直线平行,内错角相等)归纳角等边等(等量代换)等角对等边等边对等角练习2:如图:
求证:练习2:OA=OB,OC=OD. AB∥DC,如图,OA=OB, AB∥DC,
求证:OC=OD.你能否设计一个变式题目?怎样设计? 变式一如图:
求证:练习2:OA=OB,OC=OD. AB∥DC,如图,OA=OB, AB∥DC,
求证:OC=OD.如图,OC=OD, AB∥DC,
求证:OA=OB 变式一 变式二例3 已知: BD平分∠ABC , AD∥BC 。
求证: AB=AD
证明:∵ BD平分∠ABC∴ ∠ 1 = ∠2( )角平分线的定义 ∵ AD∥BC∴ ∠ 1 = ∠3( ) 两直线平行,内错角相等 ∴ ∠ 2= ∠ 3( )等量代换 ∴ AB=AD( )等角对等边 (1)一个角的角平分线
(2)平行于角的一边的直线等腰三角形变式1:已知:BD平分∠ABC, AD ∥BC,
求证:AB=AD证明: ∵ BD平分∠ABC
∴ ∠1=∠2
∵ AD ∥BC
∴ ∠1=∠3
∴ ∠2=∠3
∴ AB=AD变式2 、已知:BD平分∠ABC, AD ∥BC,
求证:AB=ADE证明: ∵ BD平分∠ABC
∴ ∠1=∠2
∵ AD ∥BC
∴ ∠1=∠3
∴ ∠2=∠3
∴ AB=AD变式3: 在ΔABC中,OB平分∠ABC,
OC平分∠ACB,过O点作MN ∥BC.(1)图中有没有等腰三
角形?有几个?有两个等腰三角形ΔOBMΔOCN练习 在ΔABC中,OB平分∠ABC,
OC平分∠ACB,过O点作MN ∥BC.(1)图中有没有等腰三
角形?有几个?(2)线段BM、CN与MN
的长度有什么关系?有两个等腰三角形ΔOBMΔOCN∵ OM=BM ON=CN MN=∴ MN=OM+ONBM+CN练习 在ΔABC中,OB平分∠ABC,
OC平分∠ACB,过O点作MN ∥BC.(2)线段BM、CN与MN
的长度有什么关系?∴MN=(3) ΔAMN的周长=AB+AC吗?为什么?∵ ΔAMN的周长=AM+MN+AN=AM+=ABBM+CN+AN+AC等腰三角形的判定等腰三角形的判定方法等腰三角形性质与判定的区别两边相等的三角形两角相等
的三角形互为逆命题等腰三角形的判定定理是证明
线段相等的一种重要 的方法小结基本模型变式模型已知:⊿ABC中,∠B=∠C求证:AB=AC证明:经过点A作AD⊥BC,垂足为D.
在⊿ABD和⊿ACD中,∠B=∠C,
∠1=∠2
AD=AD∴ ⊿ABD≌ ⊿ACD( )∴AB=AC( )∴ ∠1= ∠2=90°21AAS全等三角形的对应边相等即:⊿ABC是等腰三角形⊿ABC等腰三角形已知:⊿ABC中,∠B=∠C求证:AB=AC:证明:作∠BAC的平分线AD在⊿ABD和⊿ACD中,∠B=∠C
∠1=∠2
AD=AD∴ ⊿ABD≌ ⊿ACD( )∴AB=AC( )12∴ ∠1=∠2AAS全等三角形的对应边相等
(简写成 “ ”) ∵AC=AB(已知)
∴ ( )复习等边对等角反过来:如果∠B=∠C
那么AB=AC成立吗?大胆猜想:成立怎样进行验证?∠B=等边对等角∠C已知:D方法一:作BC边上的高AD方法二:作∠A的角平分线AD方法三:“作BC边上的中线AD”可行吗?在△ABC中,
∠B=∠C,求证:AB=AC 不行!这两个角所对的边也相等。已知等角对等边如果一个三角形有两个角相等,
那么 在△ABC中, ∵ ∠B=∠C ( ) ∴ AC= ( )AB那么这个三角形是等腰三角形简写成 “等角对等边”等腰三角形的性质与判定有区别吗?性质是:等边 等角判定是:等角 等边注意:使用这个两个定理的前提是-角和边要在同一个三角形中交换位置性质:等腰三角形的两底角相等.
(简写成 “等边对等角”) 判定: 有两角相等的三角形是等腰三角形
(简写成 “等角对等边”) 题设和结论 如图,下列推理正确吗? (等角对等边)错,因为∠1和∠2 不是同一个三角形的内角。练习1:(已知)例1:求证:如果三角形一个外角的平分线平行于
三角形的一边,那么这个三角形是等腰三角形。求证:∥外角平分线平行于已知:AD平分∠CAEAD∥BC∠CAE是⊿ABC的外角△ABC是等腰三角形怎样证明命题? AB=AC三角形的一边方法:画图,结合图形,
把命题写成
“已知…..,求证…….”的形式
例1 求证:如果三角形一个外角的平分线平行于
三角形的一边,那么这个三角形是等腰三角形。已知: 如图,∠CAE是△ ABC的外角, AD平分∠CAE ,AD∥BC。求证:AB=AC分析:从求证看:要证AB=AC,从已知看:由AD平分∠CAE 所以可以设法找出∠B,∠C与∠1 , ∠2的关系。∠B=∠C需证由AD∥BC可以得到∠B=∠1∠C=∠2所以∠B=∠C 得到 ∠1=∠2证明:∵AD∥BC∴∠1= ( )
∴ ∠1=∠2( )∴∠C=∴ AB=两直线平行, 同位角相等(两直线平行,内错角相等)∠2= 等角对等边 归纳角等边等判定已知: AD平分∠CAE ,AD∥BC。∵ AD平分∠CAE求证:AB=AC角平分线的定义 等量代换 ∠B∠C∠B( )AC( ) 例题拓展
已知:∠CAE是△ABC的外角,
,且 AD∥BC.
求证: AD平分∠EAC AB=AC证明:
∵ AB=AC
∴ ∠B=∠C( )
∵ AD∥BC
∴ ∠1=∠B ( )
∠2=∠C ( )
∴∠1=∠2 ( )
即 AD平分∠CAE ( )等边对等角两直线平行, 同位角相等两直线平行,内错角相等 等量代换角平分线的定义如图,OA=OB, AB∥DC,
求证:OC=OD.分析: 练习2:(1)从求证看:
要证 OC=OD需证∠D=∠C(2)从已知看:
由OA=OB 得到∠B=∠A由AB∥DC得到∠D=∠B∠C=∠A所以:∠D=∠C∵OA=OB ∴∠A=∠B( )∵ AB∥DC ∴∠A= ∠B=
∴ ∠C=∠D ∴ OC=OD( ) 如图,OA=OB, AB∥DC,
求证:OC=OD.证明: ∠C∠D(两直线平行,内错角相等)归纳角等边等(等量代换)等角对等边等边对等角练习2:如图:
求证:练习2:OA=OB,OC=OD. AB∥DC,如图,OA=OB, AB∥DC,
求证:OC=OD.你能否设计一个变式题目?怎样设计? 变式一如图:
求证:练习2:OA=OB,OC=OD. AB∥DC,如图,OA=OB, AB∥DC,
求证:OC=OD.如图,OC=OD, AB∥DC,
求证:OA=OB 变式一 变式二例3 已知: BD平分∠ABC , AD∥BC 。
求证: AB=AD
证明:∵ BD平分∠ABC∴ ∠ 1 = ∠2( )角平分线的定义 ∵ AD∥BC∴ ∠ 1 = ∠3( ) 两直线平行,内错角相等 ∴ ∠ 2= ∠ 3( )等量代换 ∴ AB=AD( )等角对等边 (1)一个角的角平分线
(2)平行于角的一边的直线等腰三角形变式1:已知:BD平分∠ABC, AD ∥BC,
求证:AB=AD证明: ∵ BD平分∠ABC
∴ ∠1=∠2
∵ AD ∥BC
∴ ∠1=∠3
∴ ∠2=∠3
∴ AB=AD变式2 、已知:BD平分∠ABC, AD ∥BC,
求证:AB=ADE证明: ∵ BD平分∠ABC
∴ ∠1=∠2
∵ AD ∥BC
∴ ∠1=∠3
∴ ∠2=∠3
∴ AB=AD变式3: 在ΔABC中,OB平分∠ABC,
OC平分∠ACB,过O点作MN ∥BC.(1)图中有没有等腰三
角形?有几个?有两个等腰三角形ΔOBMΔOCN练习 在ΔABC中,OB平分∠ABC,
OC平分∠ACB,过O点作MN ∥BC.(1)图中有没有等腰三
角形?有几个?(2)线段BM、CN与MN
的长度有什么关系?有两个等腰三角形ΔOBMΔOCN∵ OM=BM ON=CN MN=∴ MN=OM+ONBM+CN练习 在ΔABC中,OB平分∠ABC,
OC平分∠ACB,过O点作MN ∥BC.(2)线段BM、CN与MN
的长度有什么关系?∴MN=(3) ΔAMN的周长=AB+AC吗?为什么?∵ ΔAMN的周长=AM+MN+AN=AM+=ABBM+CN+AN+AC等腰三角形的判定等腰三角形的判定方法等腰三角形性质与判定的区别两边相等的三角形两角相等
的三角形互为逆命题等腰三角形的判定定理是证明
线段相等的一种重要 的方法小结基本模型变式模型已知:⊿ABC中,∠B=∠C求证:AB=AC证明:经过点A作AD⊥BC,垂足为D.
在⊿ABD和⊿ACD中,∠B=∠C,
∠1=∠2
AD=AD∴ ⊿ABD≌ ⊿ACD( )∴AB=AC( )∴ ∠1= ∠2=90°21AAS全等三角形的对应边相等即:⊿ABC是等腰三角形⊿ABC等腰三角形已知:⊿ABC中,∠B=∠C求证:AB=AC:证明:作∠BAC的平分线AD在⊿ABD和⊿ACD中,∠B=∠C
∠1=∠2
AD=AD∴ ⊿ABD≌ ⊿ACD( )∴AB=AC( )12∴ ∠1=∠2AAS全等三角形的对应边相等
