北师大版数学九年级上册 1.3 正方形的性质判定(2)教学设计
文档属性
| 名称 | 北师大版数学九年级上册 1.3 正方形的性质判定(2)教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 299.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-20 10:05:39 | ||
图片预览

文档简介
1.3 正方形的性质与判定(2)
教学目标
探索并证明正方形的判定定理,进一步发展推理能力,
体会探索与证明过程中所蕴含的抽象、推理等数学思想
教学重点:探索并证明正方形的判定定理;
教学难点:综合应用菱形、矩形、正方形的性质定理和判定定理
教学过程
回顾与思考
问题1 什么样的四边形是正方形 正方形有哪些性质?.写下来
投影:1、定义:有一个角是直角且有一组邻边相等的平行四边形
2、性质 边:四边都相等,对边平行
角:四个角都是直角
对角线:相等、垂直且互相平分
对称性:中心对称、轴对称图形
(二) 新课探究
1、问题2 你认为怎样判定一个四边形是正方形?
如图所示,将一张长方形纸对折两次,然后剪下一个角,打开.怎样剪才能剪出一个正方形 动手做一做
(活动目的:通过活动,引入正方形的判定问题)
投影:
2、问题3 议一议:满足什么条件的菱形是正方形 满足什么条件的矩形是正方形 与同伴交流一下.写下来
(目的:引导学生讨论正方形的判定方法,形成判定正方形的基本思路:一个四边形既是矩形又是菱形,这个四边形就是正方形。)
3、例题讲解
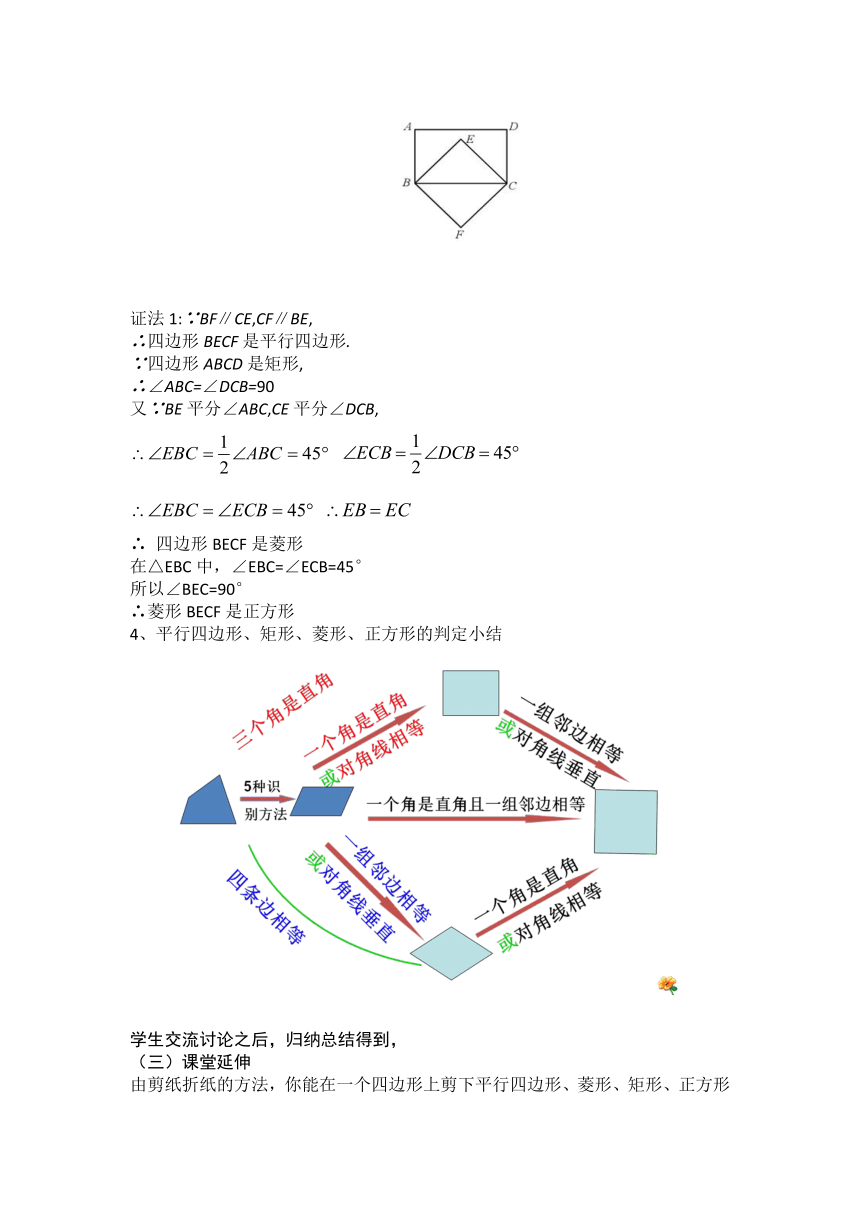
已知:如图所示,在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,BF∥CE,CF∥BE.求证:四边形BECF是正方形.
解析
思路1:要证四边形BECF是正方形,可以先证明四边形BECF是菱形,然后证明四边形BECF中有一个角是直角即可;
思路2:要证四边形BECF是正方形,也可以先证明四边形BECF是矩形,然后证明四边形BECF中有一组邻边相等即可. 试着写一写吧
证法1:∵BF∥CE,CF∥BE,
∴四边形BECF是平行四边形.
∵四边形ABCD是矩形,
∴∠ABC=∠DCB=90
又∵BE平分∠ABC,CE平分∠DCB,
∴ 四边形BECF是菱形
在△EBC中,∠EBC=∠ECB=45°
所以∠BEC=90°
∴菱形BECF是正方形
4、平行四边形、矩形、菱形、正方形的判定小结
学生交流讨论之后,归纳总结得到,
(三)课堂延伸
由剪纸折纸的方法,你能在一个四边形上剪下平行四边形、菱形、矩形、正方形吗?
中点四边形: 连接一个四边形各边中点所得四边形称之为中点四边形
问题:中点四边形形状由什么因素决定呢?
探究活动
方法: 1、特殊化
如果四边形ABCD为特殊的四边形,中点四边形EFGH会是什么样的形状呢?
原四边形可以是( )、( )、( )、( )( )
猜想验证
特殊四边形的中点四边形
平行四边形的中点四边形是:
矩形的中点四边形是:
菱形的中点四边形是:
正方形的中点四边形是:
学生不难得出平行四边形的中点四边形形状,进而得出矩形、菱形、正方形的中点四边形形状,再拓展到一般四边形的中点四边形形状,进一步发展了学生的推理能力。
方法: 2、拓展延伸
对角线相等的四边形的中点四边形是( )
对角线垂直的四边形的中点四边形是( )
对角线既相等又垂直的四边形的中点四边形是( )
对角线既不相等又不垂直的四边形的中点四边形是( )
方法: 3、归纳总结
决定中点四边形EFGH的形状的主要因素是原四边形ABCD的( )
原四边形对角线关系 不相等、不垂直 相等 垂直 相等且垂直
所得中点四边形形状
(四)检测反馈
1.下列说法中正确的有 ( )
①有一个角为直角的菱形是正方形;
②四个角相等的四边形是正方形;
③四条边都相等的四边形是正方形;
④有一组邻边相等的矩形是正方形;
⑤对角线垂直且相等的四边形是正方形;
⑥对角线相等的菱形是正方形;
⑦对角线互相垂直的矩形是正方形;
⑧对角线互相垂直平分的四边形是正方形.
A.3个 B.4个 C.5个 D.6个
2.如图所示,在△ABC中,AB=AC,D,E,F分别是BC,AB,AC的中点,连接DE,DF.
(1)求证DE=DF.
(2)你能添加一个条件,使四边形EDFA是正方形吗 若能,请说明.
目的:对学生当堂所学进行检测,了解学生的接受情况,课后针对不足进行补充练习。
(五)课堂小结
1、本节课我们学习了什么?
可由学生来回答
你有什么收获?说出来与大家分享。
对学生的表现进行表扬和鼓励, 让学生真正喜欢数学
教学目标
探索并证明正方形的判定定理,进一步发展推理能力,
体会探索与证明过程中所蕴含的抽象、推理等数学思想
教学重点:探索并证明正方形的判定定理;
教学难点:综合应用菱形、矩形、正方形的性质定理和判定定理
教学过程
回顾与思考
问题1 什么样的四边形是正方形 正方形有哪些性质?.写下来
投影:1、定义:有一个角是直角且有一组邻边相等的平行四边形
2、性质 边:四边都相等,对边平行
角:四个角都是直角
对角线:相等、垂直且互相平分
对称性:中心对称、轴对称图形
(二) 新课探究
1、问题2 你认为怎样判定一个四边形是正方形?
如图所示,将一张长方形纸对折两次,然后剪下一个角,打开.怎样剪才能剪出一个正方形 动手做一做
(活动目的:通过活动,引入正方形的判定问题)
投影:
2、问题3 议一议:满足什么条件的菱形是正方形 满足什么条件的矩形是正方形 与同伴交流一下.写下来
(目的:引导学生讨论正方形的判定方法,形成判定正方形的基本思路:一个四边形既是矩形又是菱形,这个四边形就是正方形。)
3、例题讲解
已知:如图所示,在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,BF∥CE,CF∥BE.求证:四边形BECF是正方形.
解析
思路1:要证四边形BECF是正方形,可以先证明四边形BECF是菱形,然后证明四边形BECF中有一个角是直角即可;
思路2:要证四边形BECF是正方形,也可以先证明四边形BECF是矩形,然后证明四边形BECF中有一组邻边相等即可. 试着写一写吧
证法1:∵BF∥CE,CF∥BE,
∴四边形BECF是平行四边形.
∵四边形ABCD是矩形,
∴∠ABC=∠DCB=90
又∵BE平分∠ABC,CE平分∠DCB,
∴ 四边形BECF是菱形
在△EBC中,∠EBC=∠ECB=45°
所以∠BEC=90°
∴菱形BECF是正方形
4、平行四边形、矩形、菱形、正方形的判定小结
学生交流讨论之后,归纳总结得到,
(三)课堂延伸
由剪纸折纸的方法,你能在一个四边形上剪下平行四边形、菱形、矩形、正方形吗?
中点四边形: 连接一个四边形各边中点所得四边形称之为中点四边形
问题:中点四边形形状由什么因素决定呢?
探究活动
方法: 1、特殊化
如果四边形ABCD为特殊的四边形,中点四边形EFGH会是什么样的形状呢?
原四边形可以是( )、( )、( )、( )( )
猜想验证
特殊四边形的中点四边形
平行四边形的中点四边形是:
矩形的中点四边形是:
菱形的中点四边形是:
正方形的中点四边形是:
学生不难得出平行四边形的中点四边形形状,进而得出矩形、菱形、正方形的中点四边形形状,再拓展到一般四边形的中点四边形形状,进一步发展了学生的推理能力。
方法: 2、拓展延伸
对角线相等的四边形的中点四边形是( )
对角线垂直的四边形的中点四边形是( )
对角线既相等又垂直的四边形的中点四边形是( )
对角线既不相等又不垂直的四边形的中点四边形是( )
方法: 3、归纳总结
决定中点四边形EFGH的形状的主要因素是原四边形ABCD的( )
原四边形对角线关系 不相等、不垂直 相等 垂直 相等且垂直
所得中点四边形形状
(四)检测反馈
1.下列说法中正确的有 ( )
①有一个角为直角的菱形是正方形;
②四个角相等的四边形是正方形;
③四条边都相等的四边形是正方形;
④有一组邻边相等的矩形是正方形;
⑤对角线垂直且相等的四边形是正方形;
⑥对角线相等的菱形是正方形;
⑦对角线互相垂直的矩形是正方形;
⑧对角线互相垂直平分的四边形是正方形.
A.3个 B.4个 C.5个 D.6个
2.如图所示,在△ABC中,AB=AC,D,E,F分别是BC,AB,AC的中点,连接DE,DF.
(1)求证DE=DF.
(2)你能添加一个条件,使四边形EDFA是正方形吗 若能,请说明.
目的:对学生当堂所学进行检测,了解学生的接受情况,课后针对不足进行补充练习。
(五)课堂小结
1、本节课我们学习了什么?
可由学生来回答
你有什么收获?说出来与大家分享。
对学生的表现进行表扬和鼓励, 让学生真正喜欢数学
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
